基于刚体力学的“同心鼓”协作策略研究
王 何 周俊杰 李泉兵
(1、重庆理工大学 电气与电子工程学院,重庆400054 2、重庆理工大学 理学院,重庆400054 3、重庆理工大学 计算机科学学院,重庆400054)
1 背景介绍
“同心鼓”又名“击鼓颠球”,是一项对团队合作能力要求较高的新兴素质拓展项目,该活动需要在保证安全的情况下,使颠球次数最多。项目开始时,球从鼓面中心上方竖直落下,队员同心协力将球颠起,使其有节奏地在鼓面上跳动,颠球过程中,队员只能抓握绳子的末端,不能接触鼓或绳子的其他位置。该项目在培养团体意识、团队合作能力、进取精神上都有一定积极作用。
2 问题
所用排球质量为0.27kg,鼓面直径为40cm,鼓身高度为22 cm,鼓的质量为3.6kg,参与该项目的人数不少于8 人,队员之间的最小距离不小于60cm。开始时,球从鼓面中心上方40cm 处竖直落下,球被颠起的高度应离开鼓面40cm 以上,如果低于40cm,则项目停止,项目的目标是使得连续颠球的次数尽可能多。根据上述基本要求,建立数学模型解决以下问题:
问题1:在参与人员都能精确控制施力方向、时机和力度的理想状态下,讨论团队的最佳协作策略,给出该策略下的颠球高度。
问题2:在队员不能精确控制发力时机和力度的实际情况下,建立描述队员的发力时机和力度与某一特定时刻的鼓面倾斜角度的关系模型。在队员人数为8,绳长为1.7m,鼓面初始时刻水平静止,初始位置较绳子水平下降11cm 时,求解表1 中0.1s 时鼓面的倾斜角度。
问题3:在实际情况下,根据问题2 模型,调整问题1 的策略。
问题4:在队员人数为10,绳长2m,球反弹高度60cm,球相对竖直方向倾斜1 度,倾斜方向在水平面的投影指向某两位队员之间,且与这两位队员的夹角之比为1:2 时,调整队员拉绳策略,使球能竖直弹跳,求解精确控制条件下所有队员的发力时机及力度,并分析该调整策略的实施效果。
3 模型假设
假设所有参与人员给绳的力为恒力,且施力方向沿绳向外;假设所有参与人员握绳高度相同,绳端处于同一水平面;不考虑绳的弹性势能;不考虑空气阻力对球与鼓运动的影响;所有参与人员之间的距离相等、均匀分布;假设球与鼓总是在鼓上升到最大速度时碰撞。
4 问题分析
问题1:该问为优化问题,将力度作为优化目标。在假设条件下,建立二维直角坐标系。该运动具有循环性,只考虑球从鼓面中心上方40cm、鼓从最低处开始运动到球与鼓再次回到各自原点的单次运动过程,将球与鼓的运动分为鼓上升、球与鼓碰撞、恢复原状态三阶段,对球与鼓每一阶段的运动进行分析,从而建立优化模型求得最优力度。
问题2:从单力不平衡、多力不平衡、单人提前发力、多人提前发力、提前发力与多力不平衡五种情况分析发力时机和力度与鼓面倾斜角度的关系。
问题3:现实情况下,所有参与人员不可能对发力时机与力度进行精确控制,根据颠球间隔和人的正常反应时间对问题1中的策略进行调整。
问题4:球运动方向不再竖直,小球相对于竖直方向产生1°的倾斜角度,以鼓为中心建立直角坐标系,假定鼓的倾斜方向在队员1 与队员2 之间,且与 轴正半轴右夹12°。可以设在该方向上增加△F,由此对鼓产生新力矩,在球与鼓碰撞前,转动鼓面使其恢复水平状态,将△F 分解在队员1 与队员2 上,即△F1和△F2,即可使鼓变为水平状态。
5 模型建立与解决
5.1 问题1:模型建立和求解
5.1.1 模型的建立
将力度作为优化目标,将球与鼓的运动分为鼓上升、球与鼓碰撞、恢复原状态三阶段,对球与鼓每一阶段的运动进行分析,如图1 所示。
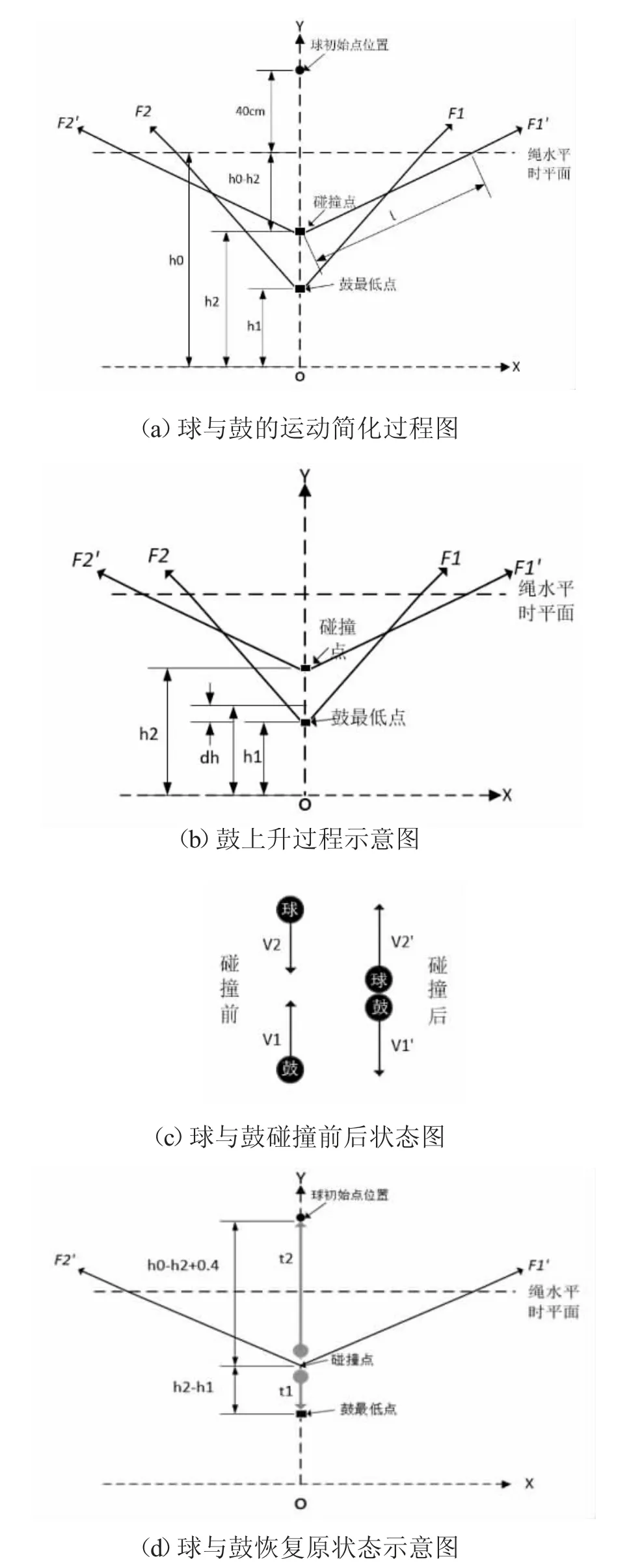
图1


5.1.2 模型求解
利用Matlab 求解得到不同绳长l、绳水平时所处水平面离地面的高度h0以及参与人数n 等参数条件下的策略,为了更好的描述以上三个参数对优化目标的影响,分别给出不同参数下的施力情况。
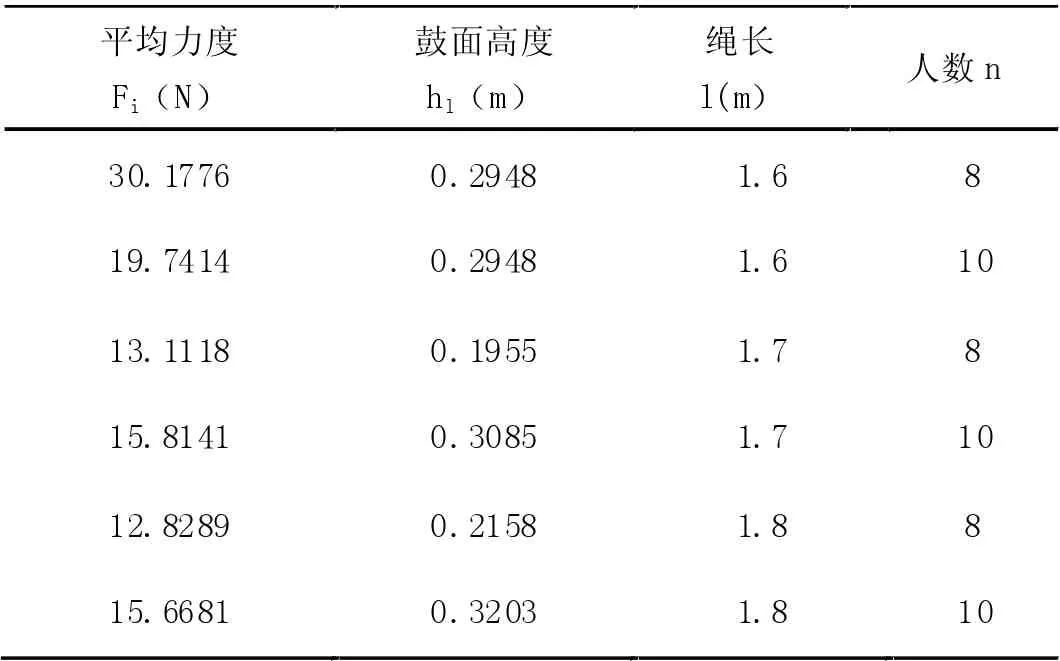
表1 不同参数条件下的策略解
5.2 问题2:模型建立与求解
对题目中的八种情况,分为5 种不同情况进行求解。
5.2.1 单力不平衡


5.3 模型结果
根据以上几种模型对具体实例样本进行求解,求解结果如表2 所示。

表2 样本的鼓面倾斜
6 问题3:最优策略模型的调整
在理想情况下建立的模型忽略了空气阻力、碰撞点的能量损失、碰撞后鼓的速度以及恢复系数的准确性。根据实际情况,给出三种模型调整策略。
6.1 增大小球碰撞前后的速度v2、v2'
增大碰撞前后的小球速度,从而增大小球上升与下落的时间,使参与人员拥有足够反应时间做出相应调整,进而对球进行更好的控制。
6.2 调整施力大小
STEP1:确定球从最初位置下降到返回原位置的总时间及小球碰撞前的速度v2。
STEP2:确定样本中鼓的倾斜角度。
STEP3:确定调整力的合力矩。
STEP4:计算鼓角加速度。
STEP5:确定 β表达式。
STEP6:分解调整力。
STEP7:求解调整力。
通过上述步骤可得样本1 中第5 号成员的调整力为92.03N,且球来回弹起的时间在人正常反应时间内。根据以上分析可知,若需在短时间内调整鼓面,则需更大的调整力,当球来回运动的时间较长时,可用较小的力使鼓面恢复水平。
6.3 所有参与人员用力拉绳,将绳绷紧
若有参与人员提前发力或发力不均时,其他成员能尽快感知并及时做出调整,便能及时控制鼓面倾斜,保证球始终落在球面上且尽量保持竖直运动。
7 问题4:精确控制条件下调整球为竖直弹跳的策略
7.1 调整策略



图2 三维坐标系

7.2 调整策略效果分析

由于2 中为理想情况,且绳长取值在1 米左右,而在第四问中绳长为2 米,这导致两种情况下的h1差距较大,其余参数取值差异不大,则可以认为问题四的调整策略在现实情况中实施效果较好。

