生长激素内分泌调节的模型及混沌行为研究
巴合提古丽·阿斯里别克,张文雅,吐尔逊·艾迪力比克,孙迎春
(1.伊犁师范大学电子与信息工程学院光电材料与器件实验室,新疆 伊宁 835000;2.中国人民解放军联勤保障部队第九六四医院,吉林 长春 130062;3.东北师范大学物理学院,吉林 长春 130024)
0 引言
生长激素(growth hormone,GH)是人体生长发育的重要因素之一,它在体内的分泌释放受多重因子的调节,但直接的来源是腺垂体生长激素细胞.诺贝尔医学奖获得者John Gurdon指出,人体身高由核心轴生长轴及合成代谢轴、生长神经轴、内分泌轴、下丘脑垂体轴、长骨生长轴等相关因素决定,能有效解决增高的方法只有“生长轴重组体系”[1].可见,生长激素在促进人体的生长发育中是起极其重要的作用.从组织和分子水平上说,生长激素促进了构成各种组织的分子及蛋白质的合成,促进骨及骨关节等的生成[2-3].研究人员很早就发现,人幼年期如GH分泌不足,会出现生长停滞、个子矮小的现象,严重者会出现侏儒症等病症;GH分泌过多,则会导致生长过快,甚至出现巨人症和肢端肥大症等[4-6].
生长激素及其相关调节因子的作用在生理学上已很明确,其调节循环主要依赖于神经内分泌生长系统,在生长发育的相关理论中称之为神经内分泌生长轴,简称生长轴.该系统主要是由下丘脑、垂体、靶腺的一系列激素及受体构成[7].系统内激素的分泌具有明显的节律性,比如:青春前期和青春期的青少年24 h内生长激素脉冲数6~8次,平均3~4次,并具有夜间分泌量及频率都比白天多的规律,在深睡后1 h左右,生长激素分泌最旺盛,可达50~60 μg/L[8],因此,想长高的孩子要保证充足且高质量的睡眠.此外,其在血液中浓度还有1~3 h脉冲式释放的节律[9-10],这种具有节律的现象在地球上是普遍存在的,最典型的例子之一就是昼夜节律及伴随而来周期性的觉醒与睡眠.实际上,太阳、月亮的运动规律直接导致了地球上生物的节律性变化,违反这种自然的节律会引起人的机体功能混乱、情绪烦躁、工作效率降低等现象[11-12].有关生物节律的研究早已成为了许多学科领域的研究热点[13-15],尤其是分子水平发现的节律控制机制,揭开了生物节律的奥秘,得到了科学界的普遍认可[16-19].
目前,非线性科学在各个领域得到了广泛的应用[20-22],比如在神经网络系统、保密系统、生命科学等方面的应用都获得了很好的效果,已成为新的研究热点[23-27].因此,本文采用非线性的理论和方法,结合生理学和酶促反应动力学等理论,对人体生长系统中的激素分泌进行建模研究,从而揭示生长激素内分泌调节的行为和规律.
1 模型的构建
1.1 生长激素内分泌调节机制及简化框图
下丘脑-垂体-靶细胞轴的作用主要是通过控制人体各个靶器官激素的分泌,来调节人体的生长发育等功能.其分泌的激素主要包括生长激素、糖皮质激素、甲状腺素、性腺激素等.神经内分泌生长轴是其中的一个分支,它有刺激和抑制两方面的通路.它的刺激生成路径:首先由下丘脑中的神经元分泌生长激素释放激素(Growth Hormone Releasing Hormone,GHRH),然后,GHRH与其受体结合,促进了垂体释放出GH激素,GH又刺激肝脏等外周器官和组织来分泌类胰岛素生长因子(Insulin-like Growth,IGFs),并借助IGFs实现对机体生长发育的调控作用.它的反馈循环路径主要有两方面:一是血液中过高浓度的GH通过垂体门脉血管逆流,激发了生长激素释放抑制激素(Growth Hormone-releasing Inhibitory Hormone,GHIH)的分泌,这直接对GHRH的分泌起到了抑制作用,即为负反馈,也称之为短环反馈(short-loop feedback);二是血液中的IGFs也间接抑制GHRH的生成,从而抑制了垂体细胞分泌GH.实验表明,IGFs可在下丘脑和垂体两个层面以负反馈机制来调节GH的分泌,由于GH分泌受控,反过来又影响了IGFs自身的分泌,这种反馈也称之为长环反馈(long-loop feedback)[28-31].生长激素具有促进生长发育,影响糖、蛋白质、脂肪代谢的生理作用.通常运动、睡眠等外在因素,对GH的分泌也有一定影响,但其自发性分泌是始终存在的.正常情况下,GH的分泌具有昼夜节律性,且呈脉冲式.综合以上分析,在忽略次要影响因素的情况下,可将生长轴系统各因素之间的正负反馈作用见图1.

图1 下丘脑-垂体-生长轴中各激素正负反馈模拟图
1.2 神经内分泌生长轴激素分泌动力学模型
神经内分泌生长轴系统中,激素之间相互作用不是简单的线性关系.已有的知识只停留在定性表示系统内部的调控是通过激素之间的相互协调完成的层面上,但缺少表示这些变量之间确切依赖和联动关系的动力学分析.激素分泌随时间变化的非线性动力学分析可解决以上问题,能全面展现此系统激素分泌的昼夜节律和激素间相互调控的精确依赖关系.
从分子水平上看,生物的生长发育及新陈代谢等都是酶催化下的酶促反应,因此符合酶促反应动力学理论[32].利用Michaelis-Menten定律及其推广形式[33],则体内激素的生成速率以分数形式成立,将生长轴内外周血中激素的浓度设为变量,即可建立此变量随时间变化的微分方程组:
(1a)
(1b)
(1c)
式中:x1表示下丘脑神经元分泌的GHRH的血浆浓度(单位:μg/L);x2表示腺垂体分泌的RH的血浆浓度(单位:μg/L);x3表示肝脏等靶器官分泌的IGFs的血浆浓度(单位:μg/L);t表示时间(单位:min);λi表示机体对各个激素的代谢清除系数(Metabolic Clearance Rate,MCR),是激素的自然代谢过程;ai(i=1,…,14)为正的常系数,其中:a2表示下丘脑神经元自主分泌(Autonomous Secretion)的激素,a1,a6,a12表示对应器官以外的激素分泌强度,比如,a1是下丘脑以外的释放激素分泌源的分泌强度,也包括神经系统对生长激素释放激素分泌的影响,其余的常系数表示激素间的相对作用强度.
在方程组(1)中,分子中出现的变量表示对自身的分泌有促进作用;分母中出现的变量则表示对自身的分泌起负反馈作用;当变量同时出现在分母与分子中时,则表示此激素自身具有饱和性.以方程(1a)为例,GHRH分泌过程呈现分数形式,表示出是复杂的酶促反应过程,分子中的x1表示GHRH对自身的分泌起刺激作用,分母中的变量x2和x3分别表示GH和IGFs对GHRH起着负反馈作用.依此类推,即构建出了神经内分泌生长轴激素分泌的非线性动力学方程.
方程组中表示的是各变量xi随时间变化的动力学演化规律,由于其中分式的分母或分子的所有系数均为正,基于代数方程的理论可知,该方程组没有实数的解析解,而xi表示激素在血液中的浓度,且都为正值,即实际模型分式的分子无极点,分母无奇点[34],模型中分式不存在奇点发散的情形.分式具有非线性特征,它与清除项的共同作用,可以维持系统处于振荡周期或混沌状态.
2 模型方程组的求解与分析
为了求解方程组(1)中的17个待定常数,只能采取给予这些常数赋值后进行运算的试探法,即通过反复多次的试探和迭代去寻找合理的常系数.因此采用Matlab计算平台,针对方程组(1)式进行编程和计算,从而获得神经内分泌生长轴非线性动力学模型的数值解.
2.1 模型方程的周期振荡解
首先依据临床上实际测定的数据[35-36],选取x1,x2,x3适当的初始条件(分别为0.1,1.2,220 μg/L),在Matlab软件中运用变步长四阶龙格-库塔法,并赋予模型方程组中的待定常系数为如下数值时,就获得了神经内分泌生长轴激素分泌具有周期振荡的行为方程组为:

(2a)
(2b)
(2c)
模拟出的这组周期振荡解的时域图见图2.从图2中可以看出,x1,x2,x3的分泌随时间都以均匀振荡的形式出现,周期均为199.05 min,相应的振荡峰值分别为0.33,1,248 μg/L,均在临床测得值范围之内[35-36].已有实验证明[37]:GH的释放呈脉冲式分泌状态,每隔1~4 h出现一个脉冲,其脉冲式分泌正是由于GHRH的脉冲式分泌而决定的,GHRH无论在白天或夜晚成长激素皆呈脉冲式释放,间隔3~5 h,脉冲期间的基础值很低.从图2明显可见,各个激素的浓度呈周期性变化,说明激素的分泌的节律性,其振荡幅值和周期大小均与实验结果一致[35-36].

图2 各个激素浓度随时间演化的时域图
为了进一步分析激素间分泌的递进关系,通过运算将时域图变换为激素间相互作用的相图表示(见图3).

(a)GHRH-GH;(b)GH-IGFs
由图3可见,在经过初始暂态后,各激素相互关系形成了一个封闭的曲线,形成了一个循环的动力学过程.图3(a)显示,同一个x2值对应闭合曲线上的一大一小2个x1值,说明了系统中激素间分泌的正负反馈关系,处在正向进程中时,随着x1的增加,x2也呈现增加状态,但到达峰值后,则出现了负反馈进程,x2对x1的负反馈,使得x1分泌减少,进而又影响了x2的分泌,二者都呈现分泌下降的状态.图3(b)显示,首先是x2和x3同时呈现增大状态,达到峰值后,x2开始下降,但此时x3还在继续增加,当x2下降到0.321 μg/L时,x3才开始下降,二者的正负反馈调节是有延迟的.
2.2 激素特征量的理论计算
2.2.1 各激素基础值

(3)

2.2.2 激素的代谢清除率MCR
方程组(1)中的λi表示激素的代谢清除系数,因此,MCR可写成
MCRi=Viλi.
(4)
其中Vi是激素的分布体积,临床上还很难准确给出它的准确值,但通常得到认可的是把Vi认定为人体的外周血的体积[38-39].不同的实验和分析方法总是给出不同的Vi值,因此,使用文献[38-40]的参数,即V1=V2=V3=5 L.这样,由方程(4)可算得MCRi为:
MCR1=V1λ1=5×0.059 L/min=2.95 L/min=424.8 L/d;
MCR2=V2λ2=3.8×0.023 5 L/min=0.494 L/min=128.6 L/d;
MCR3=V3λ3=5×0.006 L/min=0.025 5 L/min=43.2 L/d.
2.2.3 激素的产生率
激素的产生率(Production Rate)即为单位时间内激素产生出的量值,应等于(2)式中的前
两项取平均值再乘以各自的分布体积Vi来求得.因此,3种激素的产生率P分别为:

当V1=V2=V3=5 L时,分别可得到各激素产生率为:
P1=1.37×10-3μg/min=1.974 μg/d;
P2=5×10-3μg/min=7.2 μg/d;
P3=5.08 μg/min=7.32 μg/d.
2.2.4 激素半衰期
激素半衰期(用τi表示)可表示激素更新的速度,其与代谢清除有关,计算公式为
(5)
因λi(i=1,2,3)已算得,分别为0.058,0.023 5,0.006,因此
τ1=ln2/0.058=11.95 min;
τ2=ln2/0.023 5=29.5 min;
τ3=ln2/0.006=115.5 min.
可见,GHRH、GH、IGFs的半衰期逐渐增加,GHRH最短,说明其在下丘脑中生成后存在的时间最短,而IGFs最长,说明在外周器官中存在时间最长,接近2 h.
为了进一步检验理论模型的合理性,将理论计算值与实际临床检测值[33-36]进行一一对比(见表1),发现激素的各个特征量都符合得很好,说明建立的理论模型是合理的.

表1 激素特征量的临床测得值和理论计算值对比
3 激素的非线性分泌过程
3.1 模型方程的倍周期解
非线性系统的一种极为重要的运动形态就是混沌行为.地球上的各种生物是自然界最复杂的系统,在其各种运动变化中出现混沌状态已被大量的事实和分析所证明[40].因此,神经生长轴内分泌调节的过程也不能是严格的周期行为,而应该是在限定范围内具有一定变动的混沌行为.为了验证这一点,对建立的模型做进一步的赋值计算,首先在基础值附近选取初值,分别为:x10=0.007 μg/L,x20=0.04 μg/L,x30=7.5 μg/L,然后进行反复迭代,则在周期振荡解的基础上,得到了具有倍周期特征的解,即方程组为:

(6a)
(6b)
(6c)
求出方程组(6)数值解的时域图(见图4),可见激素浓度经过短暂的暂态过程之后呈现出非周期振荡状态,与周期振荡解类似,在1 000 min内,仍然具有5个激素分泌的峰值,之后再进行如此的循环,呈现出明显一高一低的2倍周期变化特征.

图4 各激素2倍周期分泌的时域图
为进一步清楚显示激素间的相互作用关系,做出2倍周期解的相图表示见图5.由图5可见,经过一个暂态后,系统进入一大一小2圈的循环状态,这2圈一直持续循环不重合,表明了系统从周期振荡进入了倍周期的分叉过程.

(a)GHRH-GH;(b)GH-IGFs
3.2 模型方程的混沌解
通过计算发现,初始迭代时,系统一般有个暂态过程,但当迭代次数很大时,随时间的演化会导致一个确定的、对初值极为敏感的终态.终态可取无穷多个值,当a1在(7.5~9.2)×10-5之间变化时,方程组(6)的解是倍周期的,但当a1大于9.2×10-5时,系统就出现了多值状态,是从周期分叉后进入混沌状态的一种方式,是一条典型的通向混沌的道路.此时模型方程组为:

(7a)
(7b)
(7c)
求出其数值解的时域图见图6,由图6可见,系统处于的是非周期振荡状态,各激素随时间的分泌量不呈现规律的周期性,分泌峰值的大小不一致,每次到达峰值的时间间隔也不相同,但所有的峰值都限定在一个范围中,不会无限变化,且与周期振荡类似,在1 000 min内有5个峰值,呈现出典型的混沌行为.
为进一步展现混沌状态的特征,做出系统方程组的相图表达(见图7).由图7可见,系统经暂态后进入了多循环中,其运动轨迹被限定在相平面的有限区域内,呈现出密集的循环带,这也是混沌的典型特征之一.
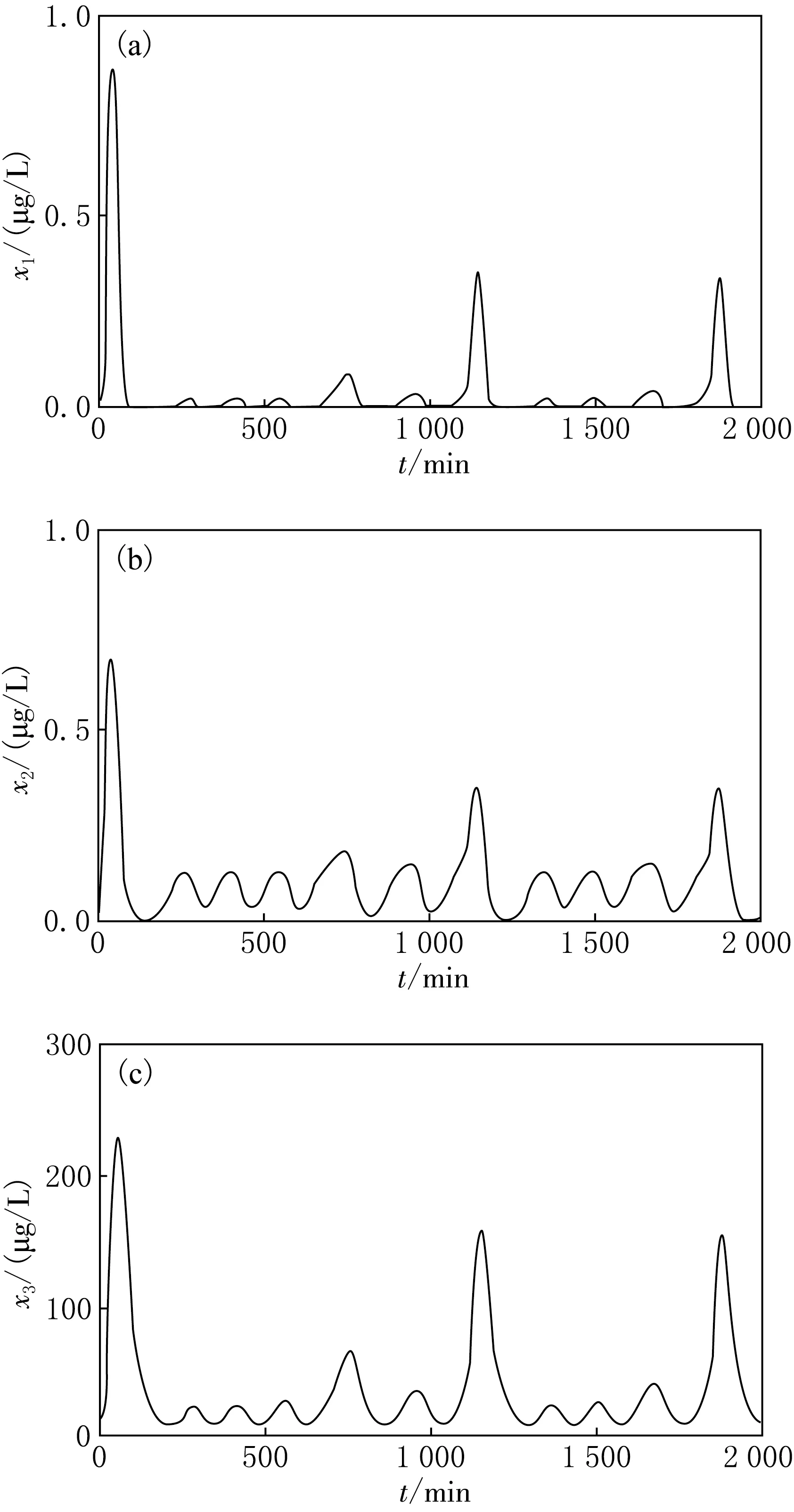
图6 各激素混沌状态的时域图
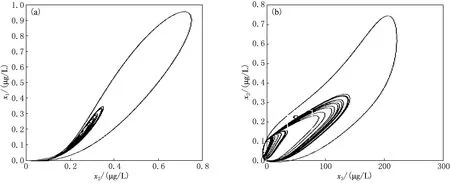
(a)GHRH-GH;(b)GH-IGFs
生长激素内分泌调节的模型及混沌行为研究表明,神经内分泌生长轴内激素分泌的正负反馈调节,使系统呈现出了典型的混沌状态,而混沌态的存在,则表示生长激素内分泌调节一定服从非线性规律.

