基于组合模型的三角模糊数预测模型

谢小军,马 虹，乔希民

基于组合模型的三角模糊数预测模型

*谢小军1,马 虹2，乔希民1

( 1.广州工商学院，广东，广州 510850；2.广东金融学院，广东，广州 510521)

首先以北京市1994-2006年年平均最低气温、年平均气温、年平均最高气温构建三角模糊数序列的三个界点，出于数据整体性考虑将三角模糊数序列转换成等量信息的三个指标数序列，然后，对三个指标数序列分别构建了时间序列ARIMA模型，灰色预测GM(1,1)模型以及BP神经网络模型，最后在单一模型预测结果的基础上通过引入诱导有序加权（IOWA）算子，建立了一种集成IOWA算子的ARIMA-GM- BP的三角模糊组合预测模型。通过最终预测结果对比，组合模型预测精度明显要高于各单一模型。

ARIMA模型；GM(1,1)模型；BP神经网络模型；IOWA算子；组合预测模型

0 引言

自从1969年Bates和Grange提出了组合预测方法后[1]，越来越多的学者关注组合模型，并开展了大量的研究。最初利用组合模型研究的对象大多数是实数，但随着社会经济的不断发展，系统的复杂性与事物的不确定性不断提高，导致事物更具模糊特征，很多时候是以区间数或者三角模糊数的形式表示，例如很多经济指数可以用区间数来表示，利用最小值和最大值来构造区间数的两个界点[2]，还有温度可以用一个三角模糊数来表示，最低和最高温度可以表示三角模糊数的左端点和右端点，平均温度表示其中点。研究三角模糊数组合预测模型既具有理论意义也具有现实意义。在模糊环境下，三角模糊数是刻画事物的一种常见的不确定信息的表达形式，它弥补了实数和区间数的不足。另一方面，三角模糊数可以利用其隶属函数更好地描述事物的特征。目前针对三角模糊数为研究对象的预测方法文献相对较少，主要分为：1）直接以三角模糊数的三个界点建立预测模型或者利用成熟的单一模型[3-4]。直接对三角模糊数的三个界点进行建模和预测，其存在的缺陷是：a.不能很好地描述序列整体性的发展趋势；b.建立的模型所预测的结果容易发生错乱，导致预测失效。2）将区间数转换为对称三角模糊数[5-6]，并利用提出的组合模型进行预测，但是对于一般三角模糊数并没有提出行之有效的方法。因此，提出能够降低一般三角模糊数的预测误差有效组合模型具有重要的理论意义与实际价值。

近几年组合预测方法的研究比较热门[7-12]，特别是将组合模型运用到区间数的研究比较多。例如文献[8]引进诱导有序加权平均(IOWA)算子构建了凸组合为准则的区间组合预测模型。文献[9] 根据联系数与区间数的性质将区间数转换为联系数的表示形式,结合诱导有序加权调和平均算子与向量夹角余弦，建立了联系数型区间组合预测最优化模型。文献[10]提出一种最优权重系数的三角模糊数的组合预测新方法，构建了基于诱导连续有序模糊加权平均（ICOFWA）算子的模糊连续区间变权组合预测模型。文献[11]以灰色趋势关联度为相关性指标，提出了基于灰色趋势关联度的诱导有序加权的连续区间广义有序加权调和平均算子的区间数组合预测模型。文献[12]将COWG-WPA算子应用于区间型组合预测问题中,在广义绝对误差λ次和的准则下建立了基于连续区间有序几何加权平均Power算子的区间型组合预测模型。

大多数组合模型是直接将各单项模型加权平均，因此，组合模型的关键是如何确定各单一模型的权系数。本文通过结合IOWA算子，建立一种基于ARIMA-GM-BP的三角模糊数最优权系数组合预测模型，通过数据实验表明了该方法的可行性和有效性，与单一方法对比，预测精度都有明显提高。

1 基本概念

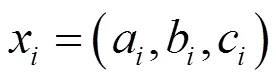
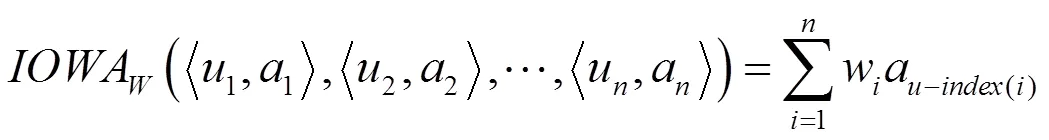
2 三角模糊数序列的构建和转换

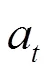
表1 转换后原始数据及各单项预测方法拟合预测值

Table 1 Fitting predicted values of original data and individual prediction methods after conversion

原始数据方法1：ARIMA模型方法2：GM（1，1）模型方法3：BP网模型 19948.913.7195.0913.0613.165.0513.7013.876.1214.2314.31 19958.513.318.75.0713.2013.395.1812.9013.035.1113.5813.50 19968.212.717.95.0812.9113.095.1712.9513.084.8412.6913.91 19977.913.118.54.9712.7412.945.1612.9913.125.3213.8514.32 19988.313.118.45.1313.0313.105.1413.0313.175.9714.1113.74 19997.913.118.65.0913.3313.475.1313.0713.215.3613.8813.92 20007.612.818.35.2113.1613.295.1213.1113.265.3412.8112.91 20017.712.918.25.2812.7512.915.1113.1513.305.5512.9213.89 2002813.218.75.2712.9713.025.1013.1913.355.3713.8813.46 20038.212.9185.3113.1213.255.0813.2313.404.9212.9313.10 20048.913.518.85.1112.9713.095.0713.2813.445.0013.5814.65 20058.513.218.55.0313.1413.335.0613.3213.495.9213.9914.32 20068.913.418.75.0213.0313.175.0513.3613.535.7213.7513.67

3 三角模糊数时间序列ARIMA模型的建立

ARIMA(Auto regressive Moving Average)主要有自回归模型(AR(p))、移动平均模型(MA(q)) 以及自回归移动平均模型(ARIMA(p,q))，其中ARIMA(p,q)模型是AR(p)与MA(q) 的组合，因此也被称之为混合模型。ARIMA模型的通常为：

其中；为平稳可逆ARIMA(p，q)模型的自回归系数多项式，p为移动平均的数目；，p为自回归模型的阶数， 为白噪声序列，B为滞后算子。某一序列经过d阶差分化为平稳序列后建立的ARIMA(p,q)模型称为ARIMA(p,d,q)模型。ARIMA模型建模的基本流程如图1所示。

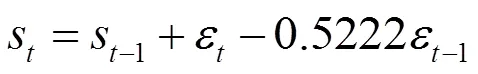
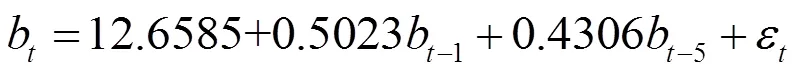
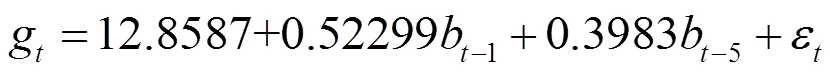
利用上述所构建模型回测得到1994-2006年的拟合预测值见表1。

4 三角模糊数GM(1,1)模型的建立

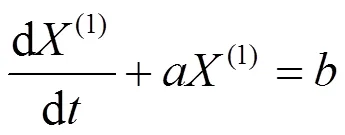
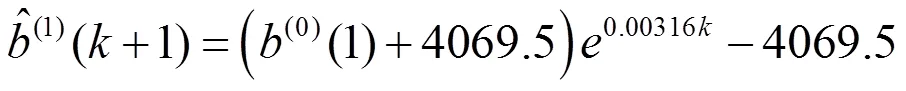
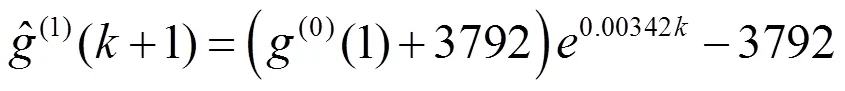
5 三角模糊数BP神经网络模型的建立

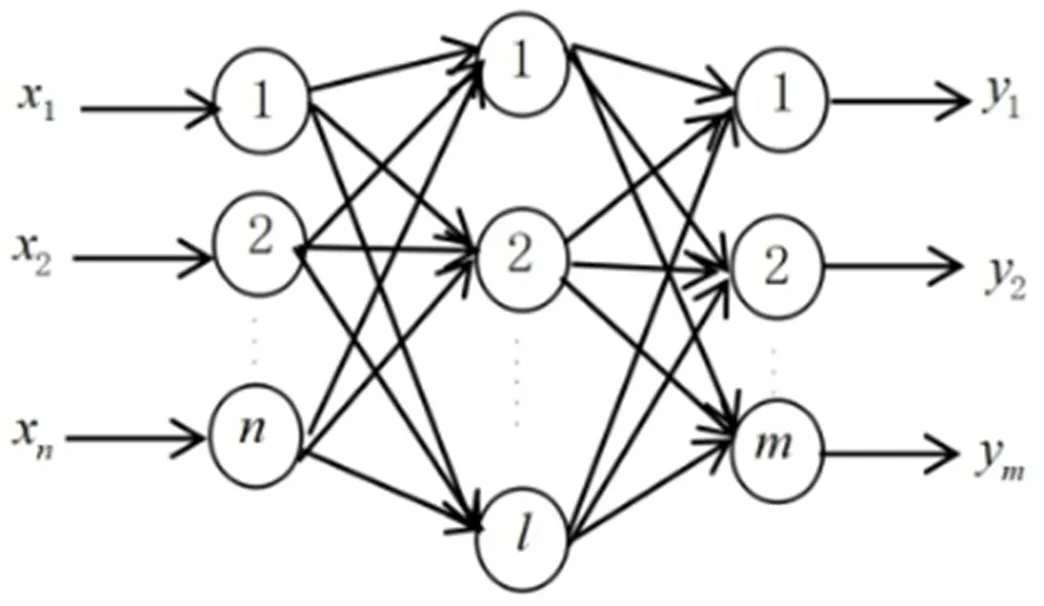
图2 BP神经网络基本结构

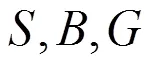
表2 各指标序列构建的BP网络结构

Table 2 BP network structure of each index sequence

序列网络结构：输入层-隐含层-输出层 面积指标序列S2-3-1 中界点指标序列B3-5-1 重心指标序列G3-5-1

6 ARIMA-GM-BP的三角模糊数组合预测模型的建立

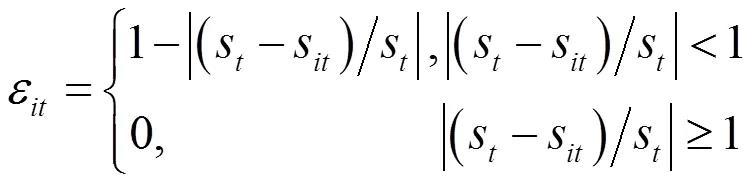
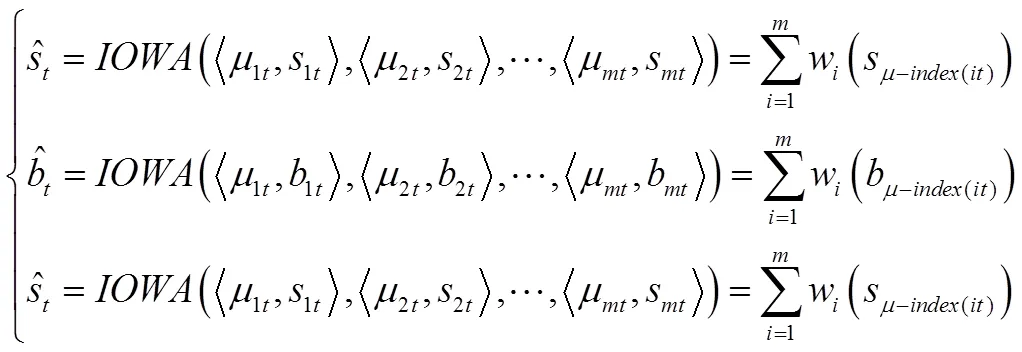
定义4令：

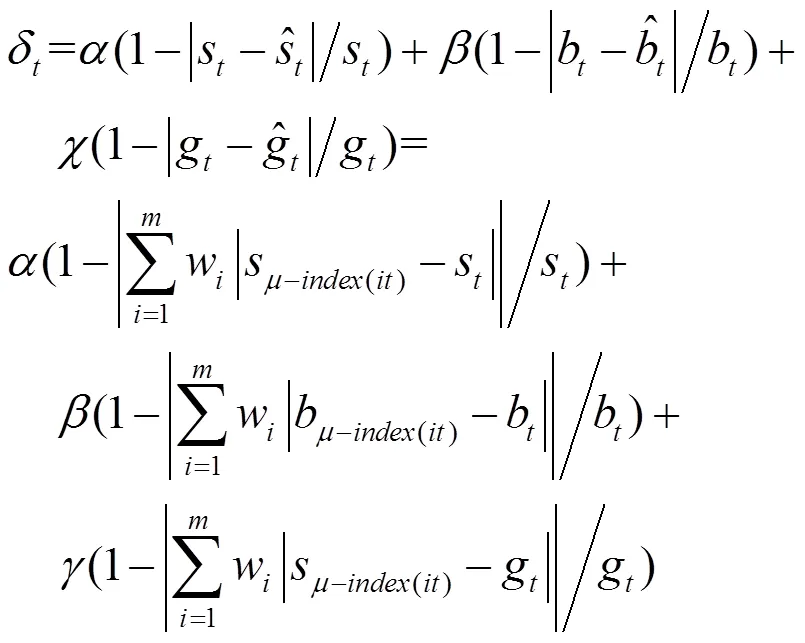
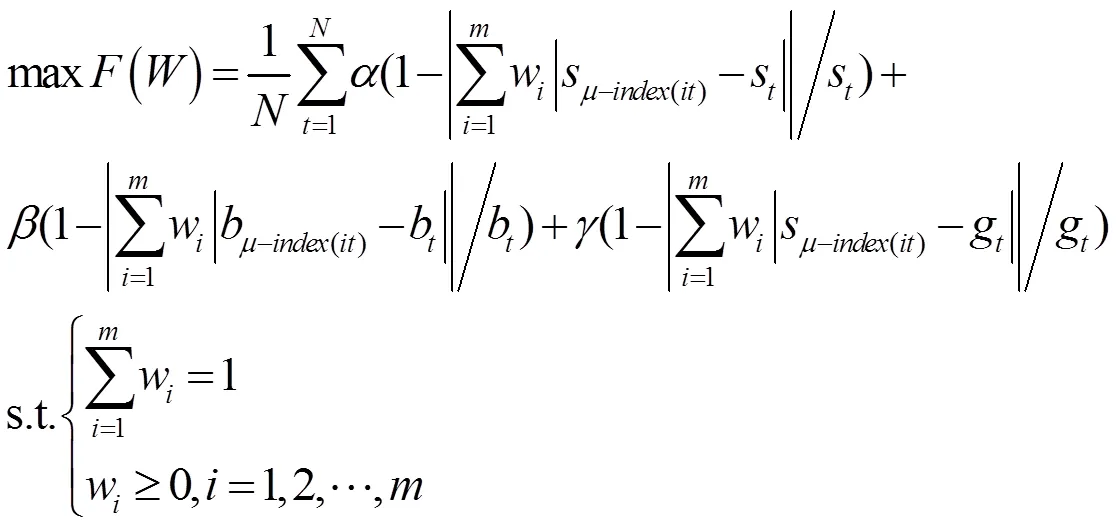
7 有效性实例分析

表3 各参数值对应的组合模型的最优权系数

Table 3 Optimal weight coefficients of the combined model corresponding to each parameter value

本文组合模型权系数α=0.2,β=0.3,γ=0.5α=0.5,β=0.2,γ=0.3α=0.1,β=0.6,γ=0.3 w10.96520.95920.9578 w20.01900.04080.0230 w10.01580.00000.0192

表4 本文组合模型预测值

Table 4 predicted values of the combined model in this paper

原始数据α=0.2,β=0.3,γ=0.5α=0.5,β=0.2,γ=0.3α=0.1,β=0.6,γ=0.3 19945.0513.713.875.0713.7013.875.0513.7213.895.0713.7013.87 19955.113.313.55.1113.2013.495.1113.2213.505.1113.2013.49 19964.8512.712.934.8512.7013.094.8512.7013.084.8512.7013.10 19975.313.113.175.3112.9913.145.3112.9813.125.3113.0013.14 19985.0513.113.275.1413.0413.185.1313.0313.175.1513.0513.18 19995.3513.113.25.3513.0913.235.3513.0813.225.3513.0913.23 20005.3512.812.95.3312.8312.925.3312.8312.925.3312.8312.93 20015.2512.912.935.2812.9212.935.2712.9112.935.2812.9212.94 20025.3513.213.35.3613.2013.355.3713.1813.355.3613.2013.35 20034.912.913.034.9312.9413.114.9312.9413.114.9312.9413.11 20044.9513.513.735.0013.5613.455.0013.5713.435.0013.5613.46 2005513.213.45.0513.1613.355.0413.1513.345.0513.1613.36 20064.913.413.675.0313.3613.665.0213.3813.675.0313.3613.66

表5 本文组合模型与各单项预测方法预测效果评价指标以及预测精度

Table 5 prediction effect evaluation indexes and prediction accuracy of the combined model and individual prediction methods in this

预测模型MSESMSEGMSEMMSEI平均预测精度 单项方法10.05270.08830.09880.23980.9762 单项方法20.04710.06330.07190.18230.9811 单项方法30.14600.14930.18610.48140.9552 组合模型α=0.2,β=0.3,γ=0.50.01400.01410.02710.05520.9952 组合模型α=0.5,β=0.2,γ=0.30.01240.01520.02900.05660.9953 组合模型α=0.1,β=0.6,γ=0.30.01430.01380.02700.05520.9951

8 结语

[1] Bates J M, Granger C W J. The Combination of Forecasts[J]. Journal of the Operational Research Society, 1969,20(4):451-468.

[2] 谢小军,马虹,杨付贵,等. 一种新的区间模糊数时间序列预测模型[J]. 曲阜师范大学学报:自然科学版,2020，46(4):72-76.

[3] 胡丽芳,关欣,邓勇,等. 一种三角模糊数型多属性决策方法[J]. 控制与决策, 2011(12):119-122.

[4] 曾祥艳,舒兰,蒋贵荣,等. 基于三角模糊数序列的灰色预测模型[J]. 数学的实践与认识, 2012(19):109-114.

[5] 袁宏俊,杜康,胡凌云. 基于三角模糊数相似度的区间型组合预测模型[J]. 统计与决策, 2019, 35(6):24-29.

[6] 谢小军,邱云兰,时凌. 基于ARIMA和BP神经网络组合模型的能源消费预测[J]. 数学的实践与认识, 2019(10):292-298.

[7] 谢小军,马虹,杨付贵,等. 基于组合模型的区间模糊数时间序列预测模型[J]. 阜阳师范大学学报:自然科学版, 2020(3):9-13..

[8] 王晓,刘兮,陈华友,等. 基于IOWA算子的区间组合预测方法[J]. 武汉理工大学学报:信息与管理工程版, 2010(2):55-59.

[9] 林义征,袁宏俊,宋马林. 基于IOWHA算子与向量夹角余弦的联系数型区间组合预测[J]. 统计与决策, 2016(5):84-86.

[10] 朱家明,陈华友,周礼刚,等. 基于ICOFWA算子的连续区间模糊组合预测模型及其应用[J]. 模糊系统与数学, 2016(30):184.

[11] 曹晓俊,袁宏俊. 连续区间广义有序加权调和平均算子及其在区间组合预测中应用[J]. 南京理工大学学报:自然科学版, 2017,41(1):124-131.

[12] 袁宏俊,胡凌云. 基于连续区间有序几何加权平均Power算子的区间型组合预测模型[J]. 数理统计与管理, 2019(2):270-280.

[13] 徐泽水. 对方案有偏好的三角模糊数型多属性决策方法研究[J]. 系统工程与电子技术,2002,24(8):9-12.

[14] 尹青,张华,刘洋. 近58年北京气温变化特征分析[C]. 第26届中国气象学会年会气候变化分会场论文集. 2009.

Triangular Fuzzy Number Prediction Models Based on Combination Model

*XIE Xiao-jun1，MA Hong2，QIAO Xi-min1

（1.Guangzhou College of Technology and Business, Guangzhou, Guangdong 510850,China；2.Guangdong University of Finance, Guangzhou, Guangdong 510521,China)

Firstly, the three boundary points of the triangular fuzzy number series were constructed based on the annual mean minimum temperature, annual average temperature and annual average maximum temperature in Beijing from 1994 to 2006. Considering the data integrity, the triangular fuzzy number series was transformed into three index series with equal information. Then, the time series ARIMA model, the Grey Prediction GM (1, 1) model and BP neural network model were constructed respectively for the three index series. Finally, based on the prediction results of a single model, we introduced a weighted triangular fuzzy combination forecasting model with ARIMA-GM- operator and IOWA operator by introducing the induced ordered weighted (IOWA) operator. Through the comparison of the final prediction results, the prediction accuracy of the combined model was obviously higher than that of the single model.

ARIMA model; GM (1,1) model; BP neural network model; IOWA operator; combined forecasting model

F224/O159

A

10.3969/j.issn.1674-8085.2021.02.004

1674-8085(2021)02-0019-07

2020-11-08；

2020-12-13

广东省普通高校青年创新人才项目（2018KQNCX307）；广州工商学院2019年院级科研课题立项项目（KA201933）

*谢小军(1990-)，男，湖南耒阳人，讲师，硕士生，主要从事预测理论与算法研究(E-mail: 454625759@qq.com);

马 虹(1989-)，女，安徽宿州人，助教，硕士生，主要从事决策分析与预测研究(E-mail: 1037496299@qq.com);

乔希民(1960-），男，陕西洛南人，教授，主要从事格上拓扑学与非经典数理逻辑研究(E-mail: 1286181519@qq.com).