基于3RRS-Bricard复合空间捕获系统运动学分析

刘维惠，李晓辉,*，文闻，赵靖超，姚燕安，李锐明

1. 北京控制工程研究所 精密转动和传动机构长寿命技术北京市重点实验室，北京 100094 2. 北京交通大学 机械与电子控制工程学院，北京 100044

随着航天任务的不断拓展，太空环境中残留的大量空间碎片已经对航天事业的发展构成了巨大的威胁[1]。空间非合作目标具有运动状态未知、惯性大和抓捕点不确定等特点[2]，因此，以空间机械臂为主的刚性捕获[3-5]存在较大的碰撞风险。然而，以飞网、飞爪等[6]机构为主的柔性捕获方式难以执行主动消旋和在轨维护等复杂的精细操作任务。因此，研究适应跨尺度、多样化目标并具有主动消旋能力的新型空间捕获系统具有重要意义。

由于可展机构具备展收比大、刚度高、可重复利用和便于储存等优点，已应用于桁架式展开天线[7]和星际探索机器人[8]等领域。姚燕安等[9]以3RRS并联机构为本体提出一种多面体网型空间抓捕机构。刘洋等[10]利用Bricard机构的缩放和翻转特性实现对接目标的夹持和推送。但上述研究忽略了复合机构之间的运动耦合，仅对其简化模型进行了分析。

并联机构具有很强的耦合性，难以直接采用D-H等传统串联机构运动学建模方法[11]进行分析。3RRS机构一般选取末端球副中心建立动平台坐标系，利用其与定平台之间的连杆约束求解运动学。郭玉[12]和倪仕全[13]等分别应用闭环矢量法和几何法获得3RRS逆运动学的解析表达。李大海等[14]基于3个连杆约束方程采用牛顿迭代法对其正运动学求解。马春生等[15]采用代数消元法，将约束方程化简为一元高次方程进行数值求解。但是，数值法求解效果依赖于迭代初值，计算量大且不适用于奇异位形[16]。因此，通过增加传感器获取机构额外的状态信息，可适当简化并联机构正运动学求解[17]。Bricard机构利用连杆闭环方程得到输入及输出角度之间的关系[18]。马艳等[19]采用几何法得到闭环环路方程。Shang等[20]分析了三重对称Bricard机构中几何参数和关节转角之间的关系。

但是针对具有多闭环回路的3RRS-Bricard复合系统，由于3RRS、Bricard、消旋机构和卫星平台之间的运动相互耦合，难以直接采用上述方法分析其运动学。Angeles和Kecskemethy[21]提出将闭环回路“切断”转换为树型运动链，基于“切断”处运动约束求解复杂闭环链的方法，并将其推广到闭环系统多体动力学建模的应用中[22]。VREP(Virtual Robot Experimentation Platform)仿真平台[23]结合该方法，实现对并联机构建模和正、逆运动学求解，采用阻尼最小二乘法(Damped Least Squares，DLS)[24]以避免陷入局部最优解。但是该方法容易在极限位置附近产生较大误差，且不适用于计算能力受限的星载计算机。

针对上述问题，本文开展基于Bricard和3RRS机构的可折展复合捕获系统运动学研究。通过构建Bricard与3RRS间的转换关系，实现捕获系统各机构间的运动学解耦；结合空间捕获系统的构型特点，设计复合系统的运动学解析求解方法，并在仿真环境下开展针对动态捕获目标的轨迹跟随实验。

1 复合捕获系统的组成和特点

1.1 捕获系统的组成和自由度分析

基于3RRS-Bricard的复合捕获系统通过变刚度旋转关节与搭载卫星相连，其组成如图1所示。系统整体具有7个自由度，通过控制Bricard、3RRS、变刚度关节和搭载卫星间的协同运动，实现对捕获目标的夹持、消旋、位姿调整和捕获。

Bricard由6根等长连杆和6个转动副组成，且首尾连杆相连形成闭环运动链。机构整体具有1个缩放自由度，可通过变形实现针对不同形状和尺度捕获目标的夹持操作。3RRS[25]并联操作机构由3条支链组成，每条支链上依次安置了2个转动副(R副)和1个球副(S副)，其中第一个转动副为主动，另一个为从动。当Bricard运动状态确定时，3RRS机构具有3个自由度，在卫星参考坐标系下，分别是沿z方向的移动、绕x轴和y轴的转动。卫星平台保证系统x和y方向移动的机动能力。变刚度关节可在卫星坐标系下绕z轴转动，通过调整自身刚度消除捕获目标沿自身惯量主轴的旋转运动。根据捕获目标运动状态，3RRS机构协同卫星平台和变刚度关节调整系统位置和姿态，从而避免过大交互力并提高消旋效率，为成功抓捕目标提供保障。

1.2 驱动和传感器布局

根据1.1节的自由度分析，综合考虑机构折展过程中连杆运动干涉和受力情况，分别在3RRS顶部3个主动副和Bricard远离3RRS球副的3个相间转动副上安装驱动电机和角度传感器，保证缩放过程中Bricard 3个驱动关节转角相等，从而实现机构的稳定运动和精准伺服控制。并且在3RRS其余3个从动转动副上安装绝对位置编码器，以降低3RRS机构正运动学求解的复杂度。为实现柔顺的目标捕获，避免过大的交互碰撞力，在变刚度旋转关节和3RRS-Bricard复合抓捕机构中间安装有六维力矩传感器，从而实现抓捕系统基于力和力矩反馈信息的位置和姿态调节。

1.3 构型特点

Bricard从动副与3RRS支链末端球副通过共享转动轴的方式连接在一起，如图2所示。用Bricard机构充当3RRS并联机构的动平台，形成如图1所示的复合捕获系统。针对不同形状、尺度的目标，捕获系统可以通过夹持和吞噬2种方式进行捕获，如图3所示。

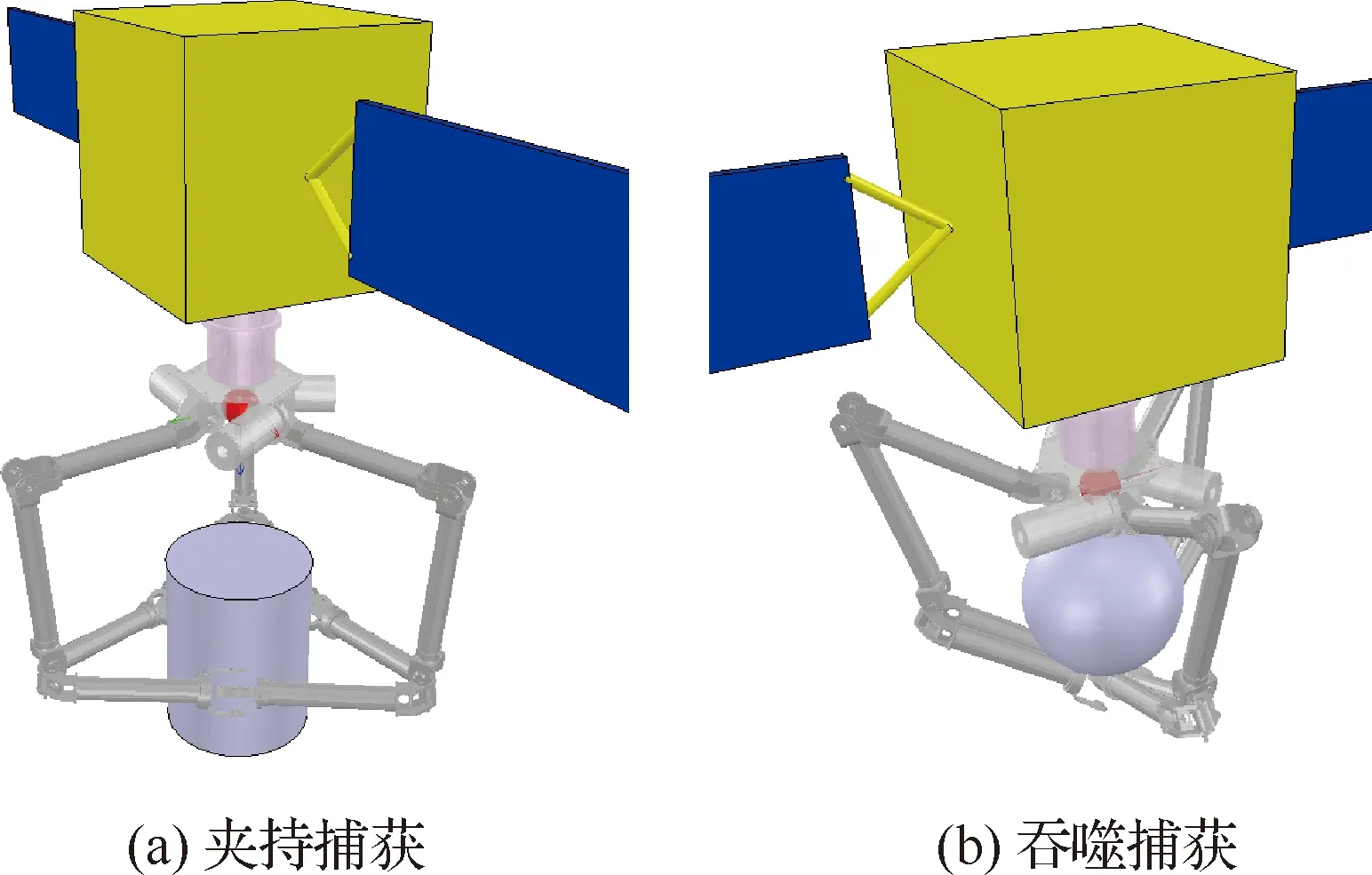
复合捕获系统同时继承了Bricard和3RRS的缩放和折展特性，但是其运动学特点与传统的3RRS和Bricard机构又有所不同。

1) 针对小尺寸目标的夹持捕获和各尺度、形状非合作目标的吞噬捕获，连杆顶点处采用弯折设计

如图2所示，弯折设计虽然可有效扩大捕获系统的适用范围，避免Bricard相邻连杆在完全收拢时产生运动干涉，但导致从动关节和主动关节的公垂线与连杆所在平面发生偏移，几何特性的变化增加了Bricard运动学求解难度。

2) 3RRS并联机构运动学求解的关键在于建立球副所在动平台与定平台之间的转换关系

球副位于Bricard从动副的转轴延长线上，转轴姿态取决于Bricard机构的缩放程度，导致3RRS并联机构和Bricard机构的运动耦合复杂化。因此，3RRS机构的运动学求解依赖于Bricard的运动状态和两者间的运动关系，不能基于关节融合[9-10]的简化模型求解复合系统运动学。

3) 以Bricard 3个驱动关节(夹持点)中心作为系统的运动学控制目标实现对捕获目标位姿的直接控制

3RRS机构、变刚度旋转关节和卫星平台的运动对Bricard目标点位姿的影响相互耦合，难以采用传统的运动学分析方法对该7自由度复合式捕获系统进行求解。

2 运动学分析

2.1 运动学解耦

基于1.3节的构型特点，首先需要构建Bricard与3RRS机构间的运动学转换关系，使Bricard、3RRS、变刚度旋转关节和卫星平台之间运动学解耦，再分别根据Bricard和3RRS的运动和几何特点进行求解。

Bricard驱动关节中心坐标系，即夹持点中心相对于卫星坐标系的位姿转换关系按照系统由上到下的顺序可写为

SatTB=SatTJJT3RRS3RRSTSSTB

(1)

式中：jTq为坐标系{q}相对于坐标系{j}的齐次转换关系；Sat、J、3RRS、S和B分别代表卫星、变刚度关节、3RRS并联机构定平台、球副中心(3RRS动平台)和Bricard驱动关节中心坐标系。因此，Bricard驱动关节i的位置SatNi可由式(2)得到：

SatNi=SatTBBNii=1,2,3

(2)

复合捕获系统中Bricard参数满足3个几何特征：① 6个连杆长度相等；② 杆1、3、5两端转动副轴向偏转α，杆2、4、6两端转动副轴向偏转2π-α；③ 相邻连杆在转动副轴线方向上的偏距为0。因此该Bricard机构具有三重对称性[26]，即各旋转副之间具有120°旋转对称的性质，相间关节角度相等。因此，Bricard中心坐标系下，其机构缩放大小Bs与3个驱动关节位置BN1、BN2和BN3的关系为

(3)

由机构的自由度分析可知，式(1)中的齐次转换矩阵可进行改写：

(4)

式中：Transl([px,py,pz])为沿x、y和z轴分别平移px、py和pz的齐次转换；Rotx(rx)为沿x轴旋转rx的齐次转换，Roty(ry)和Rotz(rz)同理。

将式(1)中，Bricard驱动关节中心相对于3RRS动平台的转换关系STB左移，可得转换关系：

Transl([px,py,0])·Rotz(rz)·

Transl([0,0,pz])·Roty(ry)·

Rotx(rx)=Transl([px,py,pz])·

Rotz(rz)·Roty(ry)·Rotx(rx)

(5)

由此可以看出，此时捕获系统中卫星平台、转动关节和3RRS动平台在运动学上相互解耦，即整个捕获系统在某一个自由度上的位置或姿态变化只与上述某一特定机构的运动状态相关。因此，可根据球副中心相对于卫星的位姿转换矩阵SatTS，直接求取卫星平台和变刚度关节的运动控制量px、py和rx，并获得3RRS动平台的目标位姿3RRSTS，进而求解其逆运动学。

2.2 Bricard与3RRS的运动学转换关系

利用正六棱柱模型可以直观表达Bricard驱动关节和3RRS球副之间的运动学几何特性[27]，如图4所示。由Bricard的三重对称性可知机构相间3点所构成的平面是相互平行的。3RRS并联机构支链末端球副分别位于Bricard 3个从动副转轴的延长线上，且到从动副轴心的距离相等，因此球副之间同样具有120°旋转对称性，即球副中心Sc、Bricard驱动关节Nc、虚拟顶点中心Mc和从动副中心Pc四点共线，且其连线垂直各中心点所在平面。

Bricard与3RRS运动学转换关系如下：

STB=Transl([0,0,h])

(6)

式中：h为Bricard驱动关节中心SNc在3RRS动平台坐标系S下沿平台法向，即z轴方向产生的偏移，其大小由Bricard缩放Bs决定。因此先对Bricard机构进行运动学求解，从而获得Bricard与3RRS机构动平台之间的转换关系。

2.2.1 Bricard运动学求解

如图4所示，通过引入Bricard从动副两侧连杆的虚拟顶点M1、M2和M3，避免连杆弯折设计对机构几何特性和运动学求解的影响。在Bricard机构N1M1N2M2N3M3中，相邻关节的公垂线位于连杆轴线上，根据闭环特性，可知各个连杆间的齐次变换矩阵依次相乘为单位矩阵[27]：

N1TM1M1TN2N2TM2M2TN3N3TM3M3TN1=I

(7)

由式(7)可得Bricard从动副转角β1和驱动关节转角β2之间的约束关系为

cos2α(cosβ1+cosβ2-cosβ1cosβ2-1)-

cosβ1-cosβ2-cosβ1cosβ2+

2cosαsinβ1sinβ2=0

(8)

式中：α为Bricard相连连杆轴向之间的偏转角度，α= 30°。

Bricard缩放大小Bs=|N1Nc|=|N2Nc|，在图5所示的三角形ΔN1M1N2中，Bs与β1之间存在几何关系：

(9)

2.2.2 Bricard到3RRS动平面距离

3RRS动平台中心Sc到Bricard驱动关节中心Nc的距离h=h1-h2+h3，h1、h2和h3分别表示Mc到Nc、Mc到Pc和Sc到Pc的距离，如图6 所示。

在三角形△N1Q1Q2中，h1=|N1Q2|，可通过式(10)进行求解：

(10)

在图6中，直线M1Mc、P1Pc和S1Sc相互平行且垂直于直线ONc,由三角形的相似性可知，h2与h1之间具有运动学关系：

(11)

式中：|NmP1|为机械设计参数，为固定值；h2与h1同向；h3垂直三角平面△M1M2M3，方向为正，可通过式(12)求解：

h3=|P1S1|cosφ

(12)

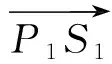
φ=arcsin(h2/|P1M1|)

(13)

由此可得Bricard夹持点中心与3RRS动平台之间的运动学转换关系STB。

2.3 3RRS运动学求解

2.3.1 3RRS正运动学求解

3RRS通过在从动副θ4、θ5和θ6安装角度传感器，实时感知运动信息避免迭代计算，从而简化机构的正运动学求解。如图7所示，点A1、A2和A3构成3RRS机构定平台平面，3点间120°旋转对称。以A1-B1-S1支链为例，在给定θ1且θ4已知的情况下，S1相对3RRS定平台的位置为

3RRSS1=3RRSTA1Rotz(θ1)·Transl([0,0,L1])·Rotz(θ4)·Transl([0,0,L2])·[0,0,0,1]T

(14)

式中：3RRSTA1是点A1相对3RRS定平台的位姿矩阵，为固定值；L1和L2分别为3RRS机构的上下连杆长度。

按式(14)可分别求取球副S1、S2和S3的位置，该三点中心为Sc，即3RRS并联机构动平台(球副中心)坐标系S的原点，姿态与Bricard夹持平面一致，z方向垂直于球副平面指向远离定平台的方向，y方向由S1和S3的中点Sm指向Sc，可通过右手定则求取x轴方向。

2.3.2 3RRS逆运动学求解

S1、S2和S3绕点Sc120°旋转对称，相对于动平台的位置为

(15)

3 仿真分析与实验验证

针对7自由度多运动副复合式捕获系统，在V-REP[23]机器人仿真环境下搭建运动学和动力学模型。

3.1 仿真环境下运动学建模

传统的串联型机器人常采用一般机器人描述格式(Unified Robot Description Format，URDF)[28]建立连杆与关节之间的树型关联，进而描述系统的运动学关系并进行求解，但是不能直接应用于具有闭链的并联系统。针对本文具有多闭环的3RRS-Bricard复合捕获系统，由于卫星平台、变刚度关节与3RRS-Bricard可折展机构间可实现运动学解耦，因此，重点研究可折展机构的运动学建模。首先，确定3RRS-Bricard复合机构中具有独立控制变量的闭环运动链。选取在固定位姿的连杆处“切断”环形运动链转换成树型父子结构，通过在“切断”处补充运动约束将闭环运动学问题转化为给定两端位姿的串联机构求解，且该串联运动链中，任意连杆的运动状态受其父节点和子节点的共同影响，具有闭环运动特性。

用XY移动平台等效卫星的平移运动，3RRS-Bricard机构中共存在3个闭环运动链，如图8所示。闭环运动链从一个固定位姿的连杆(关节1的父连杆)开始，依次通过其相连关节和连杆，直至回到起始连杆或到达另一个相对位置固定的连杆(关节2和3的子连杆)。Bricard驱动关节的中心为目标控制点，根据捕获目标的位姿确定夹持点Nc相对于卫星平台的转换矩阵SatTB。根据捕获目标的尺寸决定Bricard的缩放大小Bs，结合式(3)求取运动学模型中的目标控制点位置SatN1、SatN2和SatN3。继而求得Bricard驱动关节中心Nc到3RRS动平台球副中心Sc的距离h，获得球副中心相对于卫星平台的转换关系SatTS，从而实现卫星平台、变刚度关节和3RRS-Bricard复合机构间的解耦：

(16)

根据目标点的位置在仿真环境下利用阻尼最小二乘法求解3RRS-Bricard机构的运动学，从而实现系统的协同控制。

3.2 比对实验

针对运动状态实时变化的捕获目标，分别采用提出的先解耦再基于各机构几何特征的分析方法与集成在V-REP仿真环境中基于闭环约束的阻尼最小二乘法对捕获系统的运动学进行求解，并将求解结果发送给动力学模型驱使其运动。通过比对动力学模型跟随目标轨迹的运动精度验证算法的有效性和先进性。系统动力学模型的主要参数如表1所示，卫星XY移动平台、变刚度关节、3RRS上臂杆和Bricard驱动关节的驱动力大小分别为1 000、115、79、33 N·m。

在动力学模型中，从动副关节的驱动力设为0，跟随驱动关节运动。仿真环境重力方向的加速度为0，模拟太空零重力环境。给定的目标轨迹位于沿z轴距离卫星平台1.38 m的圆弧平面上，且该圆弧绕过圆心的x和y轴依次旋转5°和10°。轨迹上点坐标系的z轴垂直平面远离卫星平台，y轴指向圆心，每个点依次绕x和y轴转动5°和20°。

表1 系统动力学模型的主要参数Table 1 Main parameters of system dynamic model

图9为捕获系统基于几何特征求解运动学的方法实现目标轨迹跟随的协同运动过程。其中，紫色球是跟随轨迹目标点，红色球由上至下分别代表卫星平台、3RRS定平台和Bricard夹持点中心坐标系。

由图9所示，在轨迹跟随实验中Bricard夹持点位姿几乎与目标点完全重合，可直观判断该运动学求解算法的有效性，验证了捕获系统具有各个机构间平稳协同运动的能力。基于不同运动学分析方法求解捕获系统运动学的轨迹跟随实验效果和精度对比分别如图10和图11所示。

图10中，红、绿、蓝射线分别代表目标姿态的x、y和z轴线方向。通过比对图10(a)和图10(b)可以看出，基于几何特征的求解结果明显优于阻尼最小二乘法。动力学系统受驱动力限制，具有微小的延迟性，基于几何特征的求解结果在运动过程中三轴最大位置误差小于4 mm，平均运动精度为1.867 mm，最大姿态误差小于0.035 rad，平均运动精度为0.021 rad；然而由于部分轨迹点靠近其极限位姿，基于阻尼最小二乘法的求解结果在运动过程中三轴最大位置误差为34.636 mm，平均运动精度为24.986 mm，最大姿态误差为0.043 rad，平均运动精度为0.032 rad，如图11所示。

4 结 论

1) 捕获系统同时继承了Bricard和3RRS机构的缩放和折展特性，结合复合机构的连接特点，通过建立Bricard与3RRS的运动学转换关系实现多机构间的运动学解耦，为该类多从动副7自由度复合并联系统的运动学建模和协同控制提供有效准确的解决方案。

2) 通过引入Bricard从动副两侧连杆的虚拟顶点，避免连杆弯折设计对运动学特性的影响。基于六棱柱模型并利用Bricard机构三重对称的几何特性，通过在3RRS机构从动副上安装角度传感器得到3RRS-Bricard复合机构正、逆运动学求解的解析表达。

3) 在机器人仿真环境下搭建了捕获系统的运动学和动力学模型，通过与基于闭环约束的阻尼最小二乘法进行运动学求解的实验对比，验证了所提基于几何特性的运动学求解算法在动态轨迹跟随上具有明显的精度优势。

4) 在今后的研究中，应综合考虑捕获目标尺度和形状的变化范围，根据应用场景适当简化和优化系统构型，推广其工程应用。