基于旋转式IMU地下管线轨迹探测系统*

张新宇, 陈 强, 杨文龙, 徐甲栋, 陈孟儒, 李 睿

(上海工程技术大学 电子电气学院,上海 201620)

0 引 言

目前随着城市建设的迅速发展,城市地下管线铺设越来越错综复杂,很多老旧地下管线数据丢失,这些问题会对城市地下管线的规划管理、建设施工以及地下空间的合理利用产生重大影响[1],如天然气爆炸、水管断裂、排污管道断裂等。为了保证项目施工可以安全进行,在施工前首先获取施工区域地下管线分布与位置情况是必然的需求[2]。由于地下管线轨迹的测量过程复杂并且精度受诸多因素影响,所以出现了很多种测量技术与方法。例如:文献[3]中研究的一种以高精度的电子罗盘为核心元件的非开挖地下管线轨迹探测装置,但该装置易受地磁影响,并且操作复杂；英国雷迪公司的RD系列管线轨迹探测仪,主要基于电磁感应的工作原理,导致仪器在遇到诸如水分较大、电阻率不平衡等土壤地质环境中工作时的误差极大,城市空间中的强电磁信号也会对其产生干扰[3]。所以，研究一种高效、低成本,精度达到要求的管线轨迹测量系统在工程上是一种必然选择。

本文研究的基于旋转式IMU地下管线轨迹探测系统,选用单轴光纤陀螺仪、加速度计、霍尔传感器多传感器融合。采用欧拉角旋转矩阵原理,设计算法与数学平台。该系统有着施工周期短、环境影响小、综合成本低等独特优势。整个测量系统,其主要构成有负责追踪姿态角变化及距离信息的以传感器为核心的硬件部分和负责数据解算并绘制三维轨迹图的软件部分。

1 系统总体方案设计

1.1 硬件平台设计

系统的硬件结构组成部分有前后拉环、滚轮计程装置、三爪行进轮、电路仓、操作台、电池仓。仪器内部传感器的设计如图1所示,其中单轴光纤陀螺仪加入文献[4]中提出的自重装置,以防止仪器在测量过程中翻滚时造成的误差,两个加速度计传感器的敏感轴均与坐标轴平行。

图1 传感器设计

利用仪器测量管线轨迹数据时,采用多传感器融合[5]法测量出实时的姿态角[6]与行进距离变化数据,将测到的数据利用芯片STM32F103RCT6存储到Flash芯片W25Q64中,等待PC机通过串口对数据读取、保存并解算。

1.2 软件平台设计

1.2.1 软件环境

本文研究的系统考虑到后期需要对大量的数据进行解算,为了能够更快速地处理数据以及对PC硬件要求限制等因素,在Windows10系统下采用Visual studio 2017平台利用C语言编写程序进行数据解算,C语言不仅运行速度快,而且可移植性强。利用Python对地下管线轨迹进行三维画图。

1.2.2 软件功能模块设计

软件功能模块主要分为四个部分：读取数据并保存；数据预处理；数据解算；绘制三维轨迹图。软件设计流程如图2所示。

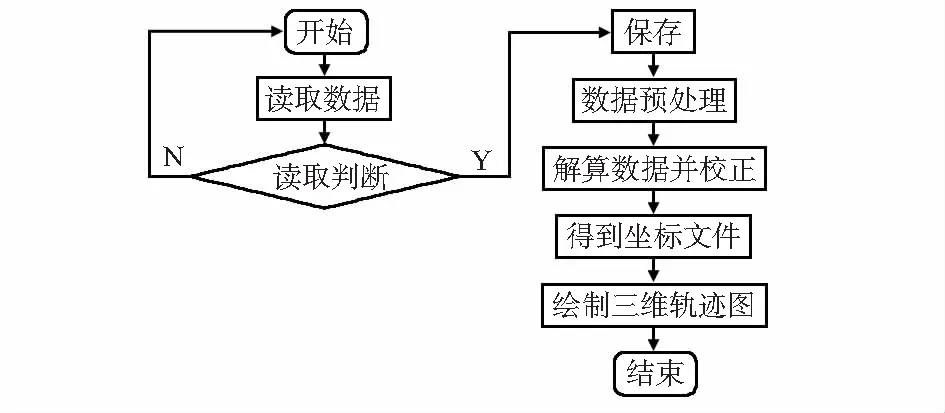
图2 软件设计流程

2 坐标解算与轨迹求取

2.1 确定坐标系

解算时，首先确定两个坐标系,一个为大地坐标系O-XYZ,另一个为载体坐标系O-xyz,载体坐标系与探测仪固联,随着仪器的运动而转动,大地坐标系保持不动,在坐标系中规定仪器行进的方向为X轴(大地坐标系的东方向)[7],并且以右手定则规定旋转正反方向,如图3所示。

图3 大地坐标系与载体坐标系

2.2 线速度解算原理

当滚轮计程装置中的霍尔传感器与磁钢之间相对位置变化时,霍尔传感器感受到的磁感应强度也随之变化,从而导致传感器的输出电压改变[8],滚轮内嵌的磁钢每次经过霍尔传感器时会输出一个低脉冲。当滚轮转动一周时,在滚轮没有打滑的理想情况下,刚好会记录到6个低脉冲,滚轮直径d经过测量大约为0.074 m,由此可计算出滚轮上两个磁铁之间对应滚轮的圆弧距离L(m)。仪器采集数据的频率为每秒钟记录100组数据,所以记录每组数据的时间t大约为0.01 s。在解算的过程中,首先会读取每一组数据的霍尔值,当霍尔输出值有两次变化时,记录中间霍尔输出值没有变化的组数Ni,用于计算每次霍尔有变化时经过的时间,此时进行一次数据的解算(等距采样解算)。这样就可以计算出X轴方向的线速度Vi(m/s)以及加速度ai(m/s2)。等距采样下的瞬时线速度与加速度计算过程如下

(1)

(2)

2.3 姿态角解算原理

姿态角由单轴光纤陀螺仪、加速度计测量所得。本文研究的系统中规定围绕坐标系X轴,Y轴,Z轴旋转的分别为翻滚角φ,俯仰角θ,方向角ψ。

翻滚角φ和俯仰角θ的解算以重力加速度矢量b=[0,0,-gn]T为参考量[9],当加速度计的敏感轴与矢量B的方向处于非垂直的状态时会产生gn(取9.8/s2)的分量,此时就可以通过gn的分量与矢量b计算出翻滚角φ和俯仰角θ。规定旋转顺序为依次围绕Z轴,Y轴,X轴旋转,解算过程如下：

围绕X轴,Y轴,Z轴的欧拉角旋转矩阵分别为

坐标轴上gn的分量分别记为ax(m/s2),ay(m/s2),az(m/s2),与参考失量b的关系为

(3)

解算出的翻滚角φ和俯仰角θ分别为

(4)

式中ax,ay均为通过加速度计测量出的电压值根据产品手册给出的其比例因子计算所得。但是由于探测仪在管道中测量时无法达到理想的匀速状态,所以仪器自身在向前运动的时候也会产生一定的加速度叠加在ax上,所以在求解每一采样点θ时需要在式(4)中的ax减去式(2)计算出的ai。

方向角ψ解算同理,此时只能测出仪器围绕Z旋转后的角速度,所以可以通过旋转矩阵逆变换求得仪器旋转前Z轴方向的角速度[10],因为仪器在真实测量过程中无法保证匀速运动,所以在X轴与Y轴上也存在着角速度变化从而影响Z轴的角速度变化。经过矫正后的计算公式如下

Wz=-sinθωx+cosθsinφωy+cosθcosφωz

(5)

ψ=Wz×Ti

(6)

式中ωx,ωy,ωz为变换后各轴上的角速度,单位为(°)/s。

2.4 坐标与轨迹求取

将解算出的姿态角代入旋转矩阵,根据式(1)计算的线速度记为vxi经过旋转逆变换得到仪器在旋转前X，Y，Z三轴方向上的速度分量,分别记为Vxi，Vyi，Vzi,单位为m/s,再将每一方向上的速度分量乘以两采样点之间的时间间隔Ti得到两个采样点之间的距离矢量,对每次解算出的距离矢量进行逐点累加得到每个采样点的相对坐标,记为[DxiDyiDzi]T,由于本文研究的系统是在相对坐标系下完成的,所以起点坐标设为(0,0,0),坐标求取公式如下

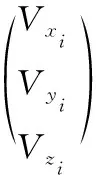
(7)

最后将三维点坐标相连得到最终所需要的地下管线三维轨迹。

3 系统实现与数据分析

为了验证本文研究的系统可行性,在室外搭建了一根长约6 m的PVC模拟管线进行模拟实验。通过实地测量,利用设计的上位机在相对坐标系下对数据解算,并绘制出的模拟管线三维轨迹。如图4所示。该系统解算出的坐标数据为相对坐标系下的坐标,在实际工程测量中,可以利用RTK载波相位差分技术测量出管道入口大地坐标与高程,在此基础上,加上测量出的相对坐标即可得到可在工程上应用的大地坐标。

图4 模拟管线与三维轨迹

将三维轨迹图平面展开分别投影在X-Y,X-Z,Y-Z平面如图5所示。

图5 二维模拟管线轨迹

在轨迹探测仪实验前将管线轨迹做了一些标定点的实际测量,用卷尺测量的管线X轴方向实际长为6.05 m,Y轴向左倾斜为0.26 m,Z轴向上为0.29 m。然后使用地下管线轨迹探测仪经过反复大量实验测试,测得数据经过上位机解算,其中3组数据如表1所示。

经过分析得到的轨迹坐标数据比较稳定,X轴方向测量长在5.42～5.47 m之间,Y轴方向测量向左0.32～0.37 m之间,Z轴方向向上在0.26～0.31 m之间。其中,X轴距离和实际测量差距大的原因是：轨迹探测仪在管道内占据一定长度的距离,使得偏差较大,除去轨迹探测仪所占的0.52 m后,X轴误差在可接受范围内。Y轴,Z轴也均在工程可接受范围内。经过分析总结,误差主要分为三点：机械误差、传感器误差和算法误差。

表1 三组部分数据

4 结束语

本文研究设计的地下管线轨迹探测系统基于惯性导航测量原理,采用捷联/平台混合架构设计,多传感器融合方式,依据欧拉角旋转矩阵原理设计算法与数学平台。具有不容易受外界环境影响、操作简单、探测连续性强的优势。通过C语言编写程序对数据解算,Python语言对坐标绘制三维管线轨迹图,能够较精确得到完整地下管线轨迹。该系统可以很好地在竣工管线轨迹测量中应用,并为地下管线轨迹测量技术提供了有力保证。