机载传感器的抗定位缩比试验方法*

曾小东

(中国电子科技集团公司第十研究所，四川 成都 610036)

0 引 言

测向交叉定位系统是一种广泛应用的无源定位体制，利用多个观测站估计来波信号的到达方向(direction of arrival,DOA)对目标进行定位，具有作用距离远，隐蔽性高等优点[1～3]。为了评估载机在实际工作中对抗测向交叉定位系统的效果，需要开展空中试飞试验。然而，受试验场地、科研经费等条件限制，载机在对抗测向交叉定位系统时，定位精度往往不能在真实场景中直接考核，需要事先开展大量的缩比试验。

缩比试验在雷达散射截面积、声隐身、红外探测距离等测试方面已有大量研究。文献[4]和文献[5]研究了雷达散射截面积的测量和缩比试验方法。文献[6]采用缩比模型开展了预警机雷达天线辐射特性的测试。文献[7]基于缩比模型完成了红外搜索跟踪系统探测距离的测试。文献[8]通过缩比模型试验分析了多孔吸声材料的实际吸声效果。文献[9]建立了海面电磁缩比测量的替代模型并进行了数值仿真验证。

本文充分借鉴国内外学者在缩比试验方法上的基本思路，开创性地将缩比方法应用到载机对抗测向交叉定位系统的定位精度评估。从几何相似性和DOA测量相似性两个方面对真实场景和缩比场景进行了比较分析，为评估载机在对抗测向交叉定位系统时的定位精度提供了一种可行的验证方式。

1 测向交叉定位原理与定位精度

1.1 测向交叉定位原理

双站测向交叉定位原理如图1所示，图中观测站1(x1,y1,z1)和观测站2(x2,y2,z2)，分别对目标(x,y,z)进行测向以确定目标的位置。观测站1对目标的测量角度集为(φ1,η1)，观测站2对目标的测量角度集为(φ2,η2)[10～12]。

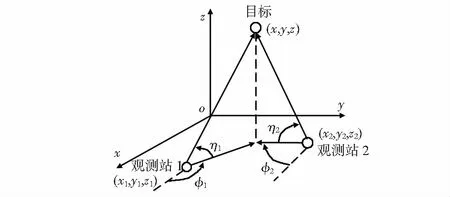
图1 测向交叉定位原理

1)目标观测方程

方位角φi和俯仰角ηi，分别为第i个观测站对目标方位角和俯仰角的观测值，i=1,2，则双站测向交叉定位的观测方程为

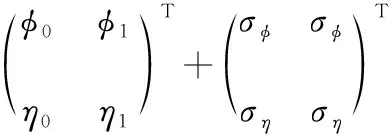
(1)

其中

(2)

式中σφ和ση为测角误差标准差σφ=ση=σθ,l=(x,y,z)为目标位置，li=(xi,yi,zi)为观测站位置。

2)导航观测方程

考虑导航误差对目标位置估计的影响，建立观测站的导航观测方程，即

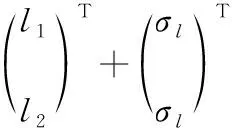
(3)

式中σl为导航误差标准差。

1.2 定位精度的克拉美罗下界

目标位置l无偏估计的克拉美罗下界(Cramer-Rao lower bound,CRLB)矩阵Rl[13]为

Rl=(A-UD-1V)-1

(4)

相应地，定位精度为

(5)

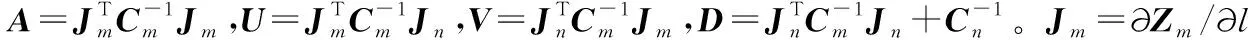
(6)

式中θ为来波方向,f为来波频率,d为阵元间距,σφ为相位差测量误差。

2 缩比模型几何场景与定位精度

2.1 缩比试验场景

双站测向交叉定位缩比模型的几何场景如图2所示，图中观测站1(x′1,y′1,z′1)和观测站2(x′2,y′2,z′2)，分别对目标(x′,y′,z′)进行测向以确定目标的位置。观测站1对目标的测量角度集为(φ′1,η′1)，观测站2对目标的测量角度集为(φ′2,η′2)。

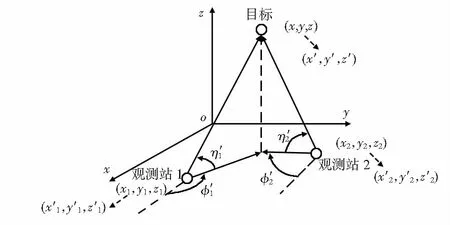
图2 缩比试验场景

2.2 缩比试验定位精度的克拉美罗下界

J′m=Jm/α

(7)

J′n=Jn/α

(8)

同时，缩比模型下，导航误差标准差σ′l=σl保持不变，故C′n=Cn。

缩比模型下，阵元间距d′=d，来波方向θ′=θ保持不变，但相位差测量误差σφ与诸多因素相关[14]，可以用测量误差因子β进行量化，σ′φ=βσφ。在缩比试验时，维持缩比前后的信号参数不变，即来波频率f′=f，由式(6)的表达式，得出σ′θ=βσθ，则C′m=β2Cm。

由缩比前后的雅可比矩阵和协方差矩阵可推导出

(9)

(10)

(11)

(12)

最终

R′l=(A′-U′D′-1V′)-1

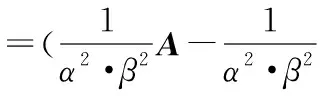
(13)

(14)

由式(7)和式(8)的推导可以看出，在缩比模型的几何场景下，目标位置和观测站位置的缩比，会影响雅可比矩阵Jm和Jn，影响的因子为1/α，同时也会影响协方差矩阵Cm，影响的因子为β2。但需要注意的是，在缩比试验时，需要维持缩比前后信号的来波方向θ′=θ,来波频率f′=f不变，同时也对观测站的测角精度性能提出了更高的要求，相比于真实场景，相位差测量误差的测量性能需要提高β倍。当然也可以改变思路，在观测站测量性能无法提高的情况下，可以将来波频率增大β倍，理论上可以取得两种情况下定位精度的CRLB不变的效果。

3 仿真分析

在试验场景中，目标机的位置为(200/175/150/100,0,8)km，观测站长机的位置为(0,20,8)km，观测站僚机的位置为(0,-20,8)km。试验的测角误差标准差为1°，导航误差标准差为50 m。几何缩比因子α范围取0.1～1，步进为0.001。测量误差因子β范围取0.1～1，步进为0.001。

当几何缩比因子α取0.1，测量误差因子β取0.5时，缩比试验的结果见表1所示。目标机的初始距离为200,175,150,100 km。

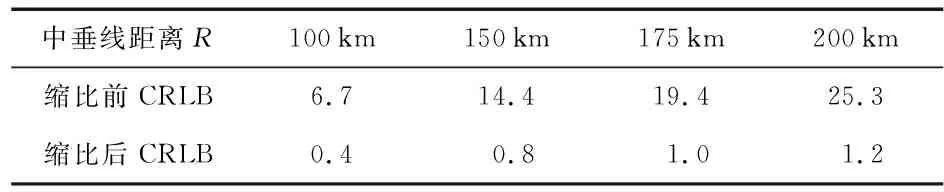
表1 缩比试验的结果

由表1可以看出，在试验场景中，缩比后的CRLB较缩比前的CRLB呈非线性的比例减小，并且由于真实场景的CRLB随距离的增加，其恶化速度大于缩比场景的CRLB，缩比前后CRLB的比值随着距离的增大而增大。因此，在缩比试验场景中，可以选取近距离的缩比试验即可。

试验场景下，测向交叉定位的缩比定位精度随几何缩比因子α和测量误差因子β的变化如图3所示，目标机的初始距离为200,175,150,100 km。

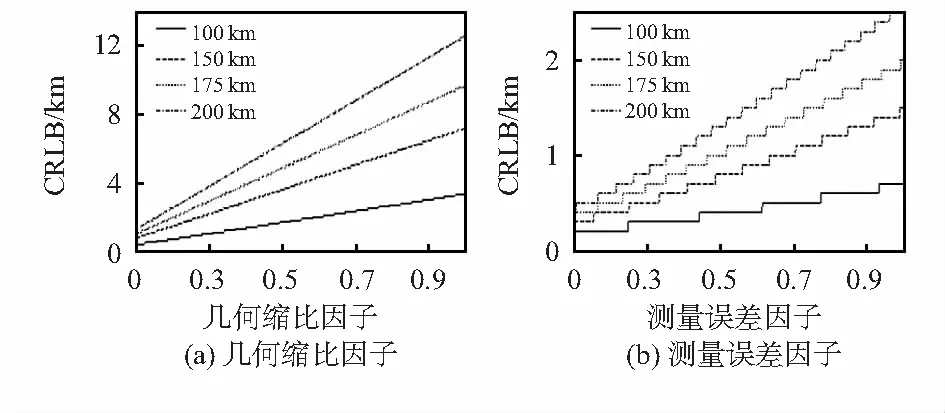
图3 缩比定位精度变化

在测量误差因子β一定的前提下，由图3(a)可以看出，在同一距离下，缩比场景的CRLB随着几何缩比因子α的增加而增加；在同一几何缩比因子α中，缩比场景的CRLB又随着距离的减小而减小。在几何缩比因子α一定的前提下，由图3(b)同样可以看出，在同一距离下，缩比场景的CRLB随着测量误差因子β的增加而增加；在同一测量误差因子β中，缩比场景的CRLB又随着距离的减小而减小。几何缩比因子α的影响程度高于测量误差因子β。

4 结 论

本文的研究利用测向交叉定位系统真实场景与缩比场景的相似性，通过对缩比前后定位精度的定量分析，得出了缩比场景下定位精度的变化规律并通过仿真实验结果证明了采取缩比试验方案的可行性，可为开展载机对抗测向交叉定位系统的定位精度评估的飞行验证提供参考依据。