基于正交实验的机器人砂带磨削工艺分析及优化*
刘建春,陈博伦,林晓辉,邹朝圣
(1.厦门理工学院机械与汽车工程学院,福建 厦门 361024;2.厦门万久科技股份有限公司,福建 厦门 361024)
0 引言
机器人砂带磨削在现代制造领域占据着非常重要的地位,尤其是在某些关键零部件的生产制造中发挥着巨大优势。工件表面材料会在砂带磨粒滑擦、耕犁和切削的作用下被去除,这三个过程都发生在磨粒与工件表面产生不同程度的挤压情况下[1-2],这就意味着磨粒和工件表面的挤压可能会导致加工表面发生塑性变形、去除过多、去除过少或裂纹等对表面质量产生负面影响的现象。而磨粒与工件表面的挤压作用又与磨削参数有着密不可分的关系[3],所以对砂带磨削工艺的研究引起了不少国内外学者和研究人员的重视。
Huang Zhi等[4]通过试验得出砂带线速度、砂带粒度、工件进给速度三个磨削工艺参数对材料表面质量影响较大的结果。符志华等[5]探究了砂带磨粒的类型、砂带线速度、工件速度等因素对材料去除效果的影响。刘月明等[6]针对复杂曲面研究了砂带线速度、砂带目数对材料去除率、表面硬度及粗糙度的影响。
上述研究主要针对单个磨削工艺参数对工件表面质量影响,对于多个因素对工件表面质量共同作用的效果没有进行进一步的研究。
Xiao Guijian等[7]采用正交试验的方法进行砂带磨削试验。通过对加工结果的分析分别得到了材料去除率、砂带磨损率及磨削比最佳的试验参数。但并没有综合考虑试验指标得出最优工艺参数组合。WU Xiaojun等[8]对磨抛材料进行单因素和正交试验,最终得到当砂带目数320 #,磨削速度4500 r/min,进给深度0.4 mm,进给速度80 mm/s时,磨削效果最好。段练等[9]基于正交试验结果和多元线性回归分析,建立了以砂带磨削深度、表面粗糙度、表面硬度为因变量,砂带线速度、磨削压力、进给速度、砂带目数为自变量的一阶回归方程,得到了具有一定可靠性的预测模型。Qi Junde等[10]基于反向传播神经网络,建立了输入为最大切削深度、砂带线速度、工件进给速度,输出为工件表面粗糙度的预测模型。
本文以铜合金异构件水龙头为例,通过机器人夹持工件的磨削方式,采用正交实验和极差、方差分析方法,分析砂带线速度、工件进给量、横向进给速度、砂带粒度对表面粗糙度及材料去除深度(MRD)的影响规律,综合考虑表面粗糙度和MRD,探究其最优的工艺参数组合。并通过正交实验数据建立4个实验变量与实验结果的线性回归预测模型。
1 机器人砂带磨削方法
为实现铜合金异构件砂带磨削,设计了如图1所示的机器人砂带磨削系统。工业机器人通过弹簧夹具夹持异构件,利用机器人线性移动使异构件与接触轮产生径向进给量d,同时砂带以线速度v运转,在两个因素共同作用下实现砂带磨削的材料去除。
实验为了研究不同目数砂带磨削效果,砂带机可更换不同目数w的砂带。为了使磨削表面产生网状纹路得到更好的表面质量[11],加入使异构件沿着接触轮轴向方向的往复运动,往复运动时设置的机器人沿着接触轮轴向方向运动的线速度为横向进给速度vr。
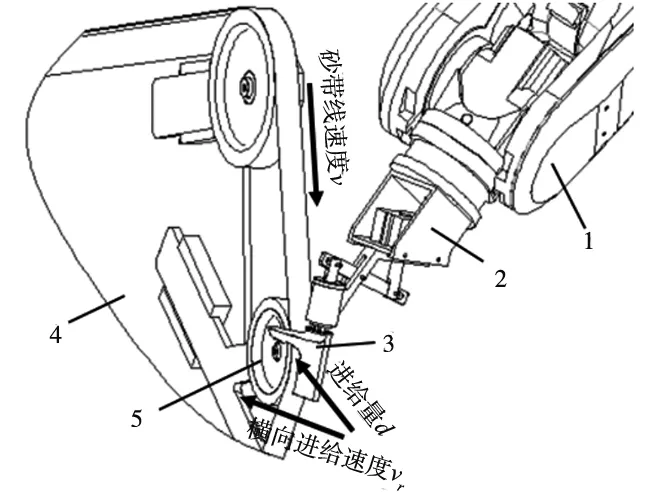
1.机器人 2.弹簧夹具 3.异构件 4.砂带机 5.接触轮
2 实验过程
(1) 实验条件
实验磨抛系统主要由工业机器人、异构件弹簧夹具、砂带机组成。其中砂带机主要由砂带、驱动轮、张紧轮、接触轮、伺服调偏装置及砂带机控制柜组成。
(2) 测试方式
实验检测设备有粗糙度检测仪和线激光检测仪,线激光检测仪通过检测磨削前后工件表面点云数据差值得到MRD。为了减小在测量过程中的误差,表面粗糙度Ra和MRD的结果均采用三次测量取平均值的方式获得。
(3) 实验方案
为减少实验次数并得到各因素对实验指标的影响,采用正交实验方法,选取L16正交阵列(四因素四水平)模型。通过企业调研结合工程经验选取磨削参数及水平见表1,正交实验方案设计见表2。
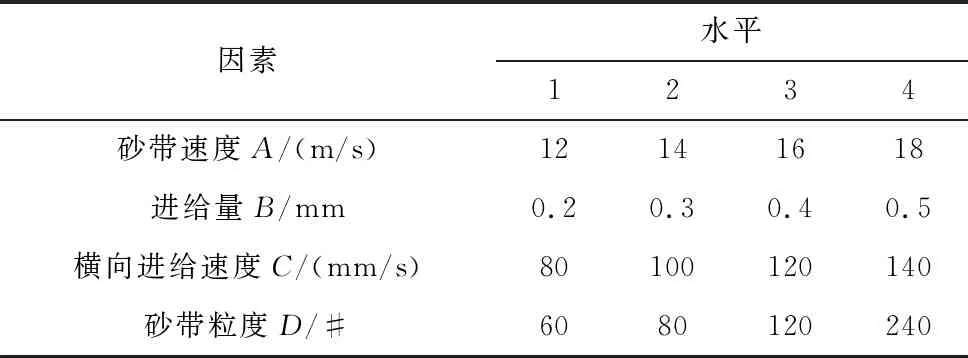
表1 正交实验因素水平
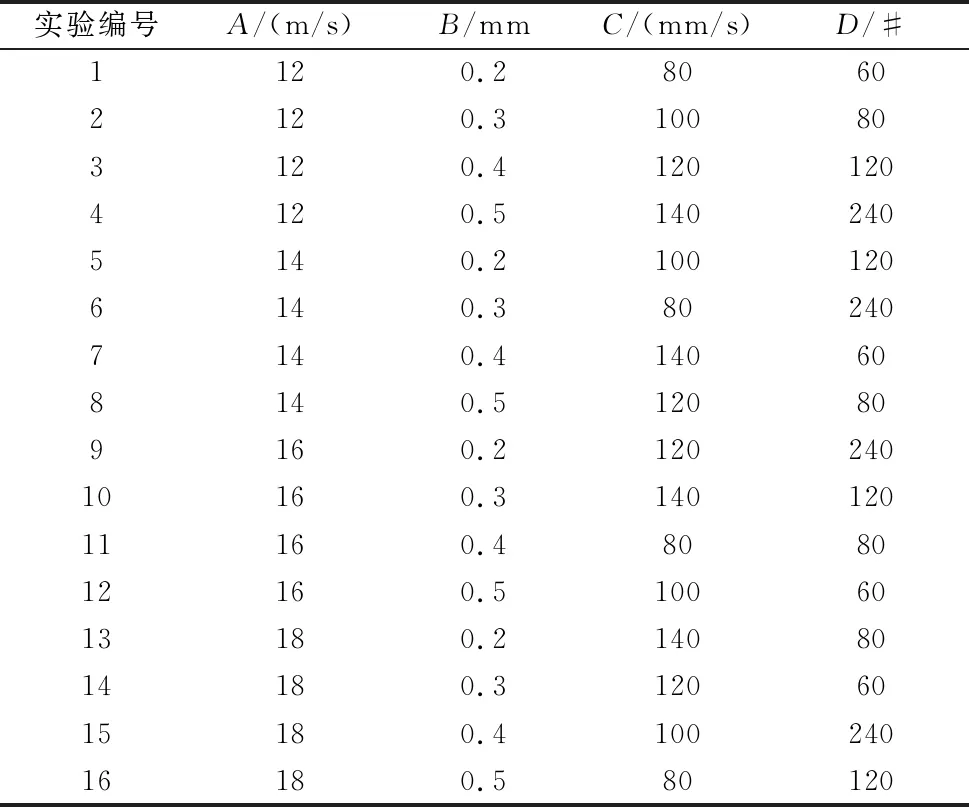
表2 正交实验方案
3 实验结果分析与讨论
为了深入分析正交实验结果,得到各个变量对工件表面粗糙度Ra及MRD的影响,通过极差和方差分析对实验结果进行数据分析。
3.1 极差分析
极差分析属于正交试验数据分析中的直观分析。通过对极差数值的分析,得到变量对工件表面质量的影响程度,根据其影响程度选取较优水平实验组合。
一般的,用Xij(i=A、B、C…,j=1、2、3…)表示因素i第j水平的变量值,Yij表示在不同变量Xij下得到的实验结果指标,则:
(1)
其中,Kij表示因素i在第j水平结果的统计参数,Yijc(c=1、2、3…d)表示在第c组实验中得到的实验结果。
一个因子的极差表示该因子各水平均值的最大值与最小值的差,即:
(2)

极差分析能够直观判断出各个因素对实验结果的影响程度并判断各指标的较优水平组合。为了深入分析正交实验数据,排除实验误差对实验结果的影响,研究各个变量对实验指标影响的显著性水平,将进行方差分析。
3.2 方差分析
方差分析可以从变量因素和实验误差两个方面解释对实验指标的影响。S总为总的实验数据变动平方和,其可分为变量因素变动平方和Sj和误差变动平方和Se,即:

(3)
(4)
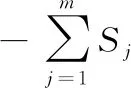
(5)
为消除变动平方和中自由度的影响,将Sj、Se分别除以对应自由度,得到均方和,最终得到F值。
(6)
其中,n为正交实验因素水平数,m为实验因素个数,d0为总的实验次数,T为所有实验指标的总和,fj为因素自由度,fe为误差自由度。F值反应各因素是否对实验结果产生显著影响。
3.3 实验结论
实验磨抛系统如图2所示,根据正交实验安排,对最终的实验结果进行测量,得到实验结果如图3所示。

1.PU轮 2.上接触轮 3.SiC砂带 4.下接触轮 5.砂带机控制柜 6.张紧气缸 7.调偏伺服电机 8.张紧轮
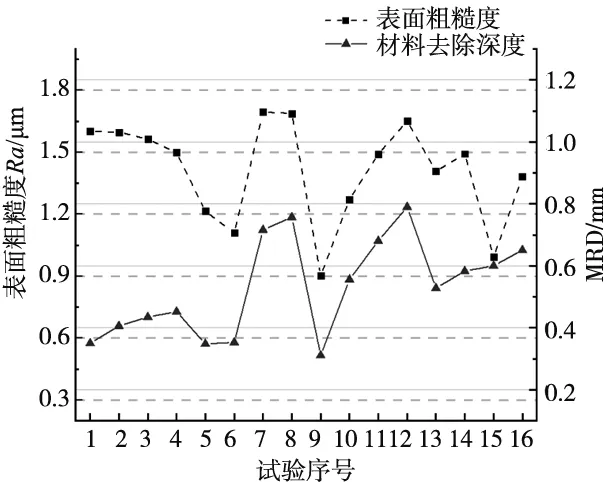
图3 正交实验结果
3.3.1 极差结果
用上述极差分析法,对本实验中的各项参数进行极差分析,其结果见表3。

表3 正交实验极差分析结果
通过对实验结果的极差分析可以得到,4个实验变量对表面粗糙度相对影响程度为:kD(0.484)>kB(0.274)>kA(0.246)>kC(0.104),即砂带目数对表面粗糙度的影响最大,横向进给速度对表面粗糙度的影响最小。同理可得实验参数对MRD的相对影响程度,即进给量对MRD影响最大,横向进给速度对其影响最小。
极差分析中各个均值大小只反映单因子四个水平上的差异,所以可通过极差分析中的综合比较得到加工参数的较优水平组合。
该病为一种排除性诊断。首先应排除各种原因所致的创伤、冻伤,这些均可导致局部瘀斑;其它的缺血性疾病也应当排除,如动脉栓塞导致的缺血、静脉血流出受损以及其它高凝状态所致的栓塞。华法林相关的紫趾综合征通常在华法林使用3~8周后发生,但开始治疗后的8h内就可能导致微循环栓塞[3];也有相关报道称,紫趾综合征在使用华法林1~10天后发生,在随后的2周进一步发展[2]。
以粗糙度作为评价标准时,根据极差分析表可得,砂带速度选择第四水平(18 m/s)时,粗糙度(Ra=1.319 μm)在四个水平中最低;进给量选择第一水平(0.2 mm)时,粗糙度(Ra=1.281 μm)最低;横向进给速度选择第二水平(100 mm/s)时,粗糙度(Ra=1.364 μm)最低;砂带目数选择第四水平(240 #)时,粗糙度(Ra=1.126 μm)最低。因此A4B1C2D4为粗糙度加工参数中的较优水平组合。同理,以MRD为优化对象时A4B4C4D1为较优水平组合。
3.3.2 方差结果
通过将实验参数代入式(3)~式(6),得到方差结果,见表4、表5。

表4 粗糙度方差分析结果
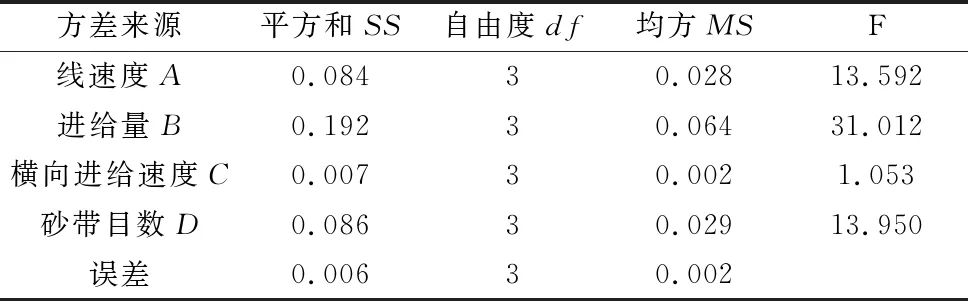
表5 MRD方差分析结果
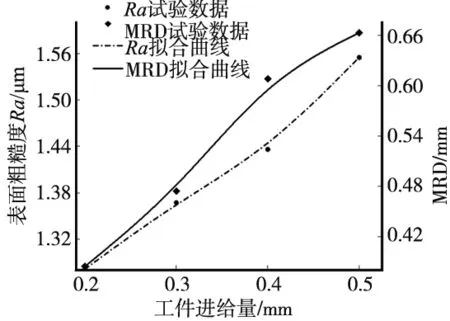
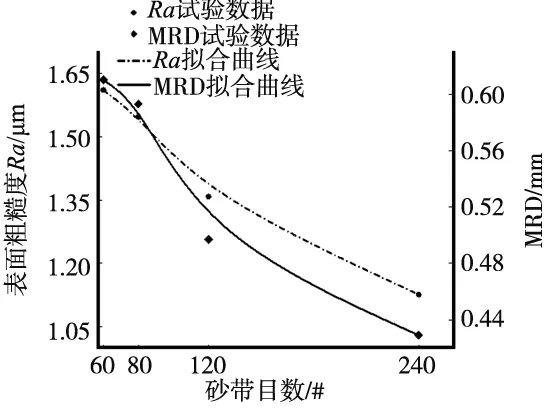
选取显著性水平α为0.1和0.01,查阅F分布表可得F0.9(3,3)=5.39,F0.99(3,3)=29.46,当F>F0.99(3,3)时称该因素对实验指标影响高度显著,当F0.9(3,3) 结合方差分析表4、表5,砂带目数D对工件表面粗糙度Ra的影响高度显著;砂带线速度A和进给量B对工件表面粗糙度Ra的影响显著;横向进给速度C对工件表面粗糙度Ra无显著影响。进给量B对MRD的影响高度显著;砂带线速度A和砂带目数D对MRD的影响显著;横向进给速度C对MRD无显著影响。 根据显著性分析可知,横向进给速度对表面粗糙度Ra和MRD都没有显著影响,所以在选择参数时可根据实际情况选择[12],这里选择使工件表面粗糙度最低的C2(100 mm/s)作为最终实验加工参数。 为更加直观研究显著影响因素和高度显著影响因素对工件表面粗糙度及MRD的影响,结合极差分析中得到的均值数据,采用B-样条曲线进行拟合,得到各因素对两个实验指标的影响趋势图,如图4~图6所示。 图4 砂带线速度对实验指标的影响趋势 图5 工件进给量对实验指标的影响趋势 图6 砂带目数对实验指标的影响趋势 图4表示砂带线速度对表面粗糙度和MRD的影响趋势,由图可知工件表面粗糙度随着砂带线速度的增大而降低。曲线斜率的绝对值不断减小,说明砂带线速度对表面粗糙度的影响程度逐渐降低。MRD随着砂带线速度增大而增大,影响程度逐渐减小;图5表示进给量对表面粗糙度和MRD的影响趋势,随着进给量的增加,工件表面粗糙度和MRD都随之增加,但对表面粗糙度的影响程度有增大的趋势,对MRD的影响程度有减弱的趋势;图6表示砂带目数对表面粗糙度和MRD的影响趋势,随着砂带目数的增大工件表面粗糙度和MRD都会随之降低,影响程度都有减弱的趋势。 通过极差分析得到,以工件表面粗糙度Ra为优化对象时,优选加工参数组合为A4B1C2D4,以MRD为优化对象时,优选加工参数组合为A4B4C4D1。在实际生产加工中,要同时保证工件表面粗糙度Ra和MRD处在较好的水平。这里引入砂带加工参数优水平评价指数[13]: 式中,zi表示极差分析中第i个工件表面粗糙度的均值,hi表示极差分析中第i个工件MRD的均值。Wi越大表示加工效果越好。各因素优水平评价指数如图7所示。 图7 实验因素优水平评价指数 根据图7可得,WA4>WA3>WA2>WA1,所以A4(18 m/s)为砂带线速度的最优加工参数。同理可得,B4(0.5 mm),D2(80 #)为最优加工参数。综上所述,实验的最优加工参数组合为A4B4C2D2。 多元线性回归是用于寻求变量与自变量之间关系的一种实验设计方法。其回归模型为: y=α0+α1x1+α2x2……αn-1xn-1+αnxn+ε (7) 即:Y=Xα+ε (8) 利用正交实验数据,通过Matlab数学分析软件建立砂带线速度v、工件进给量d、横向进给速度vr、砂带目数w与表面粗糙度Ra及MRD的回归预测模型。最终回归方程如下: Ra=1.912-0.042v+0.888d+0.001vr-0.003w MRD=-0.198+0.029v+0.968d+0.001vr-0.001w 通过拟合优度、校正测定系数和显著性检验(F检验)作为回归方程的分析结果,即: (9) (10) (11) 其中,n为样本总量,k为自变量个数,SSR为回归平方和,SSE为剩余平方和,SST为SSR与SSE之和。最终结果如表6所示。 表6 线性回归分析结果 通过正交实验得到砂带线速度、工件进给量、横向进给速度、砂带目数对工件表面粗糙度及MRD的影响,其对表面粗糙度Ra的影响大小为砂带目数>进给量>砂带线速度>横向进给速度。对MRD影响大小为进给量>砂带目数>砂带线速度>横向进给速度。方差分析得到砂带目数对表面粗糙度的影响高度显著,工件进给量对MRD的影响高度显著。并且两者的影响强度都有减弱的趋势。综合考虑实验指标得到最佳工艺参数组合,并通过正交实验数据建立具有可靠预测效果的多元线性回归模型。4 优化分析及预测模型
4.1 优化分析

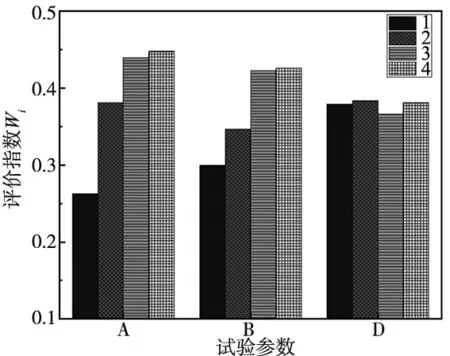
4.2 回归预测模型

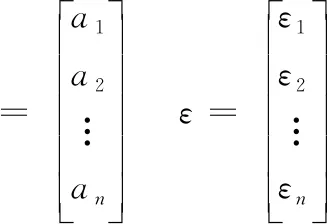

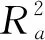
5 结论

