基于无网格法的微生物驱数值模拟

曹琳，修建龙，黄立信，黄峰，徐云峰，赵辉，盛广龙

（1.中国科学院大学，北京 100049；2.中国科学院渗流流体力学研究所，河北廊坊 065007；3.中国石油勘探开发研究院，北京 100083；4.中国石油新疆油田分公司重油开发公司，新疆克拉玛依 834000；5.长江大学石油工程学院，武汉 430100）

经历了传统的一次采油和二次采油之后，油藏中仍然有大约2/3 的原油剩余[1-3]。现有提高采收率技术中，微生物驱提高采收率技术是一项施工简单、费用低廉、安全环保、不伤害油层、返排液无需处理、潜力巨大的三次采油技术[4]。微生物驱是利用微生物及其代谢产物作用于油层，降低原油黏度和油水界面张力，从而提高油藏中原油的流动性，最终提高采收率[5-6]。目前，微生物驱机理研究主要采用室内实验结合数值模拟的方法。室内实验方面，文献［7］进行了微生物驱室内实验，引入了微生物因子对残余油饱和度的影响。文献［8］通过实验研究数据，拟合出微生物质量浓度与原油黏度之间的关系，并以此建立了微生物降黏模型。室内实验模拟可以较为真实地反映地下微生物驱机理，然而由于实验耗时长、成本高，很难应用到实际生产井模拟分析。为此，学者们普遍采用数值模拟进行微生物驱模拟，文献［9］基于菌体流动及吸附实验，发现采油过程中，微生物在多孔介质运移中筛分作用比吸附作用更加突出，进而完善了微生物运移数学模型；文献［10］分析了微生物质量浓度、营养液质量浓度、段塞结构、油层渗透率等因素对驱油效率的影响，并采用全隐式有限差分法对其所建立数学模型进行求解。微生物驱机理的研究已经相对完善，但是在微生物驱数学模型的求解上，主要采用的是有限差分法，此类方法以网格划分为前提，在计算过程中经常需要进行网格重构，势必会对计算速度产生较大影响，同时此方法前后处理也比较麻烦。

1977 年，文献［11］在解决无边界天体物理问题时提出了无网格法，其本质是利用一组散布在问题域及域边界上的节点，构造场函数近似表达式的一种计算方法。文献［12］用伽辽金无网格法对单相稳定渗流问题进行了研究，研究结果表明，无网格法无需划分网格，能够消除划分网格所带来的困难，解决许多基于网格方法不能解决的问题。文献［13］针对油水两相油藏渗流问题，分析伽辽金无网格法和加权最小二乘无网格法的基本原理，并将无网格法引入到数值试井中，建立复杂断块油藏油水两相无网格试井解释模型。大量基于无网格法的研究表明，无网格法在计算中完全脱离了网格，前处理工作相对于有限差分法简单了许多[14-16]。加权最小二乘无网格法直接使用最小二乘法建立系统的变分原理，消除了控制方程在边界节点处的残差，无需进行GAUSS积分，计算量小。

由于微生物驱机理复杂，涉及组分相对较多，使用有限差分法等数值模拟方法求解时存在计算不稳定、计算效率低的缺点[17]。本文将无网格法拓展到微生物驱数值模拟中，通过考虑微生物生长/死亡、营养消耗、产物生成、化学趋向性、对流扩散、吸附、解吸等物理化学过程，建立了微生物驱提高采收率数学模型，采用加权最小二乘无网格法进行了求解，分析无网格法在微生物驱数值模拟中的应用效果。

1 数学模型的建立与求解

1.1 微生物驱物理模型

本文通过构建一注一采的一维油藏模型进行微生物驱机理研究（图1）。图中W1 井为注水井，P1 井为采油井，采用均匀布点，序号为节点数。

图1 微生物驱物理模型Fig.1.Physical model of microbial flooding

模型基本假设条件：①油藏均质且储集层内流体为油、水两相；②油、水是微可压缩流体，流体混合无体积变化；③油藏等温；④微生物及其营养物和代谢产物均只溶于水相中。

1.2 微生物驱数学模型

为定量描述微生物驱这一过程，建立的微生物驱数学模型不仅需要考虑渗流场中油和水的运移，而且还需包含微生物及其营养物和代谢产物的运移。渗流场中的油、水流动方程满足达西定律和质量守恒定律，其加权最小二乘无网格法的计算形式可参考文献［18］。

考虑微生物及其营养物和代谢产物的对流、扩散、吸附、解吸、沉淀等作用，结合微生物反应动力学，微生物及其营养物和代谢产物的运移方程[19]为

假定井以定产量进行生产，设定初始含水饱和度，该模型能够通过设置不同条件来模拟外源和内源微生物驱，其区别在于油藏原始微生物质量浓度是否为0。对于边界条件，生物场的质量浓度边界条件均设为注入常数。随着微生物的生长和繁殖，油藏渗透率、原油黏度和相对渗透率会随之发生改变，同时这些物性参数的变化也反映出微生物驱机理。

1.3 无网格法求解

加权残量法可作为无网格法的理论基础，本文应用移动最小二乘法来构造近似函数，然后利用最小二乘法对控制方程进行离散，建立对应的无网格法，即加权最小二乘无网格法。

1.3.1 移动最小二乘法

设在求解域Ω内有场函数u（x）以及一组随机分布的离散节点xj（j=1，2，…，n），用Ωj表示节点xj的影响域，在二维问题中，影响域常取作圆形或矩形。使用移动最小二乘法进行全局近似，求解域内的任意节点x有近似函数：

权函数是移动最小二乘法近似中的重要组成部分，没有理论上的具体规则，带有任意性，一般满足权函数ω（r）非负，r=dj/dmj，dj=︱x-xj︱，dmj是xj的影响域半径，本文中影响域半径取dmj=scale×s［1］，s［1］为节点xj与距其最近的节点距离，scale为大于等于1的乘子。

最小二乘法能够用来求解具有任何类型的偏微分方程，从变分原理和加权残量法上讲这类方法是来建立泛函的，且其权函数或称为检验函数就是残量本身。首先，令ΠΩ=再取最小值，即对边界条件运用更为简单、有效的本质边界条件处理方案即罚函数法。罚函数的功能，是对非可行点或企图穿越边界而逃离可行域的点赋予一个极大值，即将有约束最优化问题转化为无约束最优化问题。

对具体问题采用上述基于移动最小二乘法的近似函数，并采用上述积分格式的离散点求和形式便得到了加权最小二乘无网格法[20]。

1.3.2 加权最小二乘无网格法求解微生物驱

设求解域Ω及边界Γ内有n个离散节点，营养物质量浓度近似函数通过移动最小二乘法来进行全局近似，如下式：

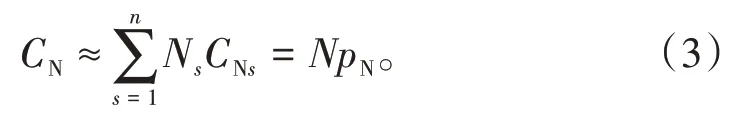
其中，N=[N1(x)N2(x)…Nn(x)]为形函数；pN=[CN1CN2…CNn]T为营养物质量浓度分布的矩阵形式。

将（3）式代入（1）式中，可得营养物运移方程的残量方程：

因此营养物运移方程的加权平方和公式为

将（5）式取最小值，即：

上式通常需要写成离散形式，即：

其中，n1为第一类边界条件Γ上的节点总数，δRN为残量方程RN的变分形式，写成矩阵形式如下：

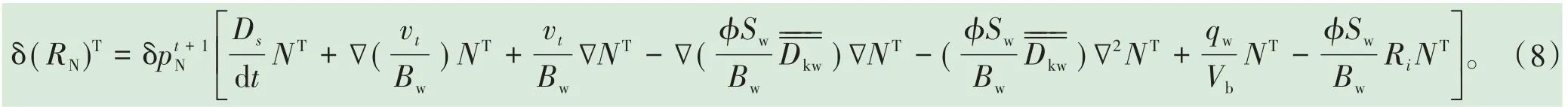
其中，

（10）式求出下一时刻微生物质量浓度后，代谢产物质量浓度变化速率如下式：

代谢产物运移方程的加权最小二乘无网格法求解方法与求解营养物和微生物类似，这里不再累述。

2 算例分析

基于上文建立的加权最小二乘无网格法求解微生物驱数学模型，并拓展到二维问题的求解上，设计了如下算例，算例井网布置采用一注四采模型（图2）。W1为注水井，P1井、P2井、P3井和P4井为采油井。正方形油藏边长为100 m，层厚为40 m，渗透率为100 mD，孔隙度为20%。把方形油藏用9×9 个节点进行离散，应用加权最小二乘无网格法进行求解，节点影响域中的scale 为3，选用GAUSS 权函数和二次基函数，时间步长取Δt=1 d，生产制度注采均为47.67 m3/d。本文模型与文献［19］建立的模型中驱油机理大致相同，物性参数如表1所示。

本文算例采用如下生产制度：在注入井一次注水1.65 PV 至含水率95%，后续以连续注入的方式注入0.30 PV 营养物和微生物的混合溶液（营养物质量浓度为2.495 mg/mL，微生物质量浓度为1.275 mg/mL），最终水驱至含水率98%，微生物菌体在多孔介质中持续吸收营养物，生长、繁殖并代谢出相关产物，随着注入的持续进行，代谢产物的分布会发生变化。

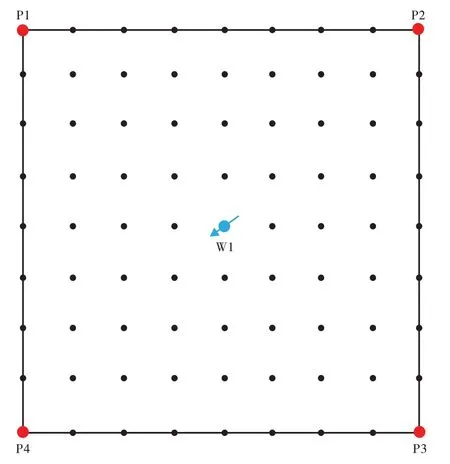
图2 一注四采模型与节点布置Fig.2.Model with one injection well and four producing wells,and deployment of mesh points

表1 加权最小二乘无网格法求解微生物驱数学模型物性参数[19-21]Table 1.Physical parameters of the mathematical model for microbial flooding solved by the weighted least square meshless method[19-21]

为了验证本文方法的正确性与计算效率，将上述算例计算结果与有限差分法进行比较。有限差分法计算所用参数和本文所用参数保持一致，采用12.5 m×12.5 m×40.0 m 的网格作为单个计算单元。两者计算所得到的代谢产物质量浓度分布如图3 所示，含水率变化与采收率变化曲线如图4 所示，加权最小二乘无网格法与有限差分法的计算结果基本吻合，说明了本方法的正确性与有效性。在加权最小二乘无网格法求解的节点单元数比有限差分法求解的要多15 个的情况下，计算效率反而提高了62%。在总注入量为1.66 PV 时，油藏中营养物和微生物混合溶液比较少，产生的代谢产物也少，主要集中在注入井附近。当总注入量为1.95 PV 时，营养物和微生物混合溶液停止注入，进入后续水驱阶段后，油藏中的微生物菌体因得不到相应的营养物，也将停止产生代谢产物。随着后续水驱阶段的进行，代谢产物质量浓度峰值也逐步向采出端移动，且代谢产物质量浓度峰值也因吸附作用而逐渐下降。

图3 营养物和微生物混合溶液不同注入量下代谢产物质量浓度对比Fig.3.Mass concentration of metabolites at different injected volumes of the mixed solution of nutrient and microorganism

图4 微生物驱和水驱的含水率变化曲线（a）和采收率变化曲线（b）Fig.4.(a)Water cut curves and(b)recovery curves of microbial flooding and water flooding

3 无网格法敏感性分析

在上述理论和求解方法的基础之上，对影响无网格法计算精度和计算效率的布点方案、节点影响域和权函数分别进行参数敏感性分析，进而验证该方法在微生物驱数值模拟求解中的正确性。

3.1 不同布点密度分析

应用加权最小二乘无网格法求解时，选择合适的布点方案非常重要。本文采用等距离均匀分布，在正方形油藏区域100 m×100 m，选用了6×6、9×9、21×21和51×51 的布点方案，节点影响域中的scale 为3，权函数公式为GAUSS 函数，进行微生物驱数学模型的计算，并将计算结果和有限差分法计算结果作对比。51×51 布点方案的计算精度与有限差分法最接近，但是当布点数下降时，误差并没有大幅增加（图5）。但布点密的方案所需的计算时间明显高于布点稀疏的方案，如51×51布点方案的计算时间大约是9×9布点方案的10倍，分别是53.0 s和5.3 s。而9×9 布点方案和6×6布点方案的计算时间却基本相同。由此可见，求解微生物驱模型时，在没有大幅降低计算精度的情况下，每100 m×100 m的油藏区域采用9×9 的布点密度能大幅度提升计算效率。

3.2 不同的节点影响域分析

图5 微生物驱不同布点方案含水率变化曲线Fig.5.Water cut curves of different meshing schemes for microbial flooding

加权最小二乘无网格法自身具有较高的精度，但其结果还依赖于节点影响域的选取。其参数最优值和所求解的具体问题有关，因此本文选取节点影响域中的scale 为2、3、4 和5，对微生物驱数学模型求解进行了验证分析。从图6 中能够看出随着节点影响域的减小，计算精度呈现先增加后降低的趋势，在scale为3 时，计算精度最高。对计算效率分析发现，节点影响域对计算效率并没有太大影响，运行时间为5.5 s左右，而有限差分法运行时间为13.8 s。因此本文选用scale为3来对微生物驱数学模型进行求解，以确保求解的正确性。

图6 微生物驱不同节点影响域含水率分布Fig.6.Water cut distribution in the influence domain of different points

3.3 不同的权函数分析

不同的权函数能使节点在其影响域里所产生的影响随权函数不同而改变，其对最终结果的精确度也会产生一定影响。本文对微生物驱模型选用了不同的权函数，选用9×9 的布点方案，影响域中的scale为3，权函数分别用SPLIN、GAUSS、CUBIC 和CSRBF。从图7中可以看出，采用GAUSS权函数的最终结果精确度最高，说明这种权函数分布最适合于微生物驱数学模型的求解。

图7 微生物驱不同权函数计算含水率变化曲线Fig.7.Variations of water cut with different weight functions in the microbial flooding model

4 结论

（1）将无网格法引入微生物驱数学模型求解，考虑对流、扩散、微生物繁殖和死亡、生物趋化性、营养物消耗、代谢产物生成、吸附等特性，建立了微生物提高采收率数学模型，采用无网格法对渗流场和生物场进行了求解。

（2）将无网格法与有限差分法求解微生物驱数学模型进行了对比验证，结果表明，在确保计算正确性的前提下，无网格法计算效率明显优于有限差分法。

（3）对影响无网格法计算精度和计算效率的参数进行了敏感性分析，得出在边长为100 m 方形油藏区域采用9×9 均匀布点方案，影响域为3 倍节点间距为半径的圆形和GAUSS 权函数时，更适用于微生物驱数学模型的求解，能在确保计算正确性的前提下，提高计算的效率。

符号注释

aN、bN——营养物的吸附常数；

A——菌体维持生命时代谢产物的生成速率，1/d；

B——组分代谢产物得率，g/g；

Bw——地层体积系数；

Ci、Cis——分别为水相和吸附相中各组分的质量浓度，g/L；

CN、CNs——分别为营养物质量浓度和第s个点的营养物质量浓度，g/L；

dj——xj点到x点的距离，m；

dmj——影响域半径，m；

Dm——微生物在水相中的扩散系数，m2/d；

i——N（营养物）、m（微生物）和d（代谢产物）；

kc——微生物的化学趋向系数，m2/d；

N——无网格法中的形函数；

qw——日注入量（采出量），m3；

R2——代谢产物质量浓度变化速率，g/d；

Rd——组分脱附速率，g/L；

Ri——组分变化速率，g/L；

RN、Rm——分别为营养物和微生物控制方程的残量方程；

Rr——组分吸附速率，g/L；

RΩ——任意控制方程在求解域内的产量方程；

s——无网格法中代表节点；

Sw——含水饱和度；

t——时间，d；

Δt——时间步长，d；

u——局部最佳近似；

vt——流速，m/s；

Vb——源汇处岩石孔隙体积，m3；

α——罚函数；

φ——孔隙度；

Γ——控制方程的边界条件。