高压压气机出口级叶型加工偏差特征及其影响
刘佳鑫,于贤君,2,*,孟德君,史文斌,刘宝杰,2
1. 北京航空航天大学 能源与动力工程学院,北京 100083 2. 北京航空航天大学 航空发动机研究院,北京 100083 3. 中国航发沈阳发动机研究所,沈阳 110015
压气机是航空燃气涡轮发动机的三大部件之一,不但对于发动机的推力和耗油率等性能至关重要,而且对于发动机的重量和制造成本等也有重要影响。随着对航空发动机性能需求的不断提高,迫切需要进一步提高压气机的效率和裕度性能水平。压气机叶片在实际的制造和运行过程中,由于制造误差或侵蚀磨损难免会出现一定的几何偏差[1-2]。叶片的几何偏差对压气机性能以及加工和维护成本都有着不可忽视的影响。因此,为了进一步提高压气机的效率和裕度等性能水平及其工作的鲁棒性,叶型的气动性能对几何偏差的敏感性问题逐渐得到了国内外研究者的广泛关注。
从20世纪80年代开始,国外的研究者就已经对压气机的几何偏差问题展开了研究[3-4]。随着研究的深入,Suder等用实验证明了叶片的前10%弦长区域对几何偏差和表面粗糙度都较为敏感[5]。在此基础上Elmstrom等利用涂层进一步展开了对叶型前缘形状对性能影响的量化研究[6],研究表明叶型前缘的厚度或形状对叶型的气动性能起主导作用。为了获取压气机的几何偏差数据模型,以Garzon[7-9]为代表的研究者采用主成分分析法(Principle Component Analysis, PCA)对风扇[10]和压气机[8]的几何偏差进行了不确定度建模。在此基础上,大量学者利用蒙特卡洛法[11]、伴随方法[12]以及多项式混沌法[13]等不确定性分析方法对压气机的气动不确定性进行了研究,并致力于发展对几何偏差不敏感的叶型鲁棒性设计和优化方法[14]。Goodhand等则对前缘形状不同的叶型对几何偏差的敏感程度和流动机理进行了研究,并以此发展出了降低前缘敏感性的鲁棒性设计方法[15-16]。
2000年以来,国内对几何偏差的影响也展开了系统深入的研究。张伟昊等的研究表明,叶型的加工和装配误差对整个涡轮部件甚至整机性能都有显著的影响[17-18]。高丽敏等结合实际加工偏差,针对叶片的扭转角和弦长等偏差对叶型气动性能的影响趋势[19]、加工误差的不确定性分析[20]以及加工误差在三维动叶中的影响进行了系统地分析[21]并开展了鲁棒性设计[22-23]的相关研究。罗佳奇[12,24]和郑新前[25]等分别采用伴随方法和代理模型方法发展了对几何偏差导致的叶型性能变化的快速预测或优化方法。
可以看出,在几何偏差影响方面,国内外学者对各种形式的加工偏差的影响机理、敏感性分析、不确定性分析方法发展以及叶型和叶片的鲁棒性设计方法发展等都已经开展了系统全面的研究。考虑到加工偏差与加工工艺密切相关,并且在工程实际中小批量试制和大批量生产之间的工艺稳定性也会有所区别。因此,结合工程实际中批量生产的产品逆向数据,分析加工偏差的特征及其影响,可为发展有针对性的鲁棒性气动设计和产品工艺优化设计方法提供必要的支持。
基于一组批量生产发动机产品的100套高压压气机叶片逆向测量数据,通过对叶型的实际加工偏差进行统计分析,得到了其主要偏差特征,并提出了偏差特征的分解定义方法。然后基于所得到的真实加工叶型数据,进行了所有叶型的气动性能计算分析,确定了真实叶型的气动特性与理论叶型气动特性的偏差规律,并对叶型不同典型区域的真实加工偏差状态对叶型气动性能的影响机理进行了分析。
1 工程实际加工叶型的几何特征
1.1 实际加工叶型与基准叶型对比
研究对象为某高压压气机出口级转子,此处的叶片主要采用五坐标加工中心加工而成,最后采用抛光和振动光饰等工艺提高叶表的光洁度,实际测量叶片不少于100套。测量叶片直接来源于验收合格的压气机叶片,在一定程度上反映了国内高压压气机后面级叶型的加工水平。论文重点分析的是叶中基元(进口马赫数Ma=0.5,雷诺数Re=1.0×106,湍流度Tu=4%),为典型的亚声多圆弧叶型。所有叶型的逆向测量数据如图1所示,其中的红色曲线是基准理论叶型,黑色曲线为实际加工叶型,绿色曲线为实际加工叶型的平均叶型。
如图1所示,叶中基元的加工偏差偏向正偏差,前尾缘的加工偏差相对较大。从平均叶型与基准叶型的对比可以看出,实际叶型存在前缘向吸力面偏移的系统性偏差,而这样的系统性偏差会使前尾缘的几何角发生一定的改变。同时存在一定数量的加工偏差明显大于其他叶型的粗大偏差样本。
基于上面的定性分析可知,当前实际叶型的加工偏差存在系统性偏差。下面将采用统计分析的方法,对该叶型的加工特点进行统计分析,以确定该叶型实际加工后的几何不确定度特征。

图1 高压压气机出口级转子叶中基元的基准叶型(红色)、实际加工叶型(黑色)以及平均叶型(绿色)Fig.1 Datum blade (red), manufactured blades (black) and mean blade (green) of mid-height section from high pressure compressor rotor outlet stage
1.2 关键几何参数定义
通过大量的分析表明,不同的偏差形式对叶型的几何特征和气动性能的影响不同。结合文献[26]的偏差定义标准以及气动设计过程中的造型设计控制参数,加工偏差总体上可分为两类:一类为整体偏差,即表征描述叶型特征几何形状的宏观控制参数的偏差,包括叶型的弦长、进出口几何角和安装角等;另一类为局部偏差,定义为叶型局部区域内叶型型面相对于基准叶型的偏差,由轮廓度和轮廓度变化率等参数来表征。整体偏差和局部偏差在大多数情况下相对独立,因此有必要分开进行分析,便于对偏差进行更加细致的解析并探究其影响机理;但是在前尾缘处的局部偏差会与整体偏差参数存在一定耦合,需要在分析中引起注意,在本文中将详细论述。
基于文献[26],衡量加工偏差的两个重要指标为轮廓度和轮廓度变化率,其定义为
轮廓度:基准叶型表面法线方向与实际叶型对应点之间的距离,实际叶型的坐标点在基准叶型外则为正,反之则为负。
轮廓度变化率:轮廓度变化率是衡量偏差的波纹度的指标,即任意两个相同方向的局部叶型偏差轮廓度的差值或任意两个相异方向的局部叶型偏差轮廓度的和与其对应的理想叶型上的两点间的型线长度之比。当两点间的型线长度趋于0时,偏差的轮廓度变化率即为轮廓度的一阶导数。
1.3 加工偏差统计特征分析
1.3.1 偏差的统计收敛性
由于所分析的数据属于有限样本,有必要确定各个特征参数统计结果的收敛性[27]。图2给出了典型参数的平均值和方差收敛性结果。可以看出,平均值统计结果在大于40个样本后变化就已经很小,而方差结果中除了出口几何角偏差统计结果收敛性稍差外,其他参数也与平均值结果的统计规律类似。对于出口几何角的方差统计收敛性,在大于40个统计样本之后,方差值的变化在收敛值的±0.1°以内,对分析结果没有影响。因此,本文采用100个有限样本进行统计分析,并探讨其对叶型气动性能影响的机理具有较好的可行性。
1.3.2 局部几何偏差特征

图2 不同特征参数的加工偏差值统计收敛特性Fig.2 Statistical convergence characteristics of representative geometry parameters for manufacture deviations
根据叶型加工偏差统计结果,在叶表不同区域偏差分布具有不同的特征,受篇幅限制,论文给出了几个典型的但能够表征偏差在叶表总体分布特征的点上的加工偏差统计分析结果,相关特征点的定义如图3所示。将叶表按照吸力面和压力面弧长做归一化处理,其中吸力面的尾缘点为-1, 吸力面(压力面)前缘点为0,压力面尾缘点为1(与-1重合)。下面给出了1(图4)、-0.5(图5)、0.5(图6)和0(图7)4个典型位置的局部几何偏差特征统计结果,分别代表尾缘附近区域、吸力面叶身主体区域、压力面叶身主体区域和前缘附近区域的加工偏差特征。

图3 用于局部偏差统计分析的叶表特征点定义Fig.3 Definition of representative points on blade surface for geometry deviation statistical analyses
图4为尾缘处局部偏差的轮廓度和轮廓度变化率的统计结果。从图中可以看出,尾缘点的加工偏差轮廓度均大于零,说明该叶型的实际加工结果为尾缘偏厚(平均值为0.042 mm,两倍标准差2σ为0.049 mm),同时分布形态近似为正态分布。与图5、图6和图7对比可知,尾缘点的轮廓度和轮廓度变化率平均值(衡量系统性偏差)和两倍标准差2σ(对于正态分布对应了95%的置信度区间[28],本文用此指标衡量不确定度)都相对较大。此外,由于尾缘偏差的轮廓度变化率很大且平均值不为0,会出现局部偏差与出口几何角偏差耦合现象,图1所示的结果也显示出了这种趋势。

图4 实际叶型尾缘特征点的局部偏差统计直方图Fig.4 Histogram of local deviations at feature point on trailing edge of manufactured blades
图5和图6分别为叶身吸力面和压力面的局部偏差统计结果,与图4尾缘点和图7前缘点的统计结果对比可知,叶身吸力面和压力面局部偏差的轮廓度变化率相对较小,与前尾缘相比小了一个数量级,因此叶身的加工偏差对叶型型面的斜率和曲率的改变较小,近似为均匀偏差。同时,叶身吸力面轮廓度平均值明显偏向正偏差(平均值为0.019 mm,2σ为0.039 mm),压力面轮廓度平均值接近0但稍偏向负偏差(平均值为-0.007 mm,2σ为0.038 mm)。此外,还可以看出,吸力面特征点的偏差分布形式接近正态分布(图5),而压力面则有些偏离正态分布(图6),这可能与叶片加工工艺相关。
图7为叶型前缘点的偏差统计结果,可以看出前缘点局部偏差轮廓度的平均值依然偏向正偏差(平均值为0.020 mm,2σ为0.048 mm),且具有较好的正态分布特征。与叶身相比可知,前缘点局部偏差的轮廓度变化率远大于叶身,与前述对尾缘局部偏差的分析可知,轮廓度变化率较大的前缘局部偏差可以明显改变前缘的形状,甚至改变前缘进口几何角,从而与整体几何偏差出现耦合。从图7(b)所示的轮廓度变化率平均值小于0可以判断进口几何角系统性偏大。

图5 实际叶型吸力面特征点的局部偏差统计直方图Fig.5 Histogram of local deviations at feature point on suction surface of manufactured blades

图6 实际叶型压力面特征点的局部偏差统计直方图Fig.6 Histogram of local deviations at feature point on pressure surface of manufactured blades


图7 实际叶型前缘点的局部偏差统计直方图Fig.7 Histogram of local deviations at leading edge point of manufactured blades
1.3.3 整体几何偏差特征
图8~图10分别给出了实际加工叶型进口几何角、出口几何角和安装角偏差的统计分布结果。可以看出,进出口几何角和安装角都存在一定的系统性偏差。表1为整体偏差的统计数值,其中进口几何角平均向偏大2.65°,出口几何角平均偏大1.47°且不确定度较大,这进一步验证了前面针对前尾缘点局部偏差统计分析得到的结论。此外,还可以看出安装角偏差的平均值和不确定度都相对较小。叶型的进出口几何角和安装角的偏差分布特征都稍有偏离正态分布,总体表现为进口几何角大偏差概率偏高,出口几何角小偏差概率偏高,安装角偏小的概率稍大。

图8 实际叶型进口几何角偏差统计直方图Fig.8 Histogram of inlet metal angle deviations of manufactured blades

图9 实际叶型出口几何角偏差统计直方图Fig.9 Histogram of outlet metal angle deviations of manufactured blades

图10 实际叶型安装角偏差统计直方图Fig.10 Histogram of stagger angle deviations of manufactured blades

表1 实际叶型整体偏差统计数据
2 工程实际加工叶型的气动特征
2.1 计算软件
为了分析工程实际叶型的气动性能与理论性能的偏差特征,并确定几何偏差和气动性能变化的关联,采用数值模拟方法对所有实际叶型和基准叶型以及平均叶型做了变攻角特性计算。采用的叶型流动数值分析工具是在科学研究和工程应用中被广泛使用的MIT发展的准三维程序MISES。该程序在亚声速压气机、跨声速压气机和跨声速前缘流动中与实验数据进行了广泛的对比校验,表现出了较好的计算可靠性和较高的计算速度[28-31],其计算精度得到了广泛的验证[32-33]并应用于几何偏差问题的研究中[14-15,34]。计算网格设置如表2和图11所示。图12为针对不同前缘微小几何差别叶型的MISES计算结果和实验结果的对比[35],可以看出MISES可以较好地模拟微小几何差别对叶表流动细节的影响。
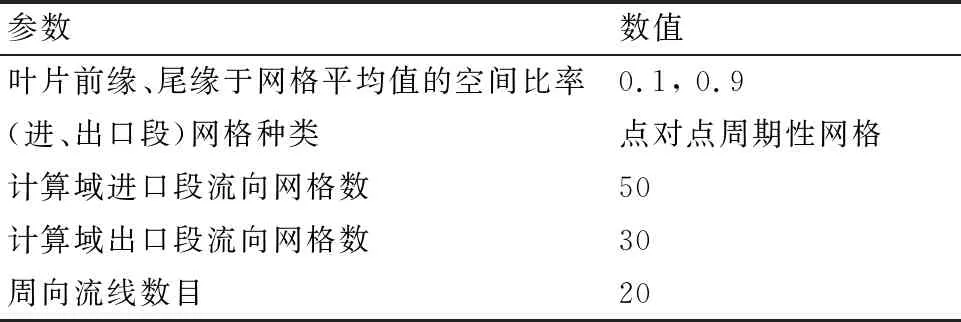
表2 MISES网格参数Table 2 MISES grid parameters

图11 MISES计算网格Fig.11 MISES computational grid

图12 叶表和前缘局部静压升系数分布对比Fig.12 Comparison of local static pressure coefficient distribution on blade surface and near leading edge region
2.2 实际加工叶型气动特征
计算得到的所有叶型的攻角-损失和攻角-落后角特性结果如图13所示,其统计分析结果如表3所示。其中叶型损失ω的定义见式(1)。落后角定义为出口气流角减去基准叶型出口几何角,正负可用攻角范围由基准叶型最小损失的1.5倍确定[15]。
(1)

可以看出,加工偏差对叶型的损失和落后角特性都有较大的影响。在正攻角状态下实际叶型的损失和落后角相对于基准叶型有较大的系统性偏差,实际叶型的正攻角范围平均值比基准叶型小1.10°,正攻角状态下的落后角平均值比基准叶型大0.74°。实际叶型的损失和落后角在整个工作范围内均有较大的不确定度。
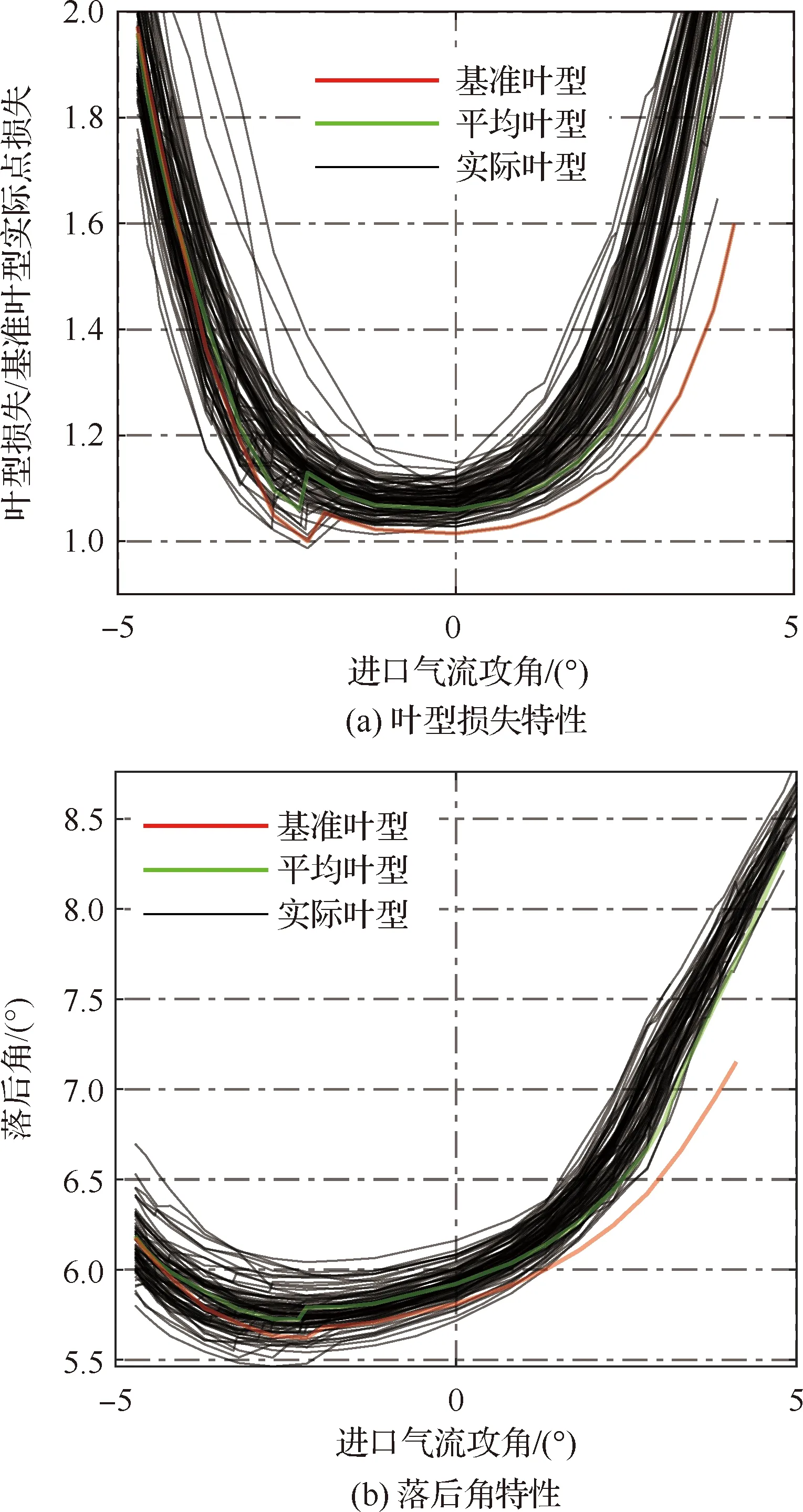
图13 加工偏差对实际叶型气动特性的影响Fig.13 Effect of manufacture deviations on aerodynamic performance of manufactured blades

表3 实际叶型气动性能偏差统计数据
由图13所示,对比实际叶型和平均叶型的气动性能,平均叶型的气动性能在负攻角状态和设计状态附近能较好地反映实际叶型中间值状态的气动性能,但在正攻角状态却不具备这样的特征。为了量化该现象,定义均值偏移为实际叶型气动性能的平均值与平均叶型性能的差与两倍标准差之比,该值越小说明平均叶型和实际叶型的平均性能接近,越大说明二者存在明显偏差,如表3所示。可以看出,平均叶型的负攻角范围偏差、负攻角状态落后角偏差和设计状态落后角偏差与真实叶型气动性能的平均值非常接近,均值偏差都在15%以内;最小损失偏差的均值偏移量稍大一些,约为25%;而正攻角范围偏差和正攻角状态落后角偏差的均值偏移量都非常显著,达到了46%以上。
将上述正攻角范围和落后角偏差统计直方图绘制在图14和图15中,可以更为直观地看出平均值偏移现象。正攻角范围和正攻角状态下的落后角的平均值相对于平均叶型的偏差都是偏向使叶型性能恶化的方向。这说明在正攻角状态下,加工偏差对叶型气动性能的影响具有强烈的非线性效应,加工的分散性会将这种影响放大并恶化叶型性能。这说明,只靠偏差轮廓度的平均值不能准确估计叶型的系统性偏差,还有必要适当控制其分散度或者在影响正攻角性能的参数上提高对加工偏差的限制。为了分析上述现象出现的原因,下面将从机理的角度分析加工偏差对叶型性能的影响。

图14 实际叶型正攻角范围偏差统计图Fig.14 Histogram of positive incidence range variations of manufactured blades

图15 实际叶型在正攻角状态下的落后角偏差统计图Fig.15 Histogram of lag angle variations in positive incidence condition of manufactured blades
3 实际加工偏差对叶型性能的影响
3.1 设计状态
图16给出了设计状态基准叶型的叶表等熵马赫数分布以及加工不确定性的影响。其中以由2σ原则确定的95%置信区间来衡量马赫数分布的不确定性,由不确定度的大小可以得知叶表等熵马赫数对几何不确定度的响应程度——即敏感性。从图中可以看到,加工偏差对前10%弧长范围内的叶表等熵马赫数(尤其是对吸力面以及压力面的速度尖峰)的影响较大,对其他区域的影响较小。由于速度尖峰后的快速扩压过程存在较强的逆压梯度,对附面层的发展有较大的影响,因而对叶型的气动性能有较大的影响。
为了衡量前缘附近绕流引起的快速扩压过程,Goodhand和Miller提出了前缘局部绕流的扩散因子Dspike,其定义为[29]
(2)
式中:umax和umin分别为前缘局部绕流的最大和最小速度。
图17为实际叶型与基准叶型Dspike差值的统计分布,可以看出实际叶型的Dspike均大于基准叶型,且实际叶型的Dspike平均值也大于平均叶型的Dspike。这与表3中实际叶型最小损失的平均值大于基准叶型和平均叶型相符。说明在设计状态加工偏差主要通过影响前缘绕流从而对下游的附面层发展产生影响,且有很强的非线性效应。

图16 设计状态基准叶型叶表等熵马赫数分布以及加工不确定度造成的叶表等熵马赫数不确定度Fig.16 Inviscid surface Mach number distribution of datum blade and Mach number variability caused by manufacture variability in design state

图17 设计状态实际叶型前缘吸力峰扩散因子相对基准叶型的偏差统计Fig.17 Histogram of deviations of leading edge spike diffusion factor for manufactured blades away from datum blade in design state
3.2 负攻角状态
如图18所示,在负攻角状态加工偏差对叶表等熵马赫数的影响主要集中在压力面的前20%弧长之前,同时对尾缘附近的叶表等熵马赫数也有一定影响。可以看出加工偏差对压力面峰值马赫数及其减速增压过程有较强影响,同时在吸力面也容易形成较强的吸力峰。图19(a)的压力面附面层形状因子显示,在压力面前20%区域内气流经过急剧的加速和减速产生了局部分离(形状因子H>4)。图19(b)所示的吸力面形状因子表明,基准叶型和平均叶型以及一部分实际叶型在约27%归一化叶表长度之前的H>2.5,附面层处于层流状态。但对于另一部分实际叶型而言,吸力面前缘的吸力峰增强导致了前缘附近的形状因子迅速增加后急剧减小,即转捩点提前到了前缘附近,增加了叶型损失。

图18 负攻角状态基准叶型叶表等熵马赫数分布以及加工不确定度造成的叶表等熵马赫数不确定度Fig.18 Inviscid surface Mach number distribution of datum blade and Mach number variability caused by manufacture variability in negative state
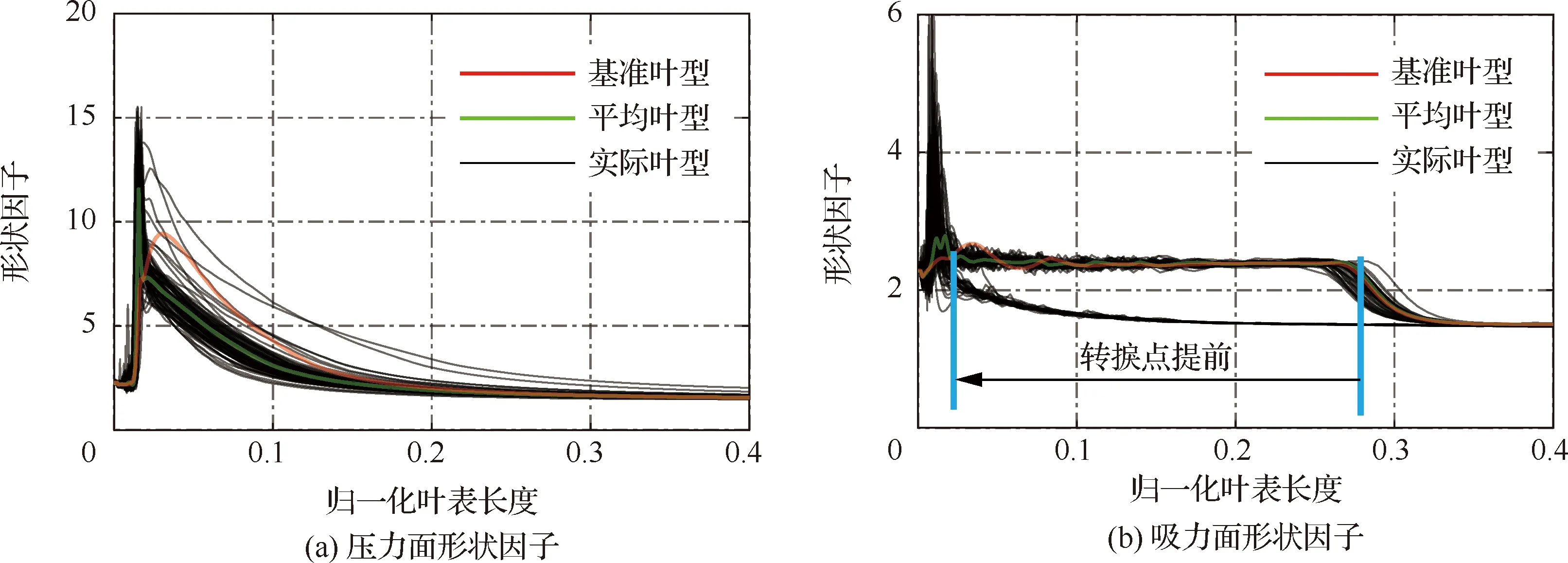
图19 负攻角状态下基准叶型和实际叶型的附面层形状因子Fig.19 Boundary layer shape factor of datum and manufactured blades in negative state
从图20所示的动量厚度分布可以得知,局部分离区域的范围和状态极大地影响了下游附面层的发展,附面层的增厚/变薄则可以影响对应状态的叶型损失,尾缘处的附面层变化则可以体现落后角的变化。可以看出,局部分离区域附近的几何偏差对叶型的负攻角范围和对应的落后角都有显著的影响。

图20 负攻角状态下基准叶型和实际叶型的 附面层动量厚度Fig.20 Boundary layer momentum thickness of datum and manufactured blades in negative state
3.3 正攻角状态
如图21所示,正攻角状态几何偏差对叶表等熵马赫数不确定性的影响主要集中在吸力面前10%弧长区域,在这个区域内加工偏差对叶表等熵马赫数的最大值和其后的减速过程有较大的影响。此外,还可以看出,由于前缘加工偏差的影响整个叶表的等熵马赫数分布与基准叶型相比都出现了明显偏差,尤其是在近尾缘20%弦长区域内的偏差十分明显。这一方面是由前缘敏感区的强非线性影响导致的,另外也可能是与其他区域的偏差耦合导致的,这将在后面做进一步深入分析。
图22给出了实际叶型吸力面叶表等熵马赫数的最大值与基准叶型的偏差,可以看出绝大部分实际叶型的吸力面最大马赫数都大于基准叶型。
图23给出了吸力面的形状因子分布,可以看出在前缘附近实际叶型的形状因子峰值普遍大于基准叶型,这导致了吸力面的局部分离更加严重,从而造成了图24中的实际叶型动量厚度在局部分离区后大幅增加。这不仅会导致叶型损失增加,也导致吸力面尾缘处动量厚度和落后角的增大。虽然图22中平均叶型的叶表等熵马赫数最大值与实际叶型最大马赫数的平均值相近,但从图23可以看出,实际叶型造成的局部分离普遍大于平均叶型,因此实际叶型吸力面的动量厚度也普遍大于平均叶型,如图24所示。与负攻角状态类似,正攻角状态加工偏差对前缘速度峰值以及其后的减速过程有明显的影响,当存在局部分离现象时,这种影响会更加显著。

图21 正攻角状态基准叶型叶表等熵马赫数分布以及加工不确定度造成的叶表等熵马赫数不确定度Fig.21 Inviscid surface Mach number distribution of datum blade and Mach number variability caused by manufacture variability in positive state

图22 正攻角状态下实际叶型吸力面最大马赫数相对基准叶型的偏差统计Fig.22 Histogram of max Mach number variations on suction surface of manufactured blades from datum blade in positive state
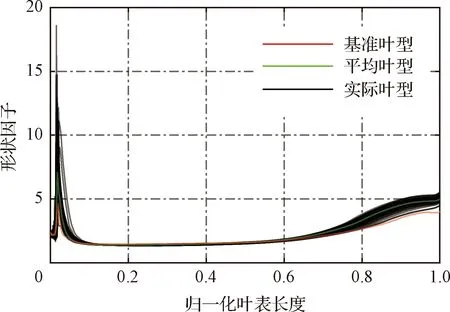
图23 正攻角状态下基准叶型和实际叶型的吸力面附面层形状因子Fig.23 Boundary layer shape factor on suction surfaces of datum and manufactured blades in positive state

图24 正攻角状态基准叶型和实际叶型的叶表 附面层动量厚度Fig.24 Boundary layer momentum thickness on datum and manufactured blades in positive state
4 加工偏差影响的机理分析
由前面的分析不难看出,对于实际的加工叶型,敏感区主要集中在前缘附近,而叶身和尾缘的情况较为一致并且都不太敏感。因此,本部分将分别从前缘和叶身加工偏差影响开展机理分析,其中叶身的相关分析也适用于尾缘区域。
4.1 前缘加工偏差的影响
为了进行更深入的加工偏差影响机理分析,首先将前缘加工偏差独立出来开展分析。将实际加工偏差的前10%弦长部分保留,而叶身部分的偏差设为0,前缘与叶身之间在10%~30%弦长范围内平滑过渡。图25显示了直观的分解示意。
图26为仅保留实际前缘偏差的叶型的损失和落后角特性。与图13所示结果对比可知,前缘偏差是叶型性能影响的主要因素,这与上文中得到的结论相符。但与图13不同的是,前缘偏差在负攻角状态依然产生了一定的系统性偏差,对设计点损失和落后角的影响也比实际情况偏小。
由于叶型性能的系统性偏差直接关系到压气机性能的系统性偏差,需要尤为关注。基于前面的分析可知,前缘局部偏差与叶型进口几何角的整体偏差存在耦合关系。一般认为在不改变整体几何状态的情况下,局部偏差应该仅会影响性能的分散度,也就是不确定度,而系统性偏差应该由整体几何偏差造成。于贤君等的研究表明[36],前缘的“偏头”偏差(即进口几何角偏差)对叶型攻角范围的影响较大。为了进一步验证以上推论,通过改变基准叶型前12%弦长范围内中弧线分布的方式分析进口几何角偏差对叶型性能的影响规律。图27为进口几何角偏差叶型与基准叶型的对比示意图。图28为进口几何角偏差为4.4°的轮廓度示意图。值得注意的是,当进口几何角偏差在-3.7°与4.4°之间时,轮廓度在-0.042 mm与0.036 mm之间,处于加工公差带范围内,这说明只靠轮廓度公差带很难限制进口几何角偏差。
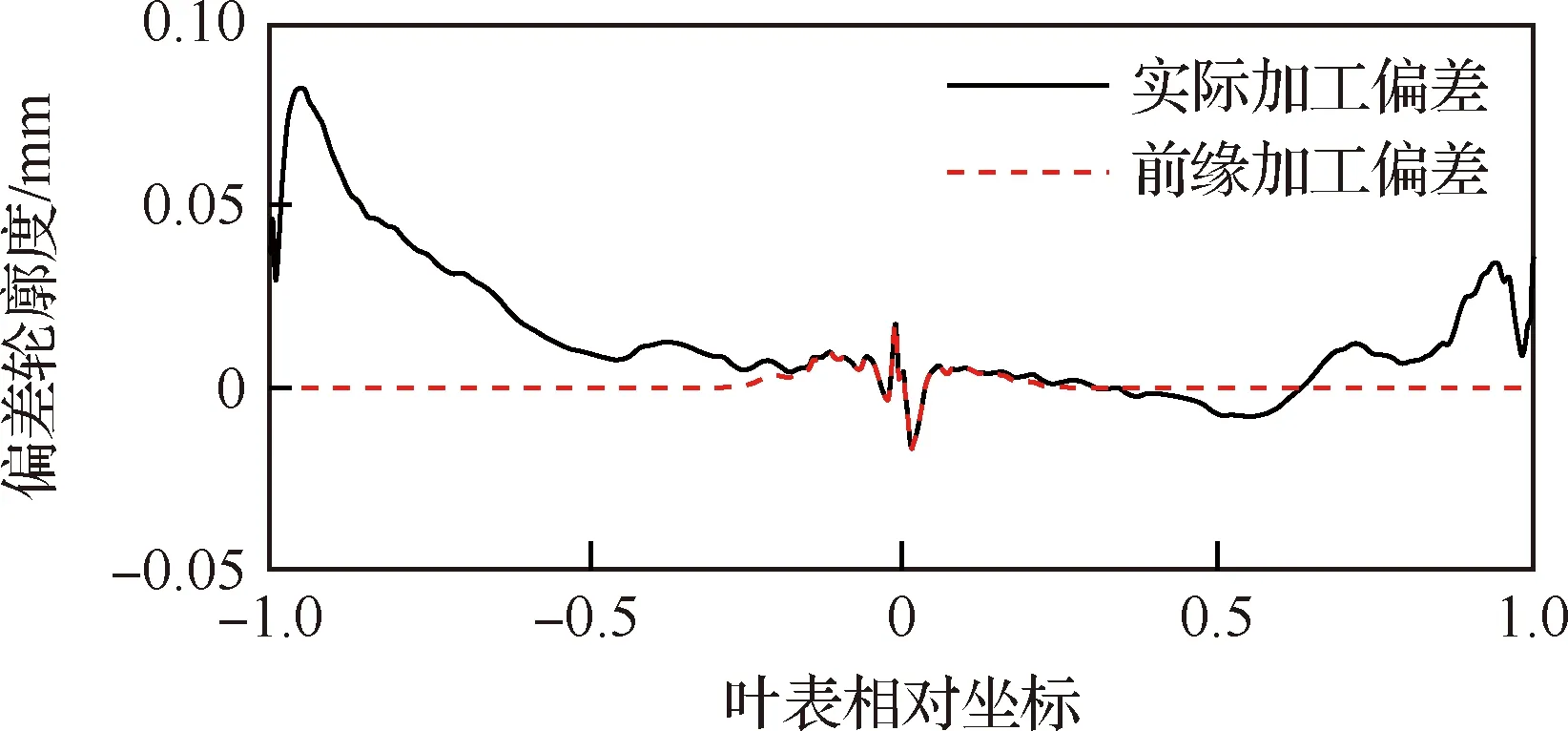
图25 实际加工偏差与前缘加工偏差示意图Fig.25 Diagram of manufacture deviation and leading edge manufacture deviation
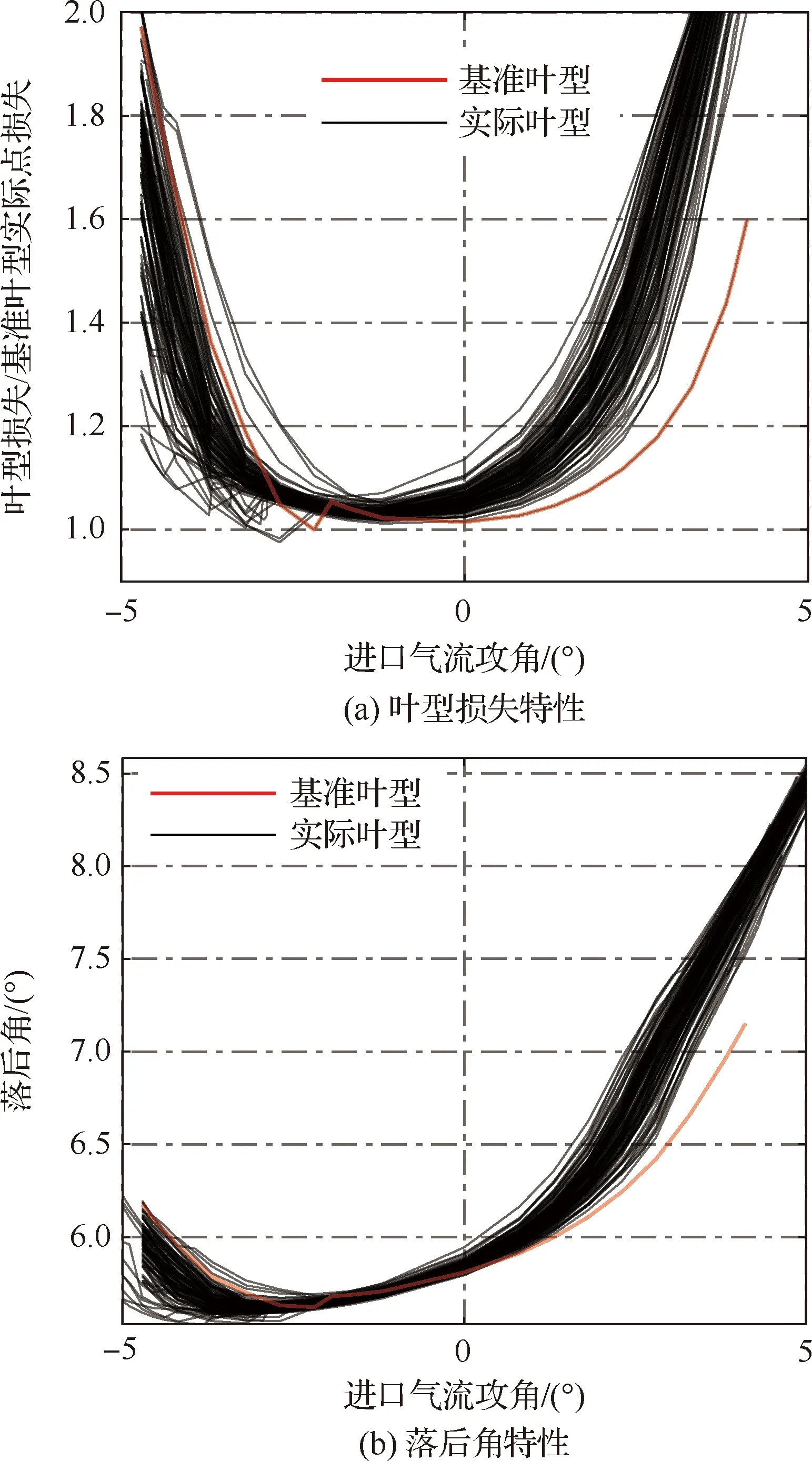
图26 前缘加工偏差对叶型气动特性的影响Fig.26 Effect of leading edge manufacture deviations on blade aerodynamic performance

图27 基准叶型和进口几何角偏差叶型对比Fig.27 Comparison between datum blade and blade with inlet geometric angle deviation

图28 进口几何角偏差轮廓度示意图Fig.28 Diagram of profile tolerance of inlet geometric angle deviation
图29为进口几何角偏差在-3.7°~4.4°之间的偏差叶型计算所得的特性图。如图所示,进口几何角偏差对正攻角和负攻角状态的叶型损失和落后角影响都较大,对零攻角状态叶型损失和落后角的影响较小;进口几何角偏差带来的负攻角状态下的叶型损失和落后角不确定性要大于正攻角状态。此外,还可以发现,对于进口几何角偏差为正值的状态(与前面实际加工偏差特征相似),叶型的特性线会向左偏移,即适当改善了负攻角特性,但是显著恶化了正攻角特性,这与前面将真实的前缘偏差独立出来计算分析得到的结果一致。这证明了真实加工偏差中的进口几何角偏差是导致叶型性能出现系统性偏差的原因。

图29 进口几何角偏差对叶型气动特性的影响Fig.29 Effect of inlet geometric angle deviations on blade aerodynamic performance
图30给出了定量分析进口几何角偏差对叶型性能影响的结果,可以看出改变进口几何角对负攻角范围和负攻角状态下的落后角的影响规律都近似线性关系,而对正攻角范围的影响略偏离线性特征,对正攻角状态下的落后角的影响则表现出了强烈的非线性特征。这也与前面分析的实际前缘加工偏差的影响规律相符。
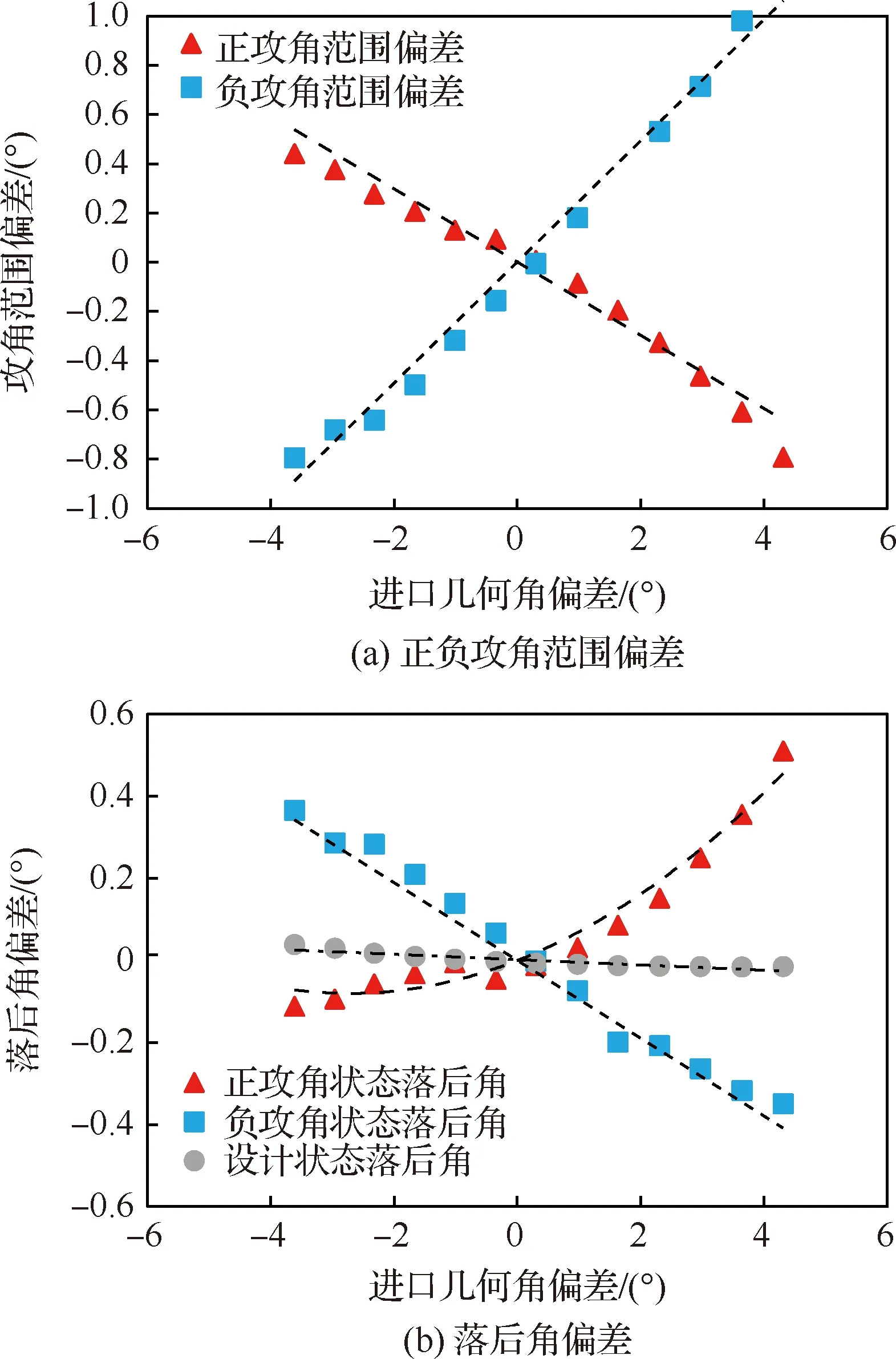
图30 进口几何角偏差对叶型性能影响的量化分析Fig.30 Quantitative analysis of effect of inlet geometric angle deviations on blade performance
4.2 叶身加工偏差的影响
与前面对于前缘偏差的分析类似,对叶身加工偏差影响的分析则保留了30%弦长之后的实际偏差,而设定前缘偏差为0,同样在10%~30%弦长范围内平缓过渡。图31给出了不同叶型的加工偏差分布对比示意图。
图32给出了保留叶身加工偏差叶型的计算结果。叶身加工偏差对叶型正攻角状态损失的影响很小,对设计和负攻角状态的损失有一定影响,对所有状态的落后角影响都较大。

图31 实际加工偏差、叶身加工偏差和叶身 均匀偏差示意图Fig.31 Diagram of manufacture deviation, body manufacture deviation and body uniformity deviation

图32 叶身加工偏差对叶型气动特性的影响Fig.32 Effect of blade body manufacture deviations on blade aerodynamic performance
基于前面的分析可知,气动性能对叶身部分的几何偏差敏感性较低,考虑到叶身加工偏差的轮廓度变化率较小,接近均匀偏差,若叶身偏差敏感性近似线性变化,可将偏差轮廓度的平均值作为评估叶身实际偏差的模型。图31还给出了将叶型实际叶身加工偏差平均后与实际偏差对比的结果。将所有实际叶型的叶身偏差平均后叠加在基准叶型上进行计算,得到如图33所示的结果。与图32对比可知,叶身均匀偏差对叶型损失的影响基本上复现了叶身实际加工偏的影响,但对落后角特性不确定度的模拟偏小。由此可见,采用均匀偏差的形式模拟实际叶身加工偏差是基本可行的,并且叶身偏差主要影响最小损失和负攻角性能,这应该是叶片厚度变化带来通道内的通流能力和速度变化造成的结果,这种现象在高马赫状态应该会更为显著。但是均匀偏差预测叶型落后角特性的能力较低,这或许是由于均匀偏差不能体现叶型的出口几何角的变化,在后续的工作中需要根据尾缘偏差对其进行进一步的修正。
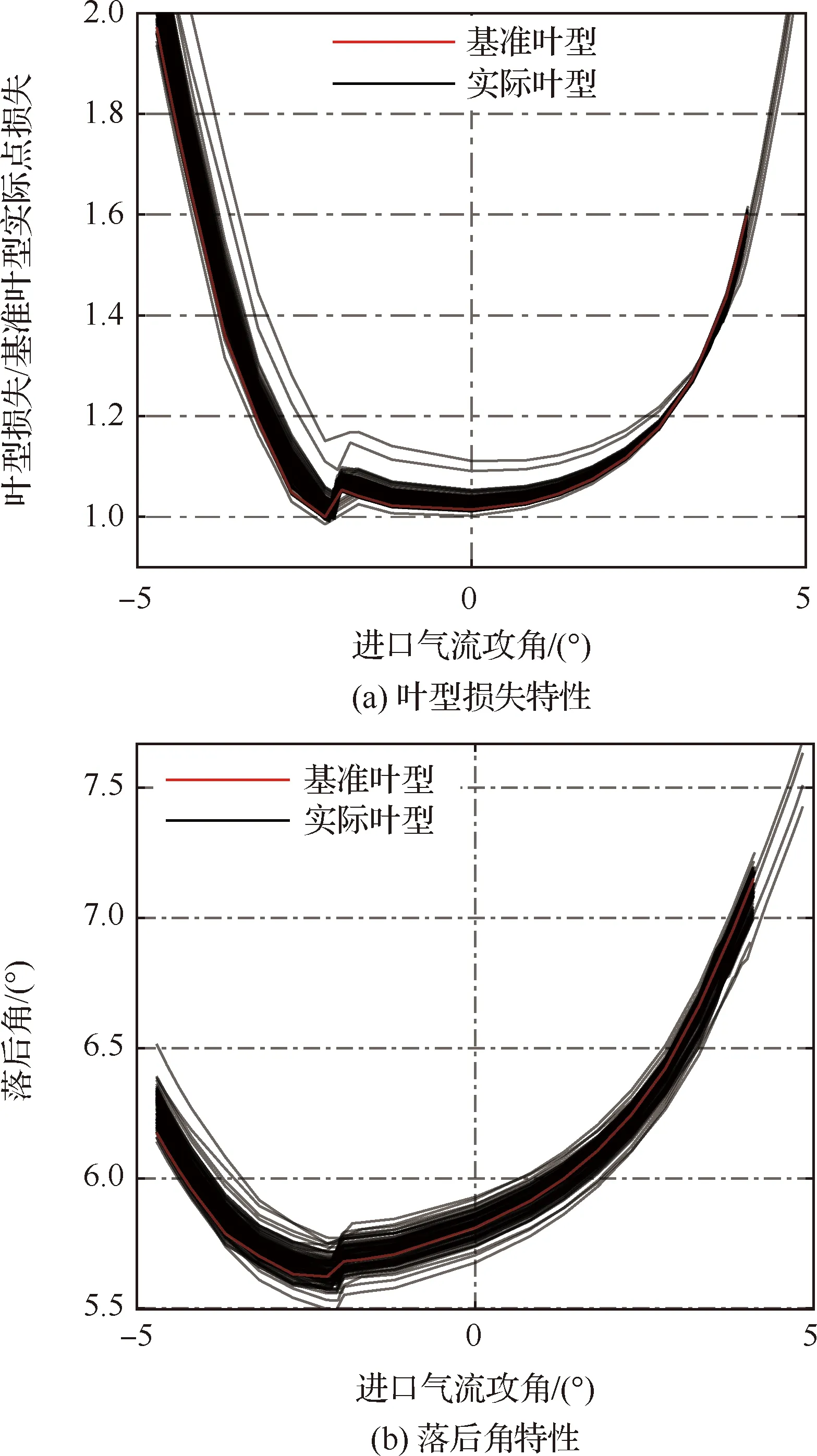
图33 叶身均匀偏差对叶型气动特性的影响Fig.33 Effect of blade body uniformity deviations on blade aerodynamic performance
5 结 论
以某高压压气机出口级叶片叶中截面的实际测量数据为基础,对叶片的实际加工偏差进行了测量和统计分析,计算了实际加工叶型的气动特性,并对不同区域加工偏差对叶型性能的影响机理做了深入分析,获得了以下结论:
1) 实际加工叶型的局部偏差特征表现为:前缘的轮廓度偏差略大于叶身,但偏差轮廓度变化率明显大于叶身,加工偏差对前缘形状的影响更明显;加工偏差在尾缘偏向于正偏差,轮廓度变化率较大,加工不确定度也最大;叶身的加工偏差要小于前尾缘,且偏差的轮廓度变化率较小,在很大范围内都类似均匀偏差;叶表不同特征点的局部加工偏差分布总体上符合正态分布,但是在前尾缘处如果存在系统性的进出口几何角偏差,会导致局部偏差的统计结果偏离正态分布。
2) 实际加工叶型的整体偏差特征表现为:叶型的进出口几何角偏差总体上表现为较强的正偏差,与前尾缘局部偏差存在明显的耦合;叶型的安装角偏差总体较小;总体几何偏差的分布特征都偏离正态分布,总体表现为进口几何角大偏差的出现几率偏高,而出口几何角小偏差的几率较大,安装角偏小的概率较大。
3) 实际加工叶型的气动特性存在较大的系统性偏差,这样的系统性偏差一方面来源于系统性的实际加工偏差,另一方面是由于加工偏差对叶型性能的影响有较强非线性效应,即实际叶型的损失或落后角的平均值与平均叶型的损失和落后角不相等,这种现象在正攻角状态表现更为明显。
4) 对流动机理的分析表明,在设计状态以及正负攻角状态下叶型的附面层对前缘附近约前10%弦长范围内的流动比较敏感。该区域内的加工偏差对附面层的发展影响较大,当流动存在局部分离现象时,附面层对加工偏差的敏感性会进一步提高。
5) 前缘的加工偏差是造成叶型性能变化的主要因素,其中进口几何角偏差对正负攻角状态下的叶型损失和落后角均有较大影响,且在正攻角状态下表现出了一定的非线性特征。
6) 可以用均匀偏差来近似估计叶身加工偏差对叶型正负攻角范围和损失的影响,如果需要进一步准确确定对落后角的影响,还需要考虑不确定度较大的尾缘偏差。
[21] 程超, 吴宝海, 郑海, 等. 叶片加工误差对压气机性能的影响[J]. 航空学报, 2020,41(2):623237.
CHENG C, WU B H, ZHENG H, et al. Effect of blade machining errors on compressor performance[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(2):623237 (in Chinese).

