基于3D Zernike矩的巡检器与空间站的相对导航算法
王润,郁丰,*,周士兵,刘方武
1. 南京航空航天大学 空间光电探测与感知工业和信息化部重点实验室,南京 211106 2. 南京航空航天大学 航天学院,南京 211106 3. 中国科学院 上海技术物理研究所,上海 200083
近些年来,随着空间任务的日益复杂,各个国家和研究机构针对空间在轨服务技术展开了大量的研究工作[1-2]。作为在轨服务领域中不可或缺的一部分,航天器表面自主在轨巡检技术对于一些大型航天器的长期安全运行、空间操作辅助等具有十分重要的价值[3]。
相对位姿测量是在轨巡检的前提,也是目前国内外科研人员的研究热点[4]。美国NASA约翰逊空间中心的工程师设计开发了一颗自主舱外机器人相机(Mini AERCam)[5]。旨在帮助宇航员及地面成员在任务执行期间观察航天器外部情况。但上述研究存在一定的局限性,Mini AERCam采用惯性/全球定位系统(Global Positioning System, GPS)导航,虽然GPS精度相对较高,但在GPS信号较弱或不存在的情况下,该导航方式会失效[6]。因此,开展新的面向自主在轨巡检的相对导航算法具有十分重要的意义。
目前,视觉测量系统和惯性推算系统广泛应用于航天器相对导航领域。由于TOF(Time of Flight)相机具有快速获取场景深度信息、不受光照环境限制等优点[7-8],因此近些年来多采用TOF相机对目标航天器表面点云进行采集,再利用图像处理算法解算航天器间的相对位姿参数[9]。例如,德国锡根大学、基尔大学和柏林大学的研究人员利用TOF相机快速、实时获取周围场景深度信息,而后采用ICP(Iterative Closest Point)算法完成位姿解算[10]。虽然ICP算法在航天领域应用广泛并进行了诸多改进,但其仍存在对初值的精度要求高、耗时长等弊端[11-12]。故而,目前多采用特征描述子对目标关键点进行描述,得到点对点的匹配后利用ICP算法对匹配结果进行优化,进而达到较好的导航效果。例如,Endres等提出了RGBD-SLAM(RGB Depth map-Simultaneous Localization and Mapping)算法[13],该算法采用SIFT(Scale-Invariant Feature Transform)/SURF(Speeded Up Robust Features)/ORB(Oriented FAST and Rotated BRIEF)进行特征提取和匹配,然后采用ICP算法改善位姿估计,能够稳定可靠地实现匹配定位。但现有的视觉SLAM采用的图像特征的语义级别低,造成了特征的可区别性较弱,可利用性有限[14],不适用于目标表面特征不明显的情况。SAC-IA(SAmple Consensus Initial Aligment)+ICP算法先采用FPFH(Fast Point Feature Histograms)描述子获取粗匹配结果,后利用ICP算法进行精确匹配[15-16],该算法精度较高且对表面特征不明显的目标具有较强的适用性,但其计算量较大,导致匹配耗时较长。Novotni和Klein和提出了一种用于描述三维曲面特征的3D Zernike描述子[17],使算法具有识别能力强、抗噪及抗旋转性能好等优势;该算法属于面匹配算法,直接利用三维地形曲面代替整个三维地形,保证了曲面上全部点均可参与匹配,使特征点能够很好地描述三维地形,获取高精度的匹配结果。3D Zernike矩匹配算法的耗时与其匹配阶次和目标表面结构有关,耗时上具有可控性[18-19],因而近些年来逐渐应用于导航系统中。但目前基于3D Zernike矩的导航研究仅实现了匹配定位功能,尚未能解算出目标的位姿参数。因此,研究如何利用3D Zernike矩算法解算航天器间的相对位姿参数是实现两航天器间相对导航的关键,具有一定的现实意义。但由于TOF相机无法直接获得速度和角速度信息,且受测量距离、外界环境情况等影响较大,因此,仅利用图像处理技术进行航天器间的相对导航有时无法达到预期的效果。相比之下,惯性位姿推算系统则可连续输出载体的加速度、角速度信息且不依赖于外界环境,具有短期高精度和高稳定性等优点,但由于惯性元件存在初始误差、漂移和噪声等因素,长时间导航会产生较大的积累误差[20]。
鉴于视觉测量系统和惯性位姿推算系统均存在其各自的优缺点,本文设计了“视觉/惯性”组合导航系统,以空间站表面为“特殊地形”,利用TOF相机获取空间站表面“三维地形曲面”。采用一种基于3D Zernike矩的面匹配算法,以空间站表面三维地形曲面代替空间站表面三维地形,通过地形曲面的匹配实现三维地形的匹配[21-22],求解出匹配前后两曲面间的相对位姿参数,将该位姿参数与惯性系统推算的相对位姿参数进行信息融合,从而实现航天器间的相对导航,以期有效、高精度地估计空间站与巡检飞行器间的相对位姿信息,满足相关应用领域的需求。
1 系统总体设计
以空间站表面巡检为背景,研究“视觉/惯性”组合系统的航天器相对导航算法,系统总体结构如图1所示。
首先通过TOF深度相机获取空间站表面局部三维点云数据,以该数据为实时图,以导航计算机中空间站外表面先验点云数据为基准图,然后在3D Zernike矩框架下实现实时图与基准图的匹配,并解算实时图与匹配上的基准图间的相对位姿,最后将该相对位姿与惯性系统推算的相对位姿通过扩展卡尔曼滤波器(EKF)进行信息融合,从而实现两航天器间的相对导航。
2 3D Zernike矩配准算法
2.1 3D Zernike矩的定义及性质
(1)

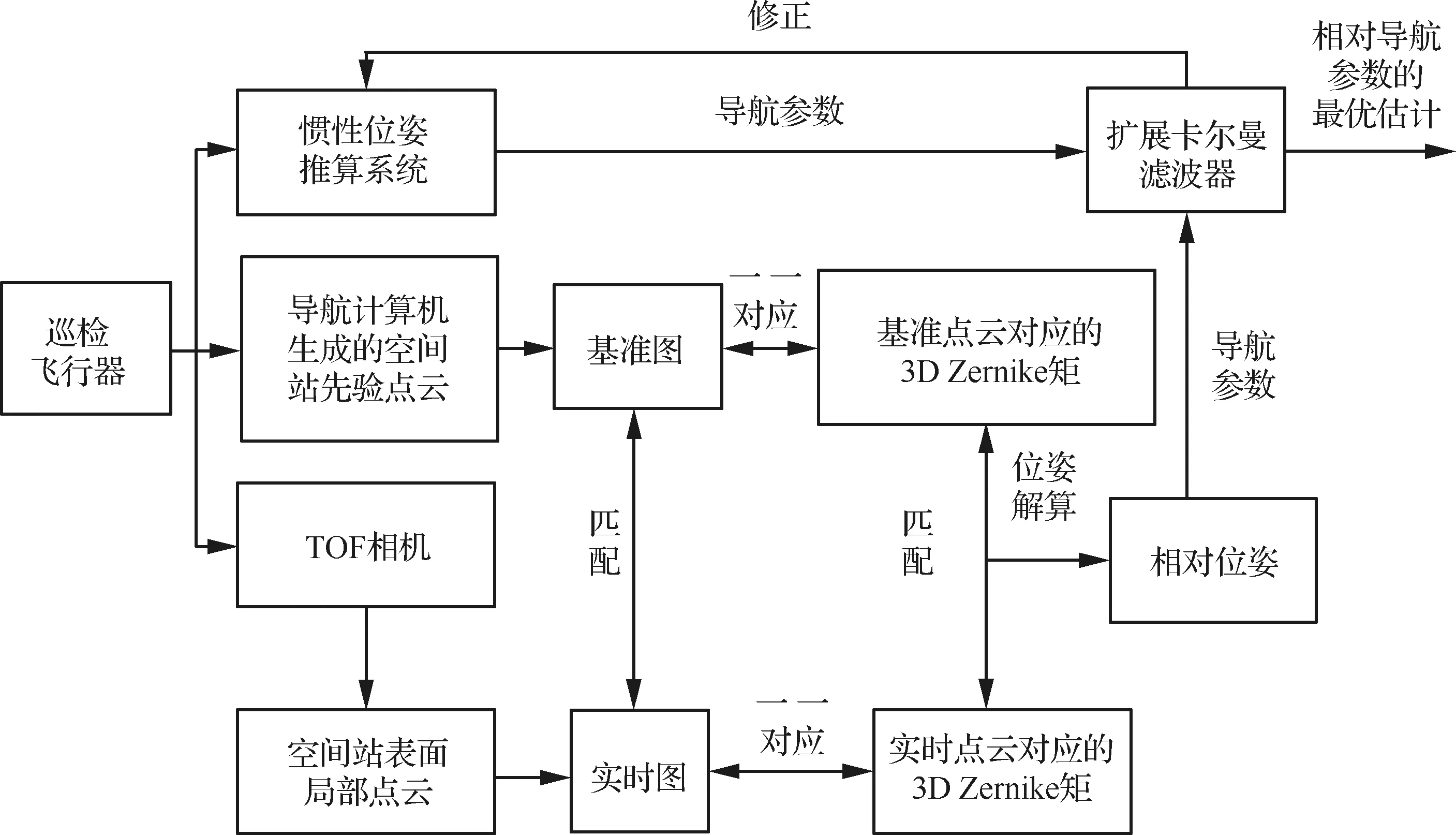
图1 系统结构Fig.1 System structure

(2)

(3)
(4)
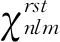
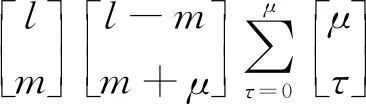
(5)
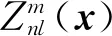
(6)

(7)
式中:Mrst为几何矩,定义为
(8)
当x为三维曲面上的点时,f(x)=1;当位于其他位置时,f(x)=0。故而Mrst的离散形式为
(9)
式中:N为点云中所有点的个数。
(10)
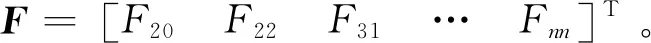
2.2 基于点云的3D Zernike矩匹配算法
由2.1节中3D Zernike矩的定义及性质可知,3D Zernike矩与空间站三维曲面存在一一对应关系,且在匹配过程中,整个三维地形曲面上的点均可参与匹配,这保证了曲面特征的完备性,能够较好地描述地形特征[25-26]。因而提出了一种基于3D Zernike矩的航天器相对导航算法。利用3D Zernike矩表示空间站三维外表面模型,从而将曲面匹配转化为3D Zernike矩的匹配问题。具体算法步骤如下:
1) 将导航计算机中空间站外表面三维点云作为3D Zernike矩匹配的基准图。
2) 根据描述三维曲面的精度要求和计算时间要求,预先设置匹配所需要的3D Zernike矩的计算阶次n。
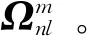
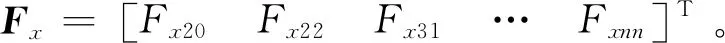
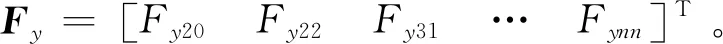
6) 由于3D Zernike矩描述子向量各元素间的数量级不尽相同,故而以Canberra距离作为特征向量间的距离测度来消除该问题所产生的判别误差。Canberra距离d越小,实时图与当前窗口对应的基准图越相似,Canberra距离定义为
(11)
式中:Fxi和Fyi分别为Fx和Fy的组成元素,且Fxi≥0,Fyi≥0,Fxi+Fyi≠0。
7) 当窗口在基准图上遍历一次后,得到一组Fxi与Fyi之间的Canberra距离di。将di从小到大排序,di最小的窗口位置即为实时图与基准图相似度最大的位置,从而完成实时图在基准图上的匹配。
2.3 相对导航参数的求解
在完成3D Zernike矩匹配后,进一步求解实时图与相似度最大的基准图窗口间的相对位置、相对姿态,从而确定巡检器飞行器与空间站间的相对导航参数。具体算法步骤如下:

3) 点集pi和点集qi的中心点分别为μp和μq:
(12)
4) 点集pi和点集qi中心化处理后,其协方差矩阵为
(13)
5) 由矩阵K中各元素kij(i,j= 1, 2, 3, 4)构造出四维对称矩阵G:

(14)
6) 对G进行特征值分解,求得最大的特征值以及其对应的特征向量:
(15)


(16)
T=μq-Rμp
(17)
8) 利用第7)步求得的旋转矩阵R和平移矩阵T对pi进行旋转和平移变换,得到新的对应点集p′i=Rpi+T。

3 相对位姿参数滤波器的设计
3.1 状态方程的建立
利用惯性测量单元测量巡检器的加速度和角速度信息,测量值分别为fc和ωc,由于惯性测量单元中加速度计和陀螺仪的随机测量误差一般含有多种成分的有色随机噪声,建立其数学模型必须进行“白色化”处理,假设:
fc=f0+fb+fε
(18)
ωc=ω0+ωb+ωε
(19)
式中:f0为加速度真值;fb为加速度计漂移;fε为加速度计测量噪声;ω0为角速度真值;ωb为陀螺漂移;ωε为陀螺测量噪声。
由于主要研究航天器表面巡检,巡检器与空间站间的相对距离较小,Hill方程具有足够的精确性。根据Hill方程,在空间站轨道坐标系下建立两航天器质心间的相对位置运动学模型:
(20)

假设空间站轨道坐标系为导航坐标系,推导巡检过程中两航天器间的相对姿态运动学模型为
(21)
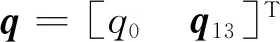
由式(19)、式(21)可推导出巡检器相对于空间站的姿态运动方程:
(22)

(23)
式中:fbε和ωbε分别为加速度计和陀螺的漂移噪声。
对式(20)、式(22)和式(23)中非线性部分线性化处理推导出系统的线性化状态方程:
(24)
3.2 观测方程的建立
以TOF相机获取的空间站表面局部点云数据为实时图,以空间站表面先验点云数据为基准图。由于深度相机采集的点云数据往往带有噪声,为避免其对匹配性能的影响,需先对实时图与基准图的原始点云数据进行滤波降噪处理,后利用3D Zernike矩匹配算法进行相对位姿的测量,以获得较好的相对位姿参数。惯性位姿推算系统提供测量时的相对位置ρ和相对姿态q。则观测方程为
(25)
式中:ρc和qc分别为巡检器相对于导航坐标系的位置和姿态观测值;ρε和qε分别为实时图与基准图间的相对位置和姿态误差。
同样对观测方程进行线性化:
(26)
式中:δqc13和qε13分别为δqc和qε的矢量部分。
4 实验及结果分析
4.1 3D Zernike矩匹配算法的验证
为验证所设计算法的有效性,进行了实验平台的搭建。假设空间中空间站的长度为10 m,巡检器与空间站间的距离为6 m。巡检器位于空间站下方6 m处,而后沿空间站轨道系X轴正方向运动。根据TOF相机的视场范围,空间中实时图的大小约为(3×4) m。将上述场景等比例缩小10倍,在搭建的实验场景中模拟航天器在空间中的运动如图2所示,空间站模型长度约为1.0 m, 巡检器与空间站模型间的距离约为0.6 m, 运动过程中TOF相机拍摄的模型实时图大小约为(0.3×0.4) m。由于巡检器以及空间站的三轴姿态可能均存在小角度的偏差,这种偏差会导致实时图与基准图边缘点云数据的差异,为避免边缘差异点对匹配结果的影响,以实时图的重心为中心,在实时图内部截取(0.2×0.2) m的矩形作为匹配模板,并将实时图依次与基准图进行配准,得到实时的相对位置、姿态参数作为后续信息融合的观测量。

图2 实验平台Fig.2 Experimental platform
3D Zernike矩的计算耗时与其匹配阶次成指数关系,而匹配阶次的选取与地形起伏情况有关,地形起伏越剧烈,所需匹配阶次越高。根据采用的空间站模型外表面起伏变化情况、配准精度及时间要求,预先设置匹配阶次n=4。假设巡检飞行器运行过程中某一时刻实时图如图3所示,此时实时图与基准图间的相对位姿分别为[0.1, 0, 0] m、[1, 1, 1]°。将该实时图与基准图在3D Zernike矩框架下进行匹配及相对位姿解算,结果如图4所示。

图3 实时图Fig.3 Real-time map
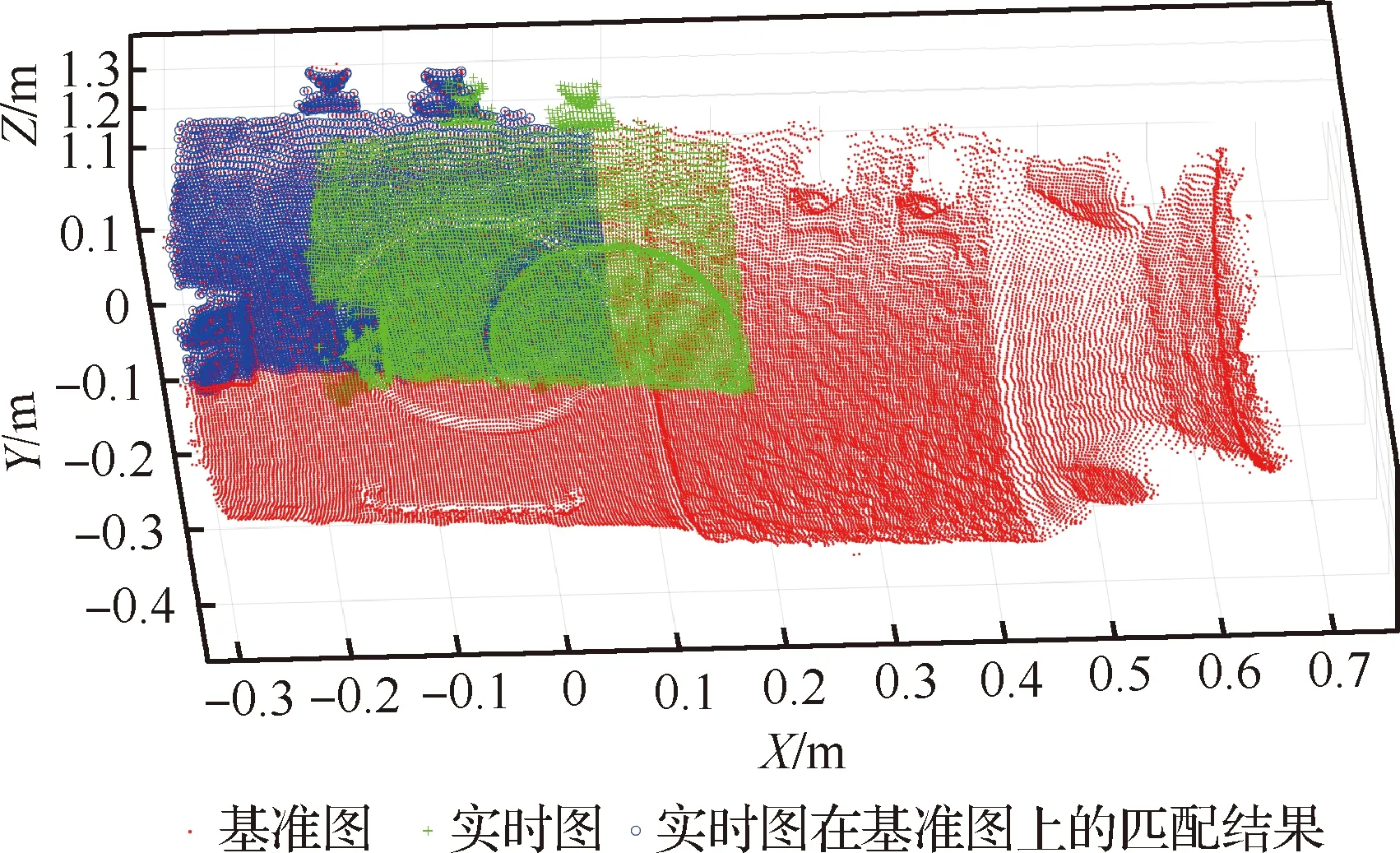
图4 匹配结果Fig.4 Matching results
由图4的实验结果可知,基于3D Zernike矩的匹配算法能够实现实时图在基准图上的匹配,相对位置精度优于0.005 m,相对姿态精度优于0.3°。但在实际情况中,实时图与基准图间的位姿差异及点云数量的不同会导致配准效果的不同,从而对导航系统的精度产生一定的影响。故而进一步研究了3D Zernike矩匹配精度及速度的主要影响因素。
4.1.1 姿态差异对配准精度的影响
假设实时图与基准图间三轴位置差异值为[0.1, 0, 0] m;将上述实时图与基准图间的三轴角度差异值依次设置为[1, 1, 1]°、[2, 2, 2]°、[3, 3, 3]°、[4, 4, 4]°,则采用3D Zernike矩匹配后解算出的相对位姿误差如图5所示。

图5 相对位姿误差Fig.5 Relative pose errors
由图5可知,实时图与基准图间的姿态差异越大,3D Zernike矩匹配误差越大,解算出的相对位姿参数误差越大。此外,由于三轴角度变化过程中俯仰角的变化会导致实时图点云在俯仰轴上的大幅度移动,故而Y轴的相对位姿误差最大,而航向轴作为平面内轴向,受三轴角度变化的影响最小,因而Z轴的相对位姿误差最小。
4.1.2 点云数量对配准耗时的影响
在保证相同位姿参数条件下,采用点数分别为8 000、9 000、10 000、11 000的实时图依次与基准图进行匹配,3D Zernike矩匹配的计算耗时如图6所示。
由图6可知,预先匹配阶次及基准图一定的前提下,参与匹配的实时图点云数量与3D Zernike矩匹配的计算耗时成正比关系,点云数量越多,计算耗时越长。
4.1.1节和4.1.2节的两组实验证明,姿态差异越大、点云数量越多,3D Zernike矩匹配算法测量的观测值误差及延迟越大,故而在后续信息融合过程中需充分考虑上述影响因素,以达到较好的导航精度。
4.2 组合导航算法验证及分析
根据第3节中建立的系统模型,分别设置滤波器的各项参数,滤波初值的协方差矩阵为
(27)
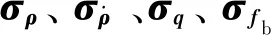


表1 滤波参数Table 1 Filtering parameters
在表1和表2的仿真条件下进行校验,得到相对位置和姿态估计误差如图7和图8所示。

表2 初始仿真误差参数Table 2 Initial simulation error parameters
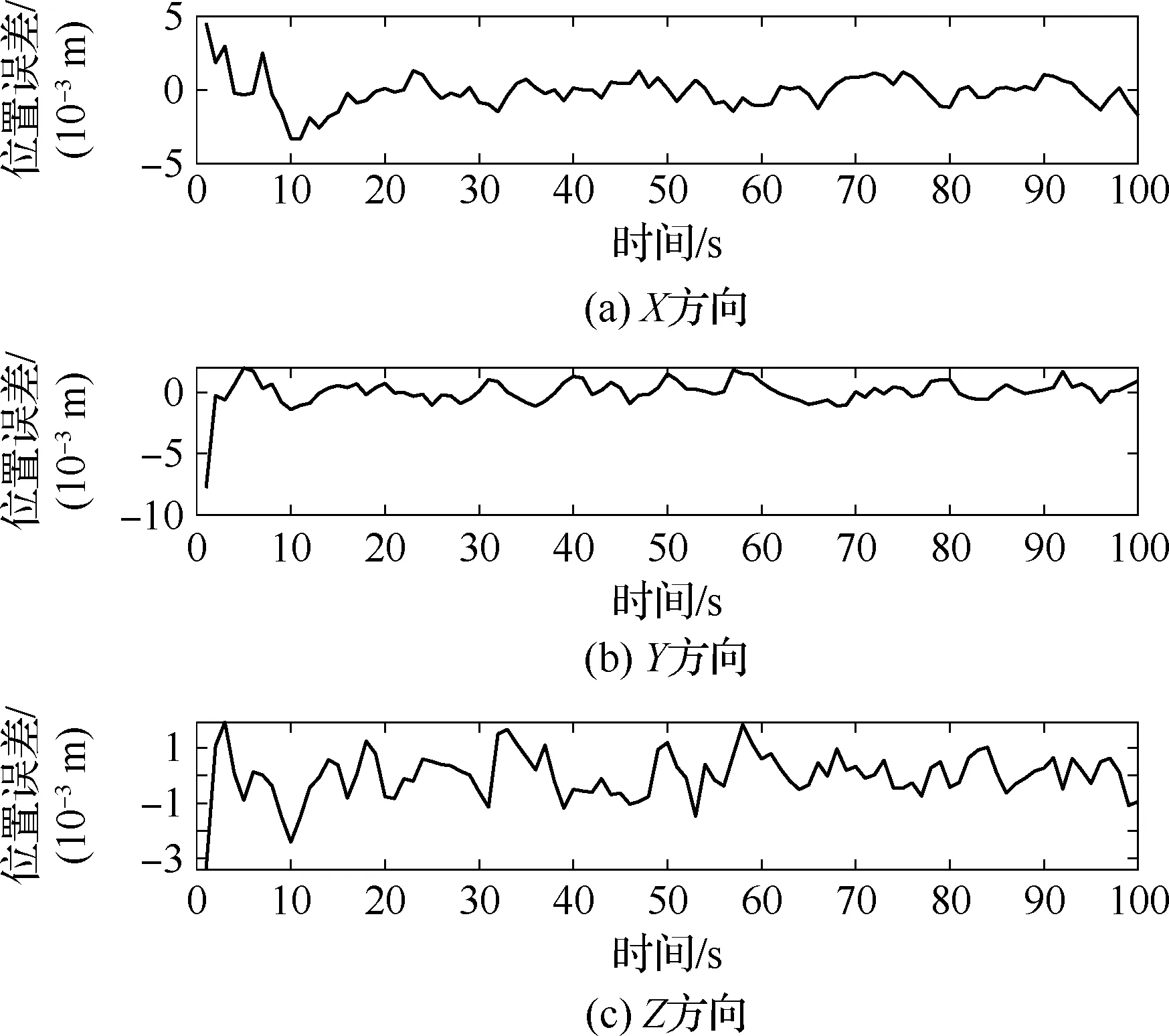
图7 相对位置估计误差Fig.7 Relative position estimation errors
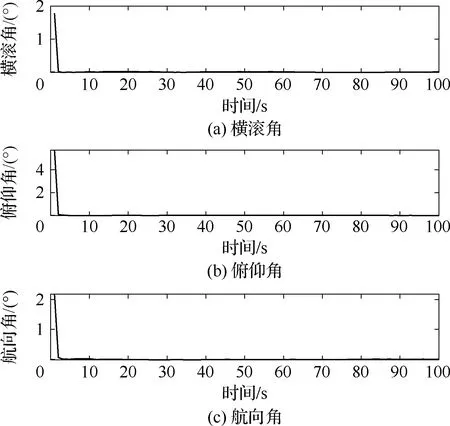
图8 相对姿态估计误差Fig.8 Relative attitude estimation errors
仿真结果表明,设计的信息融合方法能有效获取巡检器与空间站间的相对导航参数。相对位置和姿态在很短的时间内收敛,滤波效果较好。
为进一步证明设计的“3D Zernike矩+惯性”组合导航算法的有效性,将该组合导航算法与上述3D Zernike矩算法以及相同实验条件下导航效果相对较好的“SAC-IA+ICP”算法进行实验对比。3种算法的配准误差及耗时结果如表3所示。

表3 配准误差及耗时Table 3 Registration errors and time-consumption
由表3实验结果可知,3D Zernike矩配准算法在精度及耗时方面优于“SAC-IA+ICP”算法;此外,设计的组合导航算法精度优于3D Zernike矩算法,能够估计出巡检飞行器与空间站间的最优相对位姿参数,实现高精度相对导航。
此外,还对加速度计、陀螺仪的漂移误差进行了估计。在表1和表2的仿真条件下,加速度计和陀螺仪的漂移估计误差如图9和图10所示。
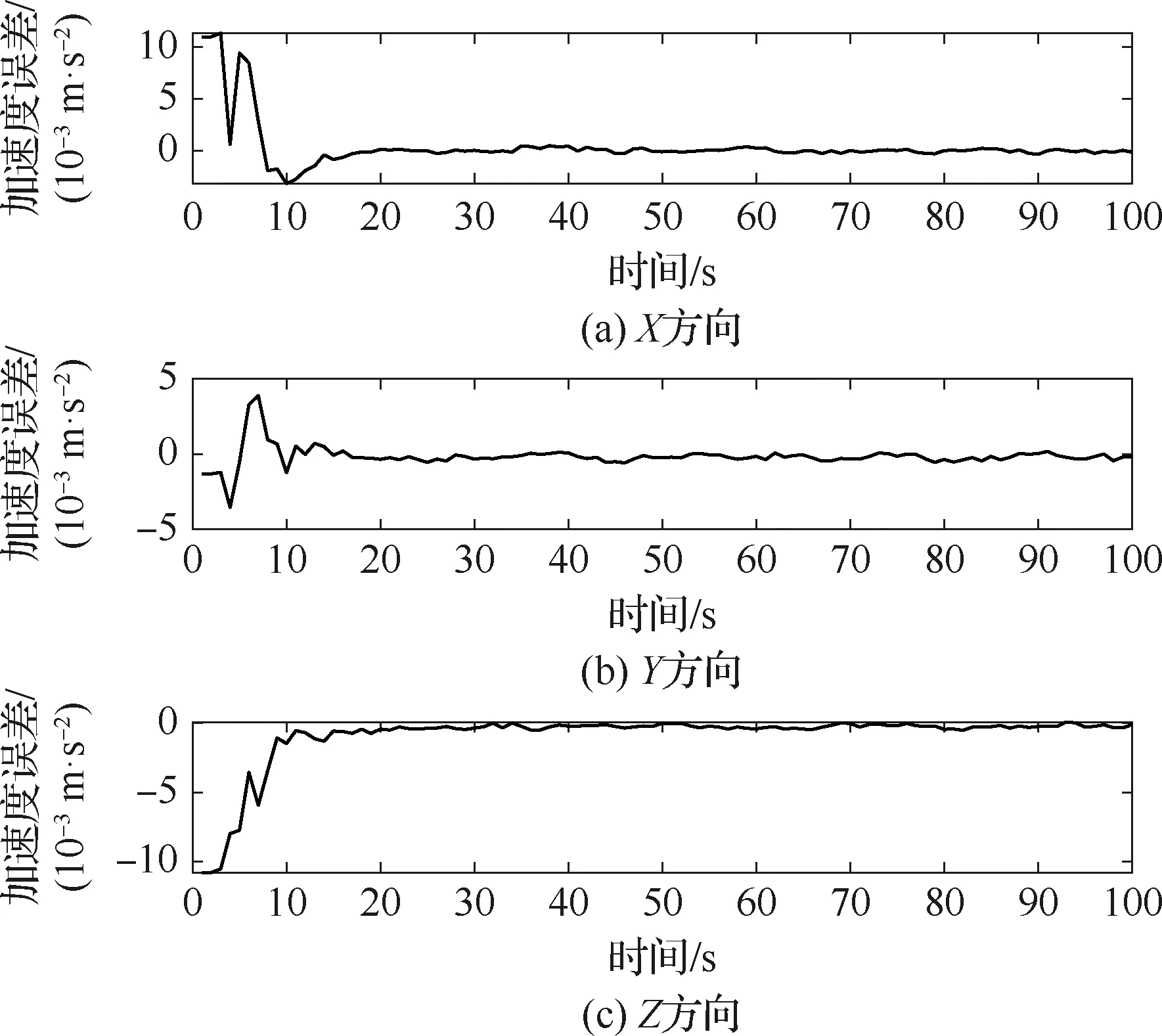
图9 加速度计漂移估计误差Fig.9 Accelerometer drift estimation errors

图10 陀螺仪漂移估计误差Fig.10 Gyroscope drift estimation errors
由图9和图10可知,惯性测量单元加速度计和陀螺仪漂移误差能够很快收敛,收敛后几乎无波动;加速度计漂移估计精度优于0.005 m/s2,陀螺仪漂移估计精度优于16.5 (°)/h;表明了本文算法的有效性,可以在一定程度上补偿加速度计和陀螺的漂移。
5 结 论
以空间站表面为“特殊地形”,提出了一种大型航天器表面巡检的相对导航算法。创新地采用3D Zernike矩匹配算法实现了TOF相机采集的局部实时图在先验基准图上的定位,并解算实时图与基准图间的相对位姿参数,同时进一步分析了影响3D Zernike矩匹配算法精度及耗时的主要因素。以该相对位姿参数为观测量设计扩展卡尔曼滤波器对惯性位姿推算系统的误差进行校正,从而估计出巡检飞行器与空间站间的最优相对导航参数,为大型航天器近距离在轨巡检操作的安全可靠性提供了技术支持。
[21] WANG K D, ZHU T Q, WANG J L. Real-time terrain matching based on 3D zernike moments[J]. The Journal of Navigation, 2018, 71(6): 1441-1459.

