尾座式无人飞行器鲁棒容错编队控制

刘德元，刘昊,*，Frank L LEWIS

1. 北京航空航天大学 宇航学院，北京 100083 2. 德克萨斯大学阿灵顿分校 德克萨斯大学阿灵顿研究所，沃斯堡 76118

近几年来，尾座式无人飞行器受到了广泛关注[1-3]。该飞行器具有旋翼飞行器的垂直起降能力和固定翼飞行器的续航能力，因此，可以像固定翼飞行器那样高速飞行，也可以像旋翼飞行器那样垂直飞行，可以执行3种飞行模式：垂直飞行、过渡模式飞行和水平飞行。因此，与传统的固定翼和旋翼飞行器相比，尾座式无人机可以执行相对复杂的任务。

与单架飞行器相比，多架飞行器协同执行任务可以提高工作效率。因此，多无人机编队技术可被广泛应用于森林火灾的协同探测、环境的协同监测、电力线路的分布式检测等多个领域[4-5]。但是，在实际的编队飞行中，执行器往往会频繁出现故障，严重影响编队系统的性能，甚至引发灾难性事故。因此，为提高无人机编队的安全性和容错能力，研究多无人机编队的容错编队控制方案具有重要意义。

对于多架尾座式飞行器来说，不同的飞行模式可以形成不同的编队构型，并且编队构型可以随着飞行模式的改变而切换。例如，在垂直起飞阶段，编队构形可以依据场地条件而改变，在水平飞行时，可以像鸟类一样变换编队构型。然而，为多架尾座式无人飞行器设计容错编队控制协议具有很大的挑战性，特别是在飞行模式转换过程中。首先，多架飞行器可能同时发生多个执行器故障，这可能导致设计的控制器是不可行的。而且，飞行模式转换是一个包含垂直和水平飞行模态的大机动飞行过程，姿态角会发生剧烈变化，这可能导致飞行器模型中存在严重的非线性和强耦合动态，精确的飞行器编队动态模型很难获得。此外，飞行器编队会不可避免地受到外界环境干扰的影响。

现有的研究主要集中在单架尾座式飞行器的飞行控制上。为实现无人机的飞行模式切换，刘志豪等[1]设计了PID控制器。Lyu等[2]提出了一种尾坐式垂直起降无人机在外界干扰下的控制方法。Banazadeh和Taymourtash[6]提出了一类实现尾座式飞行器轨迹跟踪的最优控制策略。Zhong等[7]设计了一种实现双旋翼尾座式飞行器悬停飞行的自适应控制方法。然而，对于多架尾座式无人飞行器的编队控制问题还没有得到充分的研究。

一些研究集中于常规无人机的编队控制。Dong等[8]针对多架四旋翼编队飞行，设计了一种编队跟踪控制协议。张民等[9]提出了一种基于Leader-Follower编队的无人机协同跟踪控制方法。徐博和张大龙[10]针对多架固定翼，设计了一种最优编队控制策略。张佳龙等[11]基于反步推演法，提出了一种无人机编队队形协同导引控制方法。但是，在这些文献中，没有考虑执行器故障的影响。Xu等[12]为了实现编队稳定飞行，提出了一种多无人机容错控制策略。张普等[13]针对领航者系统出现故障引起编队通讯中断而不能完成任务的问题，提出了一种基于一致性理论的分布式自适应控制方法。马广富等[14]针对航天器编队飞行过程中的故障问题，提出了一种自适应轨道控制方法。Yang等[15]针对多架三自由度直升机在执行器故障情况下的姿态协同问题，设计了一种姿态协同控制器。但是，在这些文献中，没有讨论外部干扰和多种不确定性的影响。因此，在多个执行器故障和不确定性情况下，多架尾座式无人飞行器的编队控制问题需要进一步研究。

本文针对尾座式无人飞行器编队在执行器故障和多种不确定性影响下的控制问题，提出一种鲁棒容错编队控制方法，实现期望的编队飞行。对于每架飞行器，所设计的控制器由一个标称控制器和一个干扰补偿控制器组成。设计标称控制器实现期望的系统控制性能，利用干扰补偿控制器抑制执行器故障和多种不确定性的影响。本文的创新点主要有以下3点：① 多架尾座式无人飞行器可以执行连续的模式转换编队飞行；② 在编队飞行过程中，同时考虑多个执行器故障。这些故障对全局闭环控制系统的影响可以被所设计的控制器抑制；③ 设计的编队协议可以抑制参数不确定性、非线性和耦合以及环境干扰的影响，保证编队飞行的鲁棒性。

1 问题描述

1.1 图 论

考虑N个尾座式无人飞行器，它们之间的信息交换可以由一个有向图G=(V,E,W)表示。V={vi,i∈N}表示节点集合，E⊆V×V表示边集合，W=[wij]∈N×N表示权重矩阵。如果飞行器i和飞行器j之间存在一个边，例如(vi,vj)∈E，则表示飞行器i可以收到飞行器j的状态信息。若(vi,vj)∈E则wij>0，否则wij=0。定义Ni={j|(vi,vj)∈E}为节点vi的邻居集合，D=diag(di)∈N×N为有向图G的度矩阵，其中系统通信拓扑图G的拉普拉斯矩阵可以表示为L=D-W。如果存在一个具有指向所有其他节点的有向路径节点，则系统通信拓扑图G具有一个生成树，并且该节点称为树的根。

1.2 尾座飞行器模型

图1为一种尾座式无人飞行器编队飞行的3种飞行模式。该尾座无人飞行器由1个机身、4个旋翼、1对共轴螺旋桨、2个副翼和2个机翼组成[3]。4个旋翼和共轴螺旋桨提供飞行中的主要推力或升力,机翼和副翼提供水平飞行时的升力。

第i个尾座飞行器的动态模型为[3]

(1)

图1 尾座飞行器编队飞行模式Fig.1 Formation flying mode of tail-sitters

(2)

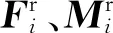
(3)

(4)

(5)

(6)

式中：

常见的执行器故障主要分为完全失效故障和部分失效故障。完全失效等同于该执行器不能为所在轴提供任何力和力矩。部分失效等同于只能产生部分控制力和力矩。在本文中，引入执行器效率损失因子来表示故障等效的损失力和力矩。因此，执行器模型可以表示为

(7)

式中：Mi,c0=Λi1Ui1+Λi2Ui2，Fi,c0=Λi3Ui1为没有故障时的控制力和力矩；Γi,r1=diag(σi,r1,σi,r2,σi,r3,σi,r4),Γi,a1=diag(σi,a1,σi,a2,0,0),σi,rj,σi,ak∈[0,1],j=1,2,3,4,k=1,2,σi,rj和σi,ak为执行器效率损失因子。σi,rj=σi,ak=1表示执行器完全失效，σi,rj,σi,ak∈(0,1)表示执行器部分失效。

1.3 控制目标

本文目的是针对尾座式无人飞行器编队设计一种鲁棒容错编队控制方法，使其能够在执行器故障和多种不确定性条件下完成期望的编队飞行。

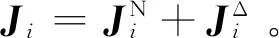
(8)

式中：Δip和Δia为等效扰动，具体表达式为

(9)

2 鲁棒容错编队控制器设计

(10)

(11)

在实际编队飞行中，得不到等效扰动Δip和Δia的具体数值，于是引入具有如下结构形式的鲁棒滤波器：

(12)

根据式(8)，可以得到

(13)

结合式(12)和式(13)，可以得到干扰补偿控制器的实现如下：

(14)

式中：ηip和ηia为滤波器状态；fip=diag(fi,p,fi,p,fi,p)，fia=diag(fi,a,fi,a,fi,a)。

3 鲁棒性分析

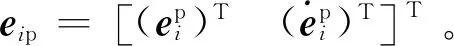
(15)

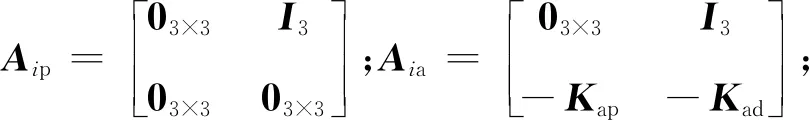
根据式(15)，可以得到以下全局闭环误差系统

(16)

式中：ep=[eip]∈6N×1和ea=[eia]∈6 N×1为全局闭环系统跟踪误差；Ap=IN⊗Aip-λg(L+BL)⊗Bk1Kt，Aa=IN⊗Aia,Bk2=IN⊗Bk1，且

定义Δp=[Δip]∈3N×1和Δa=[Δia]∈3N×1。根据式(16)，可以得到

(17)

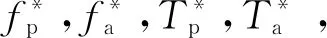
证明：结合式(9)和式(11)，可以得到

(18)

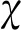
(19)

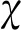
(20)

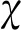
(21)

结合式(21)和式(17)，可以得到

(22)

若式(23)成立

(23)

结合式(17)和式(21)，可以得到

(24)

结合式(17)、式(22)和式(24)，可以得到

(25)

4 仿真结果

这一部分对所设计的尾座式无人飞行器编队容错控制方法在执行器故障和多种不确定性条件下进行仿真验证。在仿真中，考虑6架飞行器同时以六边形构型执行垂直起飞、模式转换、水平飞行任务。这6架飞行器初始条件设定为

飞行器2、4、5被选为故障飞行器，且在飞行时间为12 s时同时发生故障。对于飞行器2，故障模式为第4个电机完全卡死；飞行器4，所有执行器效率损失20%；飞行器5，第4个单机完全故障，其余执行器效率损失30%。

在仿真中，通信拓扑图G设置为：V={v1,v2,v3,v4,v5,v6}，E={(v6,v5),(v5,v4),(v4,v3),(v3,v2),(v2,v1)}，W=[wij]。飞行器1被选为通信拓扑图G的根。期望的虚拟领导者轨迹设为

在鲁棒容错编队控制的数值仿真中，选取标称控制器参数矩阵为：Kap=diag(130.4,120.6,130.6),Kad=diag(115.8,120.8,105.8),Kpp=diag(2.6,3.6,2.6),Kpd=diag(1.2,1.5,0.2)，鲁棒补偿器参数为：fi,p=1 500，fi,a=40。飞行器标称参数的选取来源于文献[3]，在仿真中选取的实际模型参数分别比标称值大25%。飞行器i受到的外界扰动为

所得到的结果如图2～图4所示，图2为飞行器编队的三维飞行轨迹，图3为编队的四元数姿态响应，图4为位置跟踪误差。为了验证所提出方法的优越性，应用文献[12]中设计的一个标称控制器作为对比。相应的位置跟踪误差如图5所示。从图2可以看出，对于所设计的编队控制器，飞行器编队在故障发生后仍可以很好地完成编队飞行任务。从图4可以看出，在多种不确定性和执行器故障条件下，所提出控制器的编队轨迹跟踪误差会稳定在一个较小的邻域内。从图5可以看出，对比控制器的轨迹跟踪误差，在故障发生后，呈发散状态，因此无法实现编队飞行任务。从以上结果可以看出，所提出的鲁棒容错编队控制方法可以使尾座式无人飞行器编队在执行器故障、参数不确定性、强非线性和耦合、外界扰动的影响下，仍能很好地完成编队飞行任务。

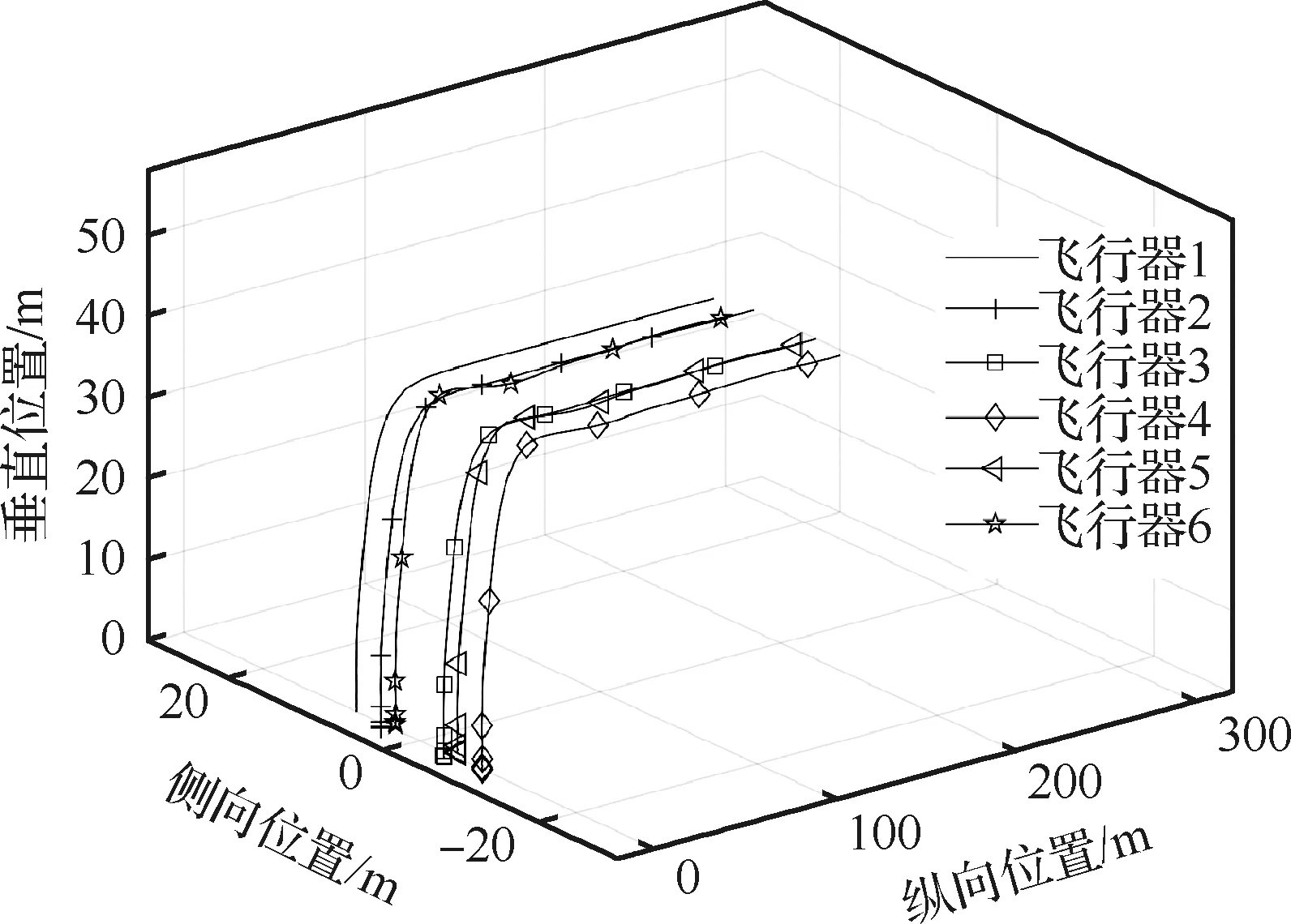
图2 所提控制器的编队飞行轨迹Fig.2 Formation flight path using the proposed controller

图3 所提控制器的编队四元数姿态响应Fig.3 Quaternion attitude response using the proposed controller

图4 所提控制器的编队轨迹跟踪误差Fig.4 Formation trajectory tracking errors using the proposed controller

图5 对比控制器的轨迹跟踪误差Fig.5 Trajectory tracking errors using comparison controller

5 结 论

本文针对尾座式无人飞行器在同时发生多个执行器故障和多种不确定性条件下，提出一种鲁棒容错编队控制方法。通过理论分析证明了在执行器故障、严重的非线性和耦合性、参数不确定性、外界扰动等影响下的全局闭环稳定性。最后通过数值仿真验证了算法的有效性。