多航天器分布式事件触发分组姿态协同控制
王帅磊,周绍磊,代飞扬,刘伟,闫实
(海军航空大学,烟台264001)
姿态协同控制是多航天器系统中的重要技术之一,广泛应用在如航天器编队飞行等领域[1-4]。近年来,研究人员对这一重要问题展开了深入的研究。当系统内所有航天器的姿态和角速度均达到一致时,称多航天器系统达到了姿态协同。
现有研究从多个方面对多航天器姿态协同控制问题进行了分析。对于领导-跟随结构的多航天器系统,Cai和Huang提出了一种分布式的观测器对领导者的状态进行估计,并且对角速度进行了补偿[5],考虑到系统中存在未知参数,进一步构造了分布式的自适应算法以使误差系统稳定[6];此外,针对外部扰动提出了自适应的处理方法[7]。文献[8]在SO(3)模型的基础上,设计了一种时变增益扩张状态观测器,并根据航天器之间的相对姿态构造了基于旋转矩阵的控制输入。对于联合连通拓扑上的多航天器系统,Liu和Huang证明了存在一种分布式观测器对目标进行估计[9],Lu和Liu也进行了类似的研究[10],并且在文献[9-10]中,系统拓扑都是有向的。Ma等对联合连通拓扑上的领导-跟随系统,设计了滑模变量和分布式的观测器对跟随者进行估计[11]。对于无领导者的多航天器系统,Huang等同时考虑了执行器故障及饱和约束,并设计了一种补偿方法[12]。文献[13]对带有机械臂的空间机器人,设计了一种卫星基座、姿态与机械臂一体化的控制器。文献[14]对电磁航天器编队悬停问题,构造了包含多个影响因素的不确定系统,对轨道姿态进行解耦,能够实现高精度悬停。
为了节约系统的通信和计算资源,降低航天器间收发信息的频率,事件触发机制被引入到了航天器姿态协同控制方法中[4,15-17]。在事件触发机制下,需要设计相应的事件触发函数,并且系统内的通信交互仅在事件触发函数被满足时才会执行,于是连续的系统通信被转化为不连续的间断通信,从而显著节约了系统的能源和资源。在文献[4]中,提出了一种分布式的事件触发控制器以处理执行器的故障,并同时考虑了外部扰动。Weng和Yue在领导-跟随结构下,提出了一种分布式的触发机制,能够通过领导者的状态构造一个凸包,并使所有跟随者的状态收敛到该凸包中[15]。Zhang等在无向拓扑上提出了一种依赖当前状态的控制律,其特别之处在于:触发函数下一次被满足的时刻可以根据航天器的当前状态进行预测[16]。Xu等构造了一种自适应的滑模控制方法,能够引导航天器跟随预先设计的姿态轨迹,并同时考虑了惯性不确定性及外部扰动[17]。针对SAR卫星,Fu等提出了2种带有时滞的基于终端滑模的控制律[18]。
大多数现有研究都致力于使多航天器的姿态收敛到某一个确定的时不变或时变的姿态。而随着技术的发展,以及多航天器越来越广泛的应用,在复杂的应用场景中,对航天器的姿态可能有不同的需求,即要求一部分航天器保持同一姿态,另一部分航天器保持另一姿态。例如,在卫星编队监控目标时,由于它们分布在空间中的不同位置,那么可以划分为若干个不同的分组,每个分组内部的卫星能够调整自身姿态以实现更好的观测。这种包含多个分组并使每个分组都达到姿态协同的情况称为分组姿态协同。对于这种分组的多航天器系统,文献[19]在无向拓扑上引入了分组一致概念,所设计的控制输入能够使系统渐近达到分组姿态协同,但该研究的结论仅适用于包含2个分组的情况。文献[20]进一步考虑了切换拓扑的情况,通过代换姿态和角速度变量,并对系统Laplacian矩阵进行分解,将分组姿态协同控制问题转化为了稳定性问题,对包含多个分组的多航天器系统构造了控制输入。Weng等对基于SO(3)模型的多分组系统进行了分析,在该研究中,各个分组的领导者能够达到反一致,并且每个分组内的跟随者都能与领导者保持一致,角速度收敛到零[21]。分组姿态协同问题对于多航天器系统的应用具有重要意义,而当前针对该问题的研究仍然不够充分,这一特殊问题可以通过引入分组一致[22-24]的概念来解决。分组一致是指:在包含若干个分组的多智能体系统中,每个分组内部智能体的状态都能达到一致,并且不同分组的一致状态是不同的。
由于目前相关研究仍然有限,本文致力于在分布式事件触发机制下解决多航天器分组姿态协同控制问题,从而减轻系统的通信压力。
1 多航天器系统构建
1.1 航天器姿态模型
考虑一个包含N个航天器及s个分组的系统。航天器按顺序标记为1,2,…,N,分组按照顺序标记为g1,g2,…,gs。每个分组内航天器的数量为ni,并且每个航天器仅能够唯一地被划分到一个分组。采用修正罗德里格斯参数(Modified Rodrigues Parameters,MRP)描述航天器的姿态,以σi(t)∈R3表示航天器的姿态,并以ωi(t)∈R3表示航天器的角速度,于是航天器的姿态运动学和动力学方程可以写为
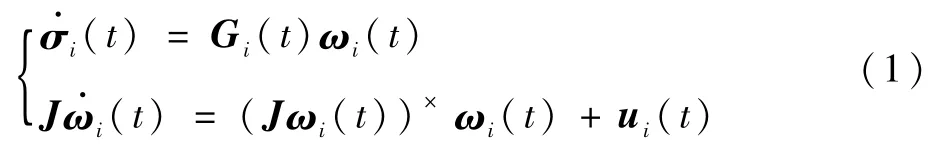
式中:ui(t)∈R3为待设计的航天器的控制输入;矩阵J∈R3×3为航天器的转动惯量,并且本文中假设所有航天器的转动惯量均相同;算子Gi(t)定义为
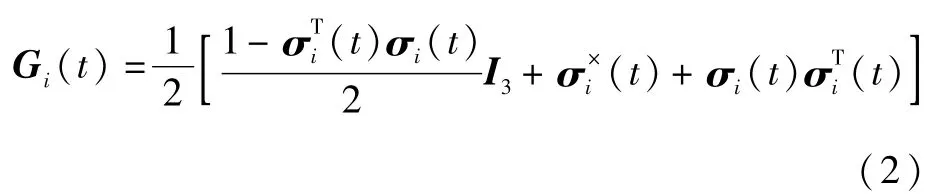
式中:I3为3阶单位矩阵。并定义

对任意一个三维向量x=[x1,x2,x3]T,反对称矩阵x×表示为
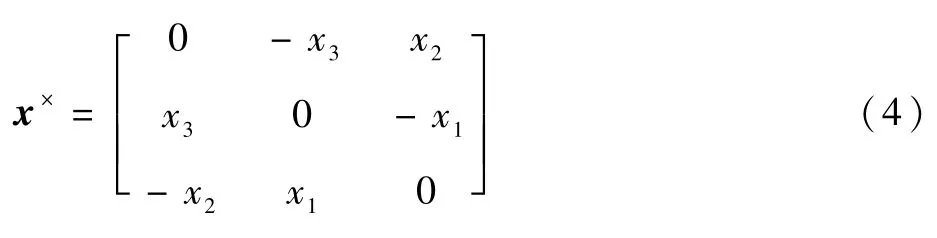
对于分组gk中的航天器i,定义映射Γ(i)=gk。
1.2 系统无向拓扑
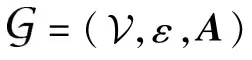
对多航天器的无向拓扑,有如下假设。
假设1每个分组的内部拓扑都是连通的。
假设2对任意2个分组gi和gj,若这2个分组间存在边,那么有且仅有一对节点k,l∈gi和另一对节点m,n∈gj,使得邻接矩阵中元素akm=aln=1以及akn=alm=-1,即这2个分组满足入度平衡[22]。
1.3 分布式事件触发机制
分布式事件触发机制是指:对系统中的每一个航天器i,都设计一个触发函数fi(t)。若在某个时刻满足fi(t)=0,那么航天器i将被触发,并将其姿态和角速度信息发送给邻居。在非触发时刻,航天器之间不进行通信以节省能源和资源。称为航天器i的触发时刻,并且该航天器所有的触发时刻可记为序列…。在时间区间内,控制输入ui(t)为时变值,但仅需考虑航天器自身姿态和角速度的变化。
2 问题描述及主要结果
2.1 控制目的
对于多航天器系统,分组姿态协同的定义如下。
定义1称多航天器达到分组姿态协同,当且仅当系统内航天器的姿态σi(t)和角速度ωi(t)满足:
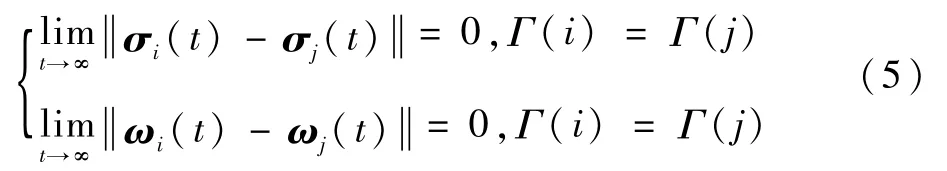
本文的目的在于:在分布式事件触发机制下,设计一种控制输入使多航天器达到如式(5)所定义的分组姿态协同。
2.2 控制输入设计
由于式(1)具有较强的非线性,直接求解分析较为困难,为了降低分析难度,先对式(1)进行转换。受到文献[11]的启发,构造辅助变量si(t)为
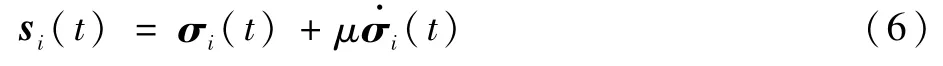
式中:参数μ>0。同时可以得到
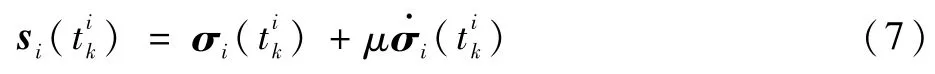
于是航天器的辅助变量误差ei(t)为

根据辅助变量si(t)的定义可知
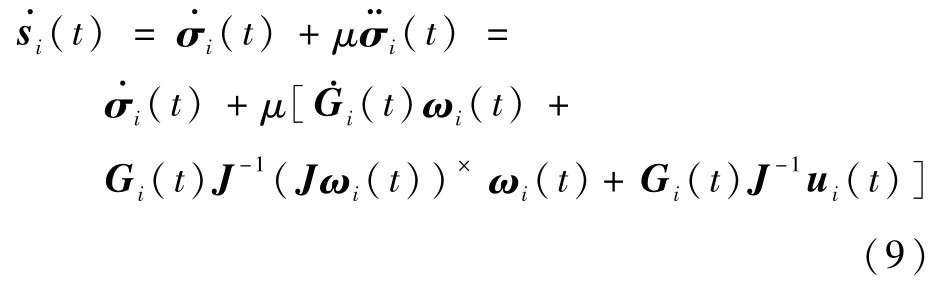
于是可以对航天器i设计控制输入为
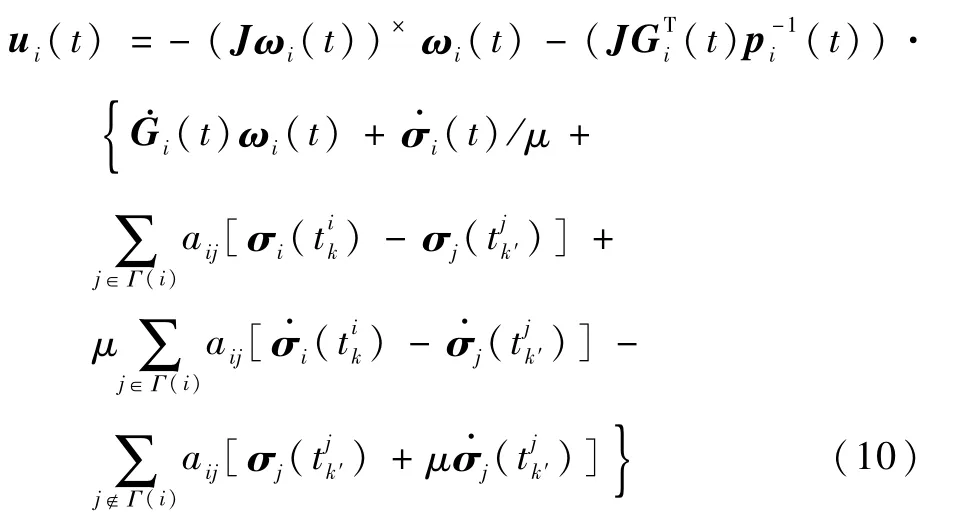
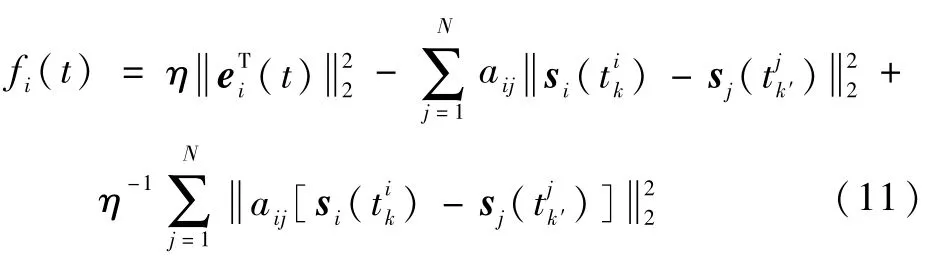
式中:参数η>0为常数。
2.3 控制定理及分析
根据si(t)的定义可知,当
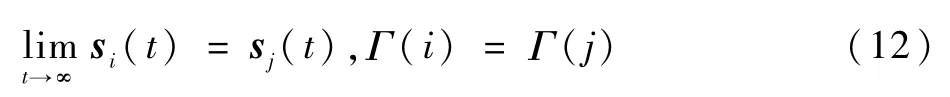
成立时,有
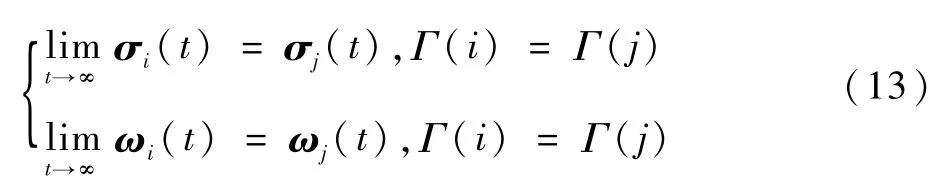
成立,即当变量si(t)达到分组一致时,等价地,多航天器能够达到分组姿态协同。因此,通过分析si(t)的性质可以等价地得到σi(t)和ωi(t)的相关结论。
在上述理论准备的基础上,给出分布式事件触发机制下多航天器分组姿态控制的相关定理及分析。
定理1在分布式事件触发机制下,若多航天器的通信拓扑满足假设1和假设2,并给定控制输入为式(10),设计航天器的触发函数为式(11),则在控制输入的作用下,多航天器能够渐近达到式(5)定义的分组姿态协同。
证明选定Lyapunov函数为

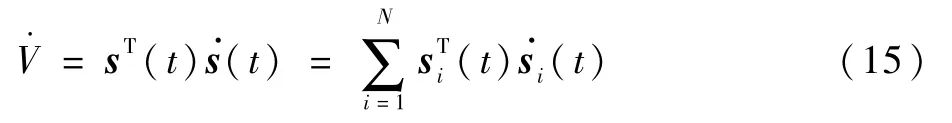
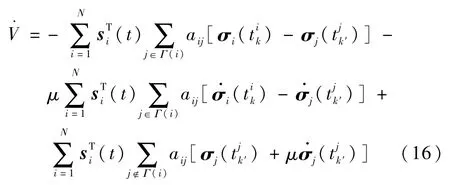
根据假设2,无向拓扑满足入度平衡,因此

于是可知
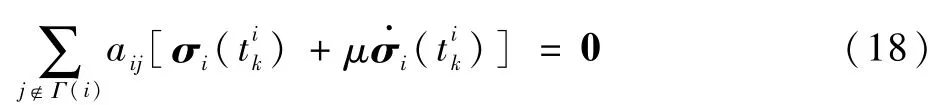
将式(18)代入式(16),V · 可以改写为
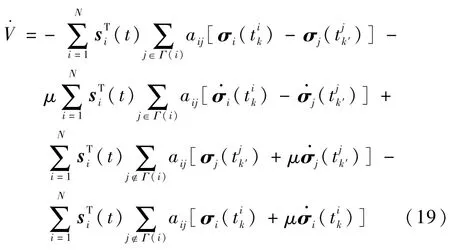
对式(19)进行化简,得到V·为
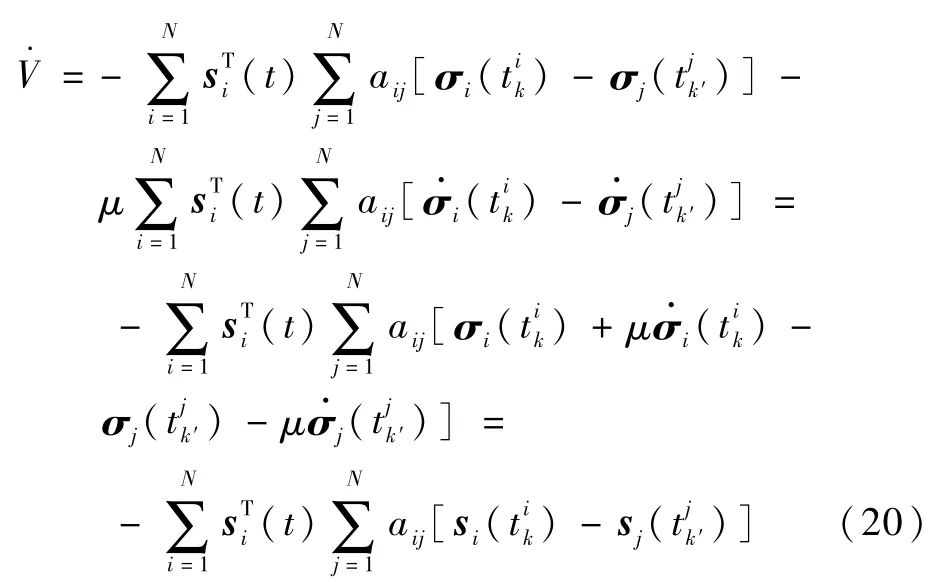
根据辅助误差变量ei(t)的定义,将该误差代入式(20),可以得到
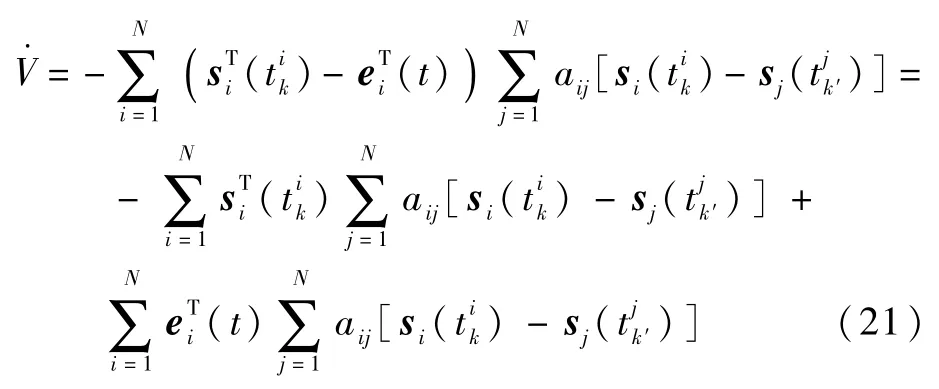
式中:
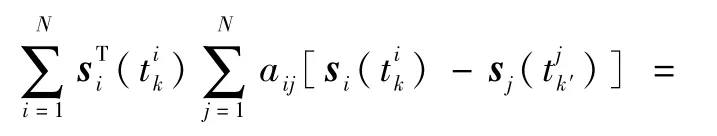
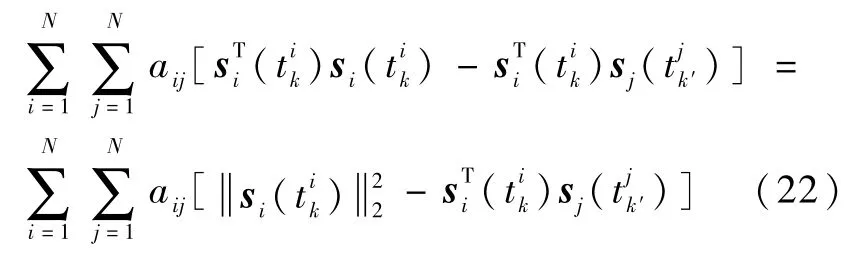
由于无向拓扑的邻接矩阵和Laplacian矩阵都是对称矩阵,即aij=aji,因此有式(23)成立:
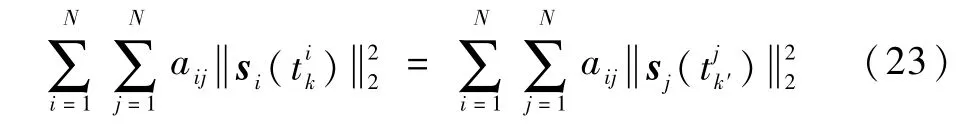
而式(23)意味着式(24)成立:
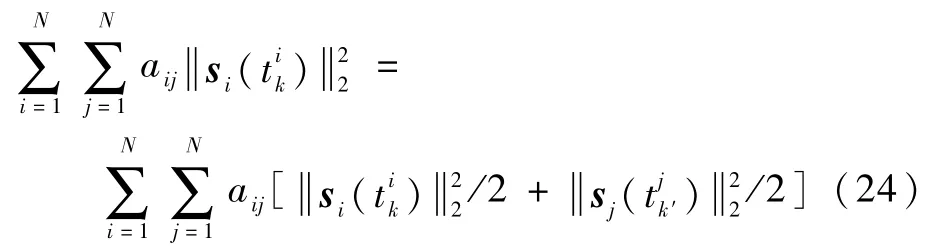
从而可以利用式(24)将式(22)改写为
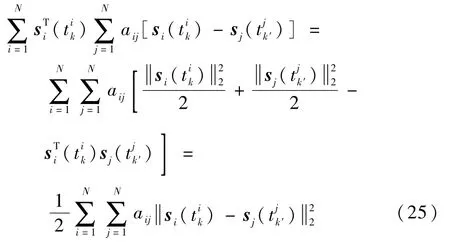
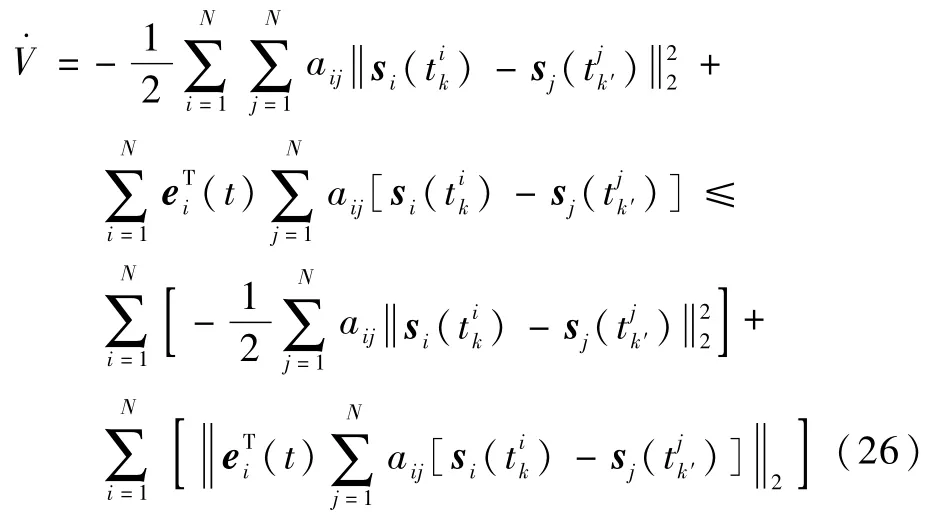
式中:

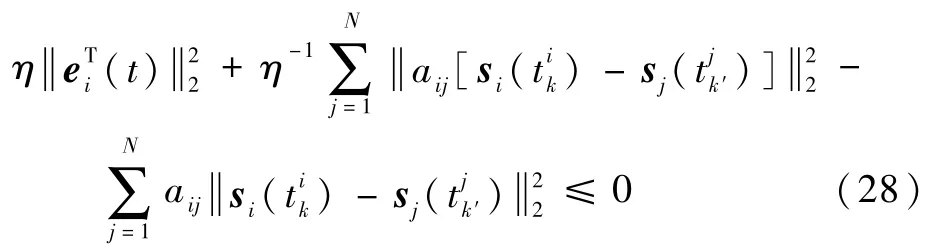
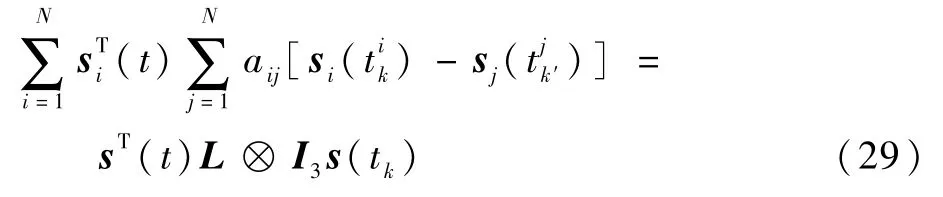
式中:
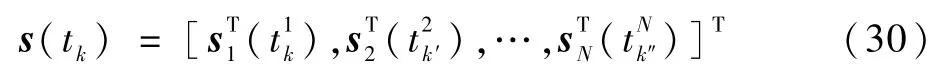
于是根据LaSalle不变原理[25],多航天器系统的解将收敛到集合
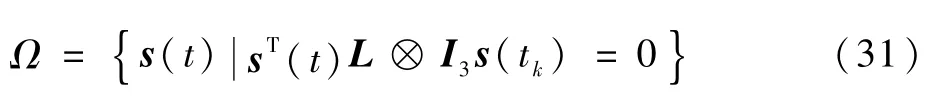
中。而式(31)表明,当t→∞时,总有L⊗I3s(t)=0成立,这意味着对于同一个分组中的航天器i和j,有si(t)=sj(t)。因此可知σi(t)=σj(t),并且有˙σi(t)=˙σj(t),即ωi(t)=ωj(t),此时多航天器达到分组姿态协同。证毕
注1通过分析变量si(t)的性质可知,具有形如式(6)的动力特性的系统是渐近稳定的,从而等价地得到多航天器能够渐近达到分组姿态协同的结论。在分析非线性的式(1)时,这种构造辅助变量的方法能够简化分析过程,降低分析难度。
在事件触发机制下,要避免Zeno现象的发生。Zeno现象是指:某一事件在有限的时间区间内发生的次数是无限的。当系统内发生Zeno现象时,说明航天器将被无限次触发,于是航天器间的通信是连续的,无法达到减少通信次数的目的[26],控制输入失效。因此,对于事件触发机制下的控制方法,有必要分析Zeno现象的存在性并避免其发生。对任意一个航天器分析其是否发生Zeno现象,即可推广到整个多航天器系统。
定理2在分布式事件触发机制下,给定航天器的控制输入为式(10),事件触发函数为式(11),则系统内任意一个航天器不会发生Zeno现象。

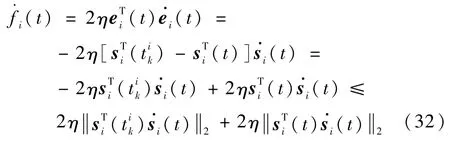
式中:
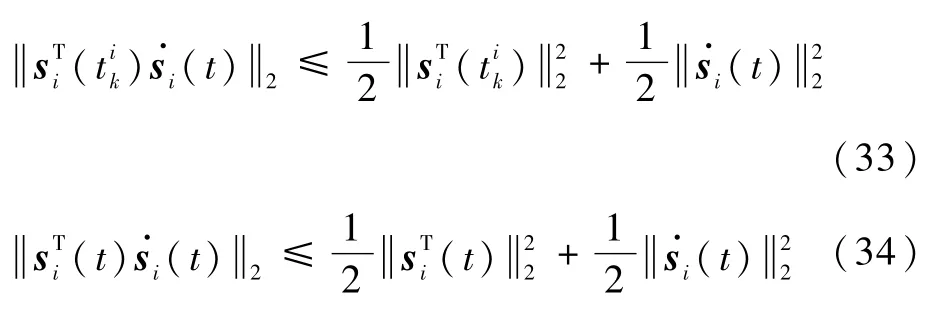
于是可知
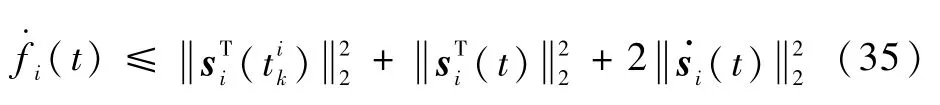
定义κ为
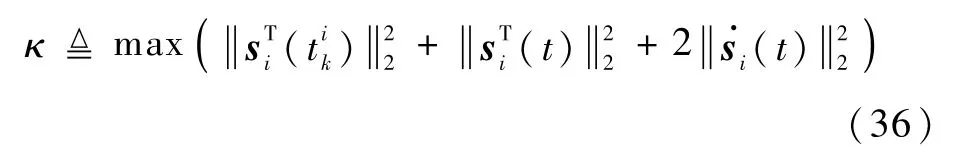
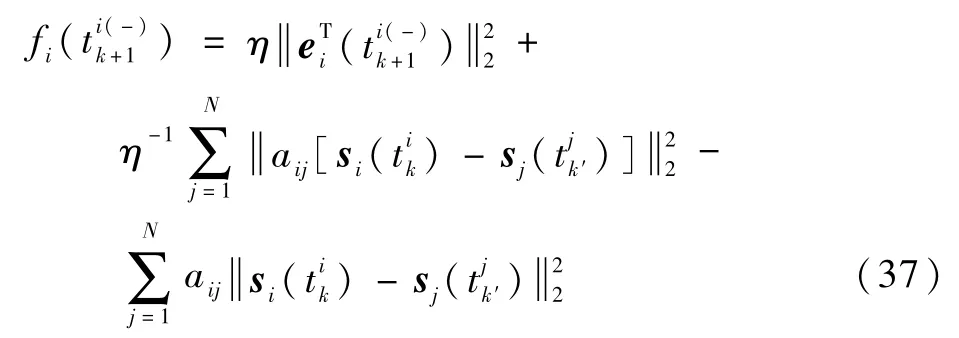
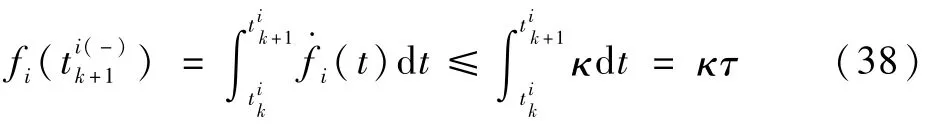
3 仿真结果与验证
为了验证本文在分布式事件触发机制下提出的控制输入的有效性,构造一个包含9个航天器及2个分组的系统进行仿真。航天器按照顺序标记为1,2,…,9,并且航天器1~4组成分组g1,航天器5~9组成分组g2。多航天器的无向拓扑如图1所示。可以看出,该无向拓扑满足假设1和假设2。
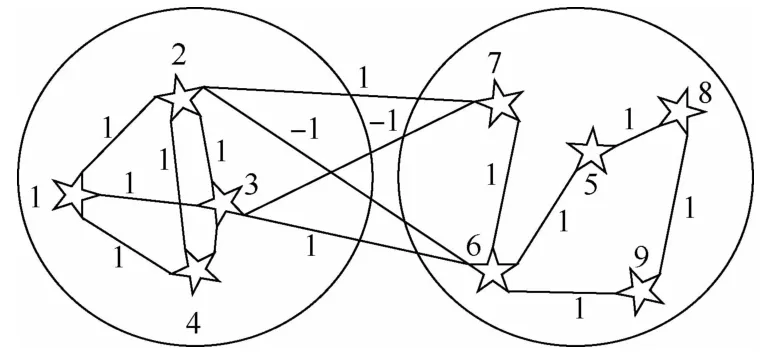
图1 多航天器的无向拓扑Fig.1 Undirected topology of multi-spacecraft
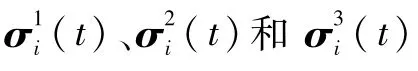
航天器的角速度时间响应如图3所示。纵坐标上角标的意义与图2中相同。根据图3中的结果所示,系统中所有航天器的角速度最终都收敛到零,这与图2中的姿态曲线相吻合。图2和图3说明,在本文提出的控制输入的作用下,最终多航天器达到静态的分组姿态协同。
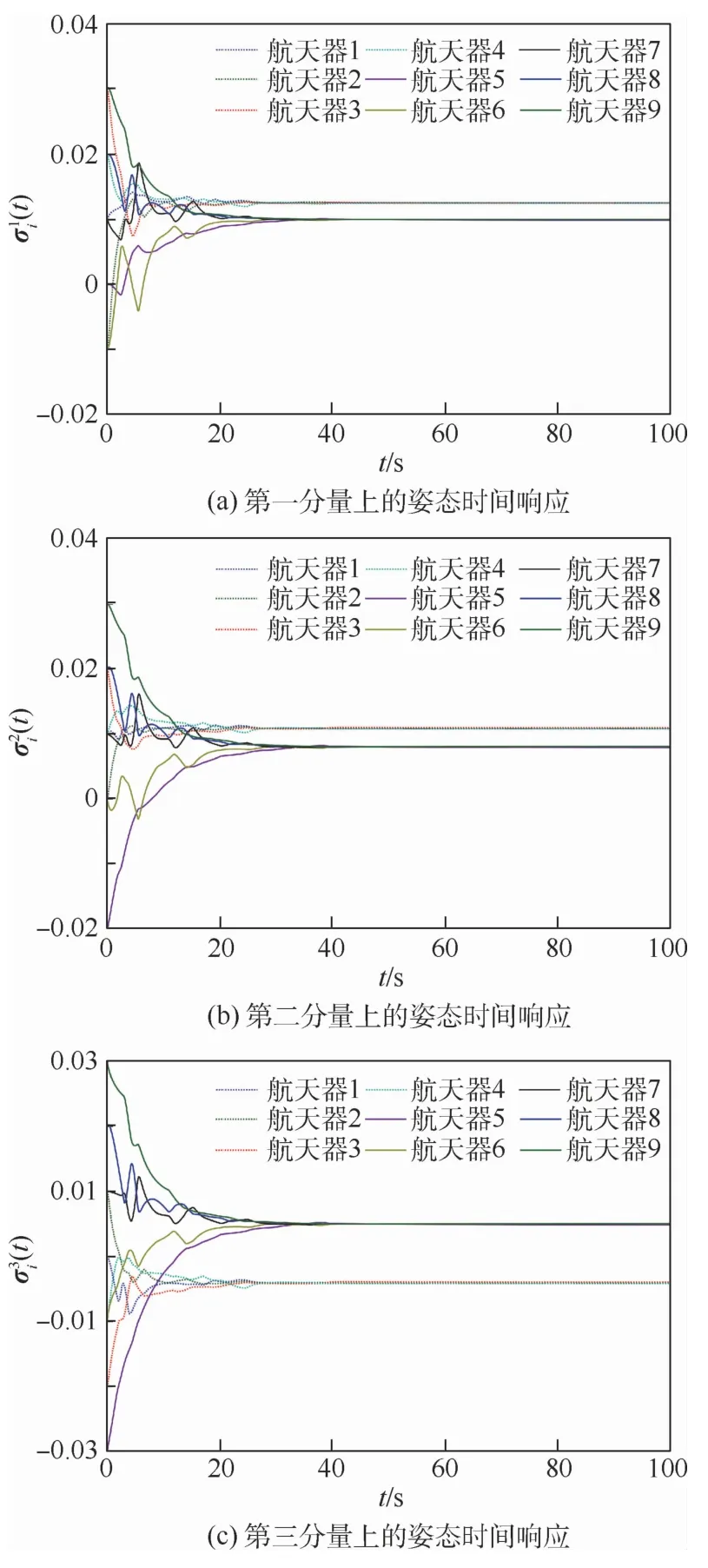
图2 航天器在3个分量上的姿态时间响应Fig.2 Attitude time response of spacecraft on three components
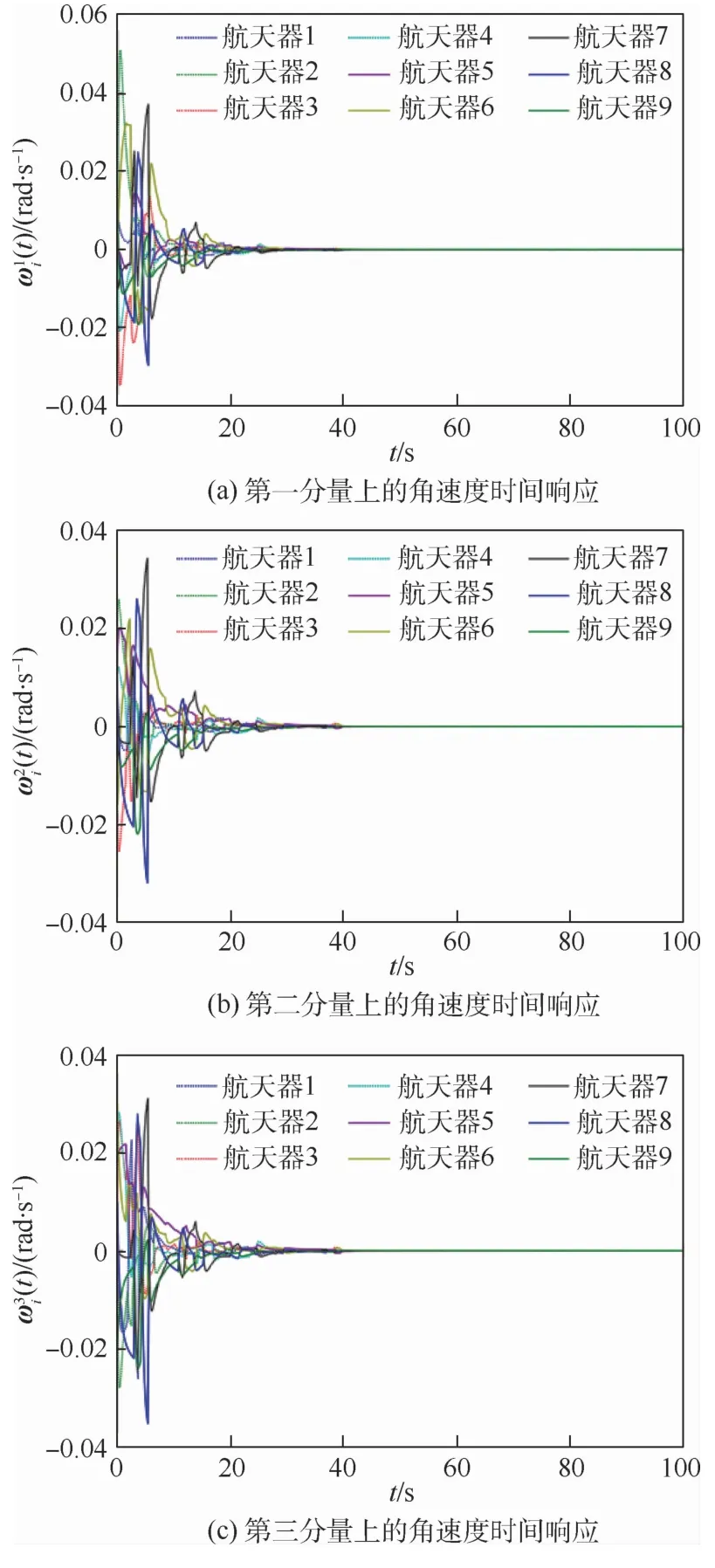
图3 航天器在3个分量上的角速度时间响应Fig.3 Angular velocity time response of spacecraft on three components
下面对文献[16]中不采用事件触发机制的研究进行复现,航天器的姿态时间响应和角速度时间响应分别如图4和图5所示。图4和图5中的结果显示,在文献[16]中控制输入的作用下,多航天器也达到了静态的分组姿态协同。

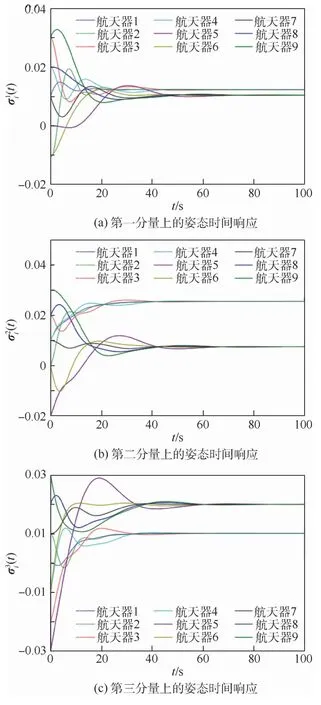
图4 文献[16]中航天器在3个分量上的姿态时间响应Fig.4 Attitude time response of spacecraft on three components in Ref.[16]
引入分布式事件触发机制的目的在于减少航天器间的通信次数,节约计算和通信资源。对9个航天器的触发次数、最小时间间隔和最大时间间隔进行统计,所得结果如表1所示。
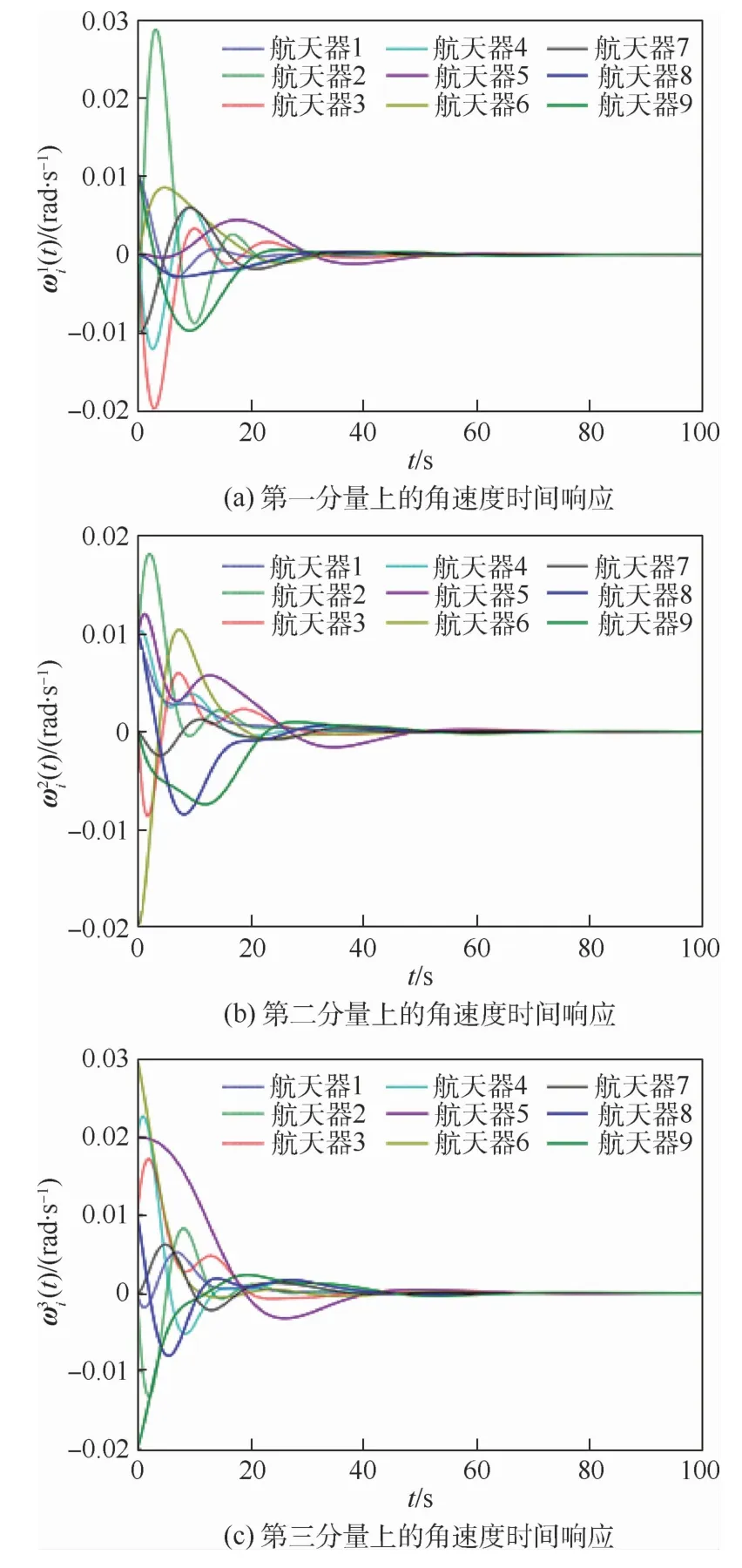
图5 文献[16]中航天器在3个分量上的角速度时间响应Fig.5 Angular velocity time response of spacecraft on three components in Ref.[16]
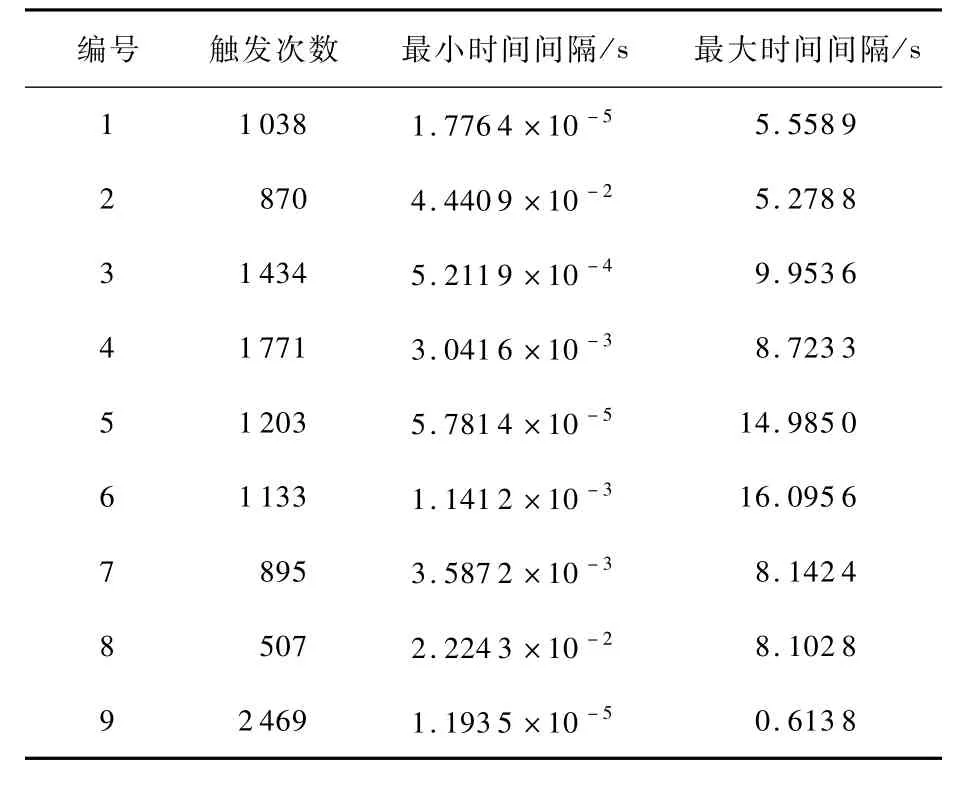
表1 触发结果统计Table 1 Statistical triggering result
根据表1中的结果可知,尽管系统内航天器的最小触发时间间隔都较小,但仍然严格大于零,而最大触发时间间隔达到了16.095 6 s。表1中的结果表明,每个航天器的触发时间间隔与定理2是相吻合的,不会发生Zeno现象。
图2和图3中对小角度初值的情况进行了仿真,航天器的初始姿态和初始角速度数值较小,并且与2个分组最终的协同姿态和协同角速度接近。下面对大角度初值的情况进行仿真,进一步验证本文设计的控制方法的有效性。
图6和图7中的仿真结果表明,在大角度初值的条件下,2个分组内的航天器的姿态都分别达到了协同,并且所有航天器的角速度都收敛到零,因此多航天器仍然能够达到分组姿态协同。分别对比图2和图6,以及图3和图7,可以看出,在大角度初值的情况下,多航天器达到分组姿态协同所需的时间更长,并且由于初始姿态和处置角速度的值较大,2个分组的协同姿态和协同角速度间的差值也更大。
仿真结果和对比分析表明,在分布式事件触发机制下,本文提出的控制输入是有效的。
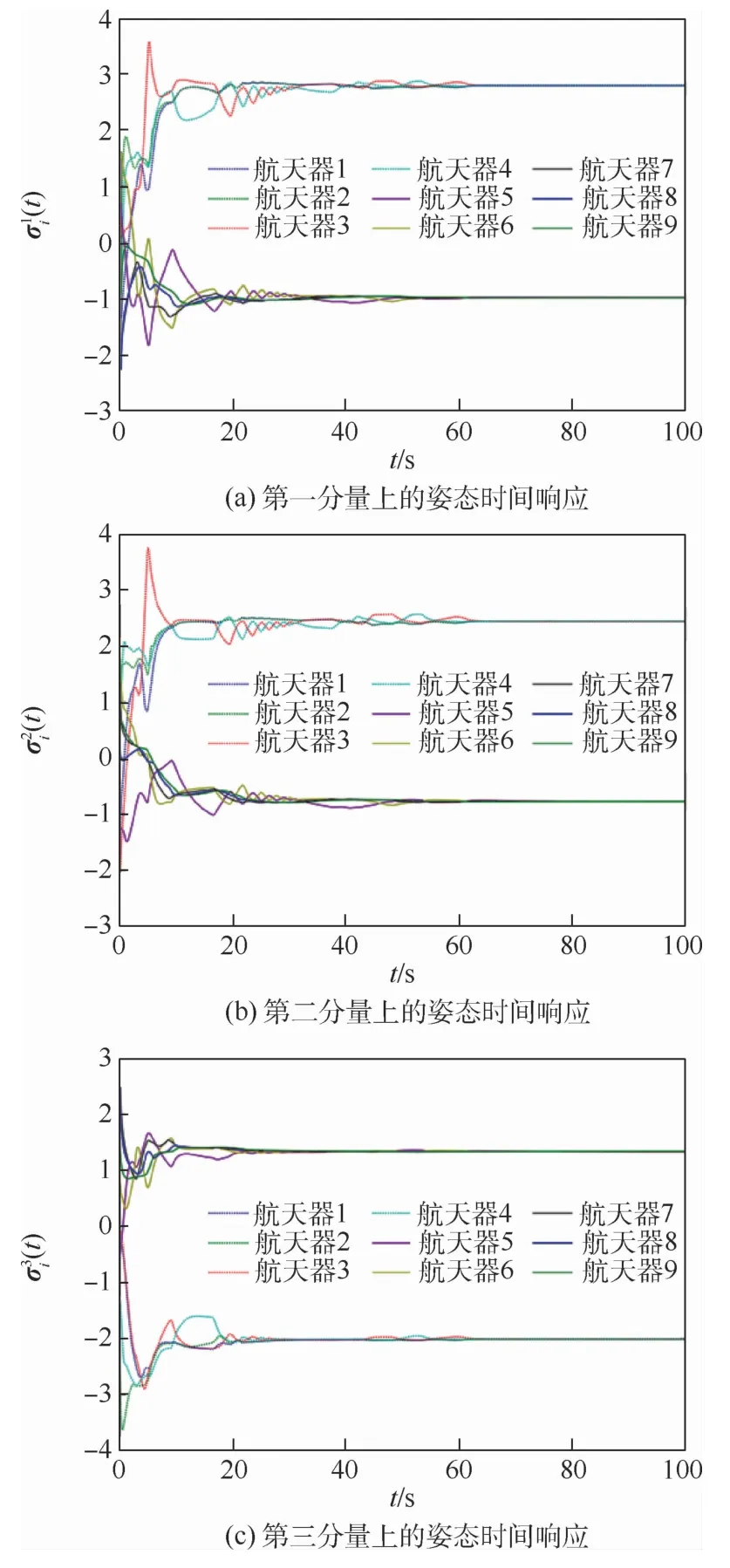
图6 大角度初值条件下航天器在3个分量上的姿态时间响应Fig.6 Attitude time response of spacecraft on three components with large initial angles
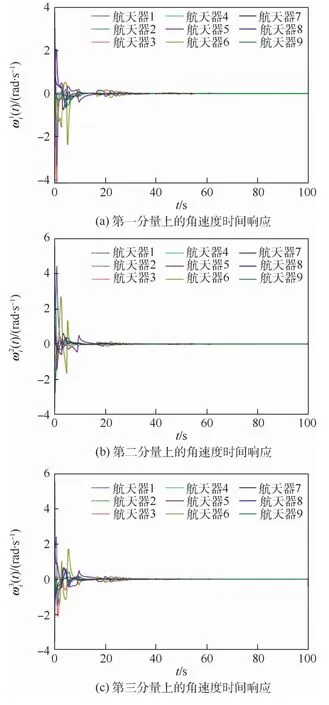
图7 大角度初值条件下航天器在3个分量上的角速度时间响应Fig.7 Angular velocity time response of spacecraft on three components with large initial angles
4 结 论
本文在分布式事件触发机制下研究了多航天器分组姿态协同控制问题。具体结论如下:
1)考虑了包含多个分组的多航天器系统,采用MRP描述航天器的姿态,通过构造辅助变量,设计了分布式的控制输入,并且控制输入不依赖辅助变量;航天器的事件触发函数中仅需要邻居的辅助变量信息,因此也是分布式的。
2)假设2引入了入度平衡的概念,结合代数图论和Lyapunov稳定性理论说明了建立在si(t)上的系统能够渐近达到分组一致,从而等价地得到多航天器渐近达到分组姿态协同的结论,并说明了系统不会发生Zeno现象。
3)仿真结果以及与现有文献的对比表明,本文提出的控制输入能够使多航天器达到静态的分组姿态协同,并且每个航天器的最小触发时间间隔都严格为正,与定理2相吻合。
由于本文考虑的航天器姿态动力学和运动学方程为理想状态,后续将进一步考虑更复杂的条件。

