一种基于模糊控制的平稳滑翔再入制导律

周锐，张宇航，熊伟，史智广

（1.北京航空航天大学 自动化科学与电气工程学院，北京100083；2.中国电子科技集团公司航天信息应用技术重点实验室，石家庄050081；3.北京航天长征飞行器研究所，北京100076； 4.北京宇航系统工程研究所，北京100076；5.北京临近空间飞艇技术开发有限公司，北京100070）

临近空间内的某型升力式高超声速飞行器（Lifting Hypersonic Vehicle，LHV）相较于传统飞行器，具有航程远、速度快等难以比拟的优势。然而，高超声速飞行器的再入环境复杂，气动模型具有极大不确定性，同时面临多飞行约束及动力学方程的强非线性问题，故高超声速飞行器的再入制导律设计也成为了当前各国空天领域研究的重点与难点［1-4］。

再入过程中大气环境变化剧烈，升力式高超声速飞行器的滑翔轨迹会呈现一种周期性振荡现象，这种振荡使得飞行器容易超出过程约束及准平衡滑翔条件（Quasi-Equilibrium Glide Condition，QEGC）的限制，严重影响了系统的稳定性。因此，有效消除振荡现象、保证再入滑翔过程的平稳性成为了目前再入制导的重点问题。文献［5］提出了一种基于QEGC的自适应制导方法，利用QEGC的特定弹道形式对末端速度及射程进行解析预测，修正倾侧角及迎角，使得弹道平滑。文献［6］通过QEGC将高度-速度平面内各项再入约束形成的飞行走廊转换为倾侧角-速度空间内的倾侧角走廊，通过在倾侧角走廊内设计倾侧角指令曲线来生成满足飞行走廊约束的标准轨迹。以上2种方法均以QEGC为基础，前者不依赖于标准轨迹，但需修正迎角指令，这使得纵向航程及升力受到影响，后者依赖于标准轨迹，自适应能力及鲁棒性一般，且由文献［7］可知，QEGC在航迹角增大或低速情况下可能失效。考虑到以上因素，文献［8］提出了一种不依赖于QEGC的再入制导律，设计一种参数化的反馈控制律，根据高度变化率实时修正倾侧角幅值，有效抑制了周期性振荡现象，该方法无需修正迎角指令，减小了对升力的影响，但控制效果一定程度上依赖于参数设计，需要经过对参数的不断修正才能提升。

针对现有方法的不足，本文结合模糊控制不依赖于模型、构造容易、鲁棒性和自适应能力好的优点，在充分考虑各种约束的前提下，设计了基于模糊控制的升力式高超声速飞行器的平稳滑翔再入制导律。

1 再入制导问题

1.1 三自由度运动学方程

为了方便滑翔再入制导律的设计，在考虑地球自转、忽略地球扁平率及风影响的条件下，于半速度坐标系建立升力式高超声速飞行器的三自由度再入模型［9］：

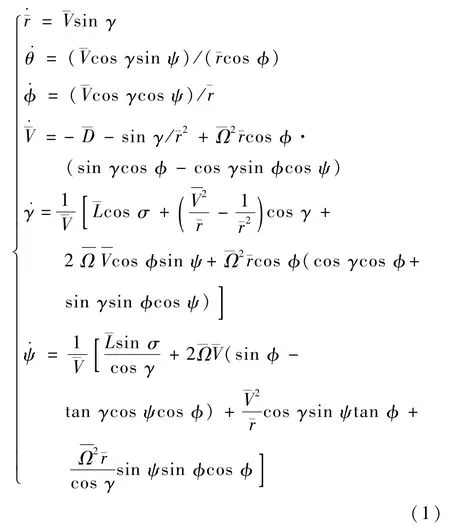
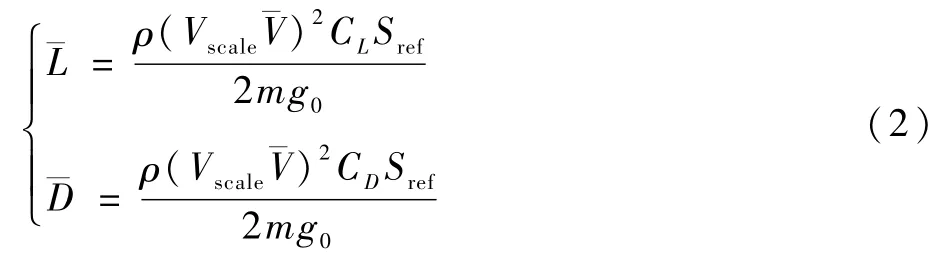
式中：ρ0为海平面标准大气密度；Kρ为大气密度系数；h为海拔高度。

1.2 气动参数处理

本文着重于制导律的设计研究，故假设再入滑翔过程中飞行器力矩平衡，此外飞行器采用倾斜转弯的方式，故可以忽略侧力影响。

由式（2）可得，飞行器再入飞行过程中无量纲化升力加速度¯L和阻力加速度¯D的大小与升力系数CL和阻力系数CD有关，而CL与CD为非常值的气动参数，其大小由以下参数决定［11］：

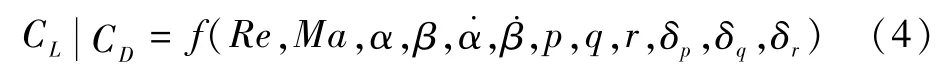
式中：Re为雷诺数；Ma为马赫数；α和β分别为迎角和侧滑角；p、q、r分别为机体三轴旋转角速度；δp、δq、δr分别为机体三轴舵偏角。

式（4）经过合理简化后，最终形式如下［12］：

由式（5）可知，在一定条件下，CL与CD的值需要输入迎角α、马赫数Ma及侧滑角β通过查表确定。为提高效率，在零侧滑条件下，可以假设正常飞行状态时CL与CD对应马赫数Ma与迎角α的函数关系式为

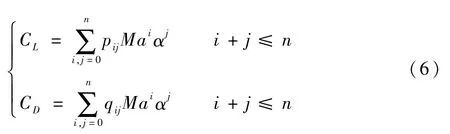
式中：pij和qij为多项式系数。

为保证精度，这里设置多项式阶数n=4，借助已有的公开数据［13］可以得到近似函数中的多项式系数。

对于升力式高超声速飞行器，再入飞行过程中受到热流密度Q、过载nLD、动压q等约束的限制，具体表述如下［14］：

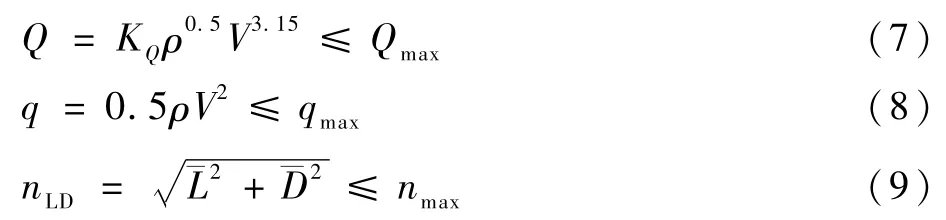
式中：KQ为热传递系数；Qmax、qmax和nmax分别为飞行器所能承受的热流密度、动压和过载的最大幅值。

式（7）～式（9）组成了再入过程的强约束条件。

1.3 终端约束

本文采用能量e作为微分方程的自变量［15］：

滑翔段的飞行任务是保证飞行器能顺利进入末制导阶段，因此，终端约束主要包括高度速度约束及经纬度约束：

式中：ef为终端能量约束；hf、Vf、θf和φf分别为再入终端的高程、空速、经度和纬度值。

1.4 H-V再入走廊

为了抑制高超声速飞行器再入滑翔过程中的周期性振荡现象，再入制导方法中常引入QEGC［16］：

QEGC可视作再入过程的软约束条件，结合3个强过程约束条件可以转化为H-V再入走廊的上下界［16］：

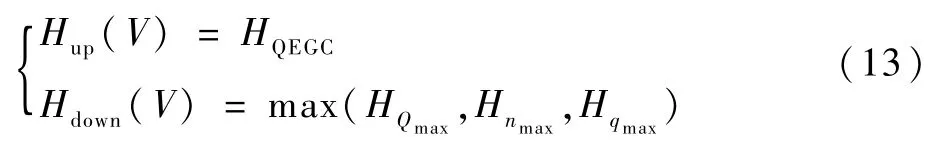
式中：Hup（V）、Hdown（V）分别为H-V剖面的上、下边界。

由此可以得到H-V再入走廊如图1所示。

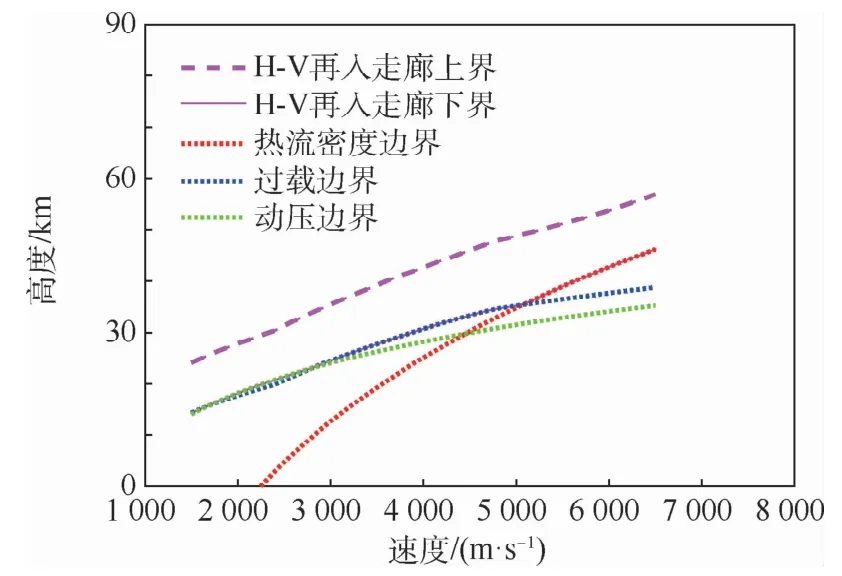
图1 H-V再入走廊Fig.1 H-V reentry corridor

2 平稳滑翔再入制导

2.1 纵向制导律设计

考虑到再入飞行器初始下降段的热保护要求，迎角指令常采用工程中应用较多的三段式迎角剖面［17］：

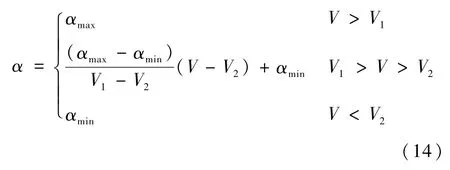
式中：αmax、αmin为再入迎角边界值；V1、V2为迎角剖面临界速度。

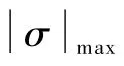
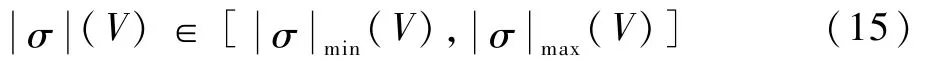
因为再入点初始高度较高，气动力作用较弱，QEGC难以满足，故以常值倾侧角作为初始控制指令，其方向由再入点与目标点的视线角Δψ0=ψT0-ψ0决定，即

式中：ψT0为再入点到目标点的航向角；ψ0为初始航向角。

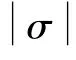
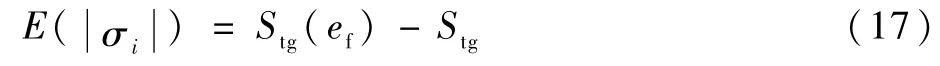
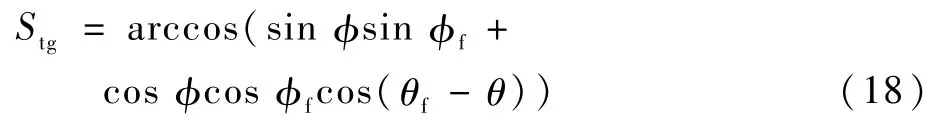
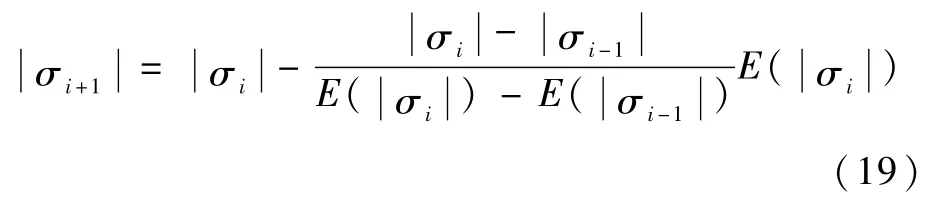
2.2 横侧向制导律设计

横侧向制导决定倾侧角符号，即偏转方向。这里考虑到再入段不同位置机动能力的区别，设计如下航向角误差走廊，主要通过目标视线角Δψ=ψT-ψ确定偏转方向［20］。

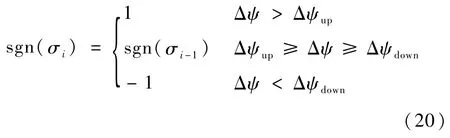
式中：Δψup、Δψdown分别为视线角上、下界。

采用一种漏斗型走廊以适应不同高度下飞行器气动效能的变化，如图2所示。

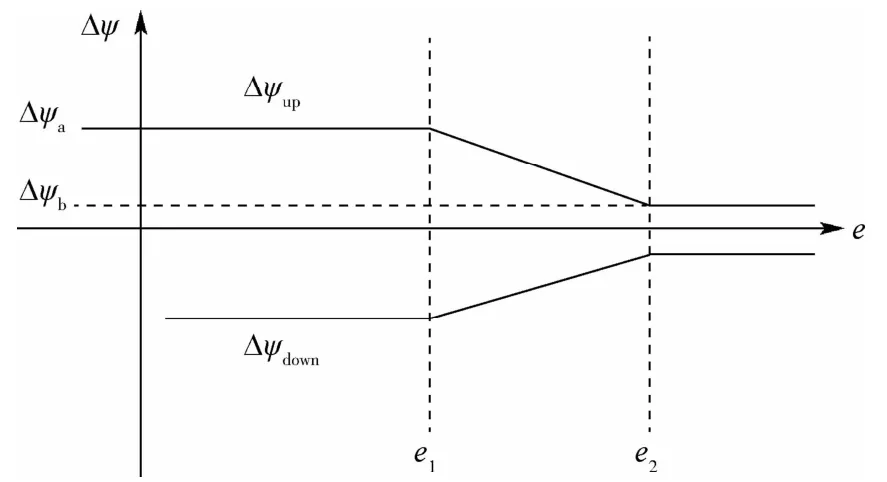
图2 航向角误差走廊Fig.2 Course angle error corridor

视线角上、下边界值Δψup与Δψdown由式（21）获得：

式中：Δψa、Δψb为视线角边界参考值；e1、e2为能量临界值。

2.3 平稳滑翔模糊制导律

结合模糊控制原理在倾侧角外环控制回路增加反馈控制量，对横侧向制导通道输出指令幅值进行实时调节来达到抑制振荡，保持平稳滑翔。

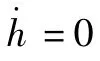
模糊控制器输出的倾侧角调节量Δσfuzzy线性叠加到预测校正制导律的输出上：

在确定系统输入、输出与基本结构后，下面分别介绍各部分的设计。

1）输入、输出论域定义

图3 基于模糊控制的倾侧角调节算法Fig.3 Bank angle correction algorithm based on fuzzy control

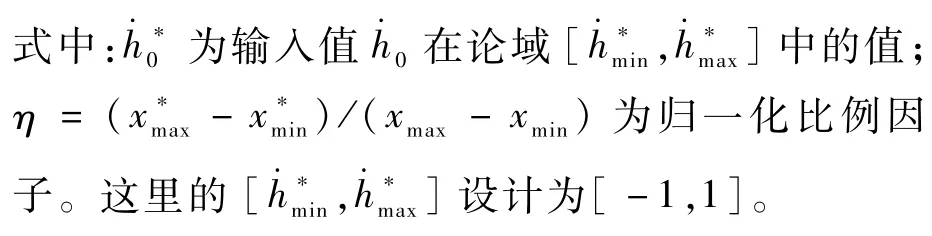
2）输入、输出隶属度函数

输入、输出变量的模糊等级均采用8级：“NB、NM、NS、NE、PE、PS、PM、PB”，分别代表自然语言中“负值很大、负值较大、负值较小、负值很小、正值很小、正值较小、正值较大、正值很大”。模糊隶属度函数选用三角形，输入V、和输出Δσfuzzy的隶属度函数均可表示为图4。

图4 输入、输出隶属度函数Fig.4 Membership function of input and output

3）模糊规则设计

根据以上分析可以设计以下模糊推理规则，如表1所示。

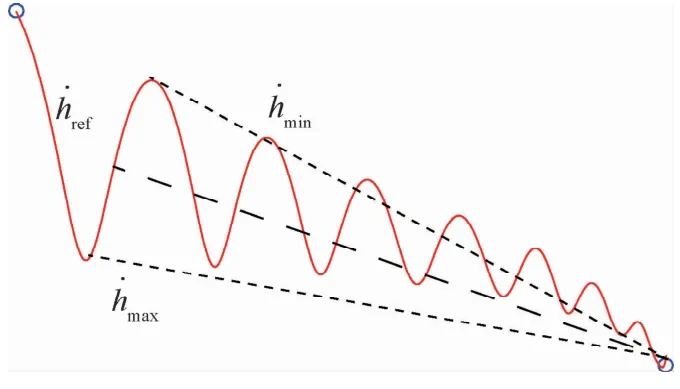
图5 参考高度变化率取值Fig.5 Reference value definition of height gradient

表1 模糊推理规则Table 1 Fuzzy logic rules

4）解模糊

由模糊规则可得当前输入下输出值Δσfuzzy的各模糊等级隶属度，要计算其在论域的取值还需要进行解模糊操作，采用重心法：

式中：G为重心位置，即输出在论域［0，1］的取值；gi为每个三角形隶属度函数的重心；Si为每个模糊等级的隶属度；N为模糊等级数。

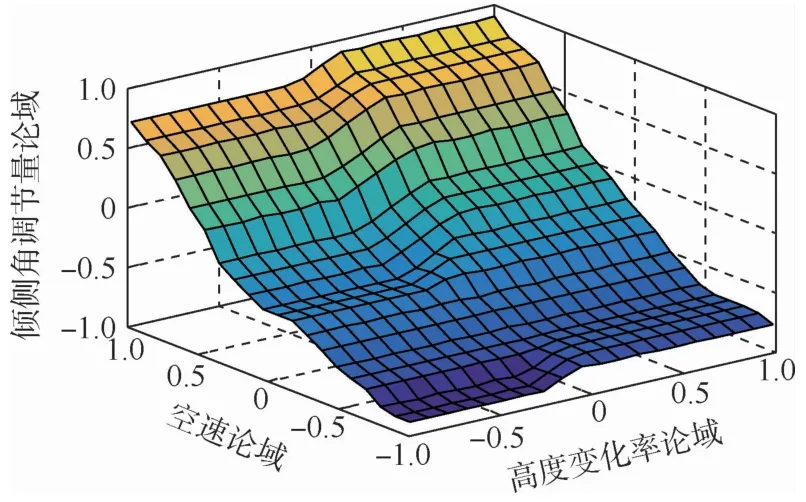
图6 倾侧角修正值模糊推理结果Fig.6 Fuzzy logic results of bank angle correction

模糊平稳滑翔制导律设计流程如图7所示。

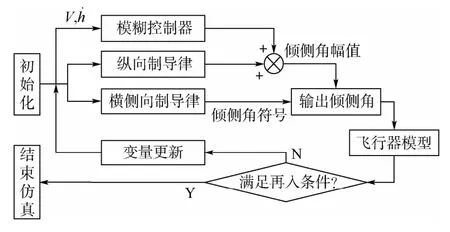
图7 基于模糊控制的平稳滑翔再入制导律Fig.7 Reentry steady glide guidance algorithm with fuzzy control

3 仿真验证

以某型号升力式高超声速飞行器为研究对象，由公开数据，其质量m=907.2 kg，机翼参考面积Sref=0.483 9 m2，机体所能承受最大热流密度Qmax=1 000 kW/m2，最大动压qmax=500 kPa，最大过载nmax=4g。

对于本文方法仿真的精度，要求落点误差不大于15 km，大于15 km的认为任务失败，高度误差不大于2 km，速度误差在100m/s以内。

对于制导指令输出，要求倾侧角幅值不超过σmax=80°，迎角均为正且不超过αmax=20°。

仿真中，微分方程采用四阶龙格库塔法积分。

3.1 标准条件下再入制导仿真

设置3个不同初始条件，如表2所示。终端约束相同的仿真算例，每个条件下分别对传统预测校正法和基于模糊控制的平稳滑翔再入制导律进行仿真验证，用以测试模糊规则及倾侧角反馈控制对再入周期性振荡的抑制效果。

2种制导律下分别进行仿真验证，得到的末端误差如表4所示，其中，“/”号前后值分别代表预测校正法和本文制导律下的误差值。

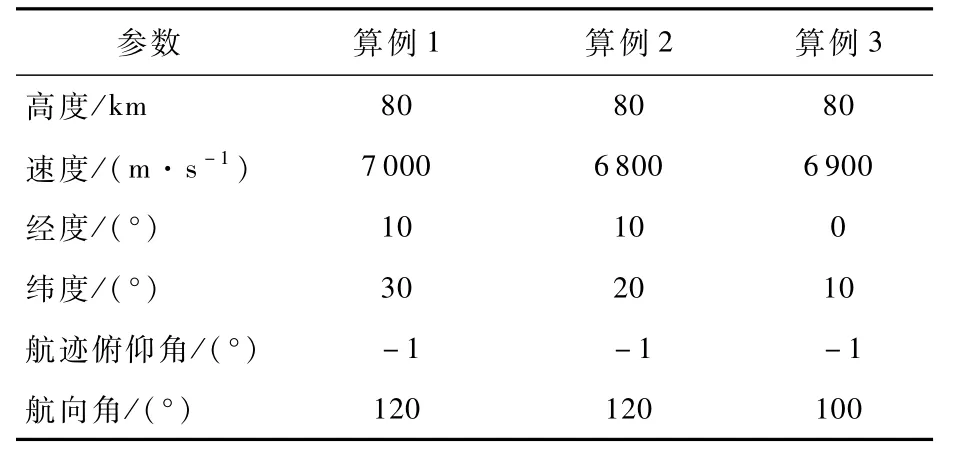
表2 标准条件下再入初始参数Table 2 Reentry initial parameters in standard conditions

仿真结果如图8所示，图中左侧为本文制导律下的再入制导仿真曲线，右侧为传统预测校正法的再入制导仿真曲线。

表3 标准条件下再入末端约束Table 3 Reentry terminal constraint in standard conditions

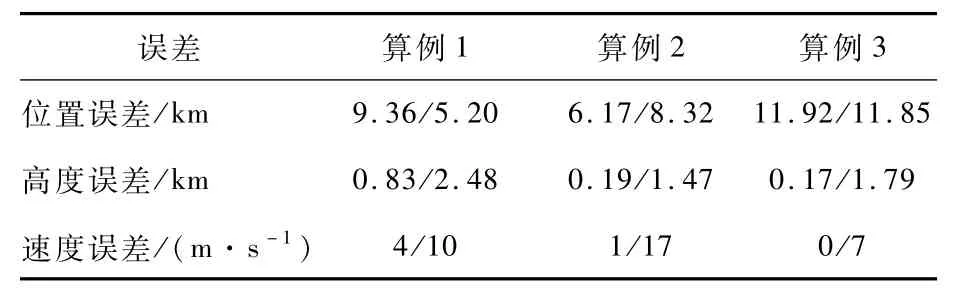
表4 标准条件下再入末端误差Table 4 Reentry terminal error in standard conditions

图8 标准条件下的再入制导仿真结果Fig.8 Simulation results of reentry guidance in standard conditions

对比图8曲线及表4所示终端误差结果，可以得到以下结论：

1）由表4可得，本文制导律满足再入制导精度要求，落点距离误差小于15 km，高度误差小于2 km，速度误差小于100m/s，且在高度及速度误差上均要优于传统预测校正法，说明了轨迹的平稳对于末端能量管控的重要作用。

2）从图8（a）再入三维轨迹可以看出，包含倾侧角指令调节的平稳滑翔再入制导律有效抑制了从第一个拉起段之后的周期性振荡，使得再入过程相较于传统预测校正法的再入制导仿真曲线更加平稳，达到了预期目标。

3）从图8（b）可以看出，本文制导律保证了再入轨迹完全位于H-V再入走廊内部，即满足QEGC、热流密度、动压及过载约束，而传统预测校正法的再入制导仿真曲线则出现多个振荡且峰值超出H-V再入走廊约束（QEGC约束条件）。

4）从图8（c）可以看出，本文制导律倾侧角指令曲线在1 500 km处出现较大幅值，对应于第一个拉起段，表明了模糊控制器调节效果明显，在满足指令幅值约束的条件下抑制了振荡。

3.2 扰动条件下再入制导仿真

为了验证本文方法在扰动条件下的鲁棒性，采用Monte Carlo再入制导仿真实验。在该实验中，保持飞行器参数不变，对初始位置及气动参数（升阻力系数）设置扰动，如表5所示。

再入制导初始参数如表6所示。

表5 再入扰动参数设置Table 5 Dispersion parameter setting of reentry guidance

再入制导末端约束如表7所示。

表6 扰动条件下再入初始参数Table 6 Reentry initial parameters in dispersion conditions

表7 扰动条件下再入末端约束Table 7 Reentry terminal constraint in dispersion conditions

按照以上参数进行100次Monte Carlo仿真，得到仿真结果如图9所示。分别从振荡抑制效果、终端误差及过程约束方面展示了制导律的性能，对此进行分析可得如下结论：

1）在存在初始偏差及参数误差的情况下，本文制导律可满足制导精度要求，速度误差不大于100m/s，高度误差不大于2 km，末端位置误差在10 km内的占97%，在5 km内的占66%，CEP小于5 km。

2）由图9（a）～图9（c）可以看出，在存在扰动的情况下，基于模糊控制的倾侧角调节策略可有效抑制周期性振荡，所有再入轨迹均未出现波动情况，整个飞行过程趋于平稳，说明本文方法的自适应性及鲁棒性较强。

3）从图9（d）可得，整个滑翔过程倾侧角指令反转次数大约为3～4次，且反转的射程间距大于200 km，保证了指令的有效性，说明基于能量分段的航向角误差走廊在满足大横程机动性要求的前提下有效减少了反转次数。

4）速度-高度轨迹及过程约束、再入滑翔过程满足QEGC及热流密度、动压和过载约束，整个滑翔段都位于H-V再入走廊内部，保证了飞行的稳定性和强约束要求。

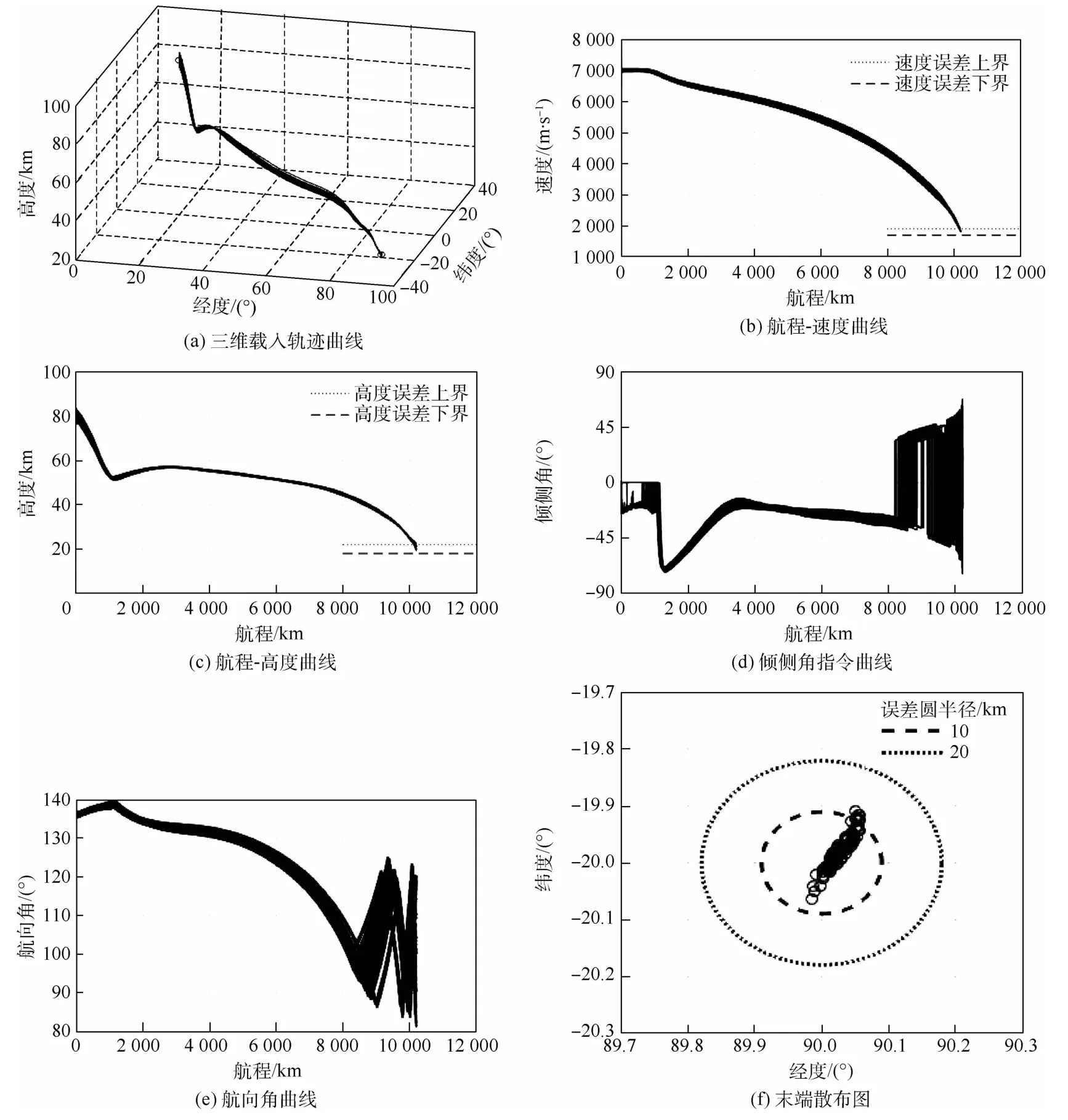
图9 扰动条件下的再入制导仿真结果Fig.9 Simulation results of reentry guidance in dispersion conditions

4 结 论

本文针对升力式高超声速飞行器再入滑翔过程中的周期性振荡问题，基于模糊推理控制及预测校正法提出了一种倾侧角反馈调节策略，经过研究分析及仿真验证，得到以下结论：

1）基于模糊控制的平稳滑翔再入制导律不依赖QEGC，适应能力更强，避免了再入航迹俯仰角增大或空速较低等条件下的QEGC失效问题。

2）倾侧角指令调节通过模糊控制器实现，可以充分考虑当前飞行状态，更加准确地输出指令幅值调节量。本文方法不需要设计反馈控制回路参数，避免了参数设计需要的大量样本和时间。

3）相较于传统预测校正制导，本文方法在满足精度要求的前提下有效抑制了振荡，且具有良好的鲁棒性和自适应能力。