基于随机机动模型和落点预测的制导律设计

杨庶

（西北工业大学 自动化学院，西安710072）

对于非自旋弹体的制导武器，比例制导律是一种有效且广泛使用的制导律［1-2］。但对于自旋弹体而言，该制导律有可能出现制导性能下降、落点误差增大等问题［3］。为了提高自旋弹体的制导性能，迫击炮弹［4］、制导炮弹［5-8］、火箭弹［9-11］等自旋弹体采用了基于落点预测的制导律。这种制导律一般需要根据弹体的气动参数和运动方程，通过常微分方程数值求解方法在线求解落点预测值，通过落点预测值与目标间的偏差生成制导指令。显然，气动参数和弹体运动方程的精度和复杂程度越高，落点预测值的精度越高，在线计算的成本也越大［12］。

国内学者在基于落点预测的制导律设计方面开展了大量的研究。普承恩等［13］根据弹箭质点模型，考虑气动参数对弹道的影响，采用扩展卡尔曼滤波方法预测落点偏差并生成制导指令。杨泗智等［14］针对高旋火箭弹，采用保留弹体滚转动力学方程的四自由度修正质点模型，预测火箭弹落点并生成弹道修正控制量。钟扬威等［15］基于扩展质点弹道模型，通过2次落点预测（即一次弹体无控状态的落点预测和一次弹体有控状态的落点预测），设计了一种用于旋转稳定弹体的二维落点预测制导方法。何子达等［16］根据弹体气动参数，建立了二维弹道修正弹的有控滤波模型，采用扩展卡尔曼滤波方法预测落点，进而生成弹道修正指令。赵江等［17］考虑了禁飞区对航迹的约束条件，根据飞行器三自由度运动方程，采用落点误差预测和指令校正相结合的方法，修正飞行器纵向航迹。王青等［18］根据飞行器气动参数，建立了以能量为自变量的飞行器再入模型，设计了满足再入约束条件的在线预测校正制导方法。梁子璇和任章［19］采用飞行器气动参数在线修正的方法，根据再入滑翔飞行器的三自由度运动方程预测飞行器落点，通过落点偏差生成制导指令。王俊波等［20］采用飞行器平面再入段运动方程，基于模糊逻辑预测飞行器落点，生成飞行器制导指令。

根据上述讨论可以看出，现有基于落点预测的制导律均依赖于弹体/飞行器的气动参数和简化运动方程，需要通过常微分方程在线求解或运动状态估计方法预测落点。显然，用于落点预测的数学模型越精确，落点预测结果也越精确，可以提高制导律的性能，但是制导律在线计算成本将随之提高。

本文提出了一种基于落点预测的新型制导律设计方法，采用目标跟踪问题中常用的随机机动模型和自适应卡尔曼滤波器估计弹体的飞行状态，根据代数方程的解析解预测弹体落点，进而生成制导律。该制导律不依赖于弹体气动参数和运动方程，避免了在线求解常微分方程所带来的计算成本。通过数值仿真检验了所提制导律的制导性能，根据自旋火箭弹的非线性数学模型，研究了所提制导律在标称参数条件下的落点误差，检验了在参数受扰条件下的火箭弹落点散布，并与比例制导律进行制导性能对比。

1 基于落点预测的制导律设计

本文研究基于落点预测的制导律设计，采用随机机动模型和自适应卡尔曼滤波器估计弹体的平动运动状态，在不依赖于弹体气动参数和弹体运动常微分方程在线求解的条件下预测弹体落点，根据落点与目标间的偏差设计制导律。

1.1 随机机动模型

考虑图1所示的弹体和目标，为了提高弹体的精度，可以通过预测弹体落点与目标间的偏差，设计用于控制和修正弹体轨迹的制导律。对于射程较近的弹体，地球曲率和地球自转对弹体飞行的影响较小，可以采用平面地球假设，并将地面上任意一点视为惯性原点。本文采用的惯性参考系O-x1x2x3如图1所示原点选在弹体的发射点，Ox1轴指向弹体发射方向，Ox3轴垂直于地面向下，Ox2轴根据右手定则确定。

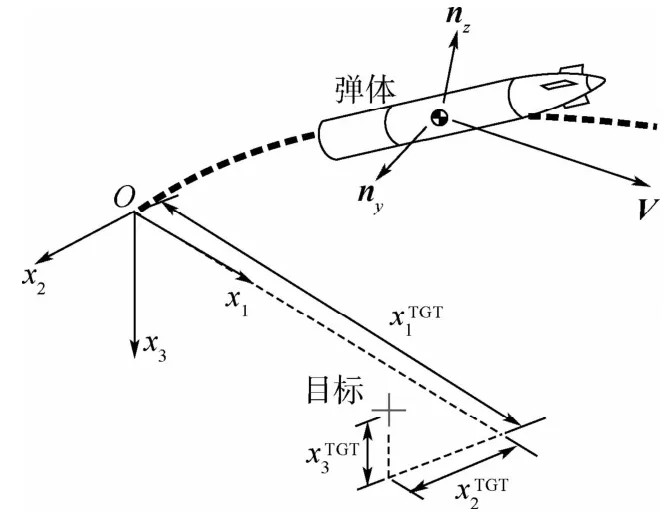
图1 参考系定义Fig.1 Definition of reference frames

由于弹体落点与弹体在参考系O-x1x2x3中的平动运动有关，本文采用“当前”随机机动模型和自适应卡尔曼滤波器估计弹体当前的平动运动状态［21］。该模型采用Rayleigh密度函数对弹体在惯性参考系Oxi轴的平动加速度ai（t）（i=1，2，3）进行建模，ai（t）的期望和方差分别为E（ai）和，弹体在Oxi轴的平动运动方程可写为

式中：αi为机动时间常数，用于衡量弹体的机动能力，一般而言，对于机动能力较高的弹体，αi可取为αi=1/20，对于机动能力较低的弹体，αi可取为αi=1/60［22］；为平均加速度，在一个采样周期内认为是常数；wi（t）为零均值且方差为的白噪声信号。

当采样周期为T，每个采样时刻仅测量弹体在Oxi轴的位置xi（t），式（1）的离散形式可表达为

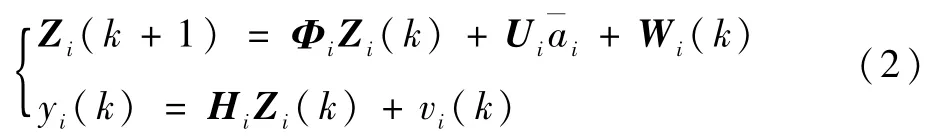
式中：vi（k）代表测量噪声，为零均值且方差为ri（k）的白噪声信号；yi（k）为测量输出；Wi（k）为激励输入［21-22］；状态变量Zi（k）和矩阵Hi分别为

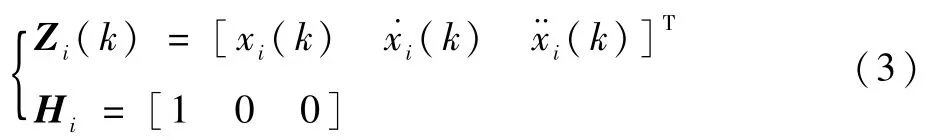
矩阵Φi和向量Ui分别定义为

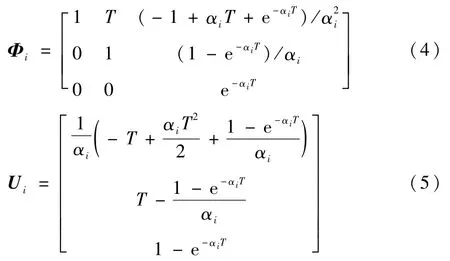
根据式（2）中的离散状态方程，可根据如下所示的自适应卡尔曼滤波器确定弹体平动运动状态的估计值。

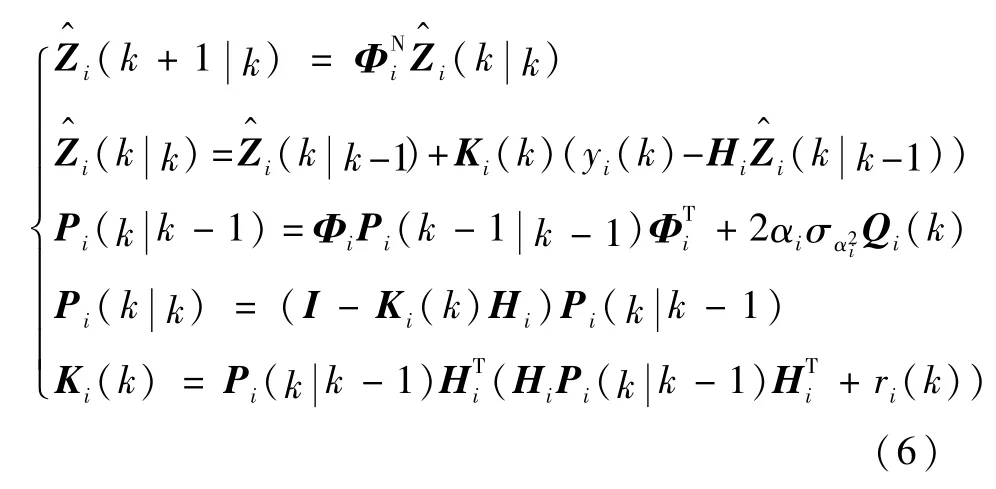
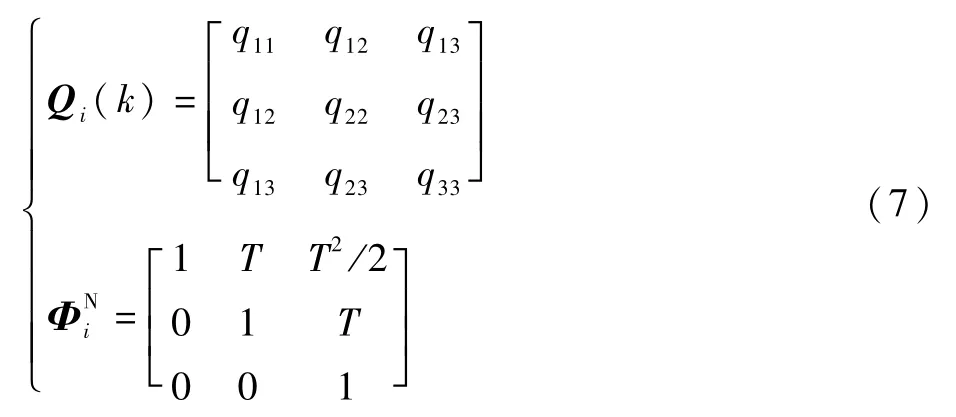
矩阵Qi（k）的每个元素可分别定义为

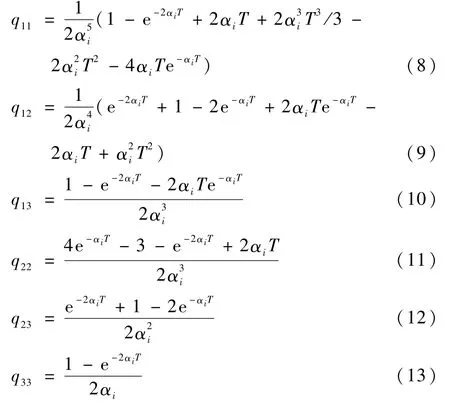
1.2 落点预测与制导律设计

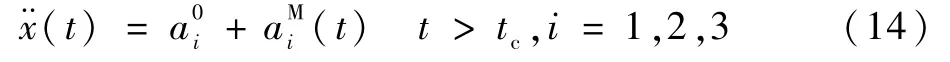
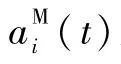
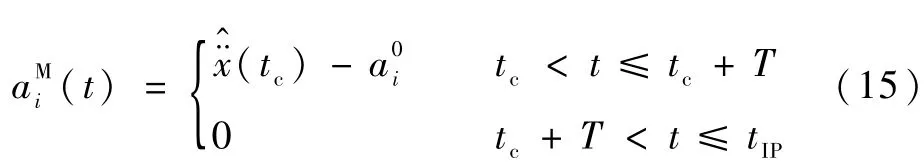
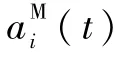
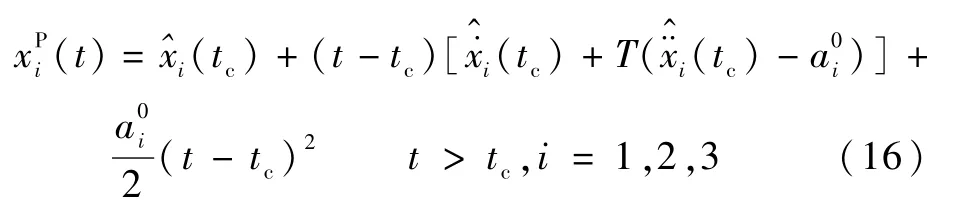
2 数值仿真

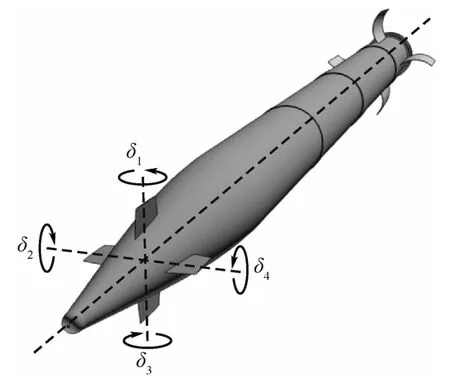
图2 火箭弹构型Fig.2 Configuration of an artillery rocket

采用自旋火箭弹的非线性数学模型，通过数值仿真检验本文所提出的制导律在标称参数条件和参数受扰条件下的制导性能。火箭弹的前端装有4个对称分布的控制舵面，每个舵面的舵偏角为δi（i=1，2，3，4），火箭弹构型和舵面偏转角正方向定义如图2所示。

控制和制导过程中，主要测量火箭弹的位置和滚转角，火箭弹的当前位置根据GPS接收器测量，火箭弹的滚转角通过磁传感器和加速度计的综合测量得到。该自旋火箭弹是动稳定的，可采用开环控制方式控制火箭弹轨迹，舵面偏转规律为

式中：φ为火箭弹滚转角；δc和δs分别为纵向和横向等效舵偏角，分别用于火箭弹法向和横向过载控制。针对该火箭弹的开环控制方式，式（17）中的制导律可改写为

表1 火箭弹仿真参数Table 1 Parameters for artillery rocket simulation

2.1 标称参数条件下的制导性能

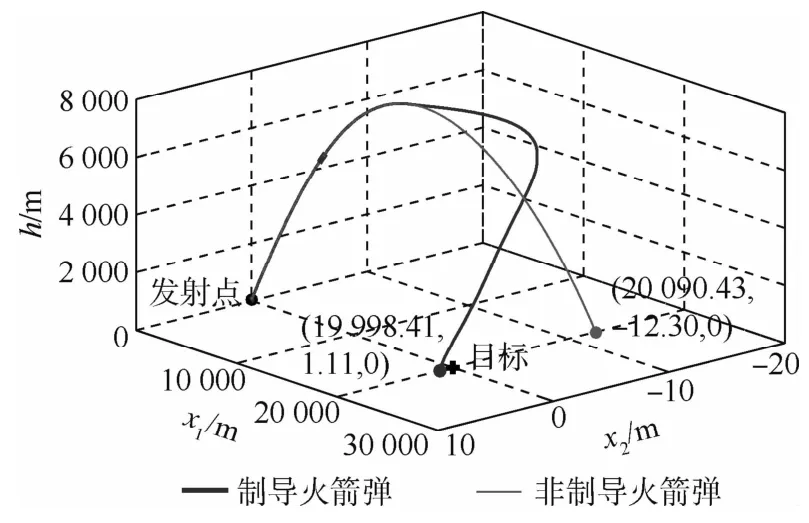
图3 制导和非制导火箭弹轨迹对比Fig.3 Trajectory comparison between guided and unguided artillery rockets

在标称参数条件下的制导火箭弹和非制导火箭弹轨迹对比结果如图3所示。可以看出，非制导火箭弹的落点明显偏离目标，而式（19）中的制导律能够显著减小制导火箭弹落点与目标之间的偏差。非制导火箭弹的落点误差为91.27m，而制导火箭弹的落点误差可降低至1.94m。显然，本文提出的制导律在标称参数条件下具有良好的制导性能。

图4为火箭弹纵向和横向等效舵偏角。可以看出，纵向等效舵偏角δc在制导阶段的初期存在相对较大的偏转，但最大舵偏角未超过25°；在制导阶段末期，δc的偏转较小，最大舵偏角小于10°。产生该现象的原因在于制导阶段初期火箭弹距落点较远，随机机动模型给出的落点估计值的精度较低，制导律将给出相对较大的舵偏角以修正火箭弹轨迹。

图4中的横向等效舵偏角δs在制导阶段呈现先增后降的变化趋势。产生该现象的原因在于制导律是在火箭弹在达到弹道最高点后开始工作的，在弹道最高点处弹体与目标之间已存在较为明显的横向偏差（见图3所示的火箭弹轨迹）。因此，在制导阶段的初期，随机机动模型给出的预测落点与目标之间也会出现较大的横向偏差，导致δs的偏转增大，用以修正火箭弹轨迹。随着制导律的持续工作，火箭弹轨迹与目标之间的横向偏差逐步减小，所以δs偏转也随之减小。总体而言，δs的偏转较小，最大舵偏角未超过1°。显然，式（19）中制导律所生成的舵偏角指令是合理的，能够避免制导过程中火箭弹舵面的大幅偏转。

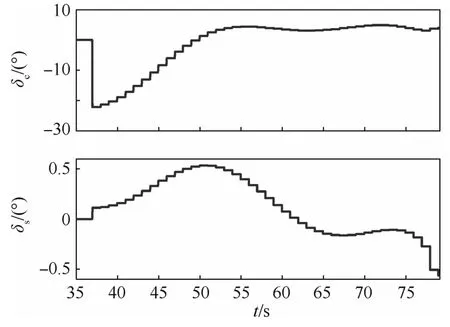
图4 制导火箭弹等效舵偏角Fig.4 Equivalent canard deflections of guided artillery rocket

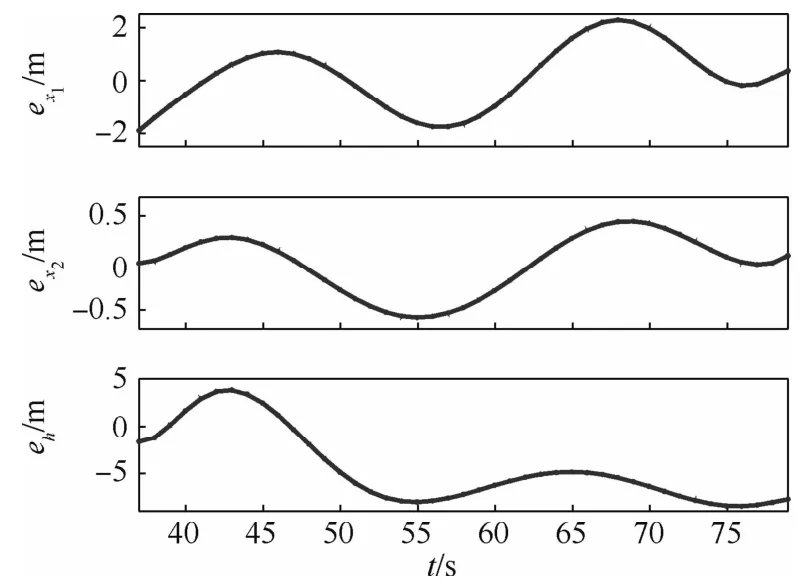
图5 制导火箭弹位置的估计误差Fig.5 Estimation errors of guided artillery rocket locations

图5为随机机动模型和自适应卡尔曼滤波器给出的火箭弹位置估计误差。可以看出，火箭弹在Ox1轴位置的估计误差ex1和高度的估计误差eh较小，分别在±2 m和±5 m 以内。火箭弹在Ox2轴位置的估计值较为准确，估计误差ex2在±0.5m以内。这些估计误差是可接受的，对制导火箭弹落点预测和制导性能的影响较小。

2.2 参数受扰条件下的制导性能

为了检验本文提出的制导律在参数受扰条件下的制导性能，分别对制导火箭弹和非制导火箭弹进行100次Monte Carlo仿真，对比落点分布和相对于目标的圆概率偏差（CEP）。对于每个受扰的参数，扰动误差服从均值为零的正态分布，即对于参数v，扰动误差为Δv且Δv～N（0，σ），其中σ为均方差。Monte Carlo仿真的初始参数标称值采用表1中所示的参数，仿真所采用的受扰参数和对应的均方差如表2所示。

落点分布结果如图6所示，图中Δx1和Δx2分别为火箭弹在Ox1轴和Ox2轴的落点误差。非制导火箭弹的CEP为219.05 m，制导火箭弹的CEP可降低至8.91m。同时，式（19）中的制导律使得制导火箭弹的落点更加密集，绝大多数落点集中在边长为40m的正方形区域内。显而易见，本文提出的制导律在参数受扰的条件下具有良好的制导性能，能够明显提高制导火箭弹的命中精度。

表2 受扰参数的误差Table 2 Errors of perturbed parameters

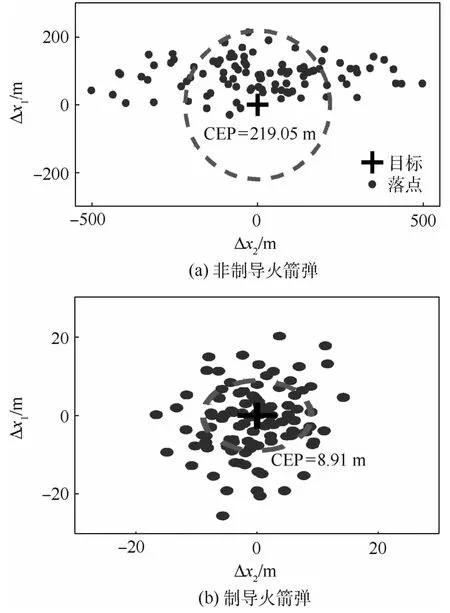
图6 制导火箭弹和非制导火箭弹落点分布Fig.6 Impact point distributions of guided and unguided artillery rockets

2.3 与比例制导律的性能对比

本节将式（19）中的落点预测制导律的制导性能与典型的比例制导律的制导性能进行对比。针对图2所示的自旋火箭弹，比例制导律可表达为

落点误差的对比结果如图7所示。可以看出，在绝大多数情况下，本文提出的制导律给出的落点误差小于式（20）中的比例制导律给出的落点误差。落点预测制导律给出的最小落点误差为0.76m，小于比例制导律给出的最小落点误差3.69m。

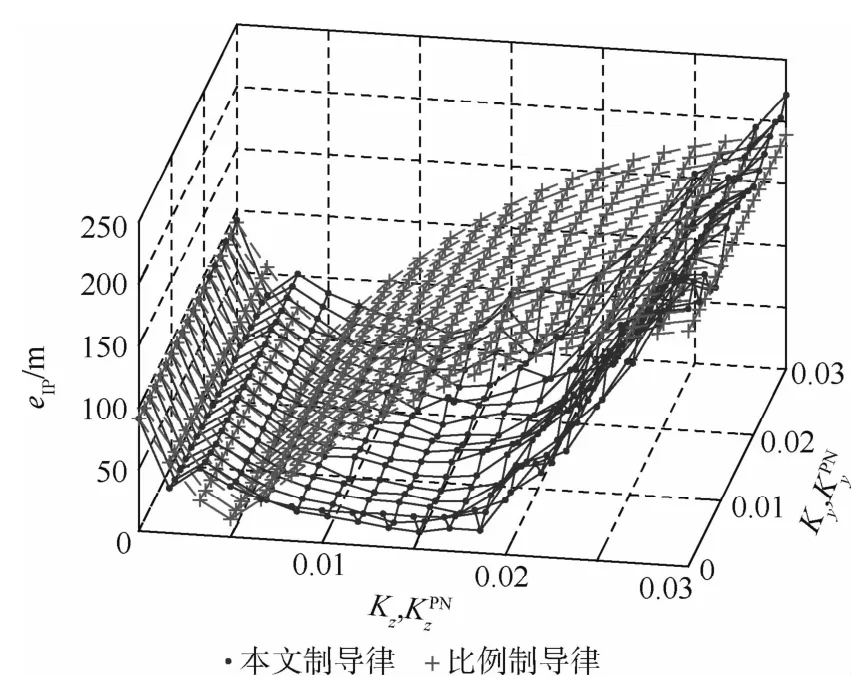
图7 本文制导律与比例制导律的性能对比Fig.7 Performance comparison between proposed guidance law and proportional navigation guidance law

3 结 论

本文提出了一种基于落点预测的新型制导律设计方法，该方法以随机机动模型和自适应卡尔曼滤波器为基础，估计弹体在各个时刻的位置、速度、加速度，采用弹体预测轨迹的解析解得到落点预测值。具体结论如下：

1）针对20 km处的目标，在标称参数条件下的数值仿真中，该制导律可将火箭弹落点误差从91.27m降低至1.94m。

2）针对20 km处的目标，在参数受扰条件下的数值仿真中，制导火箭弹的CEP为8.91m，远低于非制导火箭弹的CEP，即219.05m。

3）与比例制导律的性能对比中，该制导律的最小落点误差小于比例制导律的最小落点误差。

4）该制导律不依赖于弹体气动参数，无需在线进行弹体运动方程的数值求解，可用于低成本制导武器的制导律设计。