基于多约束因子图优化的无人车定位与建图方法
牛国臣,王瑜
(中国民航大学 机器人研究所,天津300300)
无人车沿着特定路线行驶,实现如机场摆渡车、观光车,在工厂或封闭园区巡逻、货物搬运[1]、卫生清扫以及安保监测[2]等功能,已经成为未来的发展趋势。定位问题是无人驾驶中的关键问题[3]。最常见的定位方法是基于全球导航卫星系统(Global Navigation Satellite System,GNSS),其中全球定位系统(Global Positioning System,GPS)创立时间较早,应用最为广泛,使用基于载波相位的差分GPS技术RTK定位精度可达到分米级[4]。但是在实际应用中,树木、楼房建筑物等高大物体的遮挡均会对GPS信号的强度产生影响,导致定位失效。为了克服信号不足的问题,常用卡尔曼滤波器将GPS与惯性导航系统(Inertial Navigation System,INS)耦合[5-6],但是高精度惯性导航元件较为昂贵,且存在累积误差。近年来结合高精度地图(High Definition Map,HD Map)[7]的 无 人 车 匹 配 定 位 发 展 较 为 迅 速[8],但HD Map的构建需要昂贵的测绘系统和人工标注等复杂的后处理步骤[9],成本十分昂贵,不适用于特定场景下无人车的大规模应用,构建一个低成本、可靠且在复杂环境下鲁棒的定位与建图系统已成为无人车产业级应用的需求。
为了解决上述问题,机器人导航领域的关键技术之一,同时定位与建图(Simultaneous Localization and Mapping,SLAM)技术被用于解决无人驾驶的定位问题[10-11]。其中,基于激光雷达的三维激光定位与建图(SLAM)方法不受光照影响,数据量相对较少,创建的地图精度更高,在无人车中应用更为广泛。Zhang和Singh[12]提出了一种基于激光雷达的实时定位和地图(LiDAR Odometry and Mapping,LOAM)构建方法,该方法通过激光雷达来获取点云图,并使用非线性最小二乘优化方法来优化角点和平面点的距离,同步实现了高频率的里程计和低频率的建图,实时性较好,但由于缺少后端优化,累积误差导致所建点云地图欠准 确,全 局 一 致 性 低。Shan和 Englot[13]在LOAM框架基础上,提出了改进方案Lego-LOAM,使用迭代最近点(Iterative Closest Point,ICP)算法实现了闭环检测和全局优化的建图功能,利用高层次几何特征提高了空间结构的描述效率,但该方法所建地图为较稀疏的特征点地图,难以用于定位。Ji等[14]提出了一种改进LOAM 方案,在LOAM的框架中加入了GPS约束,该方法在局部估计中获得了较高的准确性,GPS先验信息可消除部分激光里程计带来的累积误差,但点云地图的“重影”问题明显。Deschaud[15]提出了一种扫描到模型(Scan to Model)的匹配方法,通过最小化当前点到以隐式移动最小二乘(Implicit Moving Least Squares,IMLS)表示的表面之间的距离来完成位姿估计,实现了稳定准确的点云匹配,但计算量大,难以用于实际系统。Chen等[16]提出了一种基于语义特征的改进LOAM 方案,用于森林中树木模型的检测,但该方法仅对环境中树木的语义特征进行提取,对于无人车应用场景来说,单一的环境特征远远不够,并且还需要考虑大规模点云语义分割带来的计算量问题。
综上,以LOAM为首的激光里程计作为应用程度最为广泛的激光SLAM 主流方案,仍存在大规模场景中无法消除累积误差、所建的点云地图无法用于定位的问题。而Lego-LOAM 等增加了闭环约束的改进方案,使系统增加对历史观测信息的判断、保存和校正,提高轨迹的全局一致性,构建较精确的全局地图,提高地图精度。增加了GNSS以及地平面等先验环境信息的方案,为SLAM 系统后端增添约束,可显著优化激光里程计的误差,提高姿态精度。在实际应用中,无论是姿态精度还是地图精度均会影响无人车的定位效果。目前虽然有一些研究提出了较为完整的SLAM方案,但都处于研究阶段,未考虑无人车的实际应用场景。
基于此,本文设计了一个低成本、高精度的无人车定位与建图系统,为满足实时性,提出一种基于主成分分析(PCA)算法进行点云特征提取与匹配的激光里程计。针对点云地图的“重影”和激光里程计的累积误差问题,从因子图优化角度构建了一个完整的三维激光SLAM 系统,将GNSS(以GPS为例)及地平面等先验信息和基于聚类特征的闭环检测使用图优化框架融合到SLAM系统中,并使用KITTI数据集测试了该系统的性能。
1 系统概述
本文所提出的算法框架如图1所示。首先,对点云数据进行运动补偿、体素滤波和分割等预处理操作;其次,在前端实现一个基于特征匹配的激光里程计,将地平面约束、GPS约束作为一元边,聚类特征作为闭环约束加入到图中,在后端进行位姿图优化,得到最优位姿,增量显示轨迹并存储相应帧的点云数据构建点云地图。

图1 系统整体结构Fig.1 Overall structure of system
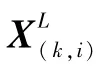
2)IMU坐标系I,以IMU重心为坐标原点,分别沿IMU水平轴和纵向轴设置X轴和Y轴,Z轴垂直于XY平面。
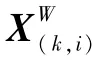
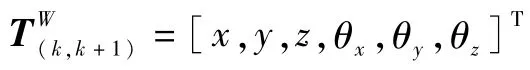
2 SLAM 方案
在本节中将介绍激光SLAM 系统的各个子模块,包括点云预处理、激光里程计、多约束因子图和图优化等4个模块,并对其理论内容进行推导。
2.1 点云预处理
根据LiDAR的扫描方法,按空间和时间顺序记录这些点以进行遍历。由于在LiDAR的扫描过程中,车辆已经移动,为此引入IMU 位姿信息[12]对LiDAR运动进行补偿,得到去除点云畸变的当前帧。激光点云信息量巨大,在进行帧间匹配之前,将输入点云S经过体素滤波去除噪点和地面点,对剩下的点云进行欧氏聚类,滤除动态物体等无效点。
本文提出一种轻量级地平面分割方法。设定无人车前进的方向为世界坐标系X轴的正方向,将点云的三维空间XYZ降到二维平面XY,根据激光雷达投影到地面的射线中前后两点的坡度是否大于事先设定的坡度阈值来判断点是否为地面点。
激光雷达安装在车辆顶部并与地面平行,雷达由下至上分布多个激光器,发出一系列放射状激光束,这些激光束在平地上即表现为一条射线,如图2所示。

图2 地平面分割方法示意Fig.2 Schematic diagram of ground plane segmentation method
因雷达安装高度固定,对于平坦的地面,可以根据LiDAR返回的坐标值得到点到LiDAR的距离,对于任一点i,i∈S有

式中:xi和yi为i点在LiDAR坐标系L下的坐标位置;θi为点相对于车头正方向(X方向)的夹角;ri为i点到LiDAR的水平距离。
将同一射线上的点按照水平距离ri排序,计算同一条射线上相邻两点的坡度。

式中:zi为i点的垂直高度;ai,i+1为i点和i+1点之间的坡度;h为LiDAR的安装高度。
为了避免地面不平或是LiDAR并未完全平行于地面安装等微小因素引起的检测误差,定义一个阈值threguler,将式(2)结果与此阈值作比较,当ai,i+1<threguler即将i点归为地面点。
对去除地面点后的点云进行欧氏聚类,为了达到更好的聚类效果,在以LiDAR为圆心的不同距离区域内使用不同的聚类半径阈值,效果如图3所示。

图3 点云预处理效果Fig.3 Point cloud pretreatment effect
场景中的运动物体严重影响建图过程的准确性,但是从扫描中删除所有动态对象,需要场景的高水平语义信息,对点云进行语义分割耗时较长,不适用于实时系统。本文通过删除小型物体来替代动态物体删除,从场景中丢弃那些尺寸被认为可能是动态物体的对象。将可能是行人、汽车、公交车或者货车等小的点类去除,移除聚类边界框X方向上小于10m,Y方向上小于5 m,Z方向上小于4m的点类,保留足够的大型基础设施信息,如墙壁、栅栏、立面和树木(高度超过4 m),确保激光雷达里程计特征匹配过程中角点和边缘等特征信息足够。
2.2 激光里程计
LOAM根据激光雷达的特性,按照扫描线的空间顺序和时间顺序提取特征点。在本文中对其简化,引入主成分分析计算点云主方向,以满足计算的实时性和准确性要求。当前帧点云表示为

式中:xi、yi和zi,i∈(1,2,…,n)为经过点云坐标系到世界坐标系的坐标转换后的点云坐标。
将点云分别投影到X轴、Y轴和Z轴上,计算协方差矩阵为

式中:cov为协方差算子,对每个点分别计算其x坐标、y坐标以及z坐标之间的协方差。例如,cov(x,y)为x坐 标 与y坐 标 之 间 的 方 差,当cov(x,y)>0时,x和y正相关,cov(x,y)=0时,x和y相互独立。协方差由式(5)计算:

式中:xi和yi为点云坐标;n为当前帧点云中点的个数。
计算协方差矩阵C的特征值和特征向量,根据特征值将特征向量从大到小排列,组成特征矩阵U。
设点i为在tk处获得的特征矩阵Uk中的点,R点为i周围10个连续点的集合,通过围绕点i的10个矢量之和的范数的大小来评估点i附近局部表面的光滑度。定义光滑度c为
根据点的时间戳将Uk分为4个部分,并根据光滑度c的值对每个部分进行排序,选择值最大的2个点作为拐角点,值最小的4个点为平面点。
在进行帧间匹配时,同一帧内的2个连续角点可以形成一条边缘线,3个平面点可以形成一个平面。利用帧间变换矩阵T将k+1帧的点变换回第k帧,则属于k+1帧的角点和平面点分别到属于k帧的边缘线以及平面的距离应该为0,设该距离的向量形式为d,T的初值可由IMU提供的车辆位姿得到。求d的最优值即是一个典型的非线性最小二乘问题。使用Levenberg-Marquardt(L-M)优化方法最小化d,得到最优的T:
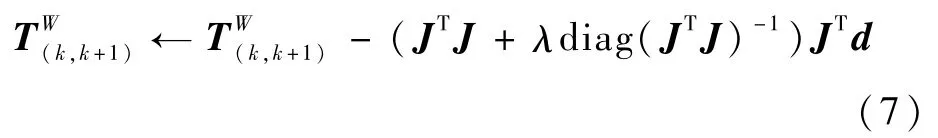
2.3 多约束因子图
因子图由“顶点”和“边”组成[17],具体到SLAM问题中,“顶点”为车辆的位姿,“边”为位姿之间的约束[18]。为了解决长距离漂移问题,本文提出设有一种包含地平面约束、GPS约束、点云聚类特征闭环约束和前端里程计约束的多约束因子图,如图4所示。图中:Gi为由GPS数据生成的固定节点;Ti为三维位姿变换SE(3)中的车辆位姿节点;π0为地平面节点。
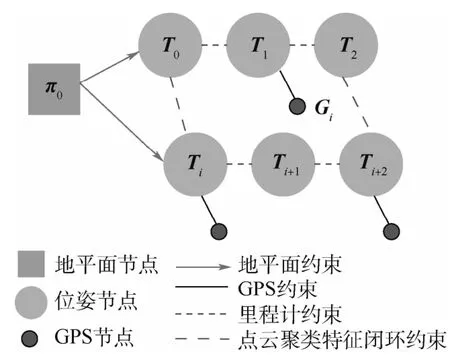
图4 因子图结构Fig.4 Structure of factor graph
2.3.1 地平面约束
在2.1节点云预处理中已完成地平面的检测,将地面局部建模为π=[nx,ny,nz,a]T参数化的平面[19],nx、ny和nz为平面的法线,a为原点到平面的距离,对于平面上的任一点xi、yi、zi,有xinx+yiny+xinz+a=0。
为了计算车辆姿态和地平面之间的误差,需要将车辆的姿态节点与固定的地平面节点相连,先进行坐标转换,用初始时刻的地平面和车辆姿态,得到由车辆姿态估计的地平面,即


采用最小参数法定义平面参数表达式为

式中:arctan(ny/nx)为平面方位角;arctan(nz/n)为平面仰角;a为截距,表示原点到该平面的距离。则位姿节点和地平面节点之间的误差被定义为

式中:πt为t时刻检测到的地平面。
2.3.2 GPS约束
为了便于优化,首先将GPS数据转换为UTM坐标,然后将每个GPS数据与位姿节点相关联[20],位姿节点与GPS数据的时间戳对齐,则GPS位置即可作为先验位置信息,成为位姿节点的一元边缘。位姿节点的平移矢量与GPS位置之间的误差定义为

式中:Tt为t时刻的车辆位姿;Gi为GPS数据生成的固定节点。
2.3.3 点云聚类特征闭环约束
在2.1节中已得到一系列点云聚类,分别进行几何特征和直方图特征提取,用于随后的标识和分类[21-22]。提取的点云段特征由特征向量f=[f1f2… fn]表示,每个元素代表局部或全局描述方法。通过计算点云段中的点与其质心之间的差,可以获得点云段的3D结构张量及其特征值λ1、λ2和λ3。参照SegMatch方法[23]计算点云的线性度(Lλ)、平面度(Pλ)、散射度(Sλ)、全方差(Aλ)、各向异性(Oλ)、特征熵(Eλ)和曲率变化度(Cλ),特征描述符如下

式中:zi为归一化的特征值。
直方图特征包含随机两点的距离统计、随机三点组成的三角形面积统计以及随机三点组成的一个角的角度统计等3种。
在完成聚类特征提取后,先基于点云聚类闭环匹配得到当前帧与地图的粗匹配,再采用扫描到地图(Scan to Map)模型[24],以当前时刻点云帧为中心,按照时间向前和向后各索引数帧点云组成局部地图,利用正态分布变换(Normal Distribution Transform,NDT)得到当前点云和局部地图间的精确变换。
为了提高闭环检测的效率,避免频繁检测造成计算量过大问题,设置闭环检测帧的最小时间差,滤除时间间隔较近的匹配。最终将闭环得到的变换矩阵,作为位姿约束输入后端进行优化。
2.4 图优化
本文采用g2o优化库,对最终建立的位姿图进行优化[25]。当优化了整个LiDAR运动的位姿图后,将位姿节点对应的三维点云帧进行拼接,从而得到全局一致的轨迹和地图。
3 实验分析
为了验证本文方法的可行性,选择无人驾驶数据集进行实验。目前KITTI数据集是评估SLAM 的最受欢迎的数据集,为本文的实验评估提供了真实的数据。实验借助Linux下的机器人操作系统(Robot Operating System,ROS)架构,在具有2.20 GHz×4的i5-5200 CPU和12 GB内存的计算机上运行。
3.1 定位精度
以KITTI数据集提供的真值作为参考,将SLAM 轨迹与真值进行对比,通过计算位姿轨迹与真实轨迹之间的相对位姿误差(Relative Pose Error,RPE)和绝对轨迹误差(Absolute Trajectory Error,ATE)来评估本文方法的定位精度。
3.1.1 准确性分析
RPE是指在固定长度的间隔内,估算位姿和真实位姿之间的差值,相当于直接测量激光里程计的误差。为了体现本系统的定位效果,以KITTI数据集作为输入数据,采用经典的LOAM 方法和本文方法,分别在短距离运动场景(1 392m)和长距离运动场景(3 714m)2种模式下进行实验,将里程计数据存储并解算,每隔50 m 统计一次RPE,以此评价姿态精度。表1中列出了不同运动场景的数据帧数、轨迹长度以及RPE的详细值,包括最大值、平均值、中值以及均方根值(Root Mean Square Error,RMSE)等。

表1 相对位姿误差对比Table 1 Comparison of Relative Pose Errors(RPE)
可以看到,无论是在短距离还是长距离运动环境下,本文方法的RPE要明显低于LOAM 方法,经典的LOAM 方法在短距离运动场景下RMSE为0.39m,但是在长距离运动环境下,里程计精度降低,而本文方法在长距离实验测试中,RPE的RMSE值可保持在1.5m以下,适用于无人车的应用场景。图5为本文方法和LOAM方法在长距离运动环境下,RPE值和点云序列之间的关系,为了对比更为明显,LOAM 方法用虚线表示,本文方法用实线表示。
通过比较可以看出,本文方法对应的曲线更加缓和,相对来说跳变较少,虽然在第12次计算时出现了较大误差值,但系统的图约束消除了部分漂移,随后误差变化逐渐趋于平稳。与本文方法相比,随着车辆运动距离的增加,LOAM 方法的累积误差逐渐增加,曲线增幅逐渐变大,这可说明本文方法在无人车较长距离运动环境中的可靠性更高、稳定性更好。
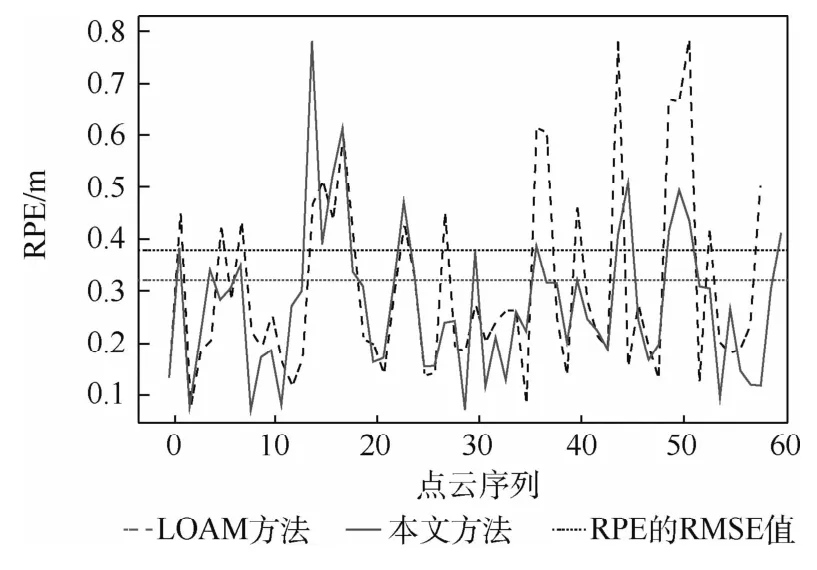
图5 相对位姿误差和点云序列曲线Fig.5 Curves of RPE and point cloud sequence
3.1.2 一致性分析
对于SLAM系统一致性的评估,本文引入绝对轨迹误差(ATE)指标,根据时间戳对齐位姿的真实值和SLAM系统的估计值,计算每对位姿之间的差值,最后对ATE进行评价。这里同时考虑旋转和平移带来的影响。表2中列出了ATE的详细值,包括最大值、平均值、中值以及RMSE等。
图6为使用本文方法和LOAM 方法得到的ATE值和点云序列之间的关系。LOAM 没有GPS、地平面以及点云聚类特征等约束信息,虽然在开始时轨迹误差可维持在10 m以下,但在运行一段时间后,因为累积误差,位姿发生偏移,并且这种偏移随着车辆运动轨迹的增长而递增;本文方法由于加入了先验和闭环等信息,使得车辆在运动过程中时时修正位姿的偏移量,从而可以保证车辆运动轨迹更贴近真实轨迹。

表2 绝对轨迹误差对比Table 2 Comparison of Absolute Trajectory Errors(ATE)
图7为使用本文方法得到的车辆运动轨迹与参考轨迹的对比,其中SLAM 系统的估计位姿越靠近真实位姿即表示误差越小。从表1中已知使用经典的LOAM 方法只适合于车辆运动距离较小时,随着运动时间增长,里程计带来的漂移误差随着LiDAR的运动逐渐增加,使位姿严重偏离真实轨迹。与LOAM相比,本文方法所得到的轨迹与真实轨迹基本一致,全局一致性高,可以进一步提高无人车定位与建图的精度。
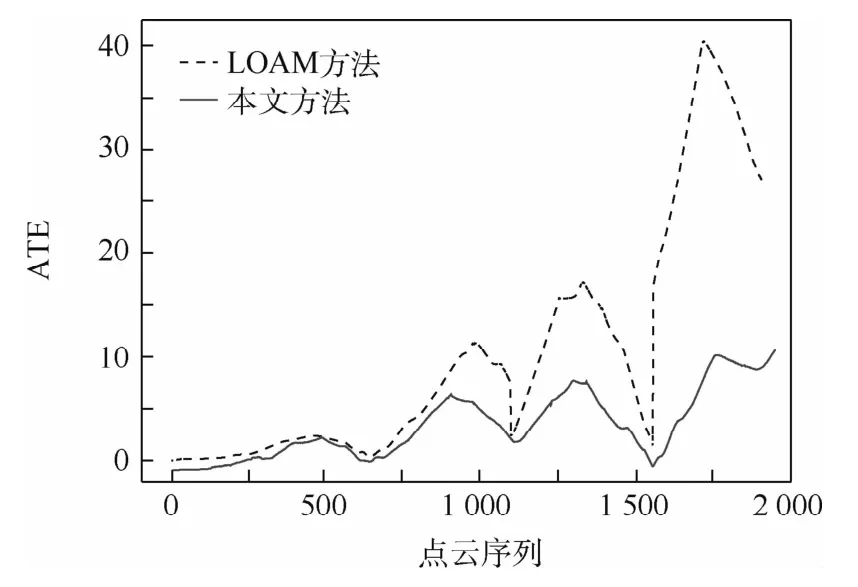
图6 绝对轨迹误差和点云序列的变化曲线Fig.6 Change curves of ATE and point cloud sequence

图7 SLAM系统得到的轨迹与参考轨迹对比Fig.7 Comparison between trajectory obtained by SLAM system and reference trajectory
3.2 建图效果
为了验证本文方法的大规模建图效果,将通过SLAM方法得到一系列连续位姿形成的位姿轨迹对应的点云帧转换为世界坐标系,拼接生成点云地图,如图8所示,基于点云的三维地图可用于后期无人车定位。
在实验中,图8(a)、(b)分别为使用LOAM方法和本文方法得到的建图场景俯视图,图中A、B、C均为点云地图局部细节效果。可以看到,由于缺乏闭环检测和后端图优化,图8(a)中地图出现了较多的重影和模糊的现象,如图中框选中区域所示,点云帧之间误差较大,漂移严重甚至导致地图构建失败,在框选中C部分,点云帧间匹配丢失,所建地图未闭合。本文方法所建地图与真实环境基本吻合,图8(b)中地图封闭且完整,边界清晰,无明显重影,效果较好。

图8 点云地图Fig.8 A point cloud map
4 结 论
本文提出一种基于多约束因子图优化的三维激光SLAM方案,经实验验证可得到以下结论:
1)基于PCA算法和点云特征匹配的激光里程计可以有效应对无人车室外环境定位,该匹配方法简单且鲁棒,实时性好。
2)加入地平面、GPS数据等先验信息以及点云聚类特征闭环约束的多约束因子图,降低了前端里程计的累积误差,解决了构建地图时的重影问题,同时提高了定位精度。
3)以三维激光SLAM 的代表性方法LOAM与本文方法进行对比验证,实验证明,本文方法在长距离实验测试中,RPE可达到1.5 m以下,适用于无人车的应用场景。
下一步计划将此系统用到无人车实际系统中,探索复杂环境下高精度的无人车定位与建图方法。

