利用正交位移测量系统进行六自由度并联机构参数标定
杨利伟,鲍 赫,樊延超,李志来,董得义
(中国科学院长春光学精密机械与物理研究所,吉林长春130033)
1 引 言
六自由度并联机构因其具有高精度、高刚度、无累积误差等优点,被广泛用于光学元件精调、超精密加工等领域[1]。
由于加工及装配误差的存在,六自由度并联机构的实际结构参数与理论结构参数存在一定偏差,这将导致运动学模型不准确。由于结构参数偏差的存在,六自由度并联机构按照指令进行运动时,实际位姿与模型理论位姿会存在一定偏差。采用高精度机床对并联机构的结构件进行加工,可降低结构件加工误差,但成本高昂,而通过参数标定对误差进行补偿,是一种低成本且行之有效的方法[2-3]。
通常并联机构的标定包括误差建模、位姿测量及参数辨识三个步骤。其中,并联机构末端执行器位姿测量是标定的关键环节。标定过程中,根据测量输出不同可以将标定分为两类:自标定法和外部标定法[4]。自标定法不需要外部测量设备,利用源于运动平台自身的冗余信息来辨识其几何参数,该方法在标定过程中不但需要求解标定模型的正解,而且无法获得末端位姿的全部信息,因此精度提高受到一定限制;外标定法也称开环标定,通过外部测量工具获取运动平台的位姿信息,据此来辨识平台的几何参数。目前针对并联机构的标定,仍以外部标定方法为主。常用的外部测量装置包括三坐标测量机[4]、测量臂[5]、激光跟踪仪[6]等设备,这些设备虽具有精度高、适应性广等特点,但造价昂贵,而且在应用时存在两个方面的问题:一是测量前需要对测量仪器进行精细调整,耗时较长,导致标定效率较低;二是部分测量仪器(如三坐标测量机)对操作人员、操作环境要求较高,应用不便。综合上述原因,上述位姿测量解决方案有待进一步改进。
本文针对六自由度并联机构的位姿测量过程中存在的问题,提供一种简洁高效的六自由度并联机构参数标定装置及方法,达到降低成本、简化标定过程、提升标定效率的目的,对今后的并联机构的参数标定具有重要的指导意义。
2 正交位移测量系统正逆解分析
2.1 正交位移测量系统构成
传统的位姿测量方法操作简单,适用范围广,但由于基准点坐标无法直接测量得到,需要采样多个点拟合得到,导致数据量需求较大,标定效率较低。以最简单的球面拟合为例,至少需要采样4个点才能拟合出一个基准点的坐标,而解算位姿至少需要3个点,即针对每个名义位姿,至少需要测量12个点,才能解算出其对应的实际位姿,这种做法显然是耗时耗力的。
受激光六维测量系统的启发[7-8],拟构造接触式正交位移测量系统(以下简称正交位移测量系统),来开展并联机构动平台的位姿测量与解算。正交位移测量系统简图如图1所示,主要包括被测基准块、位移传感器等,其中被测基准块固定在动平台上,在被测基准块三个正交方向密布若干位移传感器,位移传感器固定在传感器座上,传感器座与定平台无相对运动;位移传感器的触头在弹力的作用下,始终与被测基准块保持接触。工作原理如下:动平台按照控制器指令进行六维运动,被测基准块随之运动,位移传感器随之做一维伸缩运动,记录位移传感器示值,通过某种解算方法,解算出动平台相对于定平台的位姿。
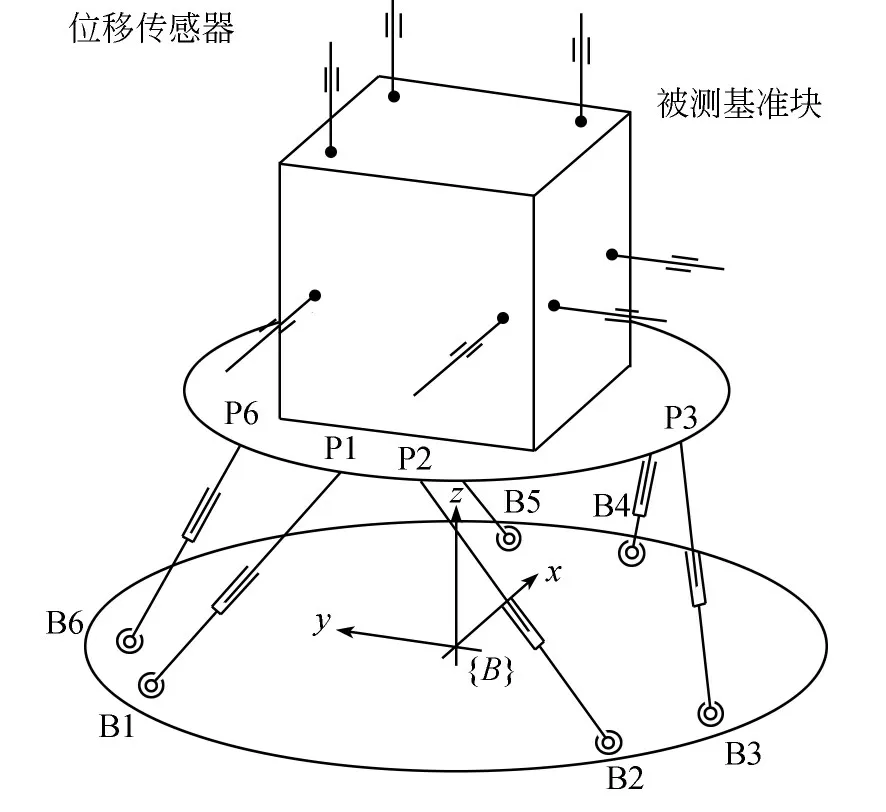
图1 正交位移测量系统简图Fig.1 Diagram of orthogonal displacement measurement system
由图1可知,正交位移测量系统可以看做是一套机构,主动件为并联机构末端执行器,从动件为位移传感器,执行器的六维运动产生位移传感器的一维直线运动,对末端执行器位姿求解的过程即为对正交位移测量系统的运动学分析的过程。
与并联机构一样,正交位移测量系统的运行学分析同样有两个基本问题,即正解、逆解问题,由执行器的六维运动求位移传感器的一维直线运动,称为运动学正解,由位移传感器的一维直线运动求执行器的六维运动,称为运动学逆解。
由六点定位原理[9]可知,要通过运动学逆解求解执行器的六维运动,需要在被测基准块周围布置6个位移传感器,六位移传感器的布置方式有两种:321型和222型。321型正交位移测量系统的位移传感器配置为:在其中一个方向,布置3个位移传感器,在第二个方向布置2个,第三个方向布置1个;222型正交位移测量系统则是在3个正交的3个方向各布置两个位移传感器。
2.2 位姿解算方法
FAN等人[10]在利用激光干涉仪进行线性位移台的六维参数同时测量时,位姿解算方法比较简单:线位移取平均值,角位移利用三角函数求解。但是如果激光束与线性位移台的被测未能精确对准,这种解算方法容易引入对准误差,例如被测棱镜轴线与激光束轴线不一致,会产生阿贝误差,被测棱镜的横滚角与激光束的横滚角不一致,会产生横滚角误差等。
采用三坐标对被测基准块、位移传感器的空间位置进行测量,可以分别得到测量坐标系下被测基准块各平面的表达式及位移传感器的直线表达式,就可以采用空间解析几何的方法解算出被测基准块,进而解算出动平台的位姿。综上,拟采用空间解析几何的方法来求解。
222型运动学逆解涉及多元二次方程组的求解,求解过程复杂,而321型的运动学逆解较为简单,这里以321型正交位移测量系统为例,讨论运动学正逆解求解过程。
2.3 运动学正解
为便于描述微调机构定系与动系之间的关系,构建基准块坐标系{E}(以下简称基准块系),坐标原点位于三基准面交点,坐标轴与动系平行;这样在图2中,存在以下坐标系:并联机构定系{B},并联机构动系{P},基准块系{E}。
他们之间的位姿关系用相应的齐次变换矩阵来描述:

为了直观地描述上述坐标变换,可以将上述的位姿关系表示成空间尺寸链的形式[11],如图2所示。
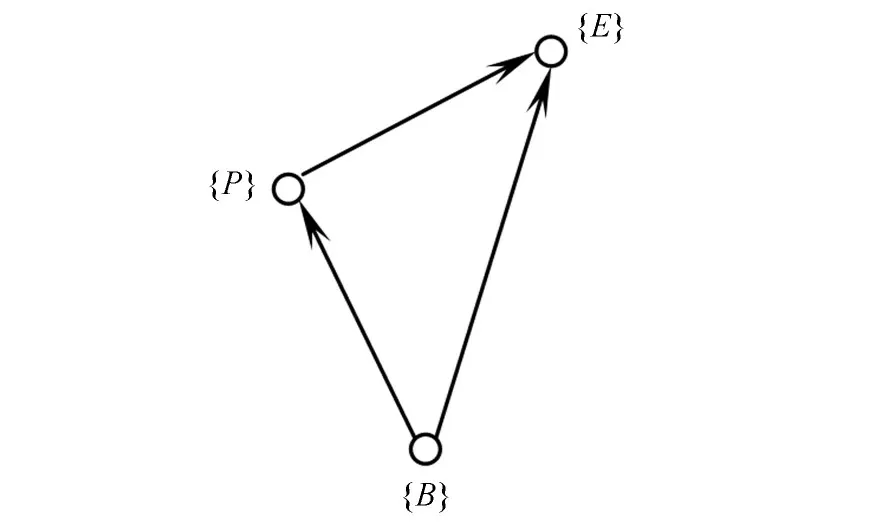
图2 空间尺寸链Fig.2 Spatial dimension chain
存在如下坐标变换方程:

假定{E}在动系{P}中的位姿为:
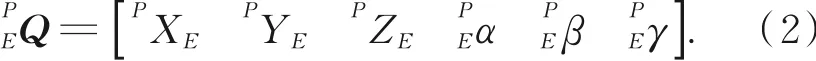
写成齐次坐标变换矩阵的形式[11],简写为:
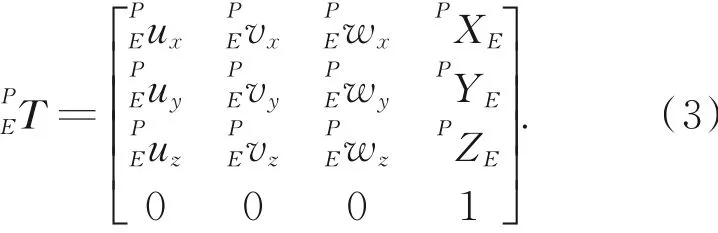
假定零位时{E}在{B}的实际位姿为:
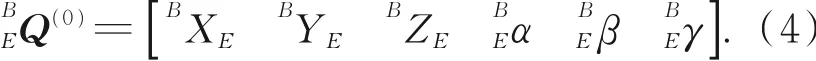
写成齐次坐标变换矩阵的形式,简写为:
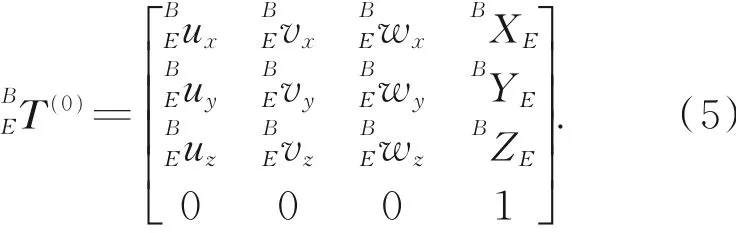
将坐标系{E}的XOY面记为Ⅰ面,XOZ面记为Ⅱ面,YOZ面记为Ⅲ面。可得平面Ⅰ的点法式方程,即[12]:
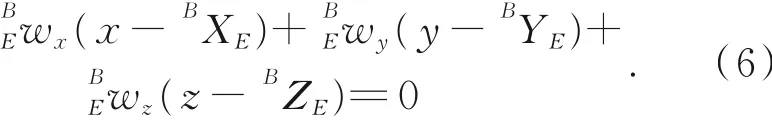
该表达式不利于编程计算。为便于编程,本文将平面Ⅰ表达式记为:
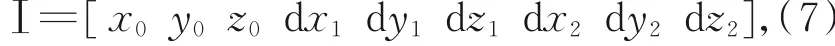
其中:P=[x0y0z0]表示平面上一点的坐标,分别表示平面内的向量,平面法向量n的指向遵守右手定则。
平面Ⅱ与Ⅲ的表达式与Ⅰ相同。
利用三坐标测量机在传感器或相应基准圆柱销上取点,拟合定系下位移传感器所在空间直线方程,拟合采用最小二乘法,这里不详细介绍。
空间直线的参数方程表达式为[12]:

该表达式也不利于编程计算,本文将过位移传感器Sk的空间直线表达式记为:
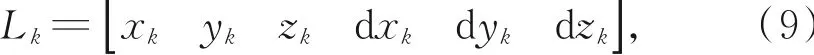
位移传感器直线方程与平面方程联立,可求出零位时各传感器与各坐标平面的触点坐标,记做:
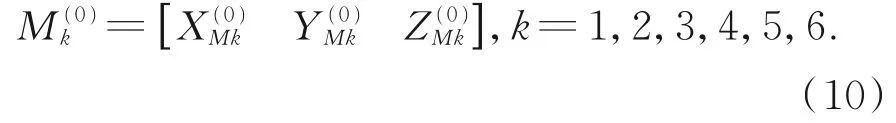
给定动平台位姿,记作:
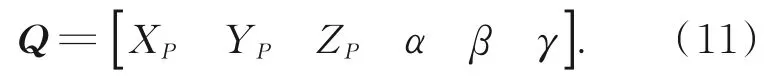
转换为齐次坐标变换矩阵形式[13],得到:

由式(3)及式(12)可得坐标系{E}在{B}的位姿,记作:
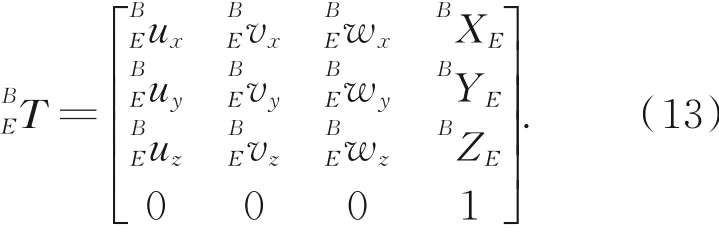
于是可得{E}的三个坐标平面I,II,III的平面表达式,记作:
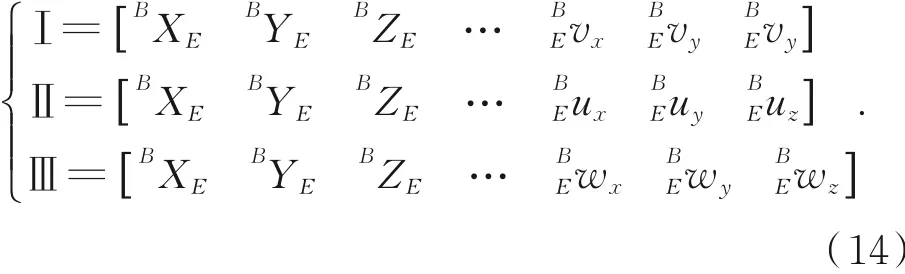
位移传感器直线方程与平面方程联立,可求出各传感器与各坐标平面的触点坐标,记做:
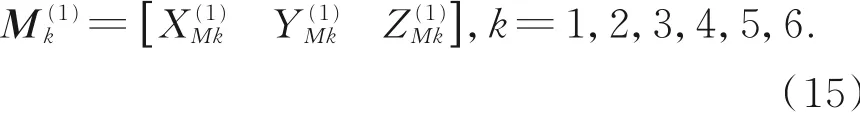
由式(10)与式(15)可得两触点间的直线距离:
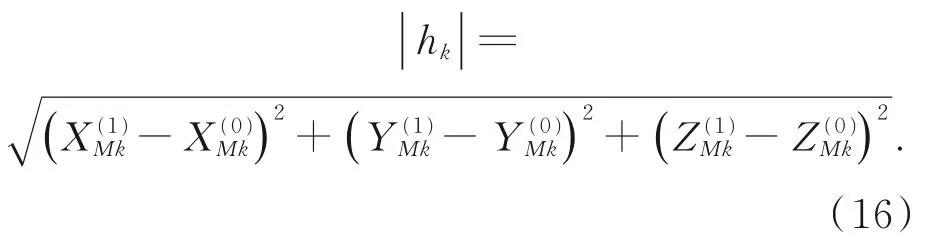
如果触点向坐标轴正向移动,规定h为正,反之为负,即:
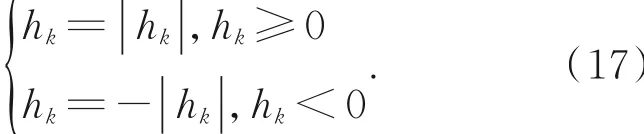
将各位移传感器的位移量写成向量形式,有:

由此,由动平台的位姿得到了各位移传感器的位移值,此即运动学正解。
2.4运动学逆解
设位姿改变后,各位移传感器伸缩量为hk,k=1,2,3,4,5,6。
此时位移传感器与Ⅰ,Ⅱ,Ⅲ面的触点也随之发生改变,在测量系中的坐标Mk为:
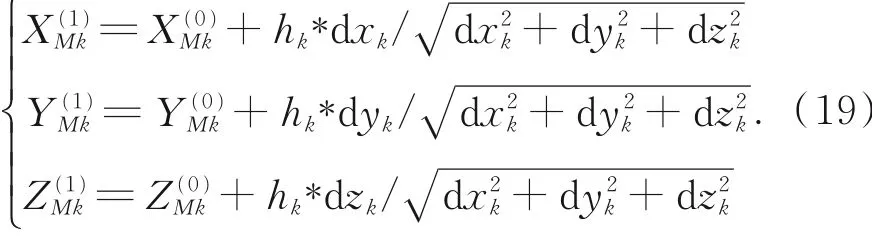
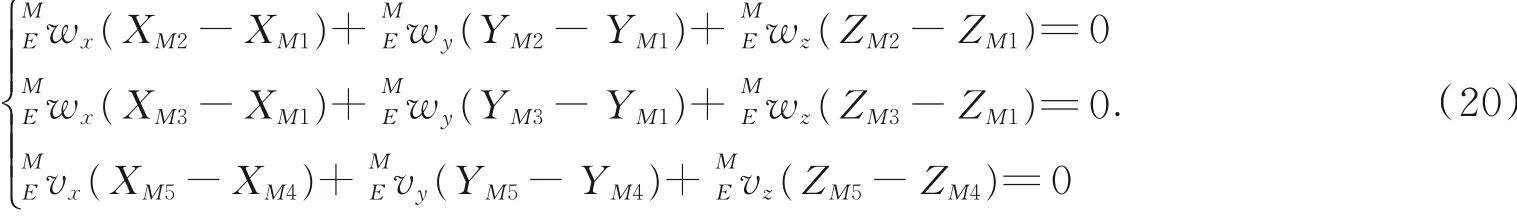
三平面法向量相互垂直,于是有:[11]
利用RPY角逆解公式,可得:
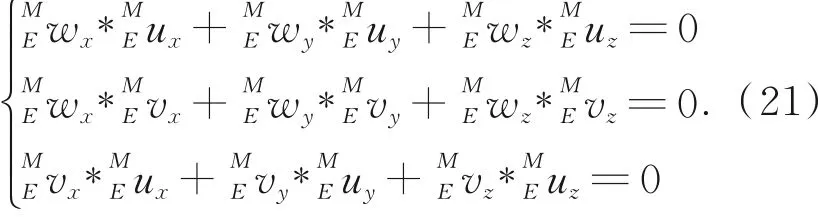
又由单位向量模为1,可得:

9个未知量,9个方程,未知量可求。于是可得Ⅰ,Ⅱ,Ⅲ面的编程表达式,记为:
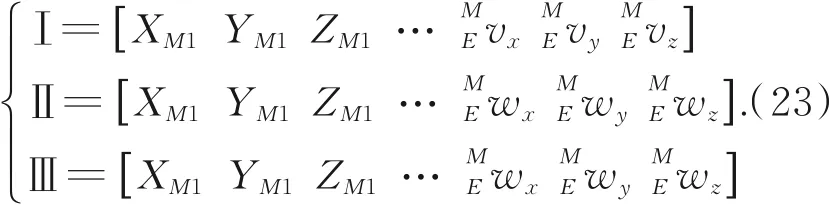
三平面表达式联立,可得三平面交点,记作:
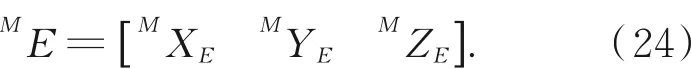
于是可得{E}在{M}的齐次坐标变换矩阵:

由式(1)可知:
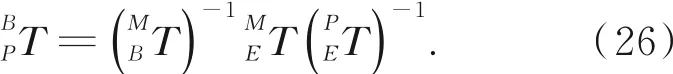
结果简写为:
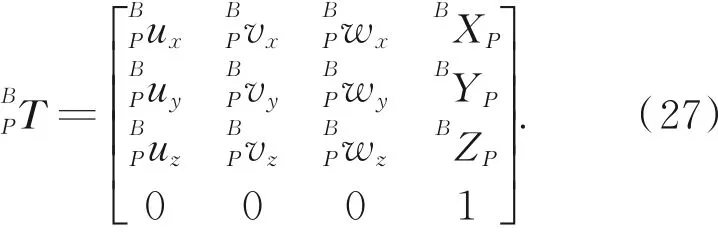
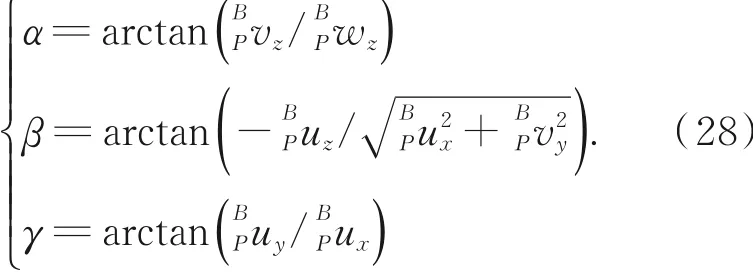
于是解算出动系在定系中的位姿,即正交位移测量系统的运动学逆解:
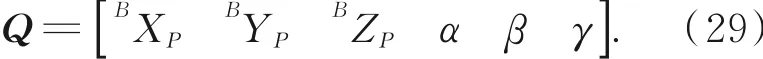
由位姿解流程可以看出,虽然整个过程稍显复杂,但测量数据需求量较小,易于操作。这是该测量方法的优势所在。
3 基于微小位移合成法的误差模型
动平台每变换一个位姿,针对每个位移传感器可构造一个约束方程,设:
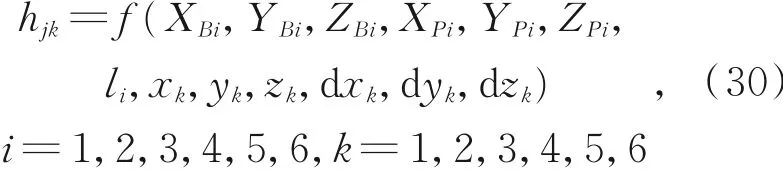
当结构参数出现误差时,方程变为:
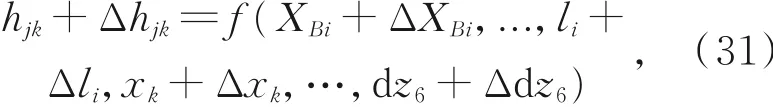
式中:j=1,2,3,…表示不同位姿,于是有:
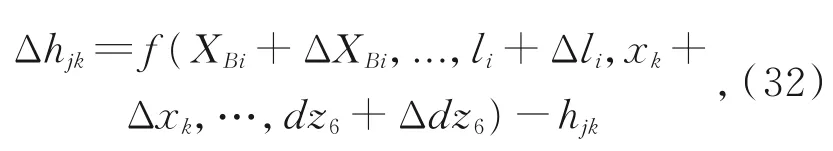
其中:ΔXBi,...,Δli,Δxk,…,Δdz6为并联机构及正交位移测量系统的结构参数误差,Δhjk为结构参数误差导致的位移传感器示值偏差。
由此,建立了基于微小位移合成法的并联机构与正交位移测量系统组合体的误差模型,模型中,Δhjk可通过位移传感器测量值与名义值做差得 到,XBi,YBi,ZBi,XPi,YPi,ZPi,li,xk,yk,zk,dxk,dyk,dzk为并联机构及正交位移测量系统的参数名义值,为已知量,ΔXBi,…,Δli,Δxk,…,Δdzk为未知量,求解上式即可得到各结构参数误差。
4 基于优化算法的参数误差辨识
4.1 参数误差辨识模型的建立
在获得了试验数据后,如何得到合理的运动学参数误差辨识结果是整个运动学标定的难点同时也是重点,对试验数据的处理采用不同的方法,就会得到不同的参数辨识结果。根据辨识模型的不同,参数误差辨识方法可分为两类:一种是基于线性误差模型的辨识方法[15-17],该方法通过辨识雅克比矩阵建立结构参数误差与误差测量结果之间的函数映射关系,并对该模型进行求解从而辨识出结构参数,可归结为典型的线性方程组求解;实际应用过程中,需要并联机构沿固定轨迹运动,灵活性低且计算量大。另一种是基于优化算法的参数误差辨识方法,该方法不建立线性的误差模型,利用优化算法直接搜索运动学参数误差的辨识方法,这类方法基于机器的运动学方程及误差测量结果,没有具体的辨识方程,是一类典型的非线性方程求解问题,常见的求解方法如遗传算法[18]、神经网络[19]等等。
本文中的误差模型为非线性,无法构建线性方程组来求解结构参数误差,只能采用第二种方法。
上述模型的参数误差辨识问题可转换为使目标函数最小化的最优化问题。构造最优化问题数学模型如下:
以各位姿下传感器示值误差的平方和最小为目标函数,即:
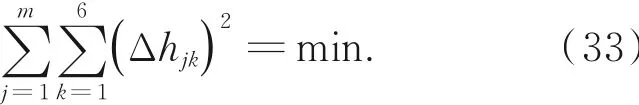
以并联机构和标定装置的结构参数误差为设计变量,即
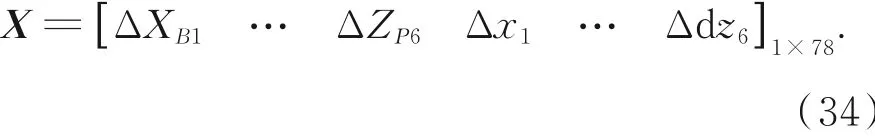
各变量约束条件为现有加工及装配能力下变量的取值范围,取±0.2 mm/rad。
4.2 优化工具的选择
结构参数误差的辨识,就是从设计变量的取值范围内搜索出满足式(33)的解,使用最简单的随机搜索即可完成这个工作,但随机搜索计算速度慢,计算量大。以遗传算法为代表的优化算法虽具有全局搜索、稳定可靠、无需方程求解等特点,但这些算法计算量大,计算时间长,无法处理昂贵约束,且容易陷入局部最优解。而新一代智能优化设计软件OASIS奥希思为求解以上方法提供了一个有效的途径。OASIS(Optimization Assisted System Integration Software),即优化辅助系统集成软件,集成了业界领先的AI算法,能自动运行仿真软件,自动改变输入文件,重新启动设计流程,从而消除了传统开发设计流程中的瓶颈,使整个设计流程实现全数字化和全自动化,能更快速,更高效地解决一系列的设计优化问题[20]。
综上,本文将尝试利用该软件对参数误差进行辨识。
5 并联机构的参数标定试验
为验证上述方法有效性,开展了并联机构的参数标定试验。
5.1 标定对象及标定试验要素
本文的参数标定对象为一套六自由度6-SPS并联机构,如图3所示。结构参数见表1。标定试验要素包括六支位移传感器,传感器座、被测基准块等,如图4所示,其中位移传感器采用捷克ESSA光栅位移传感器SM30系列,具有量程大、分辨率高、准确度高等优点[24]。
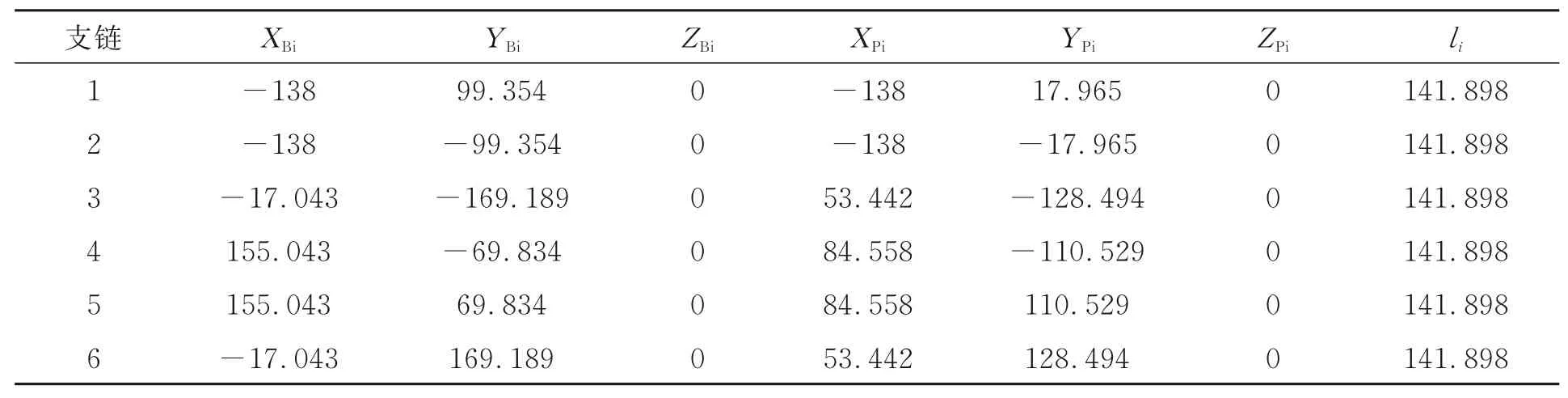
表1 6-SPS并联机构42项运动学参数名义值Tab.1 Nominal value of 42 kinematic parameters of 6-SPS parallel mechanism (mm)

图3 六自由度并联机构Fig.3 Photo of 6-DOF 6-SPS parallel mechanism

图4 SM30系列ESSA光栅位移传感器Fig.4 SM30 series ESSA grating displacement sensor
5.2 标定试验过程
开展基于321型正交位移测量系统的标定试验,试验现场照片如图5所示,位移传感器S1,S2,S3位于被测基准块的+Z方向,S4,S5位于被测基准块的-Y方向,S6位于被测基准块的-X方向,数显表1显示的是S1,S2,S3的数据,数显表2显示的是S4,S4,S6的数据。
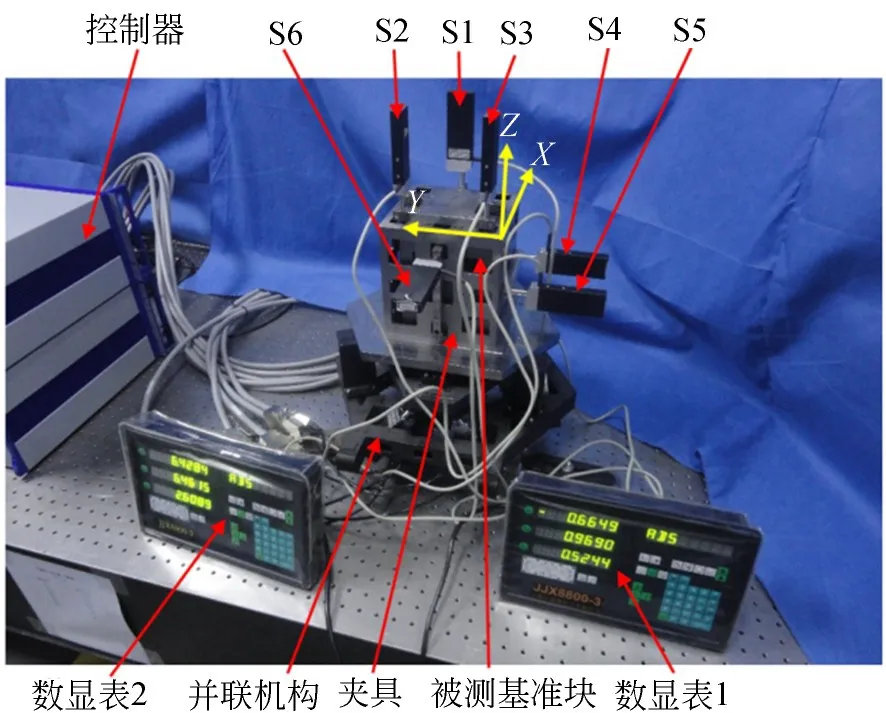
图5 321型正交位移测量系统的数据采集现场Fig.5 Photo of data collection of type 321 orthogonal displacement measurement system
共选取18个位姿组成的量测配置,详见表2,对应18组位移传感器的理论值,详见表3,开展位移测量,位移传感器示值详见表4。
根据上述数据,建立基于OASIS奥希思的优化模型,变量为并联机构及正交位移测量系统的结构参数误差,取值范围为±0.2 mm/rad,步长为0.001 mm/rad,目标函数为各位姿下传感器示值误差的平方和最小,在OASIS奥希思中开展寻优计算,流程如图6所示,计算过程见图7。经过200多轮迭代,得到并联机构及正交位移测量系统的结构参数误差,进而得到补偿后的结构参数。补偿后并联机构的结构参数详见表5。
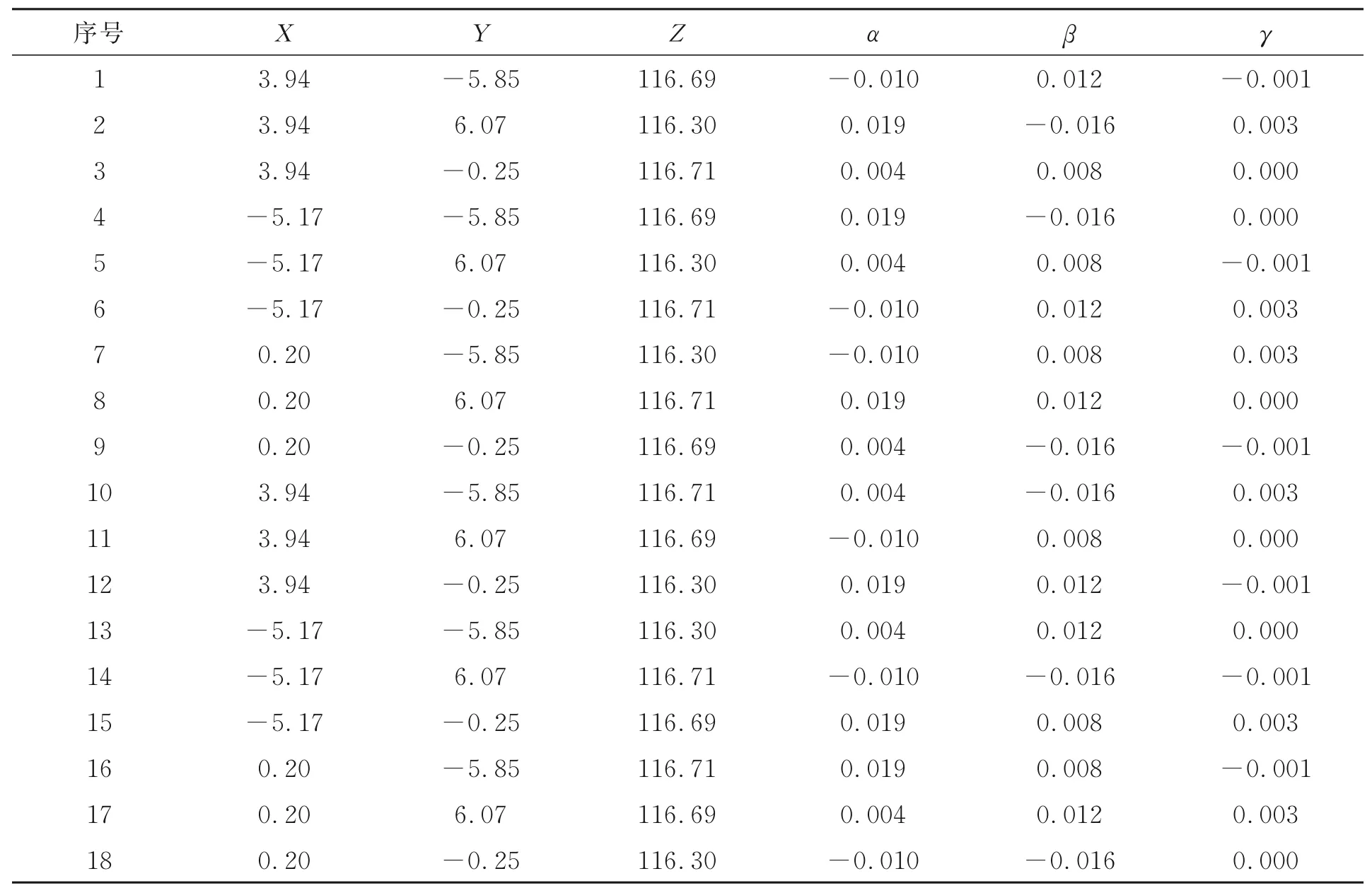
表2 标定试验的量测配置Tab.2 Measurement configurations of calibration experiment (mm·rad-1)
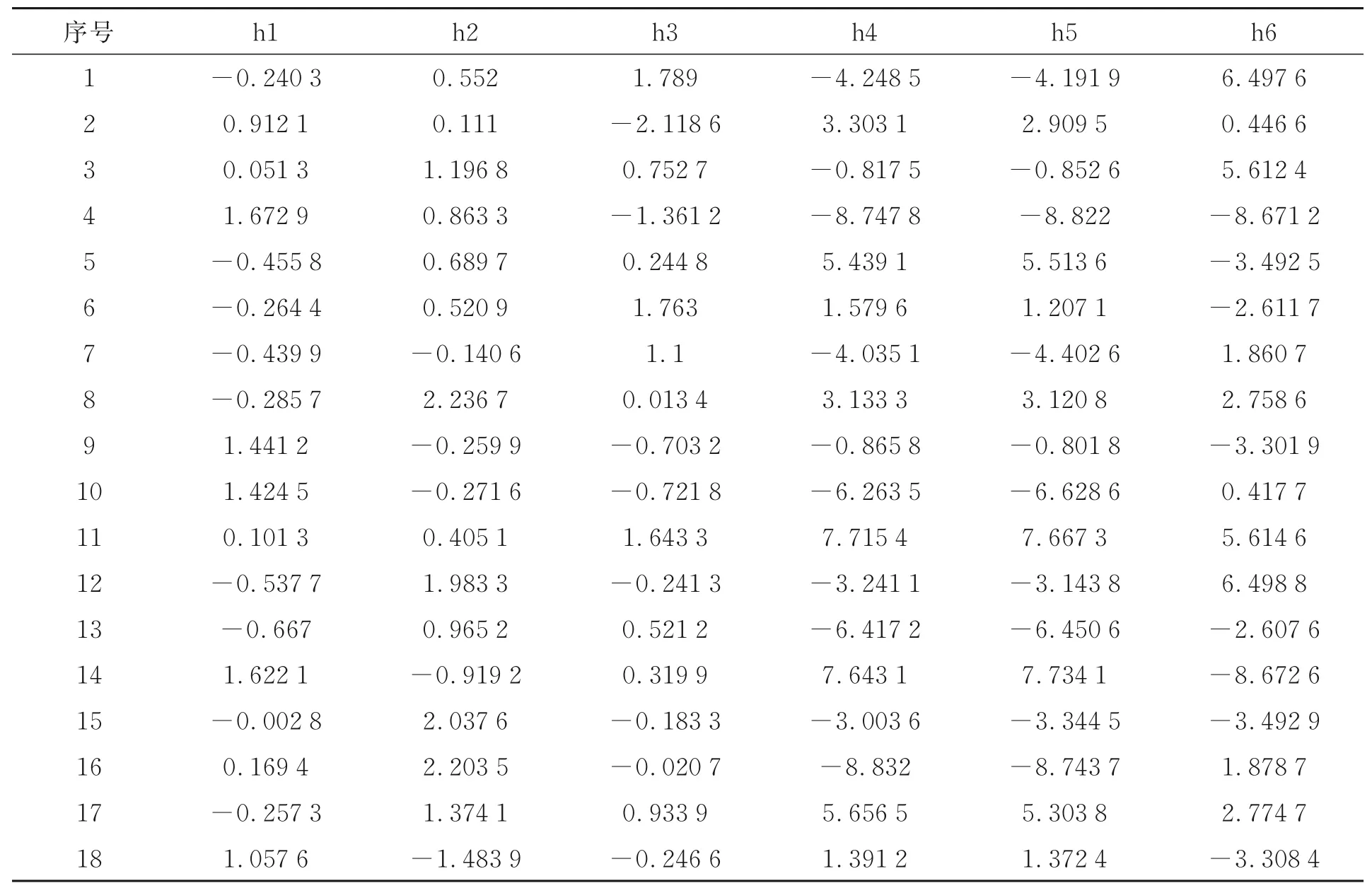
表3 标定试验位移传感器名义值Tab.3 Nominal value of displacement sensor of calibration experiment (mm)
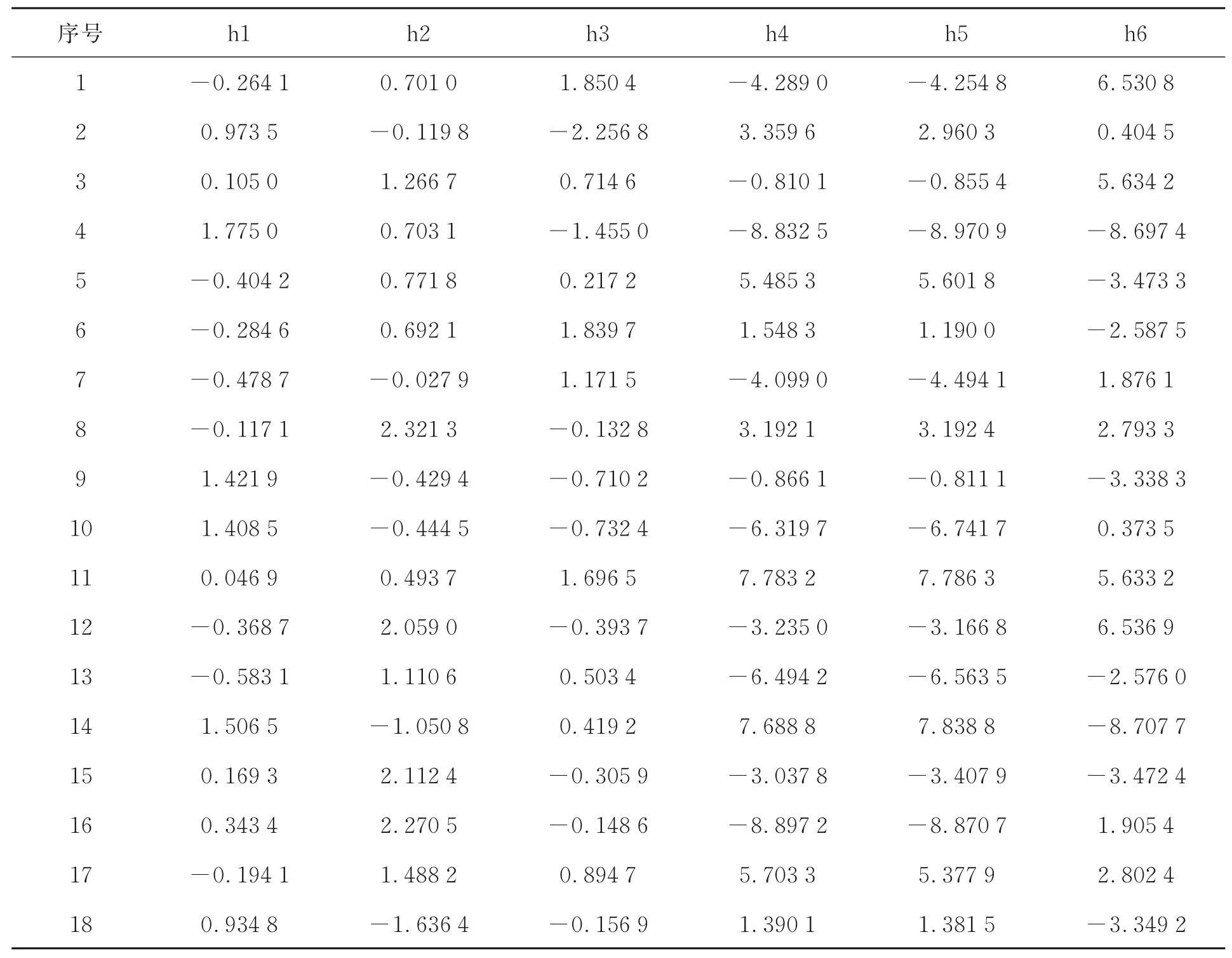
表4 标定试验位移传感器测量值Tab.4 Measurement value of displacement sensor of calibration experiment (mm)
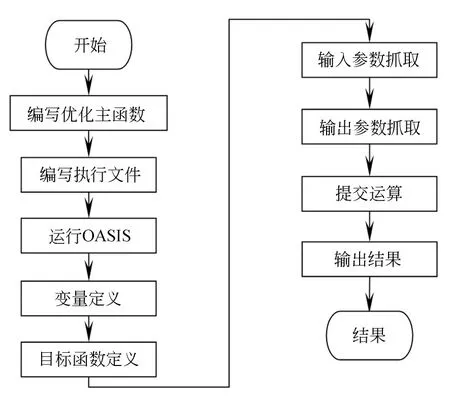
图6 优化流程Fig.6 Flow chart of optimization
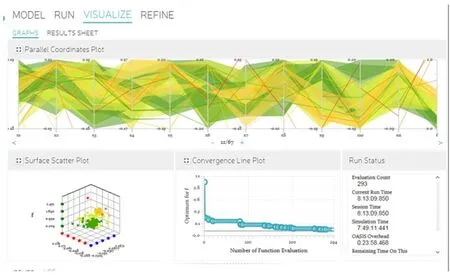
图7 OASIS奥希思可视化计算过程Fig.7 Visual calculation progress in OASIS
修改并联机构控制程序中的参数,再分别输入标定试验的位姿,使动平台运至指定位姿,验证标定效果。将补偿前后的正交位移测量系统结构参数、位移传感器示值代入正交位移测量系统运动学逆解,得到补偿前后位姿误差,如图8所示。
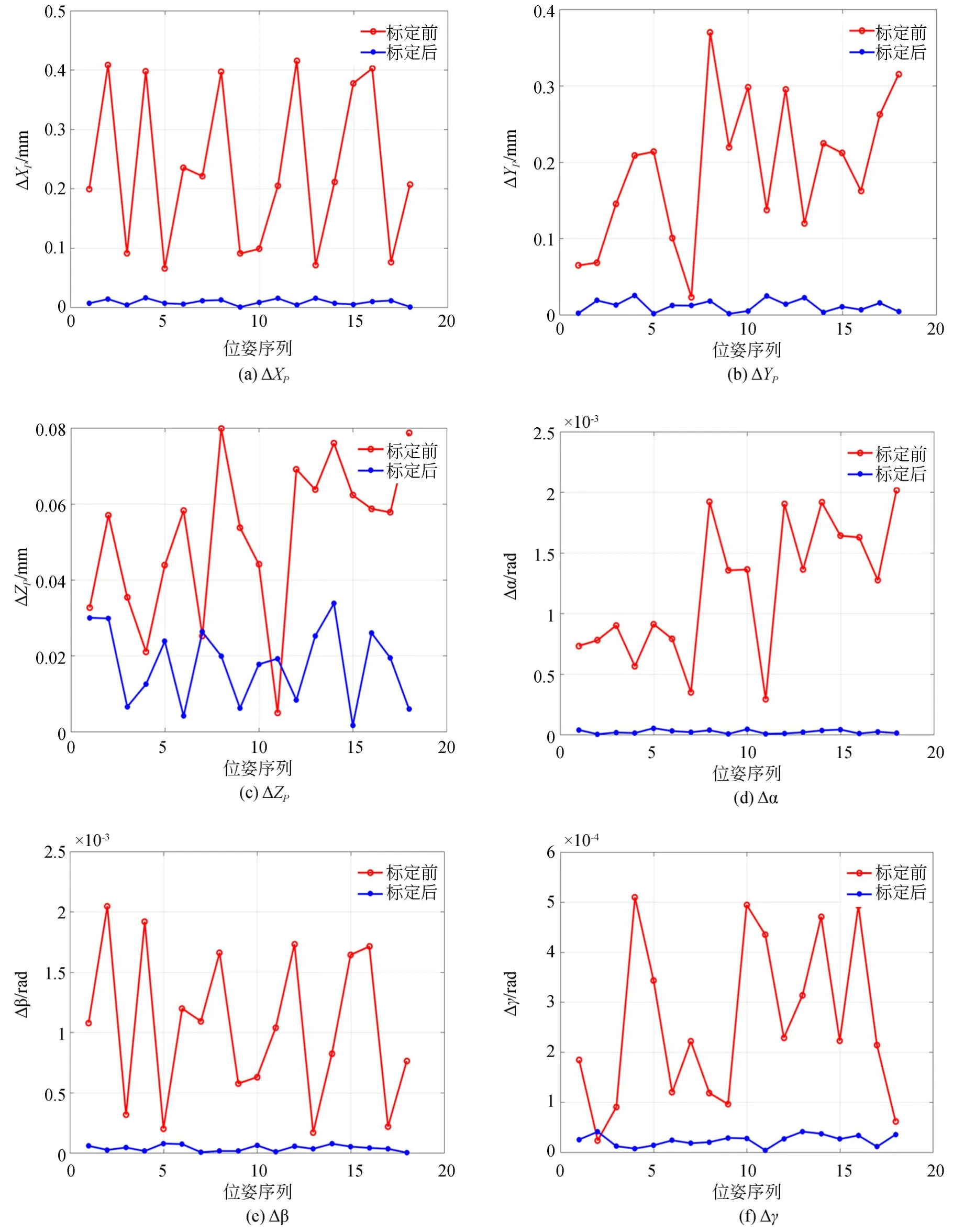
图8 标定前后的位姿误差Fig.8 Pose error before and after calibration
由图8可知:
(1)对于ΔXP,最大误差标定前约为0.42 mm,标定后约为0.016 mm,降低了约96%;
(2)对于ΔYP,最大误差标定前约为0.37 mm,标定后约为0.025 mm,降低了约93%;
(3)对于ΔZP,最大误差标定前约为0.08mm,标定后约为0.034 mm,降低了约58%;
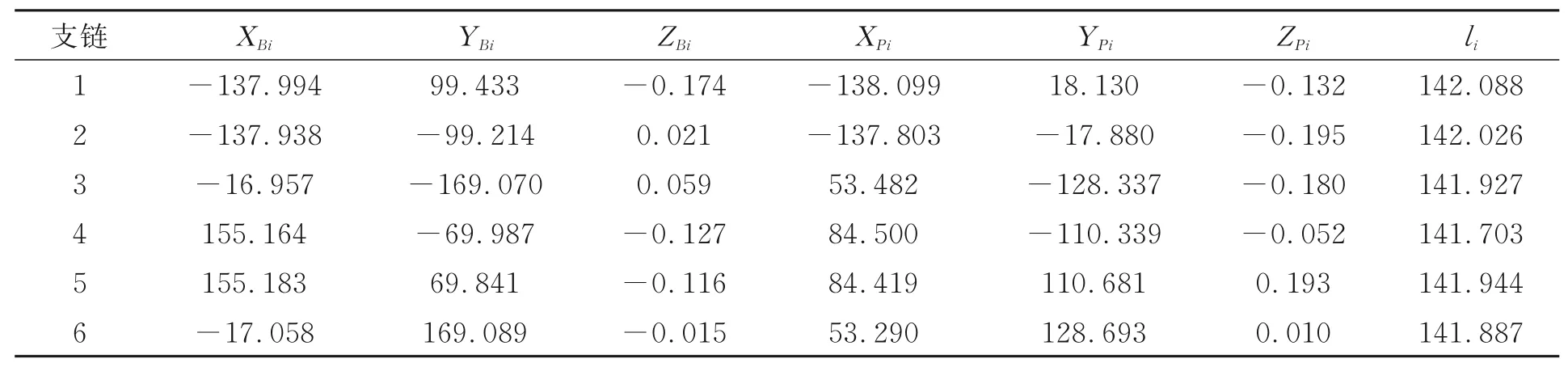
表5 补偿后的42项运动学参数Tab.5 42 kinematic parameters after compensation (mm)
(4)对于Δα,最大误差标定前约为2×10-3rad,标定后约为5×10-5rad,降低了约97%;
(5)对于Δβ,最大误差标定前约为2×10-3rad,标定后约为8×10-5rad,降低了约96%;
(6)对于Δγ,最大误差标定前约为5×10-4rad,标定后约为4×10-5rad,降低了约92%。
综上,标定后的位姿误差明显低于标定前,说明标定效果显著。
与传统的测量设备或测量方法相比,本文提出的位姿测量装置及方法存在以下优势:
(1)易于操作。只需将被测基准块固定在并联机构动平台上,将位移传感器固定在夹具上,即可开展位姿测量。
(2)简洁高效。只要并联机构末端位姿发生改变,位移传感器示值就会发生变化,将其代入运动学逆解,即可获取末端位姿信息,极大地节省了人力成本和时间成本。
(3)成本低廉。测量系统主要组成部分为:六支高精度位移传感器(可重复使用)、被测基准块及测量基准块,除此之外,或许还需要一些位移传感器夹具,总体成本相对较低。
总之,本文提出的位姿测量装置及方法不仅能有效提升并联机构的定位精度,而且具有易于操作、简洁高效、成本低廉等优点。
6 结 论
为了简化六自由度并联机构的参数标定过程,提高标定效率,降低标定成本,本文提出了基于正交位移测量系统的位姿测量方法,利用空间解析几何的方法,分析了正交位移测量系统的运动学正解与逆解。利用微小位移合成法,建立了并联机构与正交位移测量系统组合体的误差模型。为辨识并联机构的结构参数,构造了最优化问题数学模型,目标函数为传感器示值误差的平方和最小,设计变量为并联机构和标定装置的结构参数误差。搭建了基于正交位移测量系统的并联机构标定平台,对待测六自由度并联机构进行了位移测量,利用OASIS奥希思软件对并联机构的结构参数误差进行辨识,对结构参数进行补偿,并对补偿效果进行了验证。标定前后位姿误差对比表明:最大位置误差降低了58%~96%,最大姿态误差降低了92%~97%,有效提升了并联机构的定位精度。与传统的标定方法相比,该方法具有易于操作、简洁高效、成本低廉等优点,可有效简化标定工作,提升标定效率、降低标定成本。
本文的研究结果对并联机构的标定具有较高的指导意义和参考价值。
致谢:论文撰写过程中,得到了OASIS奥希思技术顾问苏龙聚和李毅的技术支持,在此表示深深的谢意。

