多局域空心光阱及其光场调控

林兴磊，付文升，邹永刚，张 贺*，吕金光

（1.长春理工大学光电工程学院高功率半导体激光国家重点实验室，吉林长春130022；2.中国科学院长春光学精密机械与物理研究所应用光学国家重点实验室，吉林长春130033）

1 引 言

局域空心光束是沿光传播方向上有着强度为零而区域外三维空间都围绕着高强度光的一种空心光束［1］。局域空心光束的三维封闭暗中空区域可以对微粒进行捕获及操纵，因此在光镊［2］、光学扳手［3］、激光导管［4］、激光囚禁［5］和光学微操控［6］等方面有着广泛的应用。尤其将局域空心光束作为操纵微粒的捕获光束时，它有着非接触、低损伤等优点，使操纵活体物质成为可能，并已成功地应用在生物医学领域［7］。作为光镊技术的发明者，Ashikin获得了2018年诺贝尔物理学奖，并把光镊的研究推向了高峰。

相对于单局域空心光束，多局域空心光束具有多个光阱，可同时对多个粒子进行捕获和操纵，在现代光学以及生物医学中具有很大的应用潜力。目前，产生多局域空心光束的方法主要有贝塞尔光束干涉法［8］、平面波与贝塞尔光束干涉法［9］和几何光学方法［10］等。2006年，Ahluwalia等人［11］设计了一个高效率的双轴棱镜产生不同径向波矢量的贝塞尔光束，干涉形成三维周期性局域空心光束。2012年，程治明等人［12］利用贝塞尔光束与球面波叠加得到多个具有高强度梯度的局域空心光束，与两束贝塞尔光束干涉产生的多局域空心光束相比，在暗域处有着更大的光强梯度，更有利于稳定的粒子囚禁。2017年，王志章［10］等人基于几何方法，利用多个不同厚度的ZnSe晶体设计光学系统，产生的多局域空心光束可以灵活调节，可用于一些较大尺寸粒子的光学非接触式囚禁与操控。形成周期性局域空心光束的方法有很多，大多集中在单个局域空心光束的粒子囚禁［13］，但对多光阱操纵的研究却鲜有报道。与多光阱的操纵机制相同，可以把多光阱操纵视为多个单光阱操纵，从而扩展到多光阱囚禁［14］。本课题组经过多年的局域空心光束研究，在产生方法和粒子操纵方面取得了一些成果［15］。我们利用几何光学系统的设计形成数量有限的局域空心光阱，作为光镊来操纵从纳米级到毫米级的多种微观粒子，具有一定的实际意义。

本文针对多局域空心光束，生成局域空心光束的空心四阱。通过调控两个反射镜的偏转角度变换光阱位置，对其中单个光阱的梯度力和散射力进行了模拟计算，采用蒙特卡罗法验证粒子轨迹最终局限于光阱中心的极小区域内，从而为多局域空心光束囚禁和操纵微粒的研究提供一种简单有效的方法。

2 原 理

2.1 空心四阱系统设计

如图1所示，双管半导体激光器发出的两束激光，经过非球面透镜和柱面透镜［15-16］的准直和整形，入射到空心整形棱镜中，得到的空心光束经过分光棱镜后分为两束，再经过特定角度的反射镜后叠加形成空心四阱。其中，双管半导体激光器是利用min-bar芯片切割而成的双管光源［17］，作为阵列激光器的一个基础单元，具有普适性。

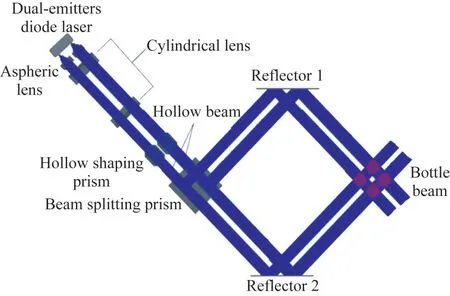
图1 空心四阱系统Fig.1 Bottle four-trap beam system

2.2 空心整形棱镜设计及光学系统分析

经过准直后的激光束平行入射到空心整形棱镜中，本文为简化计算，把空心整形棱镜看作负-正轴棱锥系统［18-19］。根据几何关系建立二维y-z坐标系，以棱镜的左边角顶点为坐标原点，传输方向为z的正向，激光光束（λ=632.8 nm）入射到负轴棱锥产生无衍射的贝塞尔光束［20］，光束经过正轴棱锥会产生空心高斯光束，如图2所示。空心整形棱镜的顶角为90°，材料为F_SILICA，折射率为1.46，两个轴棱锥之间的距离为1.15 mm，空心整形棱镜的长度为2.15 mm，入射空心整形棱镜的光束直径为0.4 mm，从空心整形棱镜出射的空心高斯光束的外宽直径为1 mm，内宽直径为0.616 mm。

入射到空心整形棱镜的光束可以近似为类高斯光束分布，即有：

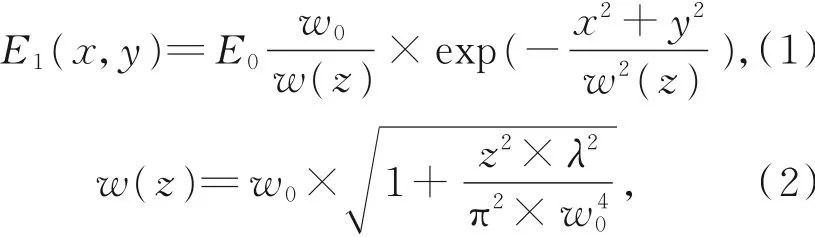
式中：w0为激光光束的束腰半径，λ为入射光束的波长。为简化计算，E0=1，负、正轴棱锥传输矩

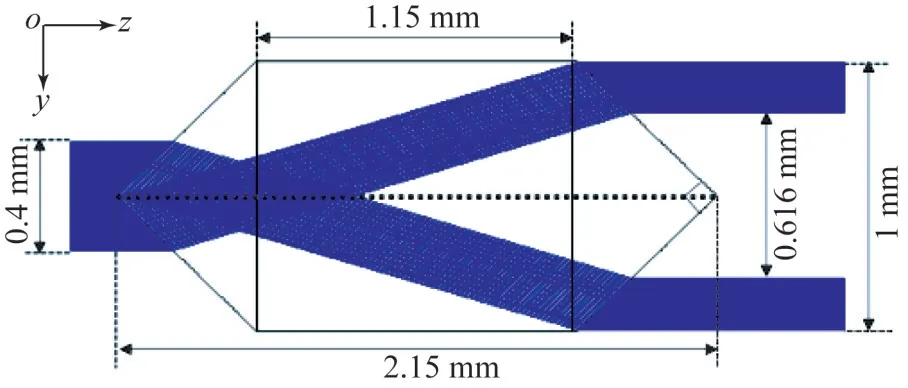
图2 空心光束系统Fig.2 Bottle beam system

阵分别为：

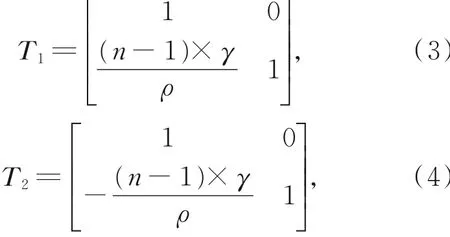
其中：n为空心整形棱镜的折射率，γ为空心整形棱镜的底角，ρ为轴棱锥所在平面的径向坐标。根据柯林斯公式，通过负轴棱锥和正轴棱锥的光场分布分别为：

根据上述公式仿真模拟了空心整形棱镜不同位置处的光场分布，如图3所示。

3 结果与讨论

3.1 光阱位置调控

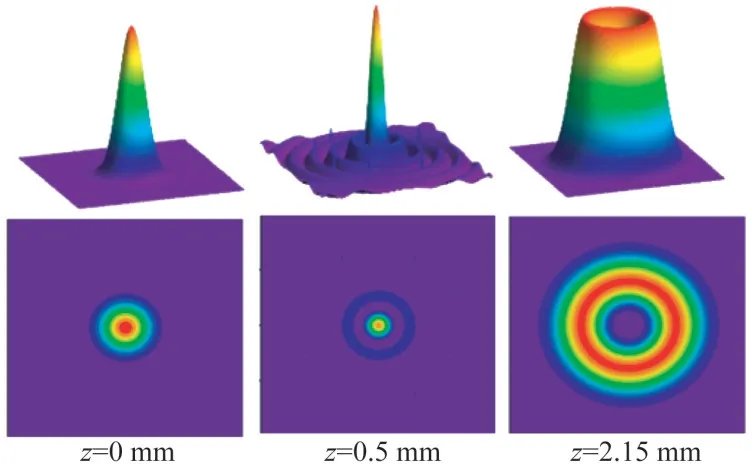
图3 不同位置处的光场分布Fig.3 Light field distribution at different locations

如图4所示，由空心整形棱镜出射的空心光束，通过分光棱镜后分为两边，分别经过偏转角度为θ1的反射镜R1和偏转角度为θ2的反射镜R2，反射叠加之后形成空心四阱。这里选取了5组不同偏转角度，仿真模拟了空心四阱光学系统的变化。其中，当偏转角度（θ1，θ2）为（100°，10°），空心四阱变化为空心十二阱，光阱数量的增加可以提高多局域空心光阱系统的利用效率。这12个光阱产生的囚禁效果是不完全相同的。反射镜之前的8个光阱是由未发生反射的空心高斯光束和发生了反射的空心高斯光束进行叠加形成的。反射镜之后的4个光阱是由两个都发生了反射的空心高斯光束进行叠加形成的。光束在反射过程中伴随着能量的损耗，所以反射镜之前的8个光阱的四周阱壁能量是不同的，而反射镜之后的4个光阱的四周阱壁能量是完全一样的。当反射镜之前的8个光阱被使用后，反射镜之后的4个光阱虽然可以正常囚禁微粒，但是不能移动位置，因此形成的局域空心光束对微粒的力学作用是不同的，需要根据微粒的不同性质选择适合的光阱进行囚禁和操纵。

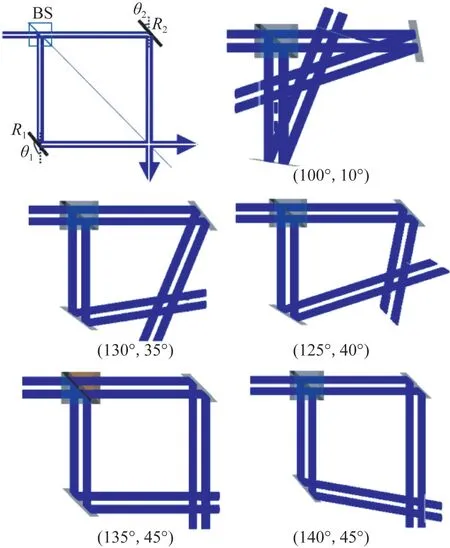
图4 不同旋转角度时的光阱位置Fig.4 Optical trap position for different angles of rotation

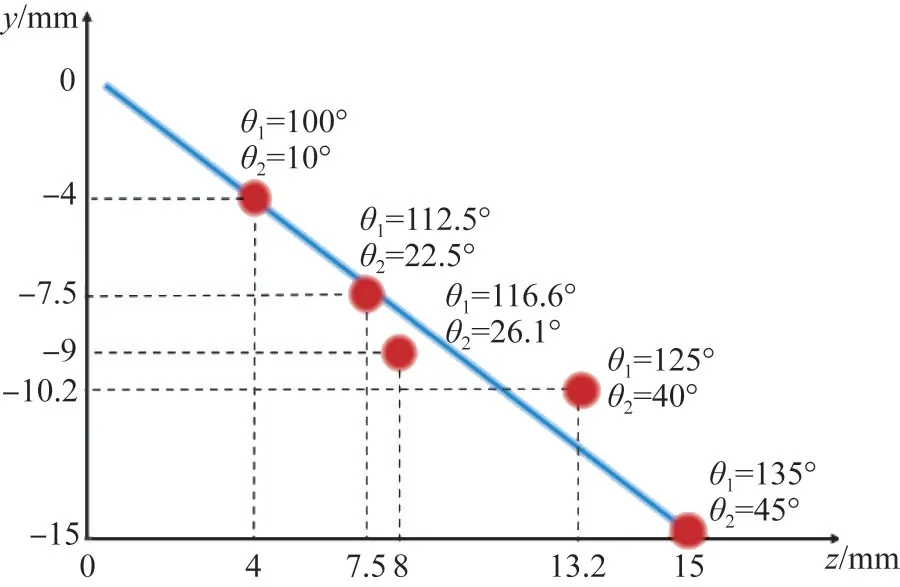
图5 光阱位置与偏转角度的关系Fig.5 Relationship between optical trap position and deflection angle

根据局域空心光阱位置和反射镜偏转角度的依赖关系，绘制y-z轴坐标系，如图5所示（彩图见期刊电子版）。偏转角度满足θ1－θ2=90°时，光阱位置在蓝线上移动；偏转角度θ1＜112.5°和θ2＜22.5°时，光阱数量由4个变为12个。光阱位置为（4，4）和（－15，15）时，对应偏转角度分别为（100°，10°）和（135°，45°），两组光阱位置都在蓝线上，此时两组偏转角度有一定规律，即相减为90°。当光阱为任意位置（－9，8）和（－10.2，13.2）时，对应的偏转角度分别为（116.6°，26.1°）和（125°，40°），坐标系中的任意光阱位置都可以找到偏转角度并一一对应，光阱捕获粒子具有精准性和灵活性。粒子是跟随光阱的空间位置变化而变化的，并且移动过程中粒子受力产生运动。实现上述变化的前提是必须保证光阱位置的变化保持在一条直线上，才能使得粒子在光阱移动位置的过程中不发生逃逸。根据y-z轴坐标系的几何关系，推导反射镜偏转角度和光阱位置坐标（y，z）的计算公式，得到：

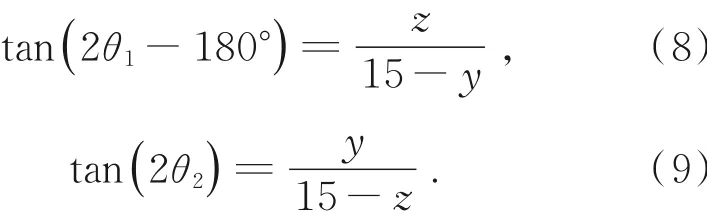
当粒子捕获操纵时，首先需要确定粒子的位置，即确定了光阱要移动的位置，建立坐标系并标记粒子位置的坐标，根据位置坐标和偏转角度的关系和公式，得出两个反射镜需要偏转的角度，通过调控反射镜的偏转角度，使光阱位置移动到粒子位置，从而捕获和囚禁微粒，达到精确捕获粒子的目的。

3.2 光阱力

瑞利粒子是指尺寸远小于光波长的粒子，通常认为尺寸小于光波长的二十分之一就是瑞利粒子。光束与瑞利粒子发生作用产生辐射力，辐射力包括梯度力和散射力。其中，梯度力是由光强分布不均匀引起的，散射力是由粒子对光吸收再辐射后引起的光子动量变化而产生的。

选取θ1=135°和θ2=45°时的情况，研究瑞利粒子处于光阱中的受力。粒子处于光阱中时，梯度力和散射力同时作用于微粒，其中梯度力起主要作用，将粒子稳定在光阱中心。当反射镜变换偏转角度，使得空心光阱的位置发生改变时，光阱中的梯度力依旧起主要作用，可以将微粒囚禁在光阱中，所以选取θ1=135°和θ2=45°分析粒子的受力情况具有普遍性。此时，四束空心光束叠加形成4个完全相同的光阱。其中，单个光阱的形貌如图6（b）所示，而粒子的受力情况如图6（c）所示。为了清晰地观察光阱内粒子的受力情况，需要把光壁去掉。光壁对微粒的作用力表现为梯度力，方向指向光阱中心，而散射力的方向为光传播方向，即两个散射力的方向分别为y正方向和z正方向，重力方向为x轴的负方向，瑞利粒子受合力作用向光阱中心移动。

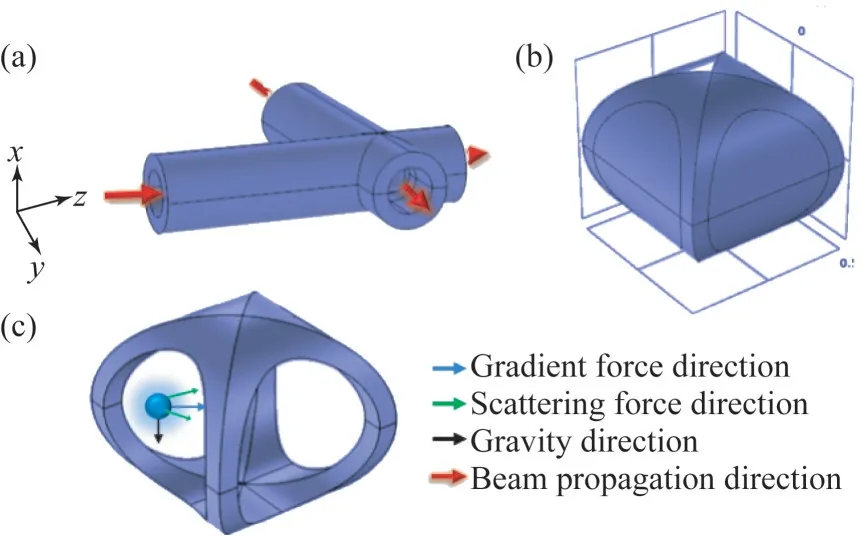
图6 光阱分析。（a）单阱传输示意图；（b）单阱示意图；（c）无光壁的单阱内粒子示意图Fig.6 Analysis of optical trap.（a）Transmission diagram of single trap；（b）Schematic diagram of single trap；（c）Schematic diagram of the particle in a single trap without light wall

根据理论分析，计算得出单个光阱处的光强为：

梯度力和散射力［21］分别为：

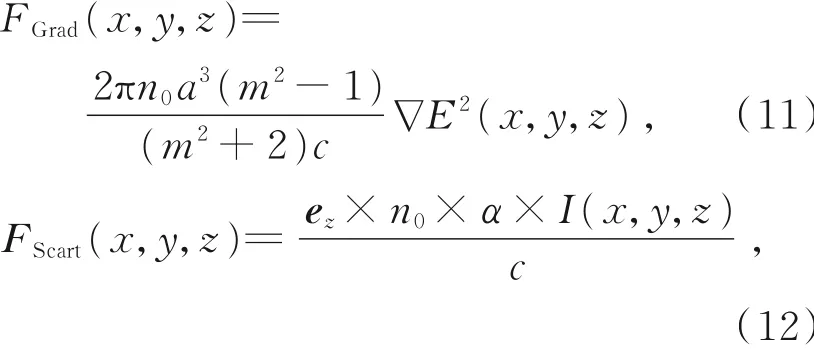
其中：ez为沿着光传播的单位矢量，而I（x，y，z）=n0ε0c|E（x，y，z）|2，ε0为真空中的介电常数，m=n1/n0，n0为环境折射率，n1为粒子折射率，a为粒子半径，c为真空中的光速，激光功率为100 mW。所选瑞利粒子为乙酰苯液体的水分子，粒子半径为20 nm，所处环境为乙酰苯液体，水分子折射率n1为1.33，液体环境折射率n0为1.53。乙酰苯液体的水分子团尺寸小于激光波长（632.8 nm）的二十分之一，符合瑞利粒子的选取条件。另外，水分子团位于液体环境中，所受的光阱力只有辐射力（梯度力和散射力），可以忽略空气中光泳力的干扰，保证研究和计算的准确性。

如图7所示，梯度力的数量级10－14N远远大于散射力的数量级10－19N，当粒子处于光阱中时，梯度力和散射力同时作用于微粒，将粒子稳定在光阱中心。根据图2中对空心整形棱镜的分析，得出空心光束的内宽直径为0.616 mm，所以空心光束的光斑直径为0.616 mm，二维光阱的位置为（－0.3 mm＜x＜0.3 mm，－0.3 mm＜y＜0.3 mm）。由图7（a）可知，当－0.3 mm＜y＜0时，粒子受力为正，光阱驱动粒子往y=0的光阱中心移动；当0＜y＜0.3 mm时，粒子受力为负，光阱驱动粒子也往y=0的光阱中心移动，最终在光阱中心保持平衡。根据文中的计算和研究分析，得出梯度力远远大于散射力和重力。理论上计算光场中梯度力的分布并进行积分，得出光的势阱深度远大于梯度力，即梯度力形成的势阱足以克服布朗运动。结合梯度力可以平衡散射力和重力，所以可以判定粒子被稳定囚禁。

20 nm的水分子团的重力为10－19N，远远小于梯度力。采用蒙特卡罗法［21］模拟水分子在二维光阱中的运动过程。在室温条件下，设定时间为200 s，步长为0.01，粒子初始时刻的中心范围设置为光阱的范围，即（－0.3 mm＜x＜0.3 mm，－0.3 mm＜y＜0.3 mm），粒子设置为500个颜色不同的水分子团，通过不同颜色可以清晰地表达出粒子在光阱中反复振荡的现象。经过Matlab编程模拟，所得结果如图8所示，水分子被囚禁于x-y坐标系中（－0.09 mm＜x＜0，－0.01 mm＜y＜0.07 mm），即局限于光阱中心的极小区域内。由于水分子所受的梯度力远大于所受的散射力和重力，所以在囚禁过程中梯度力起主要作用。但是由于光阱中心的梯度力达到平衡，而散射力和重力的合力指向x-y平面的右下区域，因此在x-y平面内，粒子在光阱中心右下区域内振荡。在实验中，可以通过多个单物镜的显微成像方法观测捕获微粒，收集的图像较为精确，但不能快速实时成像；也可以通过三维成像技术进行观测，能够同时观测多个粒子，但是成像速率较低。

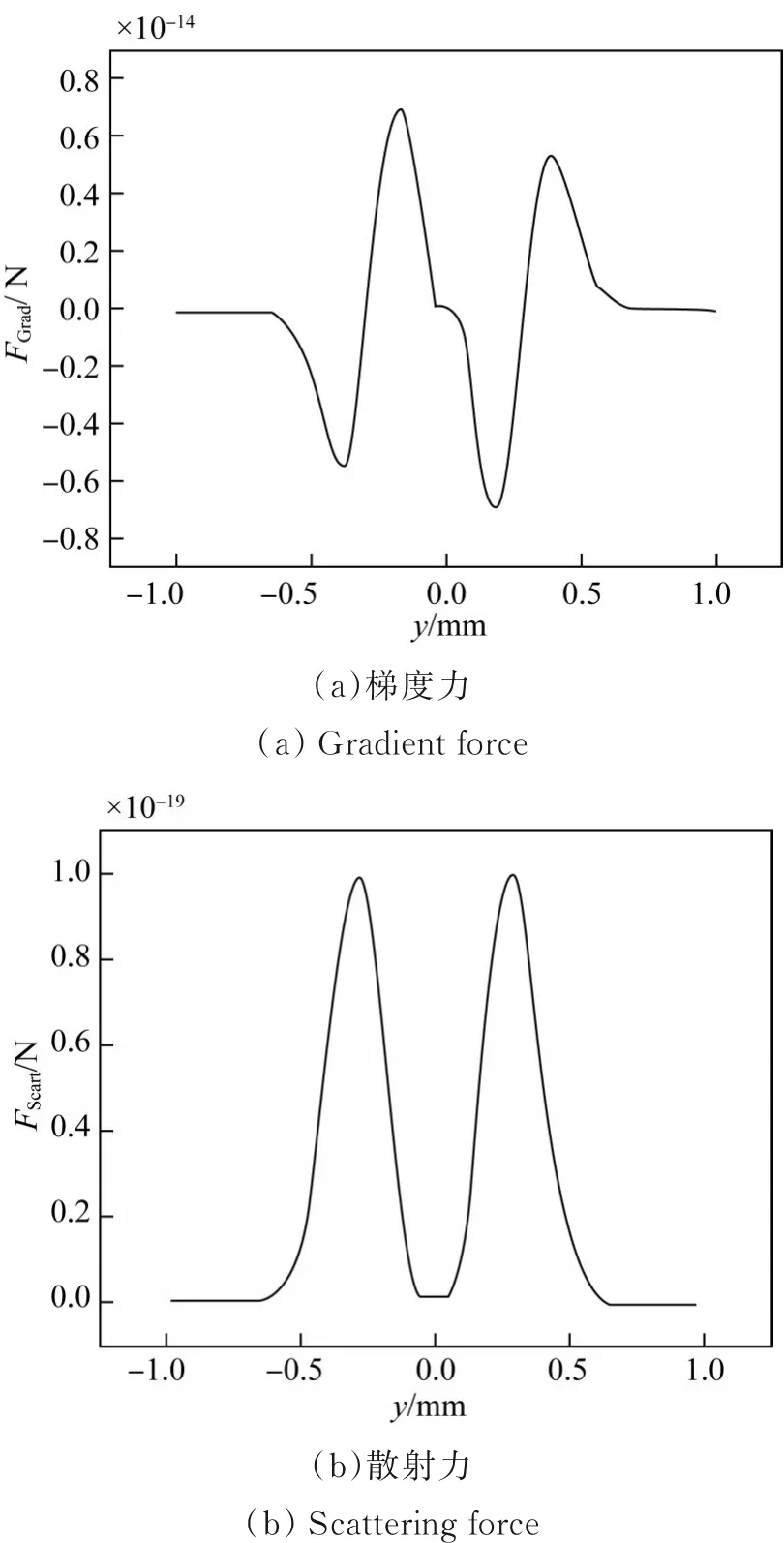
图7 梯度力和散射力的分布曲线Fig.7 Distribution curves of gradient force and scattering force

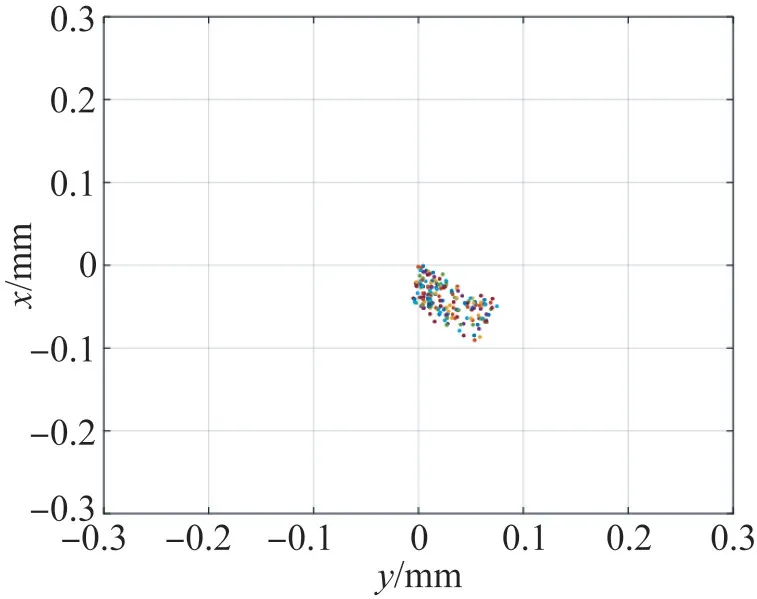
图8 蒙特卡罗法模拟结果Fig.8 Simulation result of Monte Carlo method

4 结 论

本文针对空心四阱的光学系统，利用反射镜的偏转角度调控空心四阱的几何位置，并对瑞利粒子受到的辐射力和囚禁效果进行了研究。绘制了y-z坐标系，调控反射镜的偏转角度研究光阱位置变化，光阱位置为（4，4）和（－15，15）时，对应的偏转角度分别为（100°，10°）和（135°，45°），此时的两组偏转角度有一定规律，即θ1和θ2相差90°，坐标系中的任意光阱位置都可以找到偏转角度并一一对应，实现光阱捕获粒子的精准性和灵活性。对单个光阱的辐射力进行研究，发现梯度力的量级在10－14，远远大于散射力和重力的量级（均为10－19），在光学捕获中起主导作用，满足粒子稳定囚禁的条件。最后，采用蒙特卡罗法分析和验证瑞利粒子的运动过程，运动轨迹最终局限于－0.09 mm＜x＜0，－0.01 mm＜y＜0.07 mm内，符合光场的理论分析。