快照式光谱光场成像技术

吕晓波，刘宇丰，李毅威，朱帅帅，林 杰*，金 鹏*

（1.哈尔滨工业大学仪器科学与工程学院，黑龙江哈尔滨150080；2.微系统与微结构制造教育部重点实验室（哈尔滨工业大学），黑龙江哈尔滨150080；3.西安航天动力试验技术研究所，陕西西安710100）

1 引 言

来自目标场景的光线携带着丰富的信息。Adelson和Bergen［1］首次提出使用全光函数P（x，y，z，θ，φ，λ，t）来表示这些信息，其中（x，y，z）表示空间维，（θ，φ）表示光线的传播角度，λ表示光的波长，t表示光子的发出时间。Gao和Wang［2］又加入了两维偏振信息（Ψ，χ），将该函数扩展到九维。传统的成像系统通常仅获取目标场景的空间二维信息（x，y），而忽略了其他维度的信息。光谱成像具备(x，y，λ)三维成像能力，光谱信息能够反映物质的化学和分子特性［3］，因此光谱成像被广泛应用于生物医学［4-5］、遥感［6］及食物质量检测［7］等领域。另一方面，目标物的三维空间信息（x，y，z）表征了其形态和位置，因此三维空间成像技术在生物医学［8-9］、摄影［10］、目标识别［11-13］以及粒子图像测速［14］等领域得到了广泛的应用。

在过去几十年里，学者们付出大量努力突破成像系统的限制，以获得更多维度的光信息。其中，光谱-立体(x，y，z，λ)成像备受关注。大多数光谱-立体成像系统基于扫描或者多次拍照，这会导致拍照时间的延长并因此限制它应用于动态场景。将多个探测器的信息进行融合可以在一次快照获取(x，y，z，λ)信息，然而这样的系统比较笨重并且存在对准误差。本文提出一种快照式光谱-光场成像方法，将聚焦光场成像结构引入到快照式傅里叶变换光谱仪中，在不损失系统横向分辨率的基础上，一次快照就能记录目标场景的(x，y，z，λ)信息。

2 实验仪器与方法

2.1 光路结构设计

快照式光谱光场成像系统的光路示意图如图1所示。来自目标场景的光线由物镜成像至视场光阑，形成第一中间像，然后再经过中继镜头Ⅰ到达微透镜阵列。需要注意的是，此处的视场光阑与单个微透镜形状都为方形。通过调节视场光阑的大小，能够限制微透镜成像子图之间的互相混叠，同时能够抑制杂散光。中继镜头Ⅰ所成的像为虚像（第二中间像），位于微透镜阵列之后。光线经过微透镜阵列后形成一系列的子图像，构成一个子图阵列（Elemental Image Array，EIA），即第三中间像。最后，第三中间像经过检偏器由中继镜头Ⅱ成像至CCD上。此时CCD上的子图阵列的视差记录了目标场景的光场信息(x，y，θ，φ)，并可以重建出其深度信息。

快照式光谱光场成像系统中包含一个快照式傅里叶变换型成像光谱仪（Snapshot Hyperspectral Imaging Fourier Transform，SHIFT），它由微透镜阵列和双折射偏振干涉仪（Birefringent Polarization Interferometer，BPI）组成。其中，BPI由两片偏振片和一个沃拉斯顿棱镜组成。沃拉斯顿棱镜由两片石英光楔胶合而成，其光轴方向如图1（b）中红色双箭头和圆圈所示（彩图见期刊电子版）。两片偏振片的透光轴方向均与沃拉斯顿棱镜的光轴成45°。经过偏振片Ⅰ后，入射光变为线偏振光，其偏振方向与偏振片Ⅰ的透光轴相同。基于沃拉斯顿棱镜的双折射特性，该棱镜将入射光线分成两束。由于入射光线的偏振方向与沃拉斯顿棱镜的光轴成45°，两路光线的强度相同，偏振方向相互垂直。随后，这两束光线经过偏振片Ⅱ后，其偏振方向与沃拉斯顿棱镜的光轴重新成45°。最后，中继镜头Ⅱ将两路光线汇聚并于CCD上发生干涉。两束光线在沃拉斯顿棱镜中的传播过程中，由于寻常光和非寻常光的折射率不同，两路光线之间产生了一定的光程差，该光程差的大小与光线在CCD上汇聚的位置(x，y)有关。如图1（c）所示，由于双折射偏振干涉仪绕z轴旋转了一个很小的角度δ，此时CCD上的光程差可表示为：

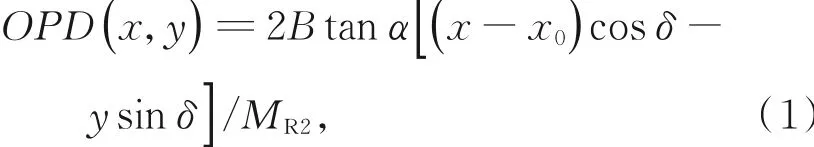
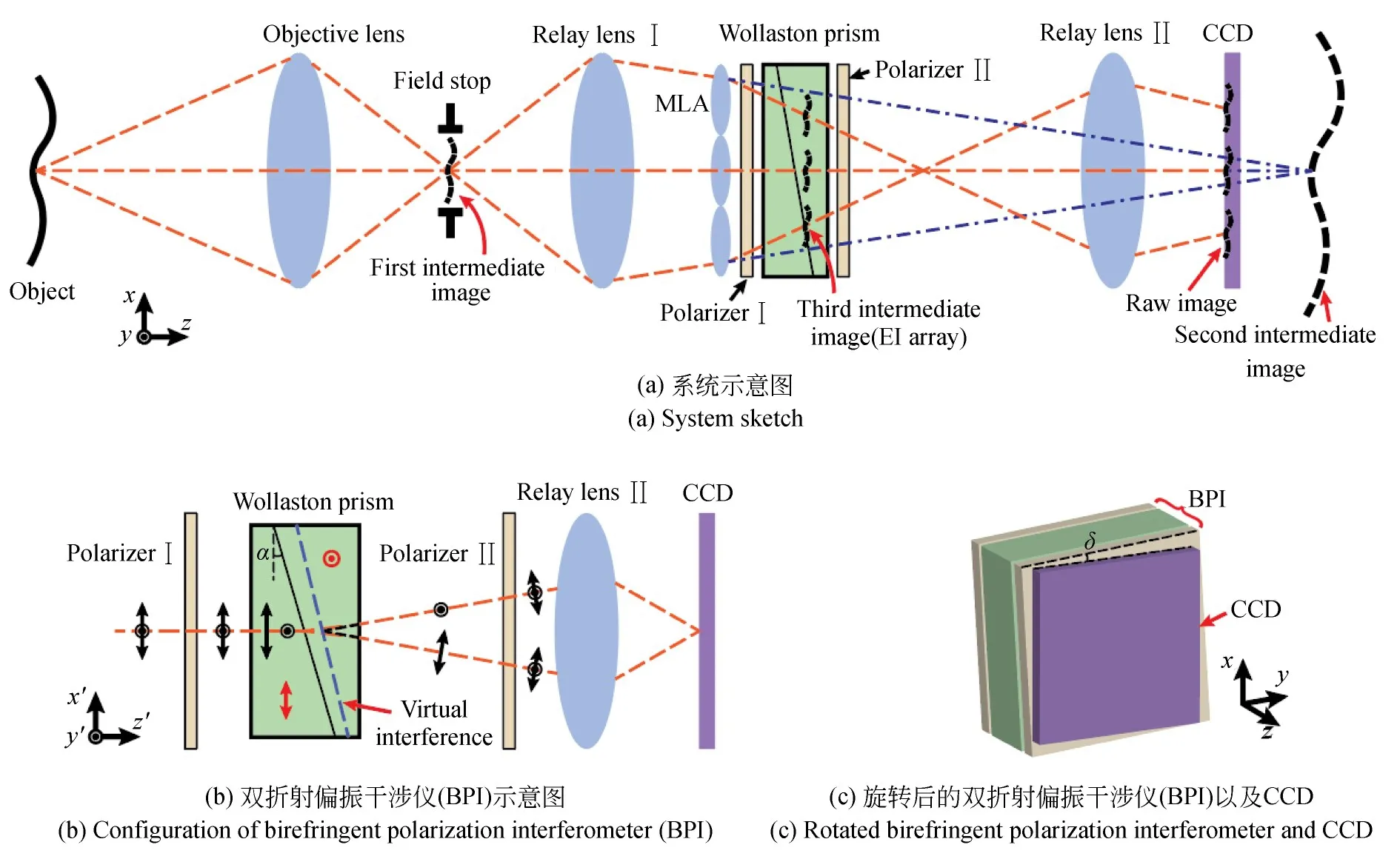
图1 快照式光谱-光场成像系统Fig.1 Snapshot light-field-spectral imaging system

式中：B为石英的双折射率；α为沃拉斯顿棱镜中光楔的角度；MR2为中继镜头Ⅱ的放大倍率；x0为y=0处零光程差点的位置。由于双折射偏振干涉仪绕z轴旋转了一个很小的角度δ，每一个子透镜所带的光程差信息不同，最后呈现在CCD上的每个子图像就带有相应的光程差信息。通过控制δ的角度，令前一行子图像对应点与行间相邻子图像对应点的光程差间距相等，构成等间距采样的子图序列。沿着光程差从小到大的方向，对子图所有坐标点进行遍历，就可以采样得到一个三维干涉数据立方体(x，y，OPD)。经过快速傅里叶变换（Fast Fourier Transform，FFT）后，即可得到目标场景的光谱信息。

2.2 快照式光谱-光场信息重建算法

如图2所示，在轴对称光学系统中，来自物点A的入射光[y′，φ′]T与到达其共轭像点B的出射光[y，φ]T之间的关系可表示为：

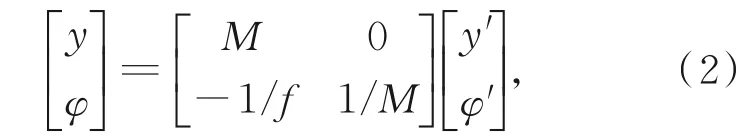
式中：M为光学系统的放大倍率，f为光学系统的焦距。

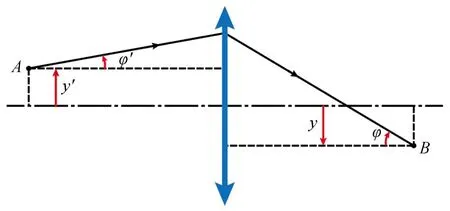
图2 光线在轴对称光学系统中的传播Fig.2 Propagation of light rays in axisymmetric optical system

在快照式光谱-光场成像系统中，由于微透镜阵列的存在，在对各个子图像内的像点进行光线追迹时，需要先将光轴平移至相应的子透镜的中心，然后通过式（2）变换进行光线追迹，最后再将光轴平移回原来的位置。根据上述步骤，对于穿过y轴方向上第v个子透镜的光线，光线到达相应像点的出射光可表示为：

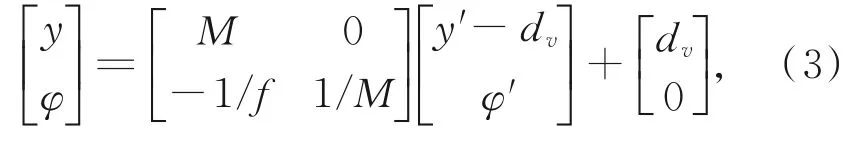
式中dv为光轴到y轴方向上第v个子透镜中心的距离。如2.1节所述，光线经过双折射偏振干涉仪之后会在探测器上产生干涉条纹，而且该条纹的相位由两路光线之间的光程差决定。所以，到达CCD光线的全光函数可表示为：

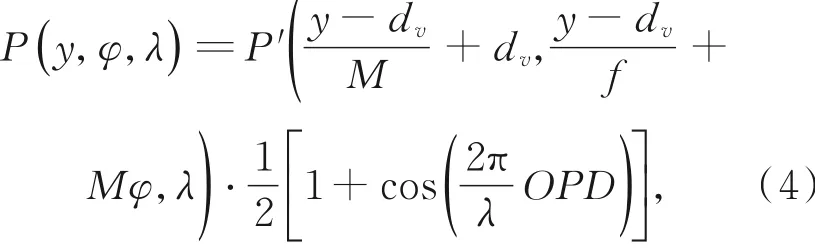
式中P′为来自目标场景光线的全光函数。将式（4）一般化至三维空间并对光线传播角度(θ，φ)以及波长(λ)进行积分，即可得到CCD采集的原始图像，那么有：

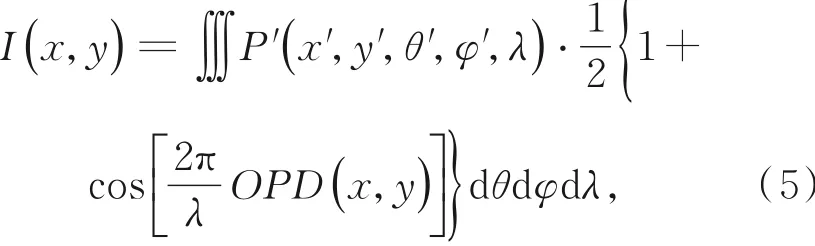
其中x′，y′，θ′，φ′均由式（2）得出。

假设目标物为朗伯体，即来自目标物光线的光谱(λ)独立于其传播角度(θ，φ)。则式（5）可进一步化为：

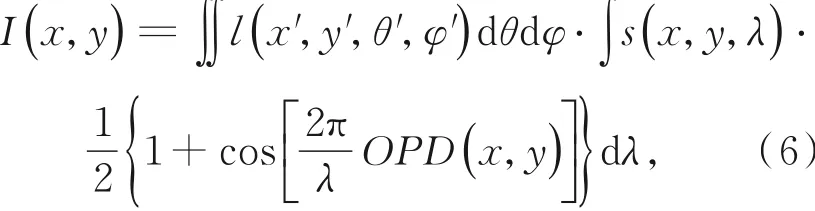
式中：l(x′，y′，θ′，φ′)为目标场景的四维光场立方体；s(x，y，λ)为目标场景的三维光谱立方体。

本文设计的快照式光谱-光场信息重建算法可分为三步：第一步，光场-干涉信息解耦；第二步，从系统记录的光场信息(x，y，θ，φ)中重建目标场景的三维立体信息(x，y，z)；第三步，重建目标场景的三维光谱数据立方体(x，y，λ)。

2.2.1 光场-干涉信息解耦

探测器获得的数据中混叠有光场信息和干涉条纹信息。为了将光场和干涉信息的耦合方式从相乘转换为相加，对式（6）的两边分别取对数，得到：

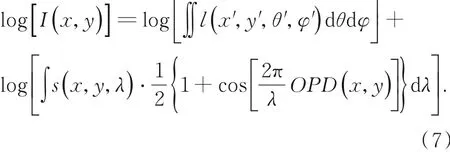
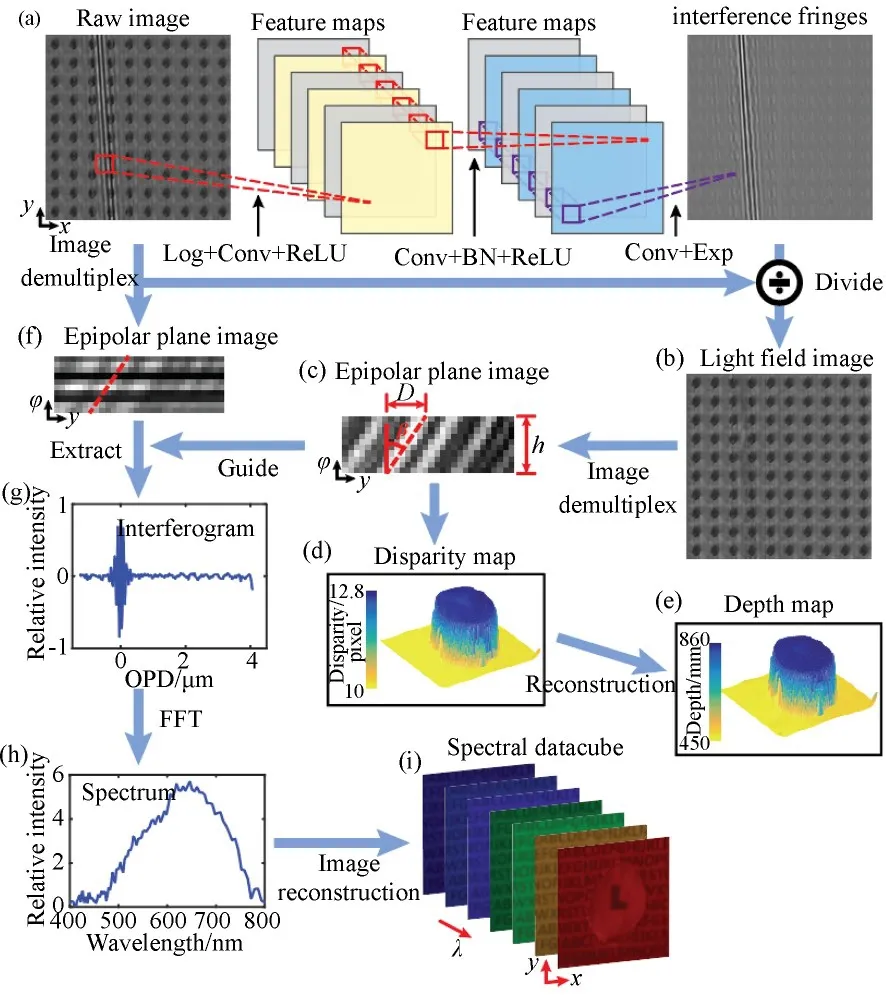
图3 信息重建算法流程。（a）光场-干涉信息解耦卷积神经网络结构；（b）光场图像；（c）从光场图像提取的极平面图像；（d）视差图；（e）深度图；（f）从原始图像提取的极平面图像；（g）单个像素点的干涉序列；（h）单个像素点的光谱；（i）光谱立方体Fig.3 Flowchart of spectral-light-field datacube reconstruction.（a）Framework of the light-field-interferogram decoupling convolutional neural network；（b）Light-field image；（c）Extraction of an epipolar plane image；（d）Disparity map from the light-field image；（e）Depth map；（f）Extraction of an epipolar plane image from the raw image；（g）Interferogram of a single pixel；（h）Spectrum of a single pixel；（i）Spectral datacube

此时，光场-干涉信息解耦问题转化为如何去除图像上叠加的条纹。如图3（a）所示，为实现二者的解混，采用去耦合卷积神经网络（Decoupling Convolutional Neural Network，DC-CNN）进行光场信息和干涉条纹的解耦，从而将光场信息和干涉信息从原始数据中分别提取出来。因为光场图像比条纹复杂得多，这里将条纹设置成学习对象。所设计的DC-CNN架构包含两个中间层和一个输出层。该神经网络的传递方式可以分为以下三个步骤：

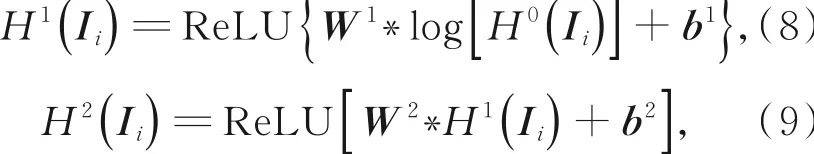
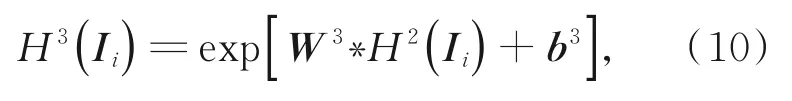
式中：Ii为训练集中第i幅图像；H1(Ii)为第一层隐藏层的输出；H2(Ii)为第二层隐藏层的输出；ReLU（·）为线性整流函数，ReLU（x）=max（0，x）；Wl（l=1，2，3）为DC-CNN第l层的权重参数；bl=（1，2，3）为DC-CNN第l层的偏差参数。

神经网络构架好后，本文采用ICVL数据库来生成用于训练DC-CNN的训练集，并进行训练。如前所述，本系统涉及的干涉条纹是一种规律性很强的图像模式，这会大大降低DC-CNN的训练难度。在训练的过程中，DC-CNN的核函数被定义为：

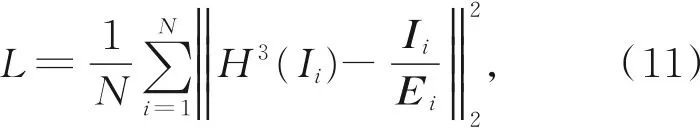
式中：N为训练集中图像的数量；Ii为训练集中第i幅带有干涉条纹的图像；Ei为训练集中第i幅不带干涉条纹的图像。经过训练后，DC-CNN的输出图像即为干涉条纹，将输入图像和输出图像逐个像素点相除，即可得到光场图像。

2.2.2 三维立体信息重建

去除干涉条纹的光场图像，可认为是一个立体相机阵列（微透镜阵列）拍摄目标物而成。该光场图像可以表示为：

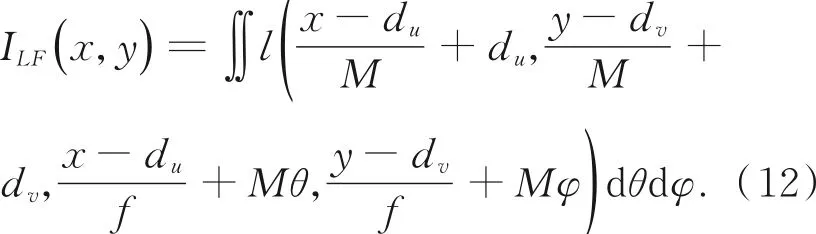
将子图阵列进行重排之后，可得到一个四维的光场数据立方体LF(x，y，m，n)，其中(m，n)分别代表某子图在x轴和y轴的位置坐标，而(x，y)代表该子图的像素坐标。本文采用一种尺度-深度空间变换（Scale-depth Space Transform，SDST）算法［11来重建目标场景的视差图。如图3（c）所示，是该四维数据立方体沿y-n平面的切片，称之为极线平面图。虚线两端是两个不同子图上的同名点（目标场景中同一个点），其连线倾角β即代表该同名点在不同子图中的视差信息，对应该点在目标物空间的深度信息［15］。要得到目标场景的深度信息，首先，计算极线平面图中两同名点的差异为：

其中h为极线平面图沿着n轴方向的宽度。然后遍历所有同名点，就可以得到目标场景中所有点的差异图。最后，经过深度校正得到目标场景的深度图，该深度图可以直观地体现本系统记录得到的目标场景的光场信息。

2.2.3 光谱信息重建

本文直接使用带有干涉条纹的系统采集图来重建目标场景的(x，y，λ)光谱信息。将所有子图按照光程差由小到大的方向重排之后，即可得到一个干涉数据立方体。图4（a）为某个像素点处的干涉序列，横坐标为干涉序列各元素的光程差。对上述干涉序列做傅里叶变换后，经过光谱校正、强度校正等操作后即可得到相应像素点的光谱，光谱密度曲线如图4（b）所示。

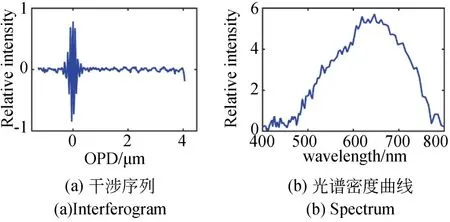
图4 某像素点的干涉序列以及光谱密度曲线Fig.4 Interferogram and spectrum of single pixel

3 结果与讨论

为了验证快照式光谱-光场成像方法的可行性，本文搭建了相应的快照式光谱-光场成像实验系统，并对它在空间、光谱以及时间维度上的表现进行了评价。图5为快照式光谱-光场成像实验系统的实物图。其中，起偏器和检偏器采用大恒光电GCL-050004；物镜采用佳能EF-S 24 mmf/2.8；视场光阑采用大恒光电GCM-5711M；中继镜头Ⅰ采用佳能EF 50 mmf/1.4；微透镜阵列采用Advanced Microoptic Systems GmbH APO-Q-P1000-R5，焦距为10.9 mm，子透镜间距为1 mm；Wollaston棱镜为自主设计外协加工，材料为石英；中继镜头Ⅱ采用大恒光电GCO-232204，其放大倍率为0.44；CCD采用JAI BM-500GE。

图5 快照式光谱-光场成像系统实物Fig.5 Prototype of snapshot spectral-light-field imaging system

3.1 系统的深度重建精度

为了量化分析系统的深度重建精度，采用如图6（a）所示的两个带有字母的白色平板作为目标物，其中距离成像系统较远的平板与系统光轴垂直，另一平板则垂直于xoz平面并与x轴成约45°。图中远端平板上的黄色阴影区域为近端平板遮挡的区域（彩图见期刊电子版）。使用直角规和钢尺测量两平板到成像系统前端的距离，并将该距离作为目标物深度的真值，测量结果如图6（b）所示。图6（c）和6（d）分别为快照式光谱-光场成像系统重建的目标物深度以及该深度的误差。从图中可以看出，由于近端平板对远端平板的遮挡效应，近端平板边缘区域的误差较大。图中其他部分的深度误差均小于10 mm，整图范围内的均方根（Root Mean Square，RMS）误差为7.7 mm。同时，通过设置使系统只具有光场成像的功能，此时其深度重建精度如图6（e）所示。其整图范围内的RMS误差为7.4 mm，与快照式光谱-光场成像系统得到的结果（RMS=7.7 mm）很接近。

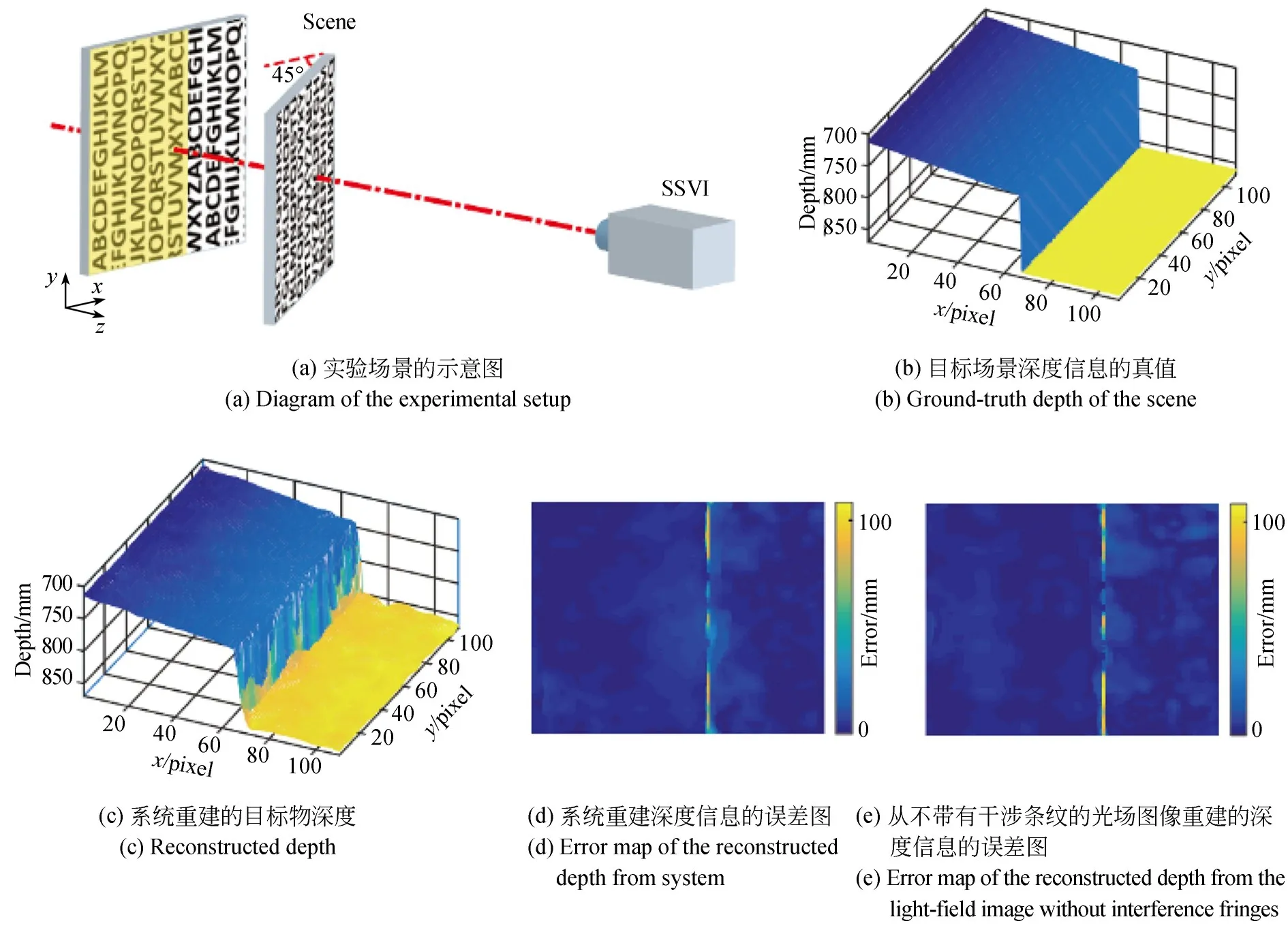
图6 系统获取目标物深度信息的精度Fig.6 Depth accuracy of spectral-light-field imaging system

3.2 系统的光谱分辨力以及光谱重建精度

为了测试快照式光谱-光场成像系统的光谱分辨力，本文使用3个不同颜色的激光器（红色：Melles Griot，25-LHP-925-230，632.8 nm；绿色：Oxxius，532S-100-COL-PP，532 nm；蓝色：Coherent，OBIS 488-60 LS，488 nm）照射一个黑色平板。该平板放置在距离成像系统前端大约900 mm处。图7（a）为系统重建的目标物图像，其中红色、绿色以及蓝色激光光点分别由“Red”、“Green”和“Blue”标识。图7（b）～7（d）分别为系统重建的光谱立方体在3个光点内的光谱曲线，图中的实线为根据实测数据拟合的高斯曲线，内嵌图分别为光谱立方体在632.6，531.6，487.1 nm处的光谱切片。从这些光谱切片可以看出，图像仅在相应的激光光点处有较高的亮度。本文使用激光光谱曲线的半高全宽（Full Width at Half Maximum，FWHM）来表示系统在该波长位置的光谱分辨力。在BPI中，使用一个定制的沃拉斯顿棱镜，其光楔的角度为7.6°。同时，根据式（1）设置x与x0的偏差为1.5 mm，此时系统的最大光程差为28.5μm，其理论光谱分辨力应为350.9 cm-1，它在632.8，532以及488 nm处的理论光谱分辨力分别为14.1，9.9以及8.3 nm。如图7（b）～7（d）所示，系统在632.8，532以及488 nm处的实际光谱分辨力分别为15.4，10.7以及8.4 nm。结果表明，实测分辨力与系统设计的理论分辨力较为接近。

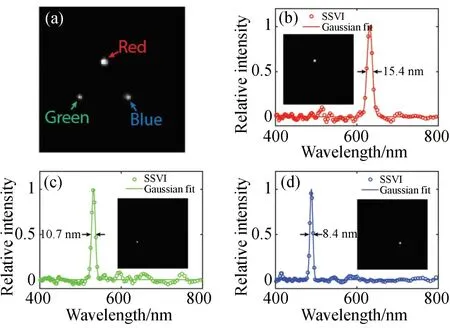
图7 快照式光谱-光场成像系统的光谱分辨力。（a）重建的目标物；（b～d）红色、绿色以及蓝色激光光点处的光谱曲线Fig.7 Spectral resolution of snapshot spectral-light-field imaging system.（a）Reconstructed image；（b-d）Spectra at the red，green，and blue laser points

为了评价快照式光谱-光场成像系统的光谱重建精度，这里使用爱色丽色卡作为系统成像目标物。如图8（a）所示，色卡中的16个色块分别用数字“1～16”标识。本实验中，色卡被放置在距离成像系统约780 mm处，并使用卤素灯作为照明光源。实验使用商业光纤光谱仪（Avantes，AvaSpec-2048）测量各个色块的反射光谱，并作为参考和本系统测得的结果进行比对，比对结果如图8（c）～8（r）所示。从图中可以看出，快照式光谱-光场成像系统重建的光谱曲线与商业光纤光谱仪测得的光谱曲线非常接近。

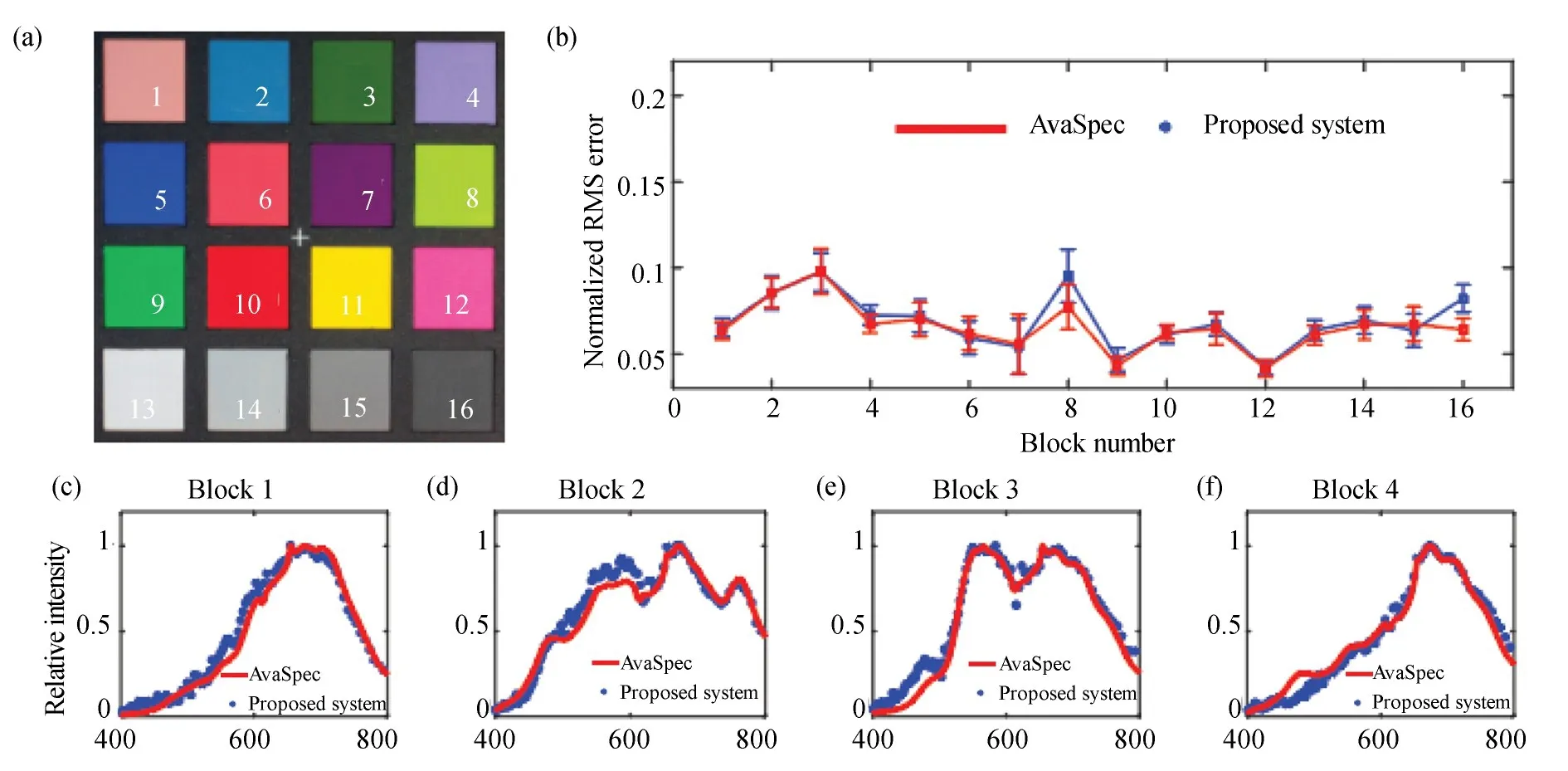
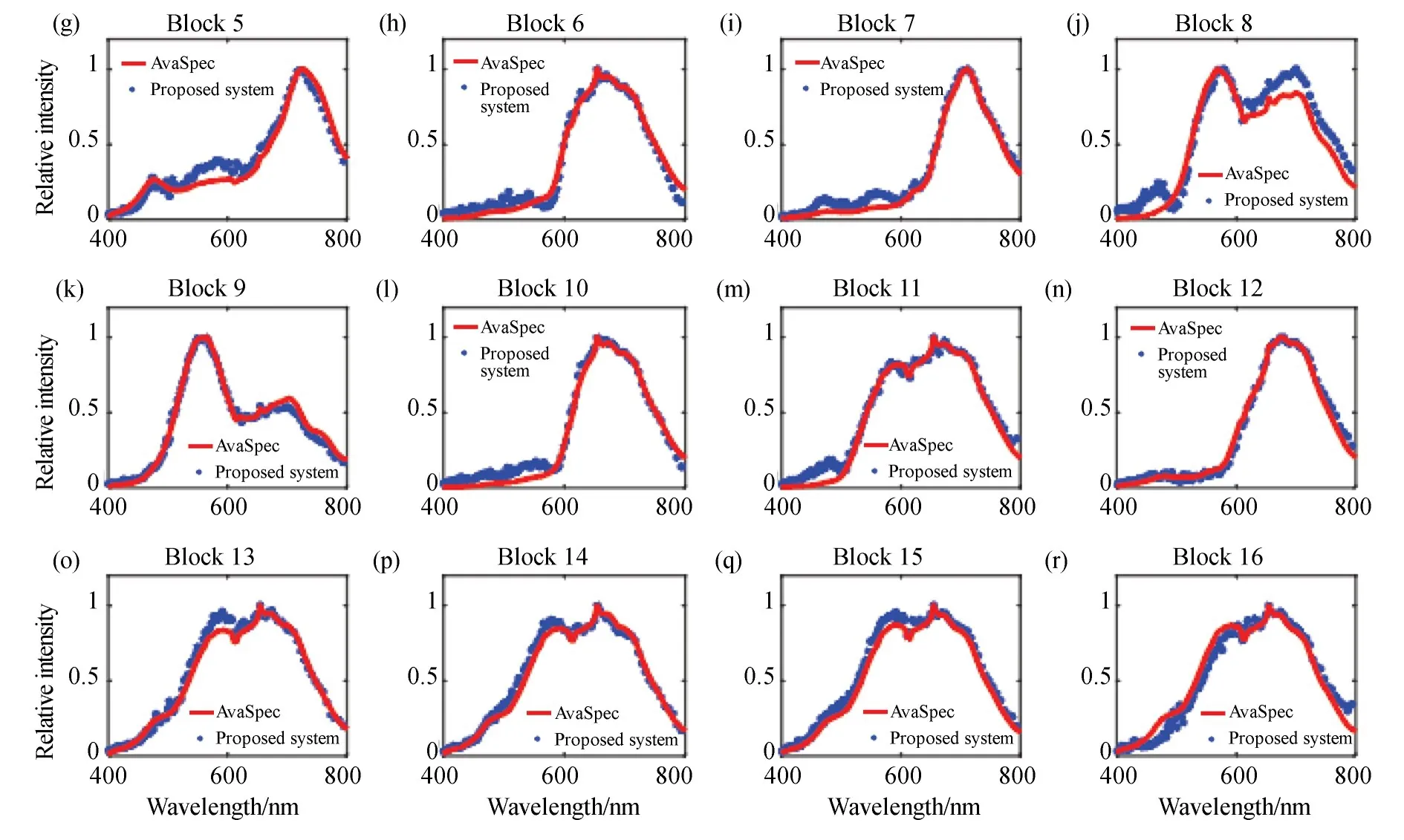
图8 快照式光谱-光场成像系统的光谱重建能力。（a）爱色丽色卡；（b）各个色块内NRMSE的平均值以及标准差；（c）～（r）在不同色块内系统获取的光谱曲线与真值的对比Fig.8 Spectra-reconstruction ability of snapshot spectral-light-field imaging system.（a）Photo of the ColorChecker；（b）Average normalized RMS errors of the reconstructed spectra in color blocks；（c-r）Reconstructed spectra from the SSVI system and the Avantes spectrometer in color blocks

为了量化快照式光谱-光场成像系统重建光谱信息的精度，本实验在每个色块区域内选10×10个像素点，并以商业光纤光谱仪测得的光谱作为真值计算各像素点光谱的归一化均方根误差（Normalized Root Mean Square Error，NRMSE）。图8（b）中的蓝色误差棒表示各个色块内NRMSE的平均值以及标准差（彩图见期刊电子版），所有色块中的平均NRMSE为6.87%。

3.3 分辨力测试实验及系统视场角

本系统采用CCD型号为JAI BM-500GE，像素数为2 058×2 456，同时采用的微透镜阵列包含15×15个子透镜。理论上子透镜对CCD像面进行分割后，最终系统的成像像素数应为137×137。然而，本系统的实际空间分辨力为130×130像素，没有利用CCD的所有像素。这是因为在子图间隔中留有空白区域，以容许微透镜边缘的加工误差。同时，通过本系统对19511951 USAF分辨率板（R3L3S1N，Thorlabs）作为目标物进行成像，来评价系统的横向分辨力，结果如图9所示。由图可以看出，实验结果略低于理论值，其主要原因有二：首先，光学棱镜的像差，尤其是微透镜的数值孔径较小，导致模糊；其次，重建过程中算法误差也会导致成像降质。

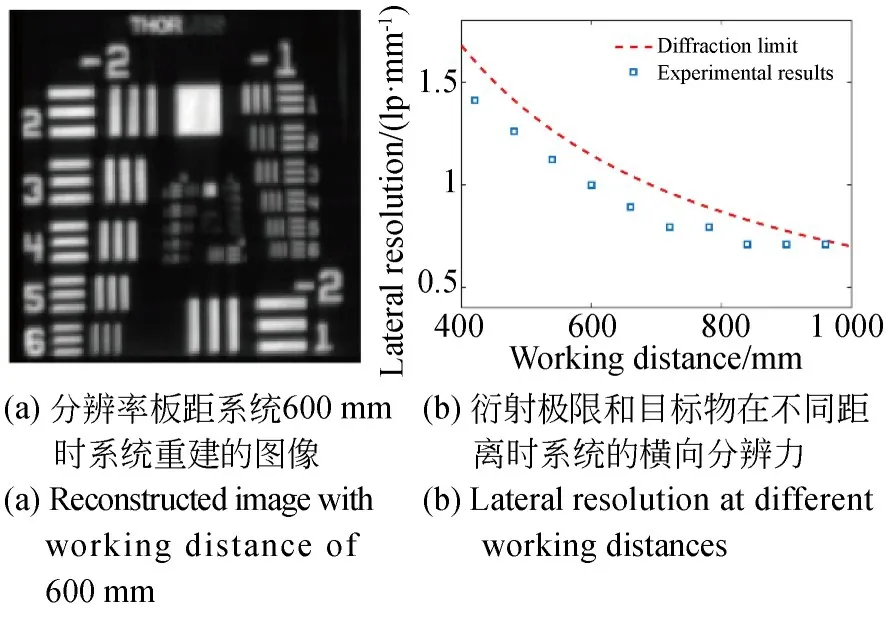
图9 系统的横向分辨力Fig.9 Lateral resolution of proposed system

透镜阵列子透镜间距为1 mm，焦距约为10.9 mm，在CCD被完全利用的情况下，有：

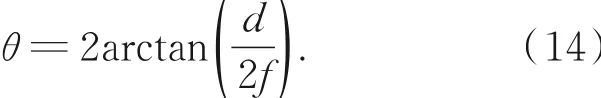
系统的理论视场角为5.25°。而实际测试中，本系统视场角为5.2°，其原因在于子图间隔中留有空白区域，CCD像面并未完全利用。

3.4 光谱-立体视频

为了验证成像系统快速获取目标场景空间以及光谱信息的能力，本文使用如图10（a）所示的动态场景作为成像系统的目标场景。该场景包含一个带有字母的白色平板，以及一个沿光轴方向前后摆动的绿叶。其中，白色平板静止放置在距离成像系统大约850 mm的位置，而绿叶在距离成像系统约420～660 mm内以约2 s为周期前后晃动。图11（c）所示为本实验中使用的绿叶的高清RGB图像，其上粘有一个L形的绿色纸片。

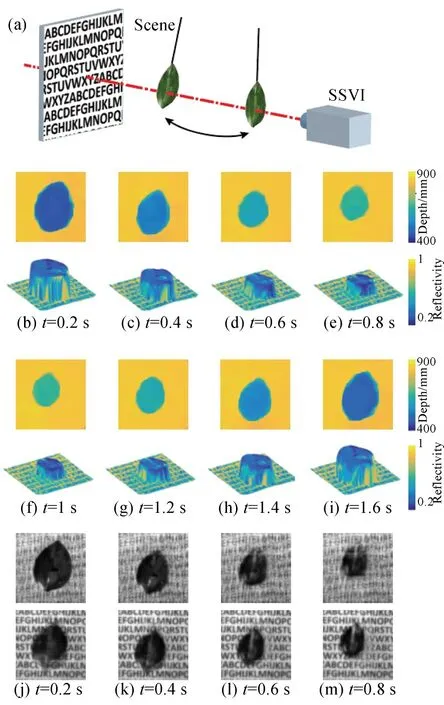
图10 光谱-立体视频。（a）实验场景示意图；（b～i）不同时刻下重建的深度图以及三维图像；（j～m）在不同时刻下成像系统聚焦到450 mm（上行）以及850 mm（下行）处的图像Fig.10 Real-time spectral-volumetric video.（a）Schematic diagram of the experimental setup；（b-i）Reconstructed depth and image frames at different times；（j-m）Samples of image frames reconstructed when the system focuses at 450 mm（upper row）and 850 mm（lower row）

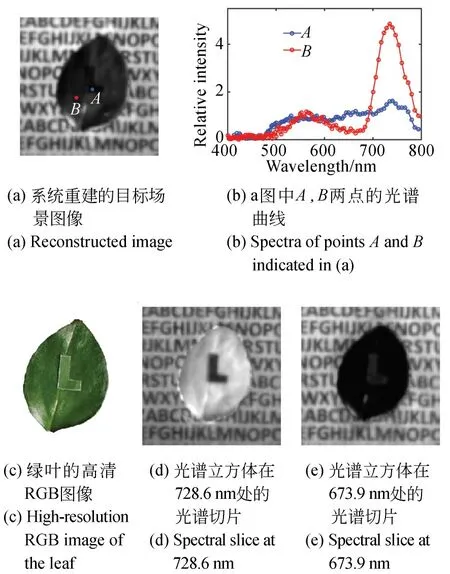
图11 快照式光谱-光场成像系统对同色异谱现象的重建Fig.11 Reconstruction of metamerism by snapshot spetral-light-field imaging system

本实验使用快照式光谱-光场成像实验系统对该目标场景拍摄了一段包含100帧图像、时长约6 s的视频，并使用光谱-深度重建算法对每帧图像进行处理。图10（b）～10（i）分别为系统在不同时刻下重建的深度图以及三维图像。从图中可以看出，快照式光谱-光场成像系统很好地重建了动态目标的空间三维信息。同时，为了验证系统的再聚焦能力，在后期信息重建的过程中分别将系统聚焦在450 mm和850 mm。图10（j）～10（m）分别为系统在不同时刻下聚焦到450 mm（上行）以及850 mm（下行）处的图像。从图中可以清晰地看出，快照式光谱-光场成像系统具有很好的再聚焦能力，展示了本系统记录光线传播角度(θ，φ)的能力。

快照式光谱-光场成像系统能够获取目标场景丰富的光谱信息，因此该系统对色彩的识别能力远优于RGB相机。如图11（a）和11（c）所示，绿色纸片和绿叶的颜色十分接近，所以两者之间的对比度在系统重建的全色图像以及高清的RGB图像中都很低。图11（b）为图11（a）中A，B两点的光谱密度曲线，其中A点和B点分别位于绿色纸片以及绿叶上。从图11（b）可以看出，由于叶绿素在近红外波段的吸收特性，A，B两点的光谱密度曲线之间具有很大的差异。这种现象被称为同色异谱现象，即在某一光照条件下，颜色相同的两种物体具有不同的光谱曲线。此时，人眼以及RGB相机很难将这两种物体区分开来，但由于快照式光谱-光场成像技术具有多维成像能力，在它获取的光谱立方体中取某一特征波段的光谱切片，即可清晰地分辨出同色异谱的物体。图11（d）为系统重建的光谱立方体在728 nm处的光谱切片，从图中可以清晰地分辨出L形纸片的边缘，绿叶区域的亮度明显高于纸片的亮度。与之相反，在图11（e）所示的673.9 nm光谱切片中，绿叶区域的亮度低于纸片的亮度。

4 结 论

本文提出了一种快照式光谱-光场成像方法，使用单个探测器实现了对目标场景光谱-光场信息的快速获取。该方法将聚焦光场成像结构引入到SHIFT光谱仪中，可获取目标场景的空间(x，y，z)、光线传播角度(θ，φ)、光谱(λ)以及时间(t)等七维信息，大大提高了成像系统获取信息的能力。本系统具有多维成像能力，可广泛地应用在生物分析、遥感、机器视觉等领域。

目前，快照式光场光谱成像系统大多依赖于多探测器阵列。它们通过在相机阵列前放置滤波片来获得光谱信息，这限制了系统的光通量，并且光通量与光谱通道数成反比。得益于傅里叶变换成像光谱仪的多重优势，本系统不存在这样的问题。此外，通过使用不同的沃拉斯顿棱镜、微透镜阵列，本系统可以灵活地调整系统的横向分辨率、深度分辨率和光谱分辨率。

由于本系统包含两个偏振片，系统的光通量较低。在未来工作中我们将使用偏振分束器取代系统中的第一个起偏器。穿过偏振分束器的光线进入原系统，偏振分束器反射的光线则接入另一个CCD，从而额外获得目标场景的高分辨率单色图像。该单色高分辨率图像可与原系统的较低横向分辨率图像进行融合，进而提高整个系统的横向分辨力。