大范围平动并联机器人运动学解耦与速度自适应规划

赵新华，刘培昌，赵 磊*，李 彬

（1.天津理工大学天津市先进机电系统设计与智能控制重点实验室，天津300384；2.天津理工大学机电工程国家级实验教学示范中心，天津300384；3.天津理工大学机械工程学院，天津300384）

1 引 言

机器人技术的发展在对提高先进生产竞争力、促进国民经济以及提高战略地位具有重要深远的意义。在机器人应用中，串联机器人具有结构简单和易操作的特点，最早被运用到工业生产领域［1］。但由于仅拥有一条控制链，存在误差积累效应，工作速度相对较低。并联机构具有负载能力强、刚度大和误差不累积等优势，但由于存在多条控制链，关节数量多，导致运动学解耦难度较大［2-4］。从力学角度分析，对于高速并联机构而言，随着机构原动构件转速的提高，惯性负荷会成为激振力的主要组成部分，而且激振力的频率也随之提高［5］。由于连杆机构的各构件的惯性负荷与原动构件转速的平方成正比，故随着机械速度的增加，并联机器人拥有的多个关节的弹性变形以及内部惯性力的耦合作用越加明显，导致轨迹动态跟踪时机器人伴随着不同程度的振动［6-8］。虽然具有多支链、大范围运动工业并联机器人的控制精度相对较低，但其拥有的高速和高负载等明显优势使其仍在工业领域得到广泛应用［9］。

并联机器人具有良好的高速运动特性，但也存在精度和平稳性相对较差的难题。通常采用误差补偿来提高工作精度，选取合理的控制策略实现机器人的高速平稳控制。各种数值算法如改进蚁群算法、遗传算法和神经网络算法被应用到机器人路径规划［10-12］。现阶段，工业机器人在进行实际轨迹跟踪时，在轨迹末端存在一定的惯性速度导致不同程度的冲击晃动，末端控制精度和平稳性较差［13-14］。目前，机器人系统中常用的速度规划算法有梯型速度规划算法和S型速度规划算法。Hu等［15］通过梯型速度规划方法控制机床，验证加速度的不连续变化会引起振动和冲击。史步海等［16-18］提出一种等价梯型的新型S型速度规划算法，算法简单，一定程度上降低机械冲击，但实质上仍属于梯型速度规划。文献［17-18］研究表明：S型速度规划虽然控制算法比梯型控制更为复杂，但速度过渡更为平滑，有效缓解或消除梯型控制存在的因速度突变产生的误差尖峰。然而，在实际应用中，采用S型速度规划算法仍然无法消除或缓解在轨迹末端呈现的冲击效应。

针对3-RRRU大范围平动并联机器人的运动学解耦和速度自适应规划方法展开系统、深入地研究。应用DH法建立机器人的运动学解耦模型，实现了机器人的自动化控制；在S型速度规划策略中引入自适应修正机制，实现了不同轨迹下最大速度的自适应优化，避免了由于速度参数设置不合理导致S型速度曲线的不对称分布，实现了机器人轨迹跟踪过程中速度过渡的平滑性和平稳控制。开展轨迹跟踪实验，验证了所采用速度自适应规划方法的有效性和可行性。

2 并联机器人运动学解耦

2.1 并联机器人结构

图1 是本文所研究的3-RRRU并联机器人，由静平台、动平台和三条支链构成。图2是其对应的结构示意图，静平台固定在上方，动平台则位于下方，且静、动平台均为正三角。三条支链结构相同，每条支链由三个转动副和一个虎克铰连接而成。靠近静平台的均为驱动副，其余为被动副；Aij为第i支链第j的运动副，三个驱动副的轴线均平行于三个相邻被动副的轴线，同时平行于静平台所在平面，又分别垂直于第三个转动副（即第二组被动副）的轴线，三个虎克铰与动平台连接。

2.2 机器人运动学坐标系的建立

以第一条支链为例建立运动学坐标系，O是静平台的几何中心，也是基坐标系O-x0y0z0的原点，OZ0垂直于静平台，设OX0的方向为X轴方向，如图3所示。θij为第i支链第j关节的角位移，旋转轴zi1垂直于轴zi2和zi3，zi3平行于轴zi4；动平台的几何中心为P，其坐标系O-x′0y′0z′0三个坐标轴的方向与静平台坐标系O-x0y0z0的坐标轴方向相同。设机器人支链中各杆件长度为Lij（第i条支链中第j个杆件），R和r分别为静平台和动平台的外接圆半径。

图1 3-RRRU并联机器人Fig.1 3-RRRU parallel robot

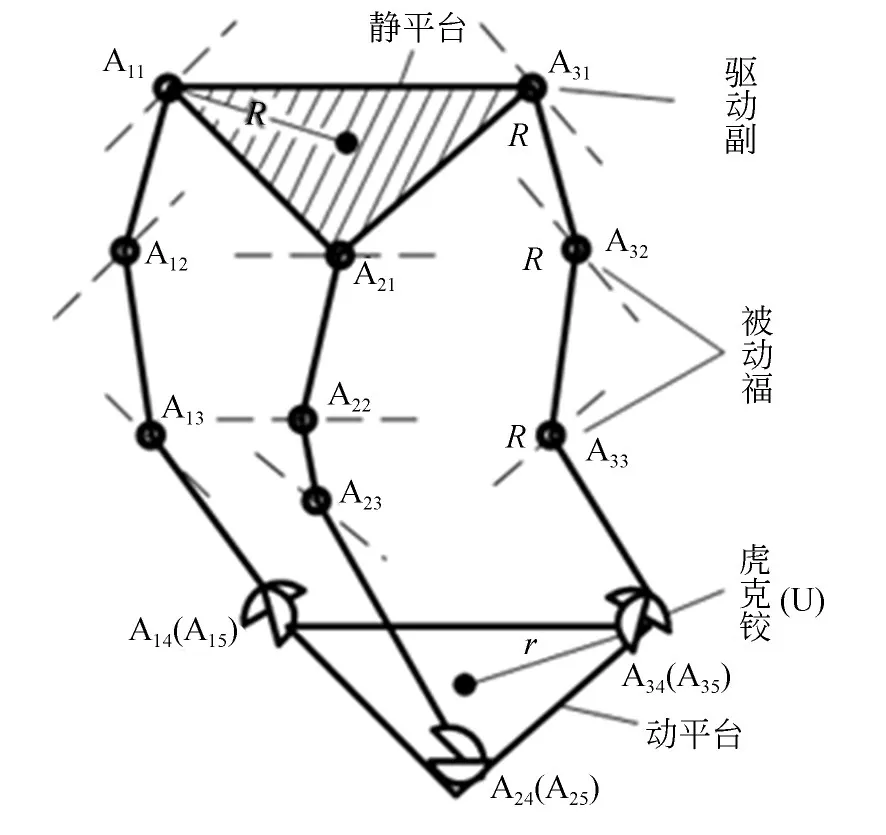
图2 3-RRRU并联机器人结构示意图Fig.2 Structure diagram of 3-RRRU parallel robot

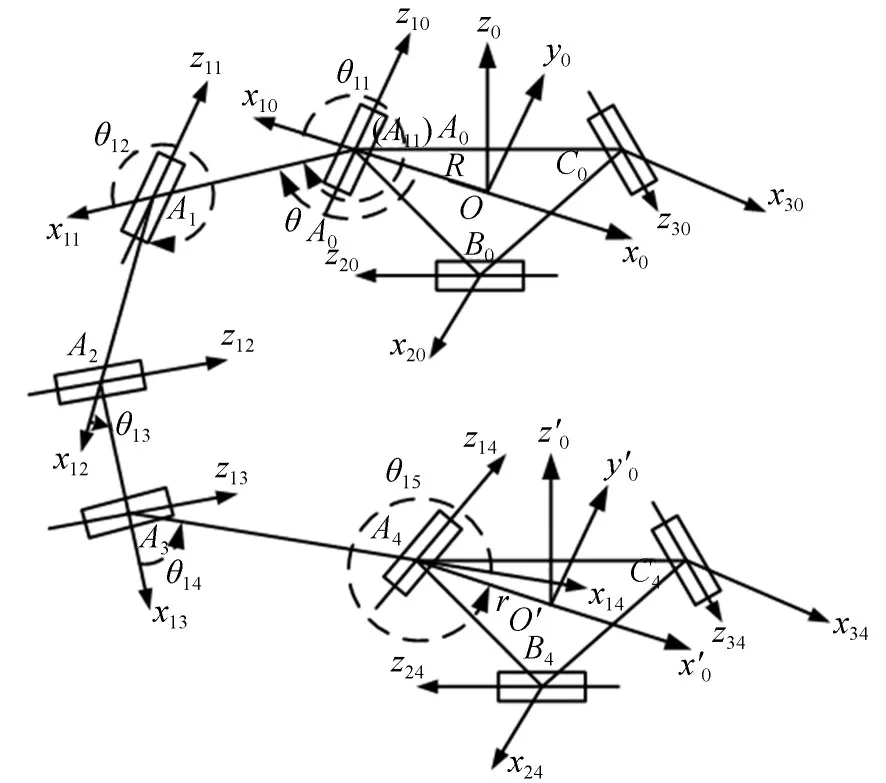
图3 第一支链运动学坐标系Fig.3 Kinematic coordinate system of the first branch chain

2.3 运动学反解

为了实现3-RRRU并联机器人的自动化控制，应用DH法建立其运动学模型。第一支链齐次传递矩阵T可表示为：

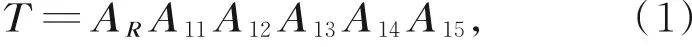
其中：AR为静平台几何中心到第一关节的齐次变换矩阵，Aij为第i支链第j的运动副。

相关矩阵参数如表1所示，对式（1）作如式（2）般变换：

表1 第一支链DH矩阵参数Tab.1 DH matrix parameters of the first chain

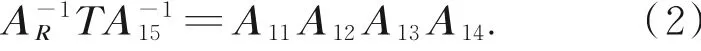
代入矩阵参数可得到第一支链运动学方程如式（3）所示：

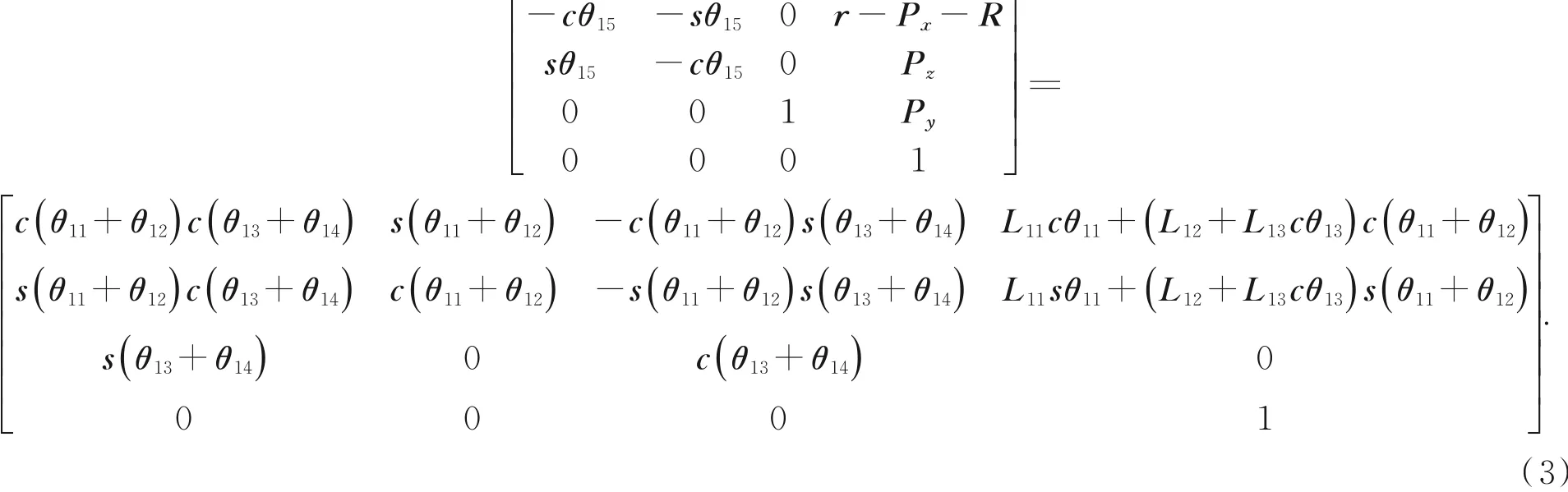
基于机器人结构约束，关节θ13∈[-π/2，π/2]，故由式（3）可得：

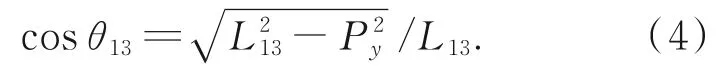
将式（4）代入式（3）矩阵方程进而可求得剩余转角θ11和θ12。同理，将坐标系AR分别旋转60°和120°，亦可完成其他两条支链关节角的计算。结合表2中机器人各构件参数可实现运动学解耦计算，具体计算过程这里不做过多赘述，详见参考文献［19］。

3 速度控制策略优化

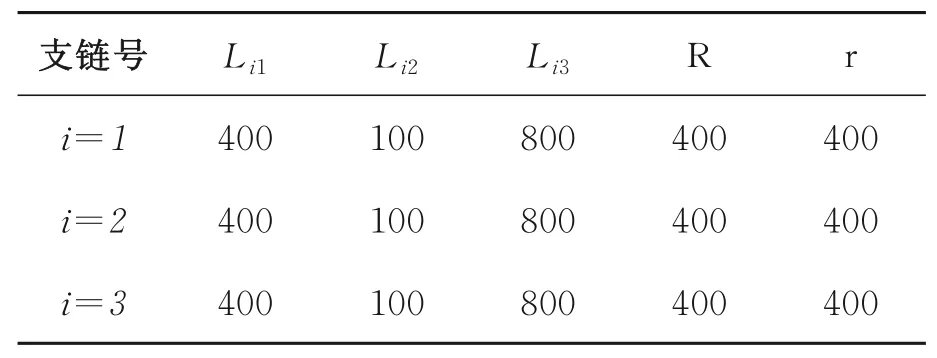
表2 各构件参数Tab.2 Parameters of each component（mm）

3.1 速度自适应修正方法

轨迹规划是机器人运动控制的核心，旨在确定机器人末端执行器在其工作空间的轨迹［19-21］。关于梯型控制原理在文献［16］已详细说明，此处不做赘述，标准S型加减速控制过程共由7个阶段组成，分别为加加速、匀加速、减加速、匀速、加减速、匀减速和减减速，文献［17］给出了位移、速度和加减速过程曲线如图4所示。图4中每个控制阶段的加速度和速度均可通过下式（5）中的加速度和速度函数计算获取。S型控制过程相比梯型复杂很多，设最大速度vm即匀速阶段速度，最大加速度am，加加速度J，轨迹长度为s，s123表示经过加加速阶段s1、匀加速阶段s2、减加速阶段s3达到最大速度时完成的位移；s13表示仅经过加加速段s1和减加速阶段s3达到最大速度时完成的位移，对s123和s13可由式（5）中的速度和加速度函数计算得到。

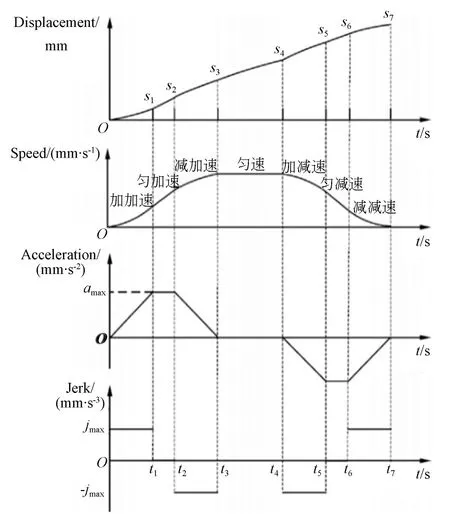
图4 S型加减速控制过程Fig.4 Acceleration and deceleration of S-type control

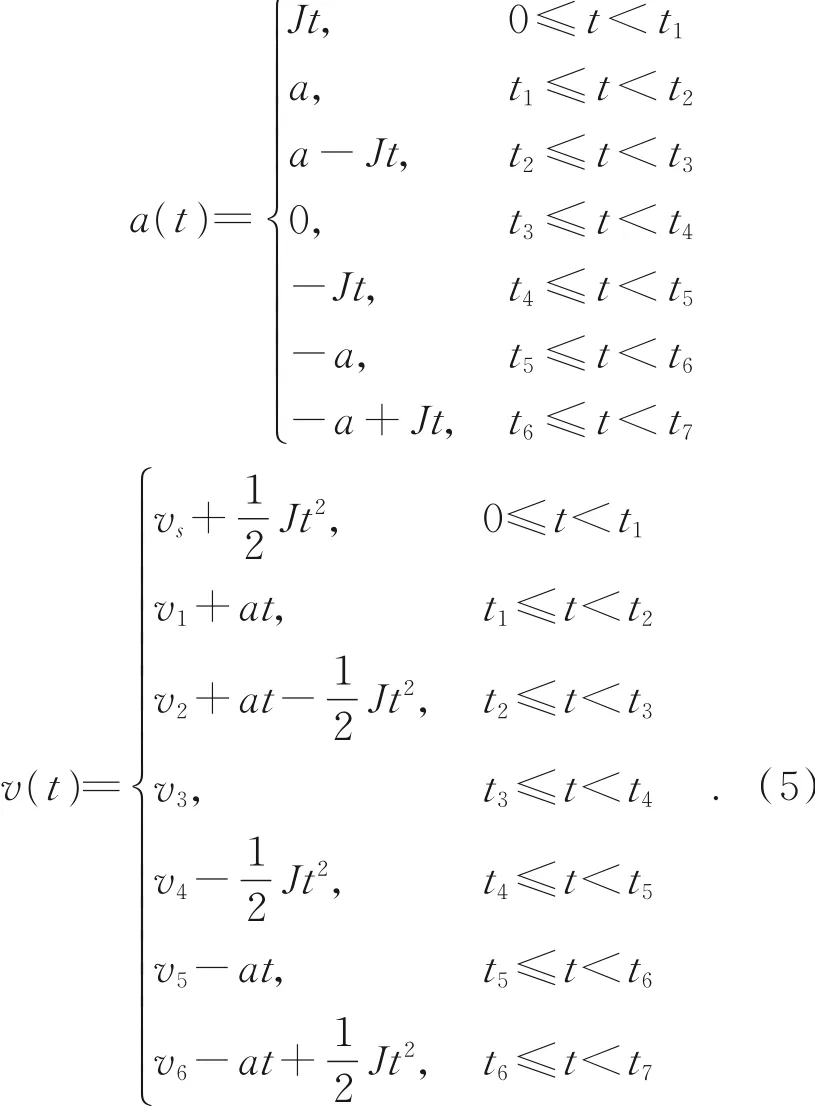
S型速度规划策略中，常采用参数定值控制方式，当轨迹较短时致使预设最大速度值不合理，引起速度曲线呈现不对称分布，此时机器人产生冲击效应即出现明显的晃动。基于上述分析，引入最大速度自适应修正机制如下：

（1）若2s123≤s，仍采用标准S型定值速度控制策略驱动机器人进行预设轨迹的动态跟踪；

（2）当2s13≤s＜2s123，由式（5）可知在给定路径内可以达到最大加速度am，但无法加速到最大速度vm而进入匀速阶段，故S型最大速度vm修正为vnew如下：

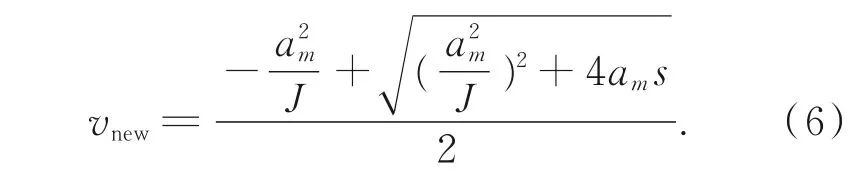
则修正前、后速度曲线如图5所示。

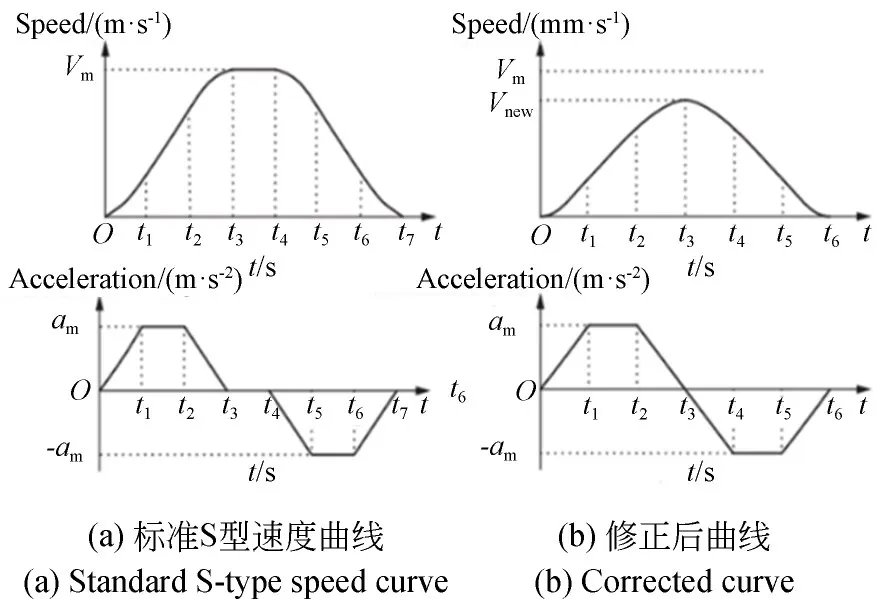
图5 修正前后S型控制速度曲线Fig.5 S-type speed curve before and after correction

基于上述修正机制，速度自适应规划步骤如下：

Step1：在预设路径轨迹上共采样n个位置点，Po(xo，yo，zo)和Pi(xi，yi，zi)分别为机器人初始位置原点和路径轨迹上第i（i=1，2，...，n）点得空间理论坐标，基于运动学反解控制机器人进行轨迹跟踪；

Step2：依据机器人系统设定的最大速度vm，最大加速度am和加加速度J等参数值进行快速判定，是否修正最大速度参数，修正后最大速度为vnew；

Step3：设采样时间为Tc，n为采样点个数，则可获取第i个采样点在t=iTc时刻的速度和加速度，进而可计算出该位置点坐标；

Step4：依据Step2中确定的控制参数应用激光跟踪仪对机器人终端进行动态跟踪，并记录Step1中轨迹上各理论采样位置点所对应的实际空间坐标则第i点跟踪误差为：

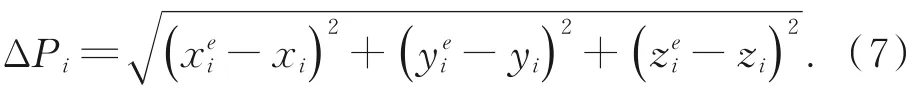
Step5：机器人实际速度ve(t)可由传感器反馈数据获得，则任意时刻t的速度误差Δv(t)=

Step6：采用梯型控制策略进行上述轨迹跟踪，并记录对应采样点数据。

3.2 实验

机器人初始位置为Po(0，0，-0.4)，相关控制参数如表3所示，直线轨迹跟踪在相关文献已做了大量研究，这里不再重复。对xoy平面上两个不同半径的圆轨迹进行动态跟踪实验，圆心均为初始位置点Po，圆半径分别为0.4 m和0.1 m，其对应轨迹长度s分别为2.512 m和1.256 m。

基于预设轨迹通过快速计算和判定，机器人可以加速到最大速度且能够保持速度控制曲线的对称分布。图7是第一条轨迹即半径为0.4 m圆形路径的跟踪情况，基于激光跟踪仪获取的空间采样点位置如图7（a），拟合给出了梯型和常规S型控制策略下机器人实际与理论采样点分布。

图6 3-RRRU并联机器人轨迹跟踪实验Fig.6 Trajectory tracking experiment of 3-RRRU parallel robot

图7 （b）实际跟踪轨迹可以看出：S型控制策略对于曲线轨迹跟踪精度明显优于梯型控制策略。采用梯型控制机器人的跟踪轨迹反映出由于加减速引起的速度突变导致跟踪精度较差且轨迹整体平滑性不如S型速度算法；图8是机器人跟踪误差曲线，从误差曲线可知：S型控制下机器人的位置误差跟踪曲线不存在尖峰值，表明整个路径下机器人运动的平稳性良好，梯型控制由于速度突变产生的最大位置误差达到4.513 mm，是S型控制策略的3倍；此外，从x，y和z方向误差曲线反映机器人在z向误差明显小于x和y方向，S型z向误差分布在-1～1 mm，梯型最大误差约是S型控制策略的2倍；由于并联机器人采用三支链对称设计，存在多支链闭环约束效应，故两种控制策略下x和y向跟踪误差分布也基本一致；若单向误差极大表明机器人结构组装存在很大的误差，需要对支链重新定位和安装。

表3 机器人控制参数Tab.3 Control parameters of robot

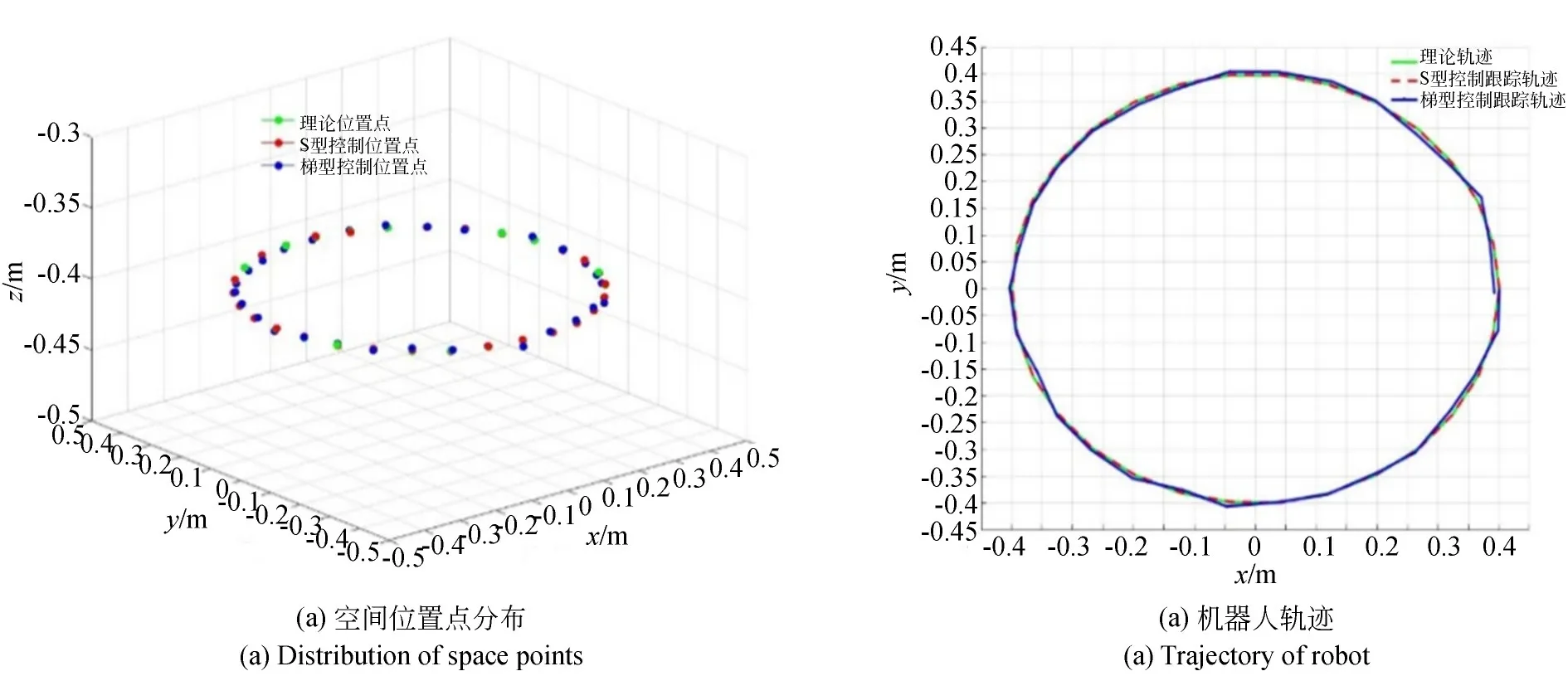
图7 空间位置点分布和轨迹跟踪Fig.7 Distribution of space points and trajectory tracking

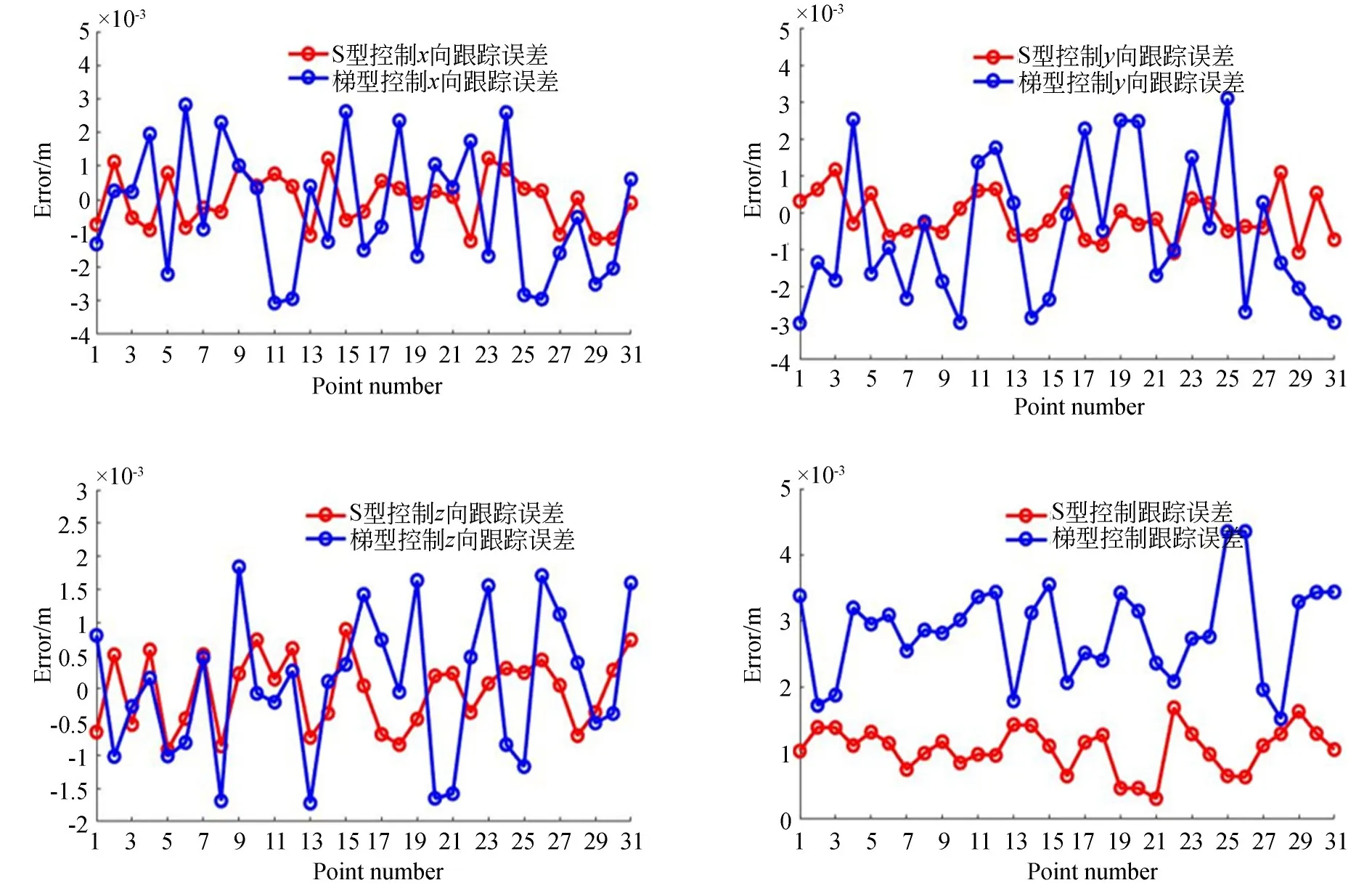
图8 S型和梯型速度规划下的位置跟踪误差Fig.8 Position tracking error under S-type and ladder type velocity planning

图8 表明：S型速度规划策略对轨迹跟踪时具有良好的平稳性，加、减速转变时速度过渡平滑，整体误差分布在0.225～1.615 mm，且没有明显尖峰。

为了测试S型控制策略加入自适应修正机制后控制策略的有效性和可行性，设计第二次路径规划即半径为0.1 m的圆形轨迹，通过修正计算公式，获得优化后的最大速度为1.944 m/s，如表4所示，与预设2 m/s最大速度很接近，故下面测试了最大速度修正前、后机器人的动态跟踪误差。

表4 不同轨迹下速度修正Tab.4 Velocity correction under different trajectories

从图9（a）中实际跟踪位置点分布情况发现，最大速度修正后采样点整体跟踪精度优于修正前，而通过拟合后的跟踪轨迹不难看出，修正前的跟踪轨迹起始点和终点位置误差明显较大；虽然修正后在最大速度位置点与修正前跟踪误差并不明显，但是在轨迹终点机器人速度未减速到零而具有一定的惯性速度，产生冲击效应导致起始点和终点位置偏差很大。

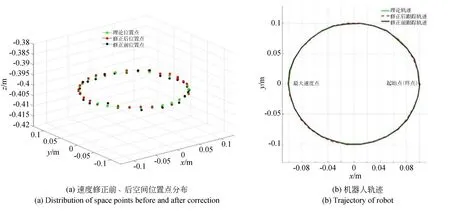
图9 速度修正前后空间位置点分布和轨迹跟踪Fig.9 Distribution of position points and trajectory tracking before and after velocity correction

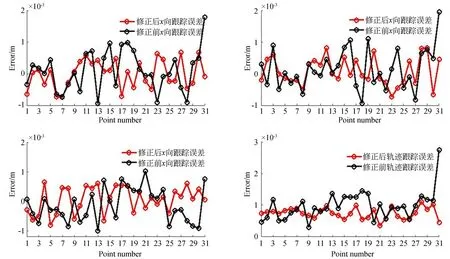
图10 S型控制速度修正前后位置跟踪误差Fig.10 Tracking error before and after speed correction by S-type control

由图10和表5数据可知：速度修正后机器人整体路径的跟踪精度优于修正前，二者误差曲线中误差尖峰很少，表明速度过渡平滑性良好；但修正前机器人在轨迹终点处产生最大误差，表明机器人停止时因具有较大惯性速度而呈现明显的冲击晃动即冲击效应，势必产生误差尖峰，对于航空航天和船舶制造等高精密领域而言是非常危险的；第二次实验预设轨迹是周长未0.628 m的圆，修正前机器人加速到最大速度时其运动距离达到0.330 m，由于S型速度控制曲线是呈对称分布，故在机器人达到终点时，速度并未由减减速阶段平滑过渡为零，产生明显的位置尖峰误差，高达2.676 mm；修正后其位置最大误差仅为1.125 mm，起点和终点位置跟踪误差分别为0.722 mm和0.382 mm，位置相对误差为0.34 mm，表明机器人有效消除了上述尖峰误差。

表5 修正前后位置误差Tab.5 Error before and after correction

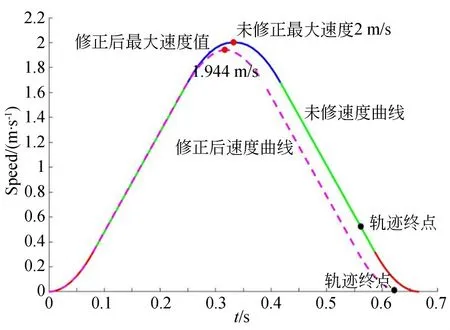
图11 修正前、后速度曲线Fig.11 Velocity curve before and after correction

图11 是机器人最大速度修正后速度控制曲线，机器人控制仍采用预设最大速度值，虽然速度增加到了2 m/s，但是按原有加加速度和加速度进行减速时，在匀减速阶段已到达预设轨迹终点，此时具有一定的惯性速度，停止时势必出现误差尖峰，这与图10所得结论一致；

不难发现，修正后的最大速度为1.944 m/s。虽然略小于预设值2 m/s，但终点位置误差降低了一个数量级，末端控制平稳性大幅提高，有效解决定值控制方式下因速度参数设定不合理而导致机器人末端常出现冲击效应的问题。

4 结 论

S型速度控制策略相比梯型控制具有良好的跟踪精度和平稳性。梯型速度控制下位置跟踪曲线存在多个误差尖峰，其最大误差达到4.513 mm；S型速度规划策略下的位置和速度曲线更为平滑，最大位置误差仅为梯型控制的1/3；

在较短轨迹下，修正前机器人在轨迹末端存在明显的冲击效应，其最大位置误差高达2.676 mm；修正后最大误差为1.125 mm，且机器人终点位置误差仅为0.382 mm，相比修正前降低了一个数量级；

机器人路径变化时，较短轨迹下仍采用常规定值控制，使得预设最大速度值过大进而导致机器人产生末端冲击效应；

引入速度自适应修正机制，有效解决了机器人的冲击效应问题，大幅提高了机器人的动态跟踪精度和平稳性。