傅里叶思想的精髓及其伟大之处

蔡志东

(镇江高等专科学校丹阳师范学院 江苏 镇江 212310)

1 傅里叶生平简介

让·巴普蒂斯·约瑟夫·傅里叶(Baron Jean Baptiste Joseph Fourier，1768年3月21日-1830年5月16日)，法国欧塞尔人，著名数学家、物理学家.

1780年，就读于地方军校.1795年，任巴黎综合工科大学助教，跟随拿破仑军队远征埃及，成为伊泽尔省格伦诺布尔地方长官.1817年，当选法国科学院院士.1822年，担任该院终身秘书，后又任法兰西学院终身秘书和理工科大学校务委员会主席，敕封为男爵.主要贡献是在研究热的传播和热的分析理论，他所创立的一套数学理论，对19世纪的数学和物理学的发展都产生了深远影响.1830年5月16日，在巴黎去世，时年63岁.

2 傅里叶思想的精髓及其伟大之处

2.1 傅里叶思想的精髓

傅里叶的核心思想概括起来有以下两条.

(1)任何一个复杂的函数(或描述事物变化的物理量)在一定的条件下都可以分解为许多简单的正弦或余弦函数的和.具体内容有以下4条.

1)任何一个周期函数(在满足所谓的“狄利克雷或狄里希利条件”下)均可以看成无穷多个(频率跃变的)正(余)弦函数之和.

用物理学的术语来讲：自然界任何一个随时间或空间做周期性变化的事物(物质系统或描述它的物理量)都可以看成无穷多个(频率跃变的)谐振动(即正弦或余弦振动)的叠加.

2)任何一个定义在有限区域上的非周期函数，均可以通过“延拓”的方法把它转化为周期函数，从而仍然可以把它看成无穷多个(频率跃变的)正(余)弦函数的叠加.

用物理学的术语来讲：自然界任何一个局限于一定空间范围内的事物，都可以看成无穷多个(频率跃变的)谐振动的叠加.

3)任何一个(定义在无限区域上的)非周期函数，都可以看成无穷多个频率连续变化的正(余)弦函数的和(积分).

用物理学的术语来讲：自然界任何一个不受限制且表面上看似无规律的事物，都可以看成无穷多个频率连续变化的谐振动的叠加.

4)定义在无限小空间区域(即一个点)上的非周期函数(即所谓的δ函数)，可以看成无穷多个频率连续变化的正(余)弦函数的和(积分).

用物理学的术语来讲：自然界任何一个可以视作点的事物(如质点、点电荷等)都可以看成无穷多个频率连续变化的谐振动的叠加.

(2)世界的本原是一种(谐)振动，静止或不变只是一种表面现象，(周期性)变化才是世界的本原.

2.2 傅里叶的思想和牛顿-莱布尼茨思想的不同之处

傅里叶首先是一个物理学家，他在求解热传导方程时，创立了一套数学理论(核心即傅里叶变换)，解决了一类偏微分方程的定解问题.这一点和牛顿颇为相似.牛顿在解决引力问题时，创立了一种新的数学工具——微积分，在开普勒三定律的基础上导出了引力的基本公式，并进而推广为万有引力定律.但是，他们两个的思维方式是不同的.

牛顿认为，不变是世界的本原.微积分的核心思想就是用无穷多个无限小的直线段来代替曲线(每个直线段的斜率是不变的)，即变化的曲线可以看成许多(斜率)“不变的直线”组合而成.牛顿的绝对时空观和他的微积分的思想也有一些相似之处.尽管时间本身在不停地流逝，但是其量度(时间的长短)却是绝对不变的，而空间长度、物质质量等也是如此.总之，在牛顿的意识中，“不变”占据主导地位，变化只是一种表面现象.

而傅里叶则认为，变化才是世界的本原，即使是表面上看起来不变的水平直线，也可以看成两个相位相差180°的正弦或余弦函数的叠加.傅里叶当初或许仅仅把“变换”当作一种数学方法，没有想到在这“变换”的背后，隐藏着极其深刻的物理思想.

2.3 傅里叶思想的伟大之处

(1)它符合哲学的基本观点

马克思主义哲学的核心可以概括为：一个灵魂(实事求是，一分为二)，二个观点(运动变化的观点和普遍联系的观点)；三大规律(对立统一、量变质变、否定之否定规律).

首先，正弦函数在一个周期内，可以分为上下两个对称的部分(一分为二)；其次，它永远是连续变化的(符合普遍联系，运动变化的观点)；第三，正弦函数由两个既对立又统一的部分组成，当函数值变化到最高或最低点时转而反向变化，符合量变质变规律.由于是周期性变化，自然符合否定之否定规律.

同时，它也符合中国古代的哲学思想.道家学说认为，世间万物均由阴和阳所组成，阴极生阳，阳极生阴，阴阳和合，天人合一.在太极图上，阴阳分别用黑白鱼形图案表示，其变化规律和正弦函数有相似之处.

(2)它符合美学的基本原理

和谐对称是一种美，连续平滑的变化也是一种美.直线的对称性太低(而且没有变化或变化过于简单)，圆的对称性太高(变化过于单调),幂函数比较复杂，对称性也不高，所以都不是很完美.

和谐通常是指两个不同的事物能够完美地组合在一起，形成一个相互依存的整体.直线、圆、幂函数(如n次抛物线)等都不满足这个要求，都不和谐.把两个极端(最低对称性的直线和最高对称性的圆)巧妙地组合起来，比如让半径做圆周运动，半径在水平轴和竖直轴上的投影就分别形成了余弦和正弦函数，这是一种完美的曲线，具有许多独一无二的优点(见下面第三大部分).

(3)它符合物理学的最新观念

现代物理学最伟大的思想有两个：一是真空不空(爱因斯坦首先意识到这一点，认为没有任何场的绝对真空是不存在的，量子场论进一步证实了这一点)；二是认识到，一切粒子乃至一切物体，都不过是真实的(三维空间中的)场振动或十一维时空中的“超弦”振动，这些思想不过是傅里叶思想的进一步发展而已.

(4)它符合数学自身的特点

数学除了具有抽象性之外，还具有逻辑上的严密性和应用上的广泛性.傅里叶变换完全具有这些特点，特别是其应用的广泛性，在众多数学工具中并不多见.

3 正(余)弦函数的独特优点

概括起来，正(余)弦函数有下列9个优点：(1)函数本身的简单性；(2)(函数值的)有限性；(3)对称性；(4)周期性；(5)导数的简单性；(6)连续平滑变化性；(7)三参数性；(8)正交性； (9)不变中的变化性.其中最后3个特点尤为重要，现在简单介绍一下.

正弦函数y=Asin (ωt+φ)中有3个参数：角频率ω，振幅A，相位φ，可以用来表示物理系统的3个特征参量.比如对于一般的系统，我们关注3个最重要的参量：组分的性质、组分的数量或规模、组分的结构(排列组合方式).其他的常用函数一般只有一个或两个参量，很难完整地描述物理系统.

所谓函数的正交性，即两个函数在一个周期内的积分为零，它是矢量正交(或垂直)概念的推广(两个矢量正交，则它们的内积为零).比如函数族

不变中的变化性前面已经有所提及，就是说，即使是表面上看似不变的直线，也可以看成两个相位相反的正(余)弦函数的叠加，运动变化是物质的基本属性.

4 四维协变的傅里叶变换公式

4.1 傅里叶级数的主要公式

若f(x)为一个周期函数，其周期为2l，即f(x+2l)=f(x)，则f(x)可以看成(周期相同的)无穷多个频率跃变的正(余)弦函数的和.

(1)

其中的系数ak,bk相当于“函数矢量”f(x)的无穷多个分量，正(余)弦函数则相当于无穷多个“基矢”.文献[1]给出了系数的公式

(2)

(3)

定义在有限区域上的非周期函数，可以通过“延拓”转化为周期函数，然后用类似的方法展开为傅里叶级数.为简单起见，有时傅里叶级数也可用复数表示

(4)

(5)

4.2 傅里叶变换(积分)的主要公式

如果f(x)是定义在无限区域上的非周期函数，根据文献[1]～[3]可知，可以把它展开为无穷多个频率连续变化的正弦或余弦函数之和(积分)，此即所谓的傅里叶变换，其复数形式为

(6)

(7)

当然也可以把式(6)、式(7)写成对称形式

(8)

(9)

还可以从一维推广到三维“空间”，即将

ωx→k·r=kx+ky+kz

同时做下列置换

可得三维空间的傅里叶变换公式

(10)

(11)

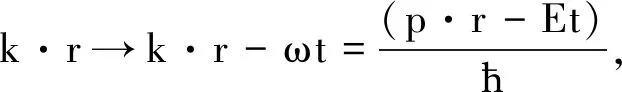
(12)

(13)

式(12)和式(13)即为量子力学中最常用的变换公式[4].

4.3 四维协变的傅里叶变换公式

式(12)、式(13)不具有洛伦兹协变性，因为它只对三维坐标或三维动量进行变换，没有对时间和能量进行变换.下面导出洛伦兹协变的傅里叶变换公式.令四维动量矢量[5]

四维坐标矢量

(xμ)=(x1,x2,x3,x4)=(x,y,z,ict)=(r,ict)

则有

(14)

上式右边采用了爱因斯坦求和约定(相同指标表示求和).作下列替换

式(12)、式(13)化为

(15)

(16)

式(15)、式(16)即为洛伦兹协变的傅里叶变换公式，具有完美的对称性和简洁性，非常优美.它是“四维(闵可夫斯基)坐标空间”和“四维动量空间”之间的变换.也就是说，一个空间的函数可以通过“无穷多个基本函数”变换到另一个空间的函数，反之亦然.

与此相似，定义在无限小区域(一个点上)的非周期函数，也可以通过傅里叶变换，展开为无穷多个正弦或余弦函数的和(积分).

5 傅里叶变换的应用领域

由于复数形式的一维傅里叶变换中，基本函数为eiωx，其导数或微分后仍然是这个函数(前面多一个或几个常数)，从而使线性微分方程的求解可以转化为常系数的代数方程的求解，这在数学和物理上都非常有用.此外，著名的卷积定理指出：傅里叶变换可以化复杂的卷积运算为简单的乘积运算，从而提供了计算卷积的一种简单手段.离散形式的傅里叶变换可以利用数字计算机快速算出.由于这些性质以及本文第三大部分所讲的9个特点，使傅里叶变换在物理学、数论、组合数学、信号处理、概率、统计、密码学、声学、光学等领域都有着广泛的应用.

从军用到民用，从基础科学(如量子力学)到应用科学(如计算机、通信、激光等).

从周期到非周期函数，从粒子到场，均可以应用傅里叶变换来解决许多实际问题.其应用领域之广，除了微积分和微分方程之外，很少有其他工具可以和它相媲美.

很多专家说，傅里叶变换就是从时域变到频域，这是一种非常肤浅的认识，傅里叶变换所蕴含的思想之深刻，远远超越了绝大多数人的想象.希望本文能有助于读者加深对傅里叶变换的认识.