信息传播影响下基于进化蜂群算法的应急车辆路径优化设计
于明亮, 刘 帅, 浦东平
(1.上海理工大学 公共实验中心,上海 200093;2.上海师范大学 信息与机电工程学院,上海 200234)
应急物资作为突发事件防控的重要保障,其配送的合理性和送达的及时性不仅关系着民众的生命安全和生活保障,而且影响着地区的经济发展和社会稳定。而实现有效应急物流配送的前提是需要准确预测灾区的物资需求,且该需求数量与受影响人数密切相关。在当前这个移动互联技术高速发展的时代,突发事件的影响范围不再仅由自然因素、环境因素和经济因素等决定,个体间的信息传播也在一定程度上影响着突发事件的发展态势。因此,为了更加准确地预测应急物资需求且更加合理地设计车辆配送方案,在构建应急物流优化模型时应该加以考虑灾情传播和信息传播之间的关联。
目前关于应急物流的研究一方面集中在应急物流网络设计[1-3],如刘明等[4]综合考虑了人口流动和密度特征,设计了基于服务水平的应急物流网络优化模型,反映了物资需求和救援成本之间的偏好侧重。蒋杰辉等[5]设计了基于Holling-II 函数的SIP(susceptible,infecteive,protester)疾病扩散模型,结合智能水滴算法对以时间短和成本低为目标的应急物流问题进行研究。邓烨等[6]针对可靠度、满意度、经济度及鲁棒度等多种要求解决了不确定环境下的应急物资车辆的路径优化问题。另一方面,国内外学者也重点关注于应急物资动态分配[7-9],如Büyüktahtakin 等[10]同时考虑了传染病的空间传播和后勤问题,设计了一种物流混合整数规划模型来确定物资分配的最佳数量、时间和位置。Dasaklis 等[11]基于反应行动延迟和反应能力有限等现实情况采用线性规划模型制定了大规模疫苗接种活动所需的物资分配方案。王妍妍等[12]通过区间数、三角模糊数及延迟系数等反映应急物资供给与需求关系之间的非确定性,并在最大程度上衡量延迟时间与系统损失来制定出多周期的应急物资分配方案。通过对现有文献进行分析可以发现,绝大部分的研究都忽略了信息传播对于应急物资需求和分配的影响。
本文研究的应急物流问题本质上可以转化为多目标下的路径优化问题,与其他求解多目标优化问题的智能算法所不同的是,人工蜂群算法(artificial bee colony algorithm,ABC)的设计思路是模仿蜂群寻蜜的过程[13],这种通过划分多种群进行并行寻优的方法更加贴近物资配送的车辆路径优化过程[14]。在人工蜂群算法被提出之初,其主要被应用在解决具有连续性的优化问题中,而近年来也逐步被应用于包括路径规划问题在内的离散问题求解中[15]。如张架鹏等[16]运用差分进化算法和模拟退火算法的思想设计了一种改进的离散型蜂群算法,并将其应用在求解同类机调度问题中。Li 等[17]将改进的离散人工蜂群算法应用于具有维修活动的多目标柔性作业车间调度问题中,与传统人工蜂群算法所不同的是,其所提出的算法能够生成具有多样性的初始种群并能给出唯一解。
目前将人工蜂群算法与路径优化问题相结合的研究仍处于初始阶段。如Pamučar 等[18]将自适应模糊神经网络与人工蜂群算法相结合来求解多目标危险品运输的城市路线规划问题,从而有效降低了成本和风险。段渊等[19]提出了新的离散型蜂群算法来解决经典的旅行商问题,通过离散的交叉算子和单/多步2-opt 算子来确定新的蜜源。郑健等[20]引入了精英保护策略和动态侦察蜂机制对传统人工蜂群算法进行了优化,并将该算法用于解决基于方向标志的离散型路径规划问题。
在已有研究的基础上,本文首先建立了一个基于SIS-UAU 双层扩散网络的预测模型用以得出各个灾区的应急物资需求量。其次针对多目标下的应急物流问题设计了一种新的离散人工蜂群算法(进化蜂群算法)。该算法通过有效利用适应度值、历史进化程度、交叉算子及变异算子等操作来保障迭代效率和避免陷入局部最优。最后通过一个应急物资配送算例,表明了本文所提出的需求预测模型和改进离散算法的有效性,并在综合考虑时间短和成本低的前提下得到了最佳应急物资配送路线。本文相较于其他应急物流和蜂群算法的研究主要有以下3 个方面的不同:第一,结合双层扩散网络着重考虑了实际中信息传播和个人行为的影响因素,从而能更加准确预测灾区应急物资的需求量。第二,进化蜂群算法加入了交叉算子和变异算子,实现了对优秀信息的保留和传递,加速了蜜源向最优解的进化。第三,进化蜂群算法综合考虑了蜜源的适应度值和历史进化程度,并基于此将蜂群进行重新划分,从而充分挖掘了蜂群价值并显著优化了计算效果。
1 应急物流问题的描述和模型
1.1 基于双层扩散网络的需求预测模型
在分析灾情扩散时不仅考虑了突发事件对于个体的影响程度,而且考虑了通过预警信息传播能够使人们获取灾情相关信息并降低影响程度,从而建立了基于信息传播和个体行为的双层扩散网络。
双层扩散网络中的上层为事件层,采用susceptible-infected-susceptible(SIS)传染病模型来表示[21]。在SIS 模型中,个体分别处于易感染(susceptible,简称S)和感染(infected,简称I)两种状态。针对本文的突发事件情况,在灾情发生前所有个体都处于不受影响的状态,则无影响者可用SIS 模型中的S 表示;而在灾情发生后部分个体受到了影响,则受影响者可用SIS 模型中的I 表示。随着灾情的恢复,受影响者会重新变为无影响者。
双层扩散网络中的下层为信息层,采用unawareaware-unaware(UAU)信息传播模型来表示[22]。在UAU 模型中,个体分别处于没有信息(unaware,简称U)和有信息(aware,简称A)两种状态。针对本文的突发事件情况,在灾情发生前所有个体都处于无信息状态,则无信息者可用UAU 模型中的U 表示;在灾情扩散时有部分个体获得了信息且另一部分个体依然没有获得信息,则有信息者可用UAU 模型中的A 表示。同时,由于信息会随着灾情的发展而不断更迭,所以,灾情前期的有信息者在灾情后期也可能变为无信息者。
通过双层扩散网络可以预测出各个灾区某一时间段的受影响者数量,从而计算出不同灾区在该时间段所需要配送的物资量。将处于SIS-UAU双层网络中的个体分成SU(没有信息的无影响者)、SA(有信息的无影响者)、IA(有信息的受影响者)3 种状态,且个体一旦被影响则其肯定会获得信息,所以,不存在没有信息的无影响者。图1为双层扩散网络示意图。虽然事件层和信息层的个体总数相同,但是,各层内个体之间的联系却不同。每个个体都有各自的行为状态,分别由活跃状态和不活跃状态表示。白色圆圈表示活跃状态,黑色圆圈表示不活跃状态。

图1 双层扩散网络Fig.1 Two-layer spread network
在双层扩散网络中,事件层度为l且信息层度为k的个体数量表示为Nlk。3 种状态在t时段按照度分类的个体数量分别表示为S Ulk(t),S Alk(t)和IAlk(t)。 同时,令分别表示该时段3 种状态占个体总数的密度值,并且成立。
因此,3 种状态SU,SA 和IA 的个体状态改变概率可以分别表示为
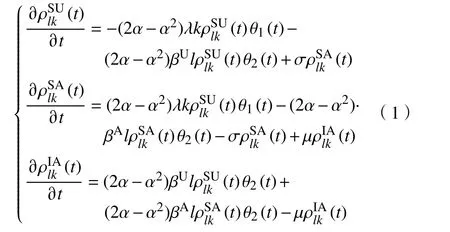
式中: α为个体处于活跃状态的概率; λ为无影响者处于活跃状态时获取信息的概率; σ为接触到信息的无影响者忽视信息的概率; μ为接触到信息的受影响者转变成有信息的无影响者的概率; βU为没有获取到信息的个体受到影响的概率; βA为获取到信息的个体受到影响的概率, βA=(1-φ)βU;φ为获取信息的概率; θ1(t)为 个体i任意一条连边连接到具有信息个体的概率; θ2(t)为 个体i任意一条连边连接到已受影响个体的概率。
然后,基于双层扩散网络来预测各个灾区在t时段的受影响者总数IAlk(t),从而计算该灾区所需的物资量Pr如式(2)所示。

式中: ω0为每位受影响者在一个时间段内所需的物资量; ε为物资量不足的置信水平;为第i个区域在t时段经过物资配送延迟时间tj后的受影响者总数;qi为 在t+tj时 刻第i个灾区对物资的需求预测总量。
1.2 多目标应急物流模型
多目标应急物流所要解决的问题是如何合理安排若干辆相同型号的车辆分别从配送中心出发对各个灾区进行物资配送。本文的目标是找到一条最优的路线规划,在满足各个灾区物资量的基础上使车辆的行驶路程最短且所需的配送时间最少。利用基于双层扩散网络的需求预测模型得出各个灾区在t时段的物资需求量qi,并在此基础上对模型集合、参数和决策变量进行设置。
在对模型集合的设置中,V′为灾区i,j的集合,V′={1,2,···,N},i,j∈V′。V为顶点集,V={0,1,2,···,N},其中,0 代表应急物资的配送中心。Q为应急物资需求量qi的集合,qi∈Q。M为车型m的集合,m∈M。T为时间t的集合,t∈T。E为灾区之间距离d的集合,di j∈E。
在对模型参数的设置中,di j表示灾区i到灾区j之间的距离,dmax表 示灾区i到灾区j距离的阈值,即距离若超过dmax, 则不安排物资配送。Vm为配送车辆m的行驶速度,tm为 车辆m在单位距离内所需的运输时间,tij为 灾区i到灾区j所需的运输时间,gm为 车辆m单位距离的可变成本,cmj为车辆m出配送中心的单位增加成本,Fm为 车辆m的最大装载量,u为应急物资的单位质量,qi(t)为在t时段灾区i对应的应急物资的需求量。
在对决策变量的设置中,xmij(t) 为 0-1 决策变量,表示在t时段是否安排车辆m从灾区i运送应急物资到灾区j。ym j(t)为 0-1 决策变量,表示在t时段灾区j是否由车辆m来运送应急物资。

建立多目标应急物流模型。式(5)的目标为所需配送的时间T最短,式(6)的目标为车辆运输成本C最低。
对于以上目标函数,为应急物资运输时间设定一个阈值tmin,若应急物资能够在规定的时间内运送到灾区,则时间成本为零,否则时间成本增加。同时,引入时间成本系数 β来表示超过阈值tmin的延期罚函数系数,其测算方式为未满足物资需求量延续一个单位时段对目标函数的增加量。时间成本系数 β 可根据实际车辆路径问题的紧急程度人为确定,通常情况下该系数的单位为元/h。将时间看作成本的一部分,把时间成本和运输成本相加获得总成本,从而将多目标函数转换为单目标函数。最终的应急物流配送模型为

式(7)的约束条件为

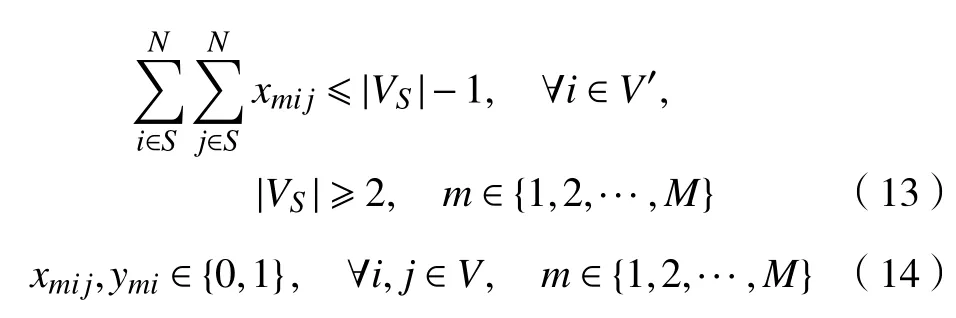
上述约束条件中,式(8)中,tj表 示车辆m到达灾区j的时刻,tc表示车辆m到达灾区c的时刻。式(9)表示配送车辆所能覆盖的最大范围约束,若有效距离超过了阈值,则灾区i到灾区j不安排车辆配送。式(10)表示每条配送路线上各灾区的需求总量不能大于所分配车辆的最大负载Fm。式(11)表示共有M辆车来完成应急物资配送任务,且每个灾区仅分配一辆车进行运送。式(12)~(14)保证了车辆路径规划能够形成可行回路,其中,S表示顶点集的任一子集合,VS为 集合S的顶点个数。
2 进化蜂群算法
2.1 人工蜂群算法
人工蜂群算法是一种仿照群体智能的全局优化算法,通过模仿现实中蜜蜂采蜜的过程,该算法将人工蜂群分为了引领蜂(employed bees)、跟随蜂(onlookers)和探索蜂(scouts),从而使得3 类蜜蜂能够在寻找最优蜜源的过程中各司其职。在人工蜂群算法求解过程中,首先引领蜂基于已有信息来寻找蜜源,并将找到的蜜源信息告诉跟随蜂;然后跟随蜂依照获得的信息按照一定概率来挑选候选蜜源,将该候选蜜源与之前的蜜源进行比较,保留更优的蜜源;最后当某个蜜源经过有限次循环后没有更新时,则与该蜜源相关的蜜蜂转变为探索蜂来继续找寻潜在的新蜜源。
当采用人工蜂群算法来解决优化问题时,每个蜜源都意味着优化问题中的一个解,且蜜源的花蜜数量意味着解的适应度值,而在反复迭代过程中发现的最佳蜜源就是该问题的最优解。设定解的搜索空间为D维空间。由于在人工蜂群算法中引领蜂或跟随蜂的数量与蜜源的数量相同,因此,引领蜂、跟随蜂和蜜源的数量均为SN,且引领蜂和蜜源存在对应关系。引领蜂和跟随蜂根据式(15)在搜索空间中生成候选蜜源。
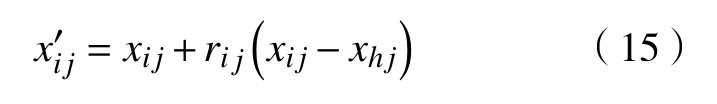
式中:表示新发现的候选蜜源,i和j是随机产生,i∈{1,2,···,S N},j∈{1,2,···,D};ri j为均匀分布在[-1,1]上的随机数,用来规范候选蜜源的选择范围。
跟随蜂依据概率pi来选择蜜源,如式(16)所示,以适应度值来表示各蜜源的花蜜数量,且适应度值越大的蜜源,越有机会被选中。
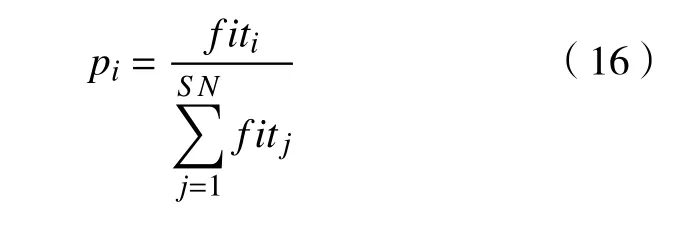
式中,fiti表示第i个蜜源xi的适应度值。
若引领蜂和跟随蜂经过有限次循环后没有再次更新某个之前被选中的蜜源,那么,该蜜源将会被放弃,与该蜜源相关的蜜蜂将会变为探索蜂,并根据式(17)寻找新的蜜源。

式中: rand(0,1)是 区间[0,1]上的随机数;为第j维的最小值和最大值。
2.2 进化蜂群算法
本文所设计的进化蜂群算法主要用于解决离散优化问题,如多目标应急物流问题。传统的人工蜂群算法是采用实数编码,进化蜂群算法通过自然数编码来解决路径规划等离散问题。本文算法有效融合了适应度值和迭代进化程度来判断蜜源的好坏,同时利用交叉算子和变异算子组成的进化操作来合理选择候选蜜源。
现有文献中对于人工蜂群的改进方法主要以当前迭代过程中的适应度值来作为判断蜜源优劣程度的标准,而直接放弃了适应度值暂时排名靠后的蜜源,造成了已知优秀蜜源搜索次数过多而候选蜜源附近难以被充分挖掘,从而忽视了蜜源的潜在价值并降低了蜂群的搜寻活力。为了能够充分利用蜜源信息,应该给搜索空间中进化程度较大的蜜源更多的搜索机会。同时,为了避免计算量的骤增,本文仅考虑进化程度较大的蜜源且限制了搜索次数,从而增加了发现最优蜜源的可能性。
对于蜜源优秀度的衡量,不能仅考虑某次迭代过程中的适应度值,而是应该综合考虑近期蜜源的平均历史进化程度,蜜源的迭代进化程度定义为

在式(18)中,各个蜜源的编号由i表示,整个蜂群的迭代次数由t表示,此次蜜源进化结束时刻由Nd表示。用来衡量蜜源进化程度的时间间隔由Nb表示,在算法运算过程中需要保留各蜜源的每次迭代进化程度。
同时,将交叉算子和变异算子进行融合,从而生成候选蜜源,通过交换蜜源之间优秀的位置信息以突破蜂群内的固定状态并脱离局部最优,实现蜜源的进化以达到更高水平的平衡状态。在进化蜂群算法的运算迭代中,保留各蜜源的适应度值与蜜源进化程度,将进化程度排名靠前的蜜源运用交叉算子和变异算子来进化生成子代蜜源。将得到的子代蜜源与原来的蜜源的适应度值进行对比,若比原来的蜜源优秀,则进行替换。
交叉算子:按照交叉概率pc, 采用PMX(部分匹配交叉)法则进行交叉操作。在2 个父代蜜源中随机截取一段,并在这2 个父代蜜源所选段内进行连续交换,通过这些交换从而得到子代蜜源。例如,首先选取一个优秀蜜源段为[5,2,6,7,4,0,1,3,8,9] 和一个邻近蜜源段 [5,0,6,3,8,4,7,2,9,1]。其次随机产生2 个随机数满足 0 ≤k1≤k2≤k,k为蜜源的长度,如k1=3 和k2=7 作为截取蜜源段的起始位置和结束位置,得到 [5,2,6|7,4,0,1|3,8,9] 和[5,0,6|3,8,4,7|2,9,1]。接着再将截取到的2 个片段进行位置交换,得到 [5,2,6|3,8,4,7|3,8,9] 和[5,0,6|7,4,0,1|2,9,1]。最后解决编码重复的冲突问题,对于[5,2,6|3,8,4,7|3,8,9]中原蜜源的3 和8 刚好与交叉过来的片段 |3,8,4,7|出现了重复,根据父代蜜源的 初 始 映 射 关 系 7 ↔3、 4 ↔8、 0 ↔4、 1 ↔7可 以得到子代蜜源段为 [ 5,2,6|3,8,4,7|1,0,9]。
变异算子:根据变异概率pm随机生成一个变异点jm(m=1,2,···,h+m),将子代蜜源循环左移jm个位置。例如,经过交叉操作后的子代蜜源段为[5,2,6,3,8,4,7,1,0,9],jm=3,经变异操作后生成的最终蜜源段为 [ 3,8,4,7,1,0,9,5,2,6]。
2.3 进化蜂群算法求解过程
通过构建的基于双层扩散网络的需求预测模型并利用Python 软件得到每个灾区对应的物资需求。通过无向图G=(V,E,q)来描述多个灾区的配送车辆规划问题。V={0,1,2,···,N}表示顶点集,0 指代应急物资的配送中心,其余数值指代各个等待配送的灾区。为边集,各个灾区之间的距离为di j。qi∈Q,i={1,2,···,N}代表各灾区所对应的物资需求。将应急物流优化问题下的多目标模型转变成单目标模型,并通过进化蜂群算法进行求解。
解决应急车辆路径问题等同于要找出一条长为h+m的最佳蜜源,每一个蜜源被编码成一个解{0,x11,x12,···,x1n,0,x21,x22,···,x2v,···,0,xm1,xm2,···,xmw},表示第一辆车从物资配送中心出发,途径灾区点x11,x12,···,x1n返回到始发地。以此类推,第m辆车从物资配送中心出发,途径灾区点xm1,xm2,···,xmw返回到始发地。本文采用的自然数编码方式相较于传统的实数编码方式,不仅减小了运算搜索范围,而且加快了迭代收敛速度。
进化蜂群算法求解多目标应急物流优化问题的步骤如下:
步骤1初始化变量,包括通过双层扩散网络下的需求预测模型来得到灾区数量N和每个灾区所需要的物资量qi∈Q,i={1,2,···,N},配送中心和各灾区之间的距离di, 车辆m单位距离的可变成本gm,车辆m出配送中心的单位增加成本cmj,车辆m的行驶速度Vm,车辆m最大载重量Fm。蜂群的规模S,放弃条件L,最大迭代次数Mc。
步骤2初始化进化蜂群,整个蜂群包含相等数量的引领蜂和跟随蜂,且每个引领蜂与一个蜜源相关,所以,蜂群大小S的一半等同于初始蜜源个数FN,即FN=S/2。且所有蜜源初始化进化程度为0,搜索次数为0,用于衡量蜜源进化程度的时间间隔Nb=1。
步骤3计算所有蜜源的适应度值fiti。根据式(7)得到目标函数值Zi,则适应度值函数为fiti=1/Zi。 若Zi对应的解不可行,则赋予该解一个很大的整数R,从而在算法迭代中能够被淘汰。计算所有蜜源的进化程度(第一次迭代时的进化程度等于适应度值),选出进化程度排名前FN/3的优秀蜜源GS并记录下最优蜜源BS。
步骤4引领蜂带领跟随蜂到优秀蜜源GSi附近随机搜索另外的蜜源NSi,且依据轮盘赌原则分配探索蜂的数量。然后采用交叉算子和变异算子来完成进化操作,产生GSi和NSi的 一个子代蜜源SSi。
步骤5在完成进化后,更新所有优秀蜜源GS的搜索次数hi,t=hi,t-1+Ni,t,其中,hi,t表示在编号为i的优秀蜜源GSi在 第t代对应的历史搜索总次数,Ni,t表 示编号为i的优秀蜜源GSi在 第t代对应的搜索次数。每一次进化操作后将产生FN/3个子代蜜源SS,并将这些子代蜜源的搜索次数赋值为0。
步骤6计算所有优秀蜜源、剩余蜜源和子代蜜源的适应度值和迭代进化程度,此时共有4FN/3个蜜源。根据进化程度对所有蜜源进行排名,选择排名前的蜜源成为新一代的优秀蜜源进行进化操作。删除排名最后FN/3个的蜜源,同时更新最优蜜源BS。
步骤7若hi,t>L,即第i个蜜源的搜索次数已经大于限制次数,则删除第i个蜜源。那么,这个蜜源所对应的引领蜂变为探索蜂,并在下一次迭代中,按照排名次序增加一个优秀蜜源的数量,使探索蜂对这个新增加的优秀蜜源进行进化操作。
步骤8迭代总次数n=n+1, 判断n>Mc是否成立,或者判断是否达到了对应的精度要求,若成立则可以结束运算,输出所有迭代过程中的最优蜜源;否则返回步骤3 继续迭代。
3 算例分析
假定最初在某地区发生了突发事件,从而产生了部分受影响者。经过一段时间后,与该地区相邻的其他区域的个体也受到了一定程度的影响。基于双层扩散网络的需求预测模型的基本参数如表1 所示[5,22]。可以将时间段分为无影响阶段、影响扩散阶段、影响控制阶段和影响消亡阶段。
根据这些参数可以计算得到4 个阶段中有信息的无影响者(SA)、有信息的受影响者(IA)和没有信息的无影响者(SU)数量的变化趋势,如图2所示。可以看出,影响程度从最初发生突发事件至到达顶峰总共经历了10 天,从影响扩散阶段的第3 天出现有信息的受影响者,且该人数在影响控制阶段的第4 天到达峰值。

图2 影响变化趋势Fig.2 Influence change trend
设定一共有30 个灾区,每个灾区的位置坐标如表2 所示,数据来源于VRP 国际标准测试数据库(类型:A,节点:31,车辆数:3)。已知每个灾区已经受到影响的时间和物资配送延迟时间,可根据式(1)和式(2)分别得到各个灾区对于物资的需求量。其中,第3 个灾区和第10 个灾区的物资需求量最大均为159,且物资需求量在100 以上的灾区达到了14 个,可见突发事件正处于紧急状态。

表2 灾区基本参数Tab.2 Basic parameters of emergency areas
设物资配送中的坐标(X,Y)为(61, 59),其编号为第14,该中心总共有3 辆额定载重量为1 200 kg的汽车,配送车辆平均行驶速度为60 km/h,车辆出行一次的固定成本g=200 元,单位运输成本c=2 元/km,时间成本系数 β=100 元/h。
进化蜂群算法求解多目标应急物流问题的参数设置为跟随蜂50、探索蜂10 和引领蜂3,测试函数的维数为1 000,迭代次数为1 600 次。车辆运输总路径长度的收敛情况如图3 所示,从图3 中可以发现,进化蜂群算法在前期收敛过程中的稳定性要优于人工蜂群算法,且后期的收敛效果要好于人工蜂群算法。这是因为进化蜂群算法在求解多目标物资配送路径的过程中对部分进化程度较大的蜜源给予了更多的选择机会,且在蜜源进化过程中能够使优秀的蜜源信息得以保留,从而在求解末期可以有效地避免局部最优并提高求解效率。
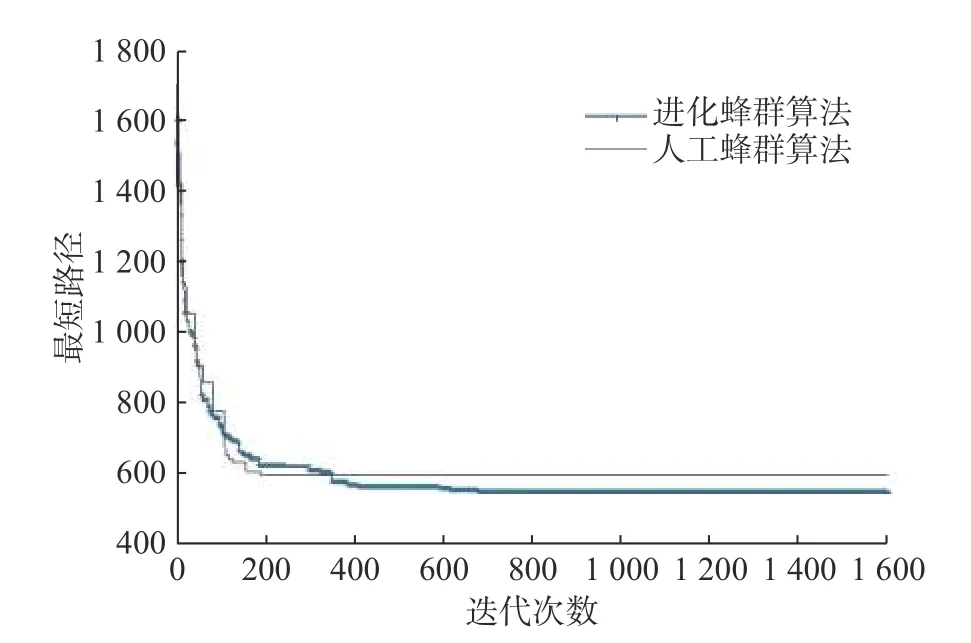
图3 算法收敛效果Fig.3 Algorithm convergence effect
当累计迭代次数达到671 次时,可得多目标应急物流的最优路径里程为596.129 km。此时,3 辆汽车的行驶路径和物资配送方案分别如图4 和表3 所示,可以看出,3 辆汽车将原本分散且杂乱无章的灾区划分为3 个部分。其中,A3 路线所经过的灾区数量最多且行驶距离最长,A2 路线所经过的物资需求量超过100 的灾区最多但行驶距离最短,A1 路线所经过灾区的物资需求量最少,但是,行驶距离则接近于A3 路线。综上,3 条线路在载重量、行驶距离和运输成本方面均实现了合理分配,使得应急物资能够在最短的时间内以最高效的方法送达各个灾区。

图4 车辆行驶路径Fig.4 Vehicle paths

表3 应急物资调配方案Tab.3 Emergency material distribution plan
4 结束语
应急物资的合理分配和及时送达对于突发事件的防控而言至关重要,本文以准确性、合理性、时间短和成本低为目标研究了多个灾区的物资需求和车辆配送问题。首先,考虑到移动互联时代下信息传播和个体行为对于灾情扩散的影响,构建了基于SIS-UAU 双层扩散网络的需求预测模型,以保证应急物资分配的合理性和准确性。其次,设计了一种改进的离散蜂群算法来有效优化车辆的运输路径,不仅利用交叉算子和变异算子使蜜源在进化过程中的优秀信息得以保留,而且依据适应度值和历史进化程度为优秀蜜源提供了更多的搜索机会,从而充分挖掘了蜂群价值并有效提升了迭代效率。最后,通过算例表明了进化蜂群算法在解决离散路径选择问题时要优于传统的人工蜂群算法,且在车辆载重量和行驶距离等方面均实现了合理分配,能够在最短时间内以最低成本完成应急物资运送。由于现实中的物资配送是一个重要且复杂的问题,因此,未来将从以下两个方面继续进行研究:一方面是研究多层多维度的应急物资配送问题;另一方面是研究多配送中心、多种运输方式下的应急物资配送问题。

