核心素养视角下的数学课堂教学探讨

摘 要：本文通过对新教材“4.2.1指数函数的概念”教学过程的解读，探讨核心素养视角下的数学课堂教学过程，分析如何在课堂中落实数学核心素养。

关键词：核心素养;数学课堂;指数函数概念

《普通高中數学课程标准》（2017年版2020年修订）明确指出，高中数学课程标准修订的重点是落实数学学科核心素养，这对数学教师提出了新的要求。通过校本教研、学习讨论、教学实验、展示交流等途径，数学教师要深刻认识数学学科核心素养的育人价值。

以下是笔者执教的新教材内容高一数学必修一第四章第二节第一课时“4.2.1指数函数的概念”教学实践流程。

一、 问题与情境

问题1 随着中国经济高速增长，人民生活水平不断提高，旅游成了越来越多家庭的重要生活方式。由于旅游人数不断增加，A，B两地景区自2001年起采取了不同的应对措施，A地提高了景区门票价格，而B地则取消了景区门票。

比较两地景区游客人次的变化情况，你发现了怎样的变化规律？

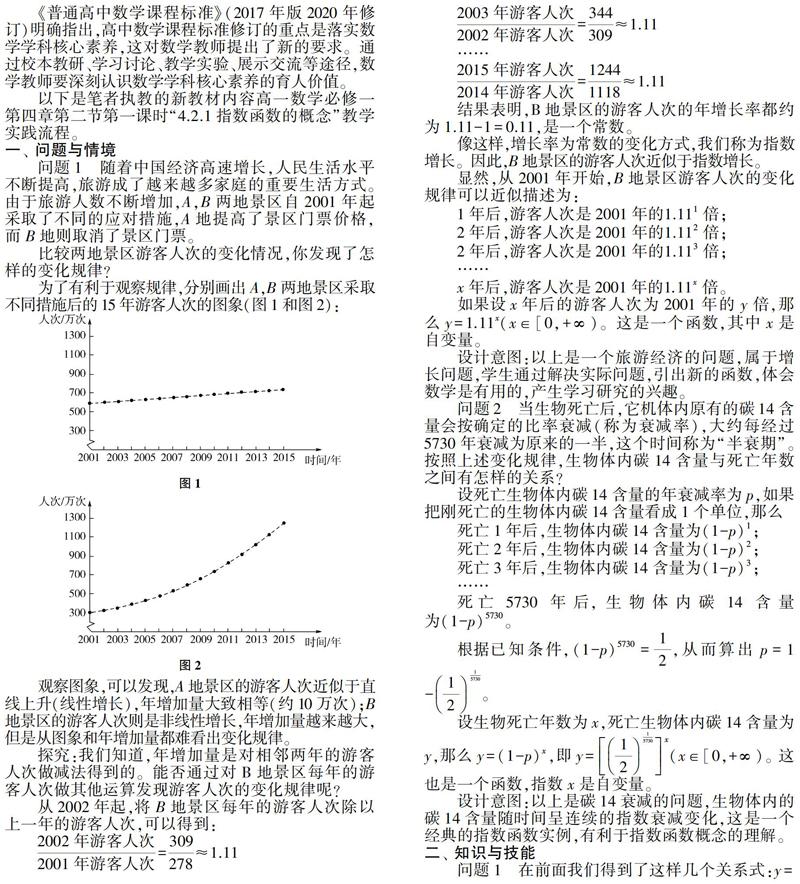
为了有利于观察规律，分别画出A，B两地景区采取不同措施后的15年游客人次的图象（图1和图2）：

观察图象，可以发现，A地景区的游客人次近似于直线上升（线性增长），年增加量大致相等（约10万次）;B地景区的游客人次则是非线性增长，年增加量越来越大，但是从图象和年增加量都难看出变化规律。

探究：我们知道，年增加量是对相邻两年的游客人次做减法得到的。能否通过对B地景区每年的游客人次做其他运算发现游客人次的变化规律呢？

从2002年起，将B地景区每年的游客人次除以上一年的游客人次，可以得到：

2002年游客人次2001年游客人次=309278≈1.11

2003年游客人次2002年游客人次=344309≈1.11

……

2015年游客人次2014年游客人次=12441118≈1.11

结果表明，B地景区的游客人次的年增长率都约为1.11-1=0.11，是一个常数。

像这样，增长率为常数的变化方式，我们称为指数增长。因此，B地景区的游客人次近似于指数增长。

显然，从2001年开始，B地景区游客人次的变化规律可以近似描述为：

1年后，游客人次是2001年的1.111倍;

2年后，游客人次是2001年的1.112倍;

2年后，游客人次是2001年的1.113倍;

……

x年后，游客人次是2001年的1.11x倍。

如果设x年后的游客人次为2001年的y倍，那么

y=1.11x（x∈[0，+∞）。这是一个函数，其中x是自变量。

设计意图：以上是一个旅游经济的问题，属于增长问题，学生通过解决实际问题，引出新的函数，体会数学是有用的，产生学习研究的兴趣。

问题2 当生物死亡后，它机体内原有的碳14含量会按确定的比率衰减（称为衰减率），大约每经过5730年衰减为原来的一半，这个时间称为“半衰期”。按照上述变化规律，生物体内碳14含量与死亡年数之间有怎样的关系？

设死亡生物体内碳14含量的年衰减率为p，如果把刚死亡的生物体内碳14含量看成1个单位，那么

根据已知条件，（1-p）5730=12，从而算出

设计意图：以上是碳14衰减的问题，生物体内的碳14含量随时间呈连续的指数衰减变化，这是一个经典的指数函数实例，有利于指数函数概念的理解。

二、 知识与技能

15730x，这几个关系式能否构成x和y之间的函数关系呢？

生答：可以，因为对每一个确定的x，都有唯一确定的y与之对应。

问题2 类似这样的函数，你能再举几个例子吗？这些函数有什么共同特征？能否用一般形式表示？

设计意图：启发和引导学生思考这类食物的本质属性是什么，让学生产生研究这一组新对象的兴趣，主动发现新问题。

共同特征：都是指数形式，自变量在指数位置，底数是常数。

问题3 形如y=ax（x∈R）的函数就是本节要学习的指数函数，自变量是x，底数a是常数。以上例子的不同之处，是底数不同。那么你觉得底数能取哪些值？底数的允许范围是什么？

设计意图：引导学生分析函数的定义域，进而讨论底数的允许值范围。

生答：底数不能取负数，如果底数取负数或0，x就不能取任意实数了。

师补充：为了研究的方便，我们要求底数a>0。另外，引导学生发现，当a=1时，函数就是常函数y=1，对于这个函数我们已经比较了解了，通常我们还规定a≠1。

通过讨论，得到体现自变量在指数位置这一本质特征的最基本、最简洁、最合理的形式：y=ax（a>0且a≠1），从而完成对指数函数概念的建构。

三、 新知运用

设计意图：不仅可以让学生熟悉指数函数的解析式和对应关系，还可以让学生学习利用函数解析式列方程求底数a的值。

例2 在问题1中，如果平均每位游客出游一次可以给当地带来1000元门票之外的收入，A地景区的门票价格为150元，比较这15年间A，B两地旅游收入变化情况。

这说明，在2001年，游客给A地带来的收入比B地多412000万元;随后10年，虽然f（x）>g（x），但g（x）的增长速度大于f（x）;根据上述数据并考虑实际情况，在2011年2月某个时刻就有f（x）=g（x），这时游客给A地带来的收入和B地差不多;此后，f（x）

设计意图：通过利用指数函数概念来解决问题，让学生进一步了解指数函数的实际意义，并理解指数函数的概念。同时引出形如y=kax（k≠0，a>0，且a≠1）的刻画指数增长或指数衰减变化规律的函数模型。

以上是基于新教材的“4.2.1指数函数的概念”教学课堂设计，与以往不同的是，指数函数的概念占据一个课时，而指数函数的图象和性质留做下一个课时的内容来进行探究，笔者认为新教材这样设计是合理且有必要的，有助于核心素养在课堂中的落实，以下对本节课内容进行分析：

1. 概念教学是培养数学抽象素养的落脚点

本节课从旅游人次的增长问题和碳14的衰减问题这两个实例引入指数函数的概念，让学生经历完整的数学抽象过程，从具体到抽象的深化，自然地提出问题，熟悉数学抽象的基本思路，顺利展开数学活动，在概念形成的学习中学会数学抽象。

2. 创设情境环节培养学生的数学建模素养

数学建模是对新鲜问题进行抽象，用数学语言表达问题，用数学知识与方法构建模型解决问题的过程。通过创设情境，有利于学生更好地感受指数函数模型，促进学生了解中国文化、关心社会。通过对问题情境的完美解决，有效提升了学生的数学应用意识，提高了学生的数学建模能力。

3. 思路探究环节发展学生的逻辑推理素养

数学是教思维的，数学是教推理的，数学是讲逻辑的。逻辑推理是指从一些事实和命题出发，依据逻辑规则推出一个新命题的思维过程。思路探究需要铺设合适的台阶，逻辑推理才能顺利进行。本节课的知识技能环节通过设计一系列的问题链，让学生不断地处于问题探究的过程之中，引发学生思维的碰撞。在探究过程中自然而然提升了逻辑推理能力。

4. 结论运用环节提升学生的数据分析素养

本节课的例题教学2与情景引入相呼应，对旅游人次的增长问题进行数据分析，从而比较A，B两地旅游收入变化情况。对数据进行整理和数据分析，是现代公民在信息化时代的基本能力和基本素养，数据分析是指针对研究对象获得相关数据，运用统计方法对数据中的有用信息進行分析和推断，形成知识的过程。通过例2的数据分析，学生不仅解决了实际问题，还能够从中体会指数函数模型的增长呈“爆炸”型增长。

数学核心素养是数学新课程对数学教学的新要求，也是课堂教学新的风向标。在新教材、新课标的大背景下，一线教师更应该注重在平常的教学活动设计中让学生主动建构知识，使得学生数学核心素养得以发展和提升。

参考文献：

[1]中华人民共和国教育部制定.普通高中数学课程标准（2017年版2020年修订）[M].北京：人民教育出版社，2017.

[3]水菊芳.基于数学核心素养的课堂数学意识的建构[J].数学通报，2016，55（11）：6-9.

[3]李昭平，方明洋.核心素养下概念教学的六个维度[J].数学通讯，2019（3）：8-11.

作者简介：朱晴晴，福建省厦门市，厦门双十中学漳州校区。