火灾中受伤人数多元线性回归模型建立与研究
王林

摘要:文章根据2009~2018年火灾受伤人数统计数据,运用多元线性回归方法,以电器火灾占比、生活用火不慎火灾占比、其他火灾占比为自变量,受伤人数为因变量建立多元线性回归模型,结果表明,生活用火不慎火灾占比、其他火灾占比对受伤人数产生显著性。
关键词:受伤人数;多元线性回归;回归模型;显著性
随着社会的快速发展,我国火灾频频出现,每年都有许多人在火灾中受伤。文章截取2009~2018年火灾受伤人数、电器火灾占比、生活用火不慎火灾占比、其他火灾占比统计数据建立多元线性回归模型,并对模型进行回归分析。
一、收集数据
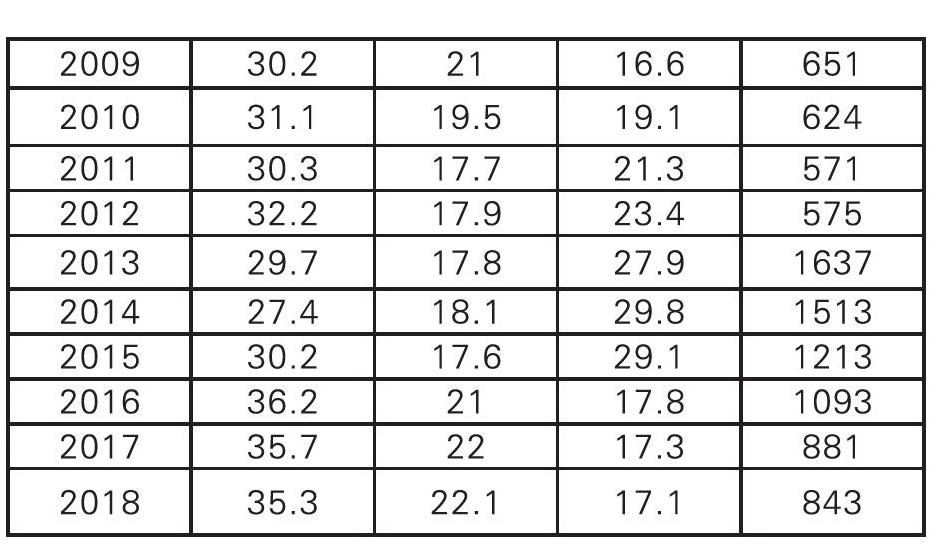
文章从中国消防救援年鉴中截取了2009~2018 年火灾中受伤人数、电器火灾占比、生活用火不慎火灾占比、其他火灾占比的相关数据收集如下表。
二、求解并建模
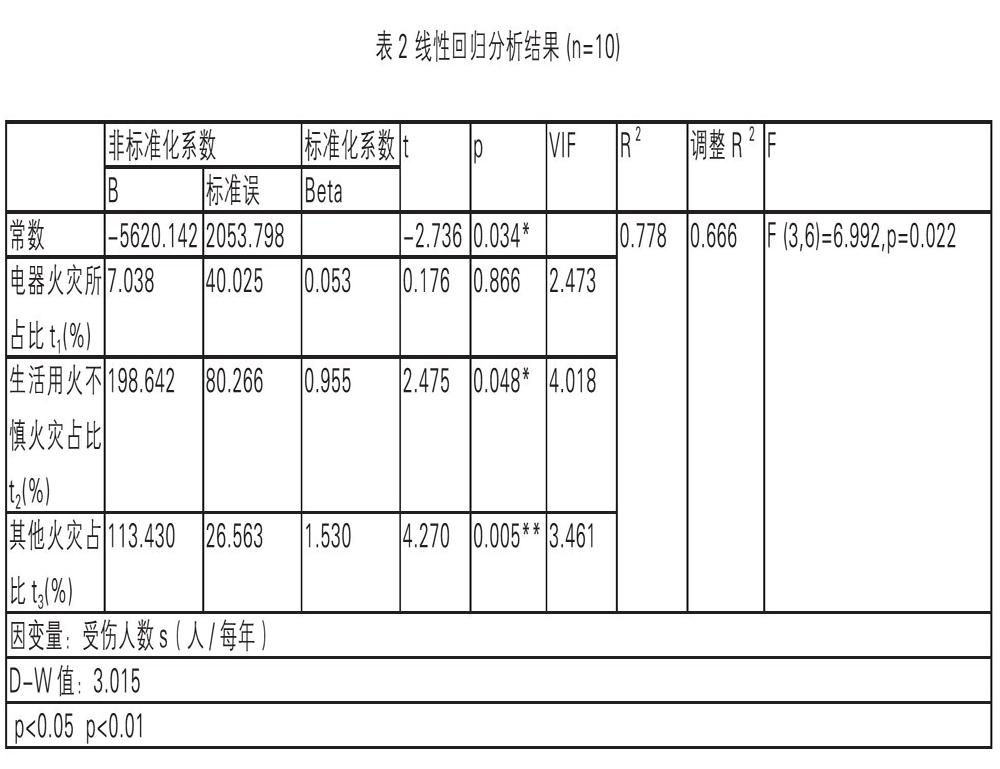
将表1中的数据上传到SPSS软件中,进入线性回归,点击开始分析可得线性回归分析结果。
按照电器火灾占比t1(%)、生活用火不慎火灾占比t2(%)、其他火灾占比t3(%)为自变量,受伤人数s(人/每年)为因变量,建立多元回归模型 。根据表2数据,可知多元线性回归模型表达式如下:
三、研究与分析
从上表2可以看出,模型R方值为0.778,它是反映电器火灾占比t1、生活用火不慎火灾占比t2、其他火灾占比t3对受伤人数s的联合影响程度。然后采用方差分析法(F檢验)对模型进行检验,其中F=6.992,p=0.022<0.05,也即说明三个自变量至少一项会对因变量产生影响关系。因为电器火灾所占比、生活用火不慎火灾占比、其他火灾占比的回归系数值分别为7.038(t=0.176,p=0.866>0.05)、198.642(t=2.475,p=0.048<0.05)、113.430(t=4.270,p=0.005<0.01),所以电器火灾所占比t1并不会对受伤人数s产生影响关系,生活用火不慎火灾占比t2、其他火灾占比t3会对受伤人数s产生显著的正向影响关系。
四、结语
文章通过建立模型,对回归系数进行显著性检验得出生活用火不慎火灾占比t2,其他火灾占比t3会对受伤人数s产生显著的正向影响关系。但是电器火灾所占比t1并不会对受伤人数s产生影响关系。
参考文献:
[1]杨雯婷.多元线性回归在广西粮食产量预测中的应用[J].科技展望,2015(30):149.
[2] 李智录,李抗彬. 雪冰融水型洪水预报模型建立与应用[J].西安理工大学学报,2006(03):253-256.
[3]范廷宾,王明.火烧云铅锌矿矿石小块体重多元线性回归模型建立及检验[J].地质学刊,2017(03):410-414.
[4]应急管理部消防救援局.2018中国消防年鉴[M].北京:应急管理部出版社,2018.
[5]徐志胜.安全系统工程[M].北京:机械工业出版社,2016:185-186.
[6]The SPSSAU project (2020). SPSSAU. (Version 20.0)[Online Application Software].Retrieved from https://www.spssau.com.
作者简介:
王林(1989—),男,汉族,硕士研究生,助理工程师,研究方向:灭火救援。

