融合自适应卡尔曼和小波的MEMS陀螺去噪方法

吴佳慧,冉昌艳,2

(1.三峡大学计算机与信息学院，湖北宜昌 443002；2.湖北省水电工程智能视觉监测重点实验室,湖北宜昌 443002)

0 引言

基于微机电系统(micro-electro-mechanical system,MEMS)惯性传感器的MEMS惯性导航技术是惯性导航技术的一个重要分支，因其系统具有成本低、体积小、功耗低以及抗冲击强等优点而被广泛应用于无人机导航系统中[1]。MEMS传感器是MEMS惯性导航系统的核心，其精度直接或间接影响了无人机导航的精度。然而，惯性MEMS传感器由于漂移会产生较大的噪声、偏置和尺度因子误差[2]，为提高无人机导航的鲁棒性，减少陀螺仪随机漂移误差，文献[3]和文献[4]都利用时间序列建模分析对陀螺仪进行卡尔曼滤波处理，验证了卡尔曼滤波在降低陀螺仪随机误差中的有效性。但忽略了MEMS陀螺仪信号中野值等干扰数据的影响。文献[5]采用小波去噪的算法对陀螺随机漂移有一定的抑制作用，但传统的小波分析都只是对信号的高频分量进行去噪处理，而忽略了低频分量的少许噪声。

针对以上问题，本文结合卡尔曼滤波和小波的优点，采用了将自适应抗野值卡尔曼滤波和改进的小波相结合的方法对陀螺仪的随机漂移误差进行处理。抑制了信号中野值对滤波发散的影响，提高了滤波精度。同时也更好地抑制了陀螺仪低频信号中的噪声，有效地提高了去噪效果。

1 MEMS陀螺随机漂移建模

时间序列分析作为一种数理统计分析方法，该方法根据平稳时间序列的变化规律建立差分方程，把一个高度相关的平稳时间序列表示成一个数字递推的形式。时间序列分析模型通常分为自回归滑动平均模型(ARMA)、滑动平均模型(MA)和自回归模型(AR)。统计特性表明，MEMS陀螺仪建模的阶数比较低，通常不超过3阶，且AR模型作为线性方程，在计算上比ARMA和MA模型更具优势[6-7],因此本文分别采用自回归模型AR(1)、AR(2)和AR(3)对MEMS陀螺仪随机漂移进行建模，采用最终预报误差FPE准则对模型参数进行估计[8]，估计结果如表1所示。

表1 AR模型参数估计结果

从表1可看出AR(3)的FPE最小，但是和AR(1)的FPE相差不大，在保证模型准确的情况下，为计算方便，本文选用AR(1)模型作为陀螺仪随机漂移模型：

mk+1=0.029 9mk+εk+1

(1)

式中：mk+1、mk分别为tk+1、tk时刻的陀螺仪误差；εk+1为均值为0、方差为σ的白噪声。

2 自适应抗野值卡尔曼滤波

陀螺仪输出信号中往往都含有野值，而这些野值通常会影响卡尔曼滤波效果，所以在文中采用一种自适应抗野值卡尔曼滤波,该滤波在卡尔曼的基础上根据信息对滤波增益和预测值进行了修正，更好地提高了滤波精度[9]。

假设系统的状态方程为

Xk+1=AXk+BWk

(2)

量测方程为

Zk+1=HXk+1+Vk

(3)

式中：Xk+1,Xk分别为tk+1，tk时刻的状态量；Zk+1为tk+1时刻的量测量；Vk为系统量测噪声，其值为AR(1)模型的估计误差，方差为R；Wk为系统过程噪声，其方差为Q,其值为AR(1)模型中白噪声εk+1的方差σ。

Wk和Vk的统计特性为

(4)

式中：∀k,s,δkk=1；δks=0。

卡尔曼滤波过程：

(5)

信息：

(6)

前k+1时刻信息序列ε(ε1,ε2,…,εk+1) 的方差:

(7)

以信息为中心，以信息序列的最大偏差为半径r1画圆，以β倍的信息序列的最大偏差为半径r2画圆，如图1所示。

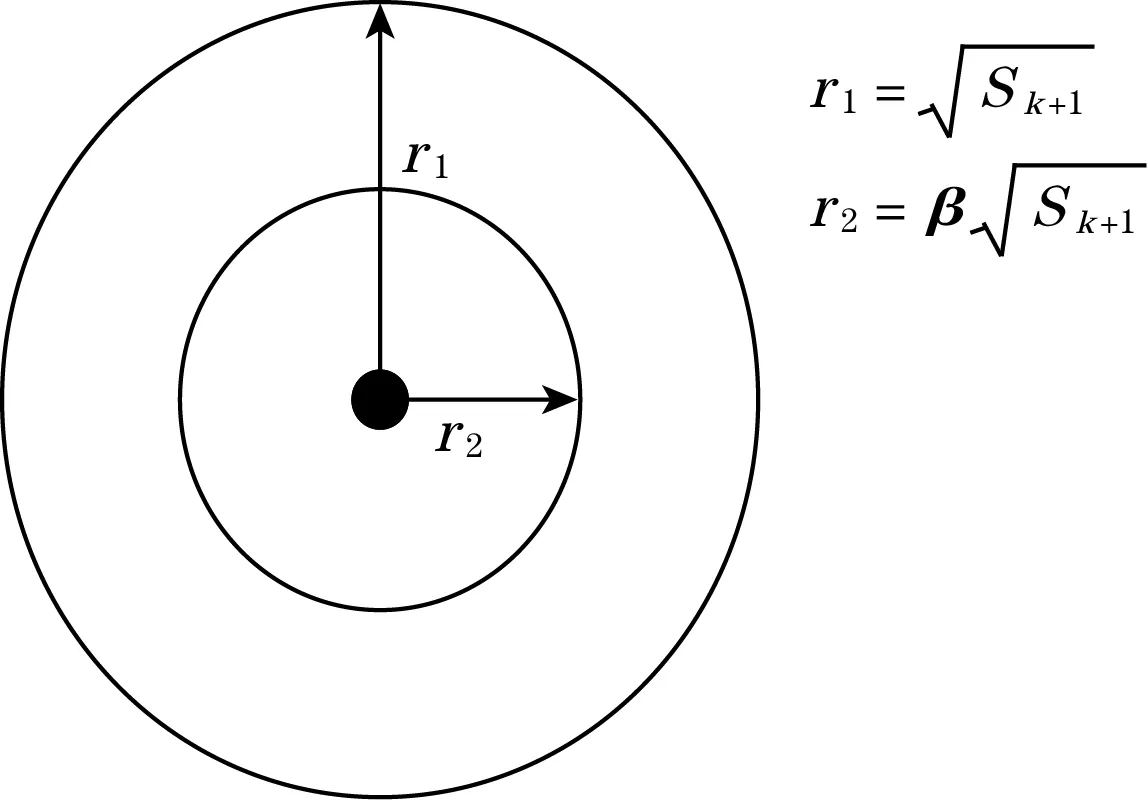
图1 抗野值滤波原理图

当‖εk+1|-|E(ε)‖>r1，则认为当前的观测数据是野值等于干扰数据，系统的主要偏差来源于观测值，则应降低当前时刻的滤波增益，减少观测值对系统的状态估计占有的权重，重新计算k+1时刻的卡尔曼滤波增益,修正公式为

Kk+1=αKk+1，α∈(0,1)

(8)

(9)

当‖εk+1|-|E(ε)‖≤r2，则认为观测和预测数据都正常，不做任何修正。自适应抗野值卡尔曼流程图如图2所示。

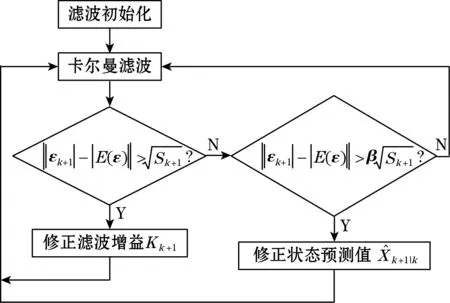
图2 自适应抗野值卡尔曼流程图

3 改进的小波去噪

传统的小波去噪就是把含噪信号进行小波变换，根据小波系数之间的关系或者相应的准则设定一个阈值，进而对变换后的小波系数的高频分量进行处理，保持低频分量不变，得到新的小波系数，最后对其小波逆变换，得到去噪信号。

在典型的MEMS陀螺系统中，采用Allan方差对MEMS陀螺仪进行噪声分析和性能评估，能够准确地测出MEMS陀螺仪常见的噪声系数：量化噪声、角度随机游走和零偏不稳定性等[10-11]。量化噪声是陀螺仪输出端的高频分量，而角度随机游走和零偏不稳定性都是长期的低频现象[12]。因此，本文中采用了一种先选择分解水平，并对该层的低频分量和每一层的高频分量同时进行阈值处理的方法，对MEMS陀螺仪信号进行了去噪处理。

小波分析中，信号的能量通常集中体现在小部分幅度比较大的小波系数上，而噪声的频率和能量谱相对分散，因此噪声的小波系数绝对值比较小，且能量分散在大部分的小波系数上[13]，随着分解层数的增加，噪声信息在高频分量中所占比例逐渐减少，有用信号所占比例逐渐增加，当噪声含量非常小而无法区分时，此时对该层的低频分量也进行阈值去噪可以更好地抑制陀螺仪的低频噪声。

(1)对带噪信号进行小波分解，确定分解级别；为了得到噪声阈值化的分解水平，首先需要计算每层高频分量的PSR，即

(10)

式中：max|Wn|为位于第n层的高频分量的绝对值的最大值；|Wn,i|为位于第n层第i个高频分量的绝对值；Nn为第n层高频分量的个数；Sn可以识别高频分量中的噪声，当Sn≤ρ，Sn+1>ρ,ρ∈(0,1)时，其中ρ为区分某层高频分量是否含有噪声的一个阈值，高频分量只包含信号系数。那么分解层数k=n[14]。

(2)对每层的高频分量阈值化处理，并对选定分解级别的低频分量也阈值化处理；

(3)对处理后的高频分量和低频分量进行小波重构，得到去噪信号。

4 实验仿真

将MEMS陀螺仪静置于实验转台进行实测，静置时间为1 h，采样频率为200 Hz。对实测数据进行融合卡尔曼和小波的去噪方法进行实验，融合卡尔曼和小波去噪流程图如图3所示，并利用Allan方差对陀螺仪噪声系数进行评估，陀螺仪x、y、z轴的去噪效果对比图如图4、图5、图6所示，陀螺仪x、y、z轴的噪声系数对比分别如表2、表3、表4所示。

图3 融合卡尔曼和小波去噪流程图

图4 MEMS陀螺仪x轴去噪效果分析

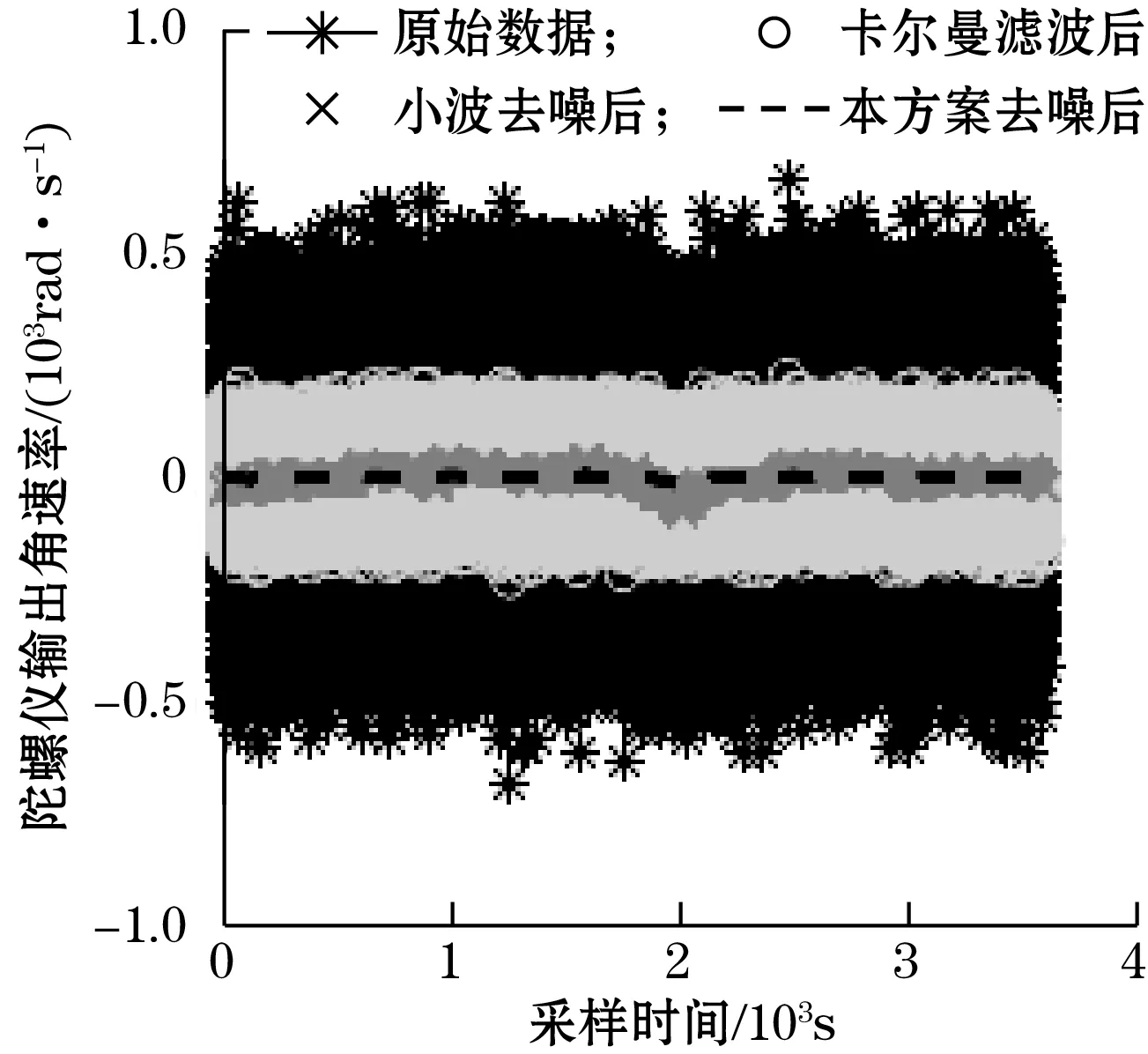
图5 MEMS陀螺仪y轴去噪效果分析

图6 MEMS陀螺仪z轴去噪效果分析

表2 陀螺仪x轴噪声系数对比分析表

从表2、表3、表4可以看出，本方案去噪后所估计的量化噪声系数、角度随机游走和零偏不稳定性均小于卡尔曼滤波和Visushrink小波去噪。

表3 陀螺仪y轴噪声系数对比分析表

表4 陀螺仪z轴噪声系数对比分析表

陀螺仪x、y、z轴去噪后方差对比如表5所示。从表5可以看出，本方案去噪后方差均小于卡尔曼滤波和Visushrink小波去噪。

表5 陀螺仪x、y、z轴方差对比分析表 (°)2/s2

5 结论

针对MEMS陀螺输出信号噪声大、有野值等问题，本文采用一种融合卡尔曼和小波的自适应抗野值去噪方法对MEMS陀螺仪进行了降噪处理，通过Allan方差分析估计陀螺仪噪声系数，并与卡尔曼滤波方法和Visushrink小波去噪方法进行对比分析，结果表明本文方法的量化噪声系数、角度随机游走和零偏不稳定性均小于卡尔曼滤波和Visushrink小波去噪，尤其陀螺仪x、y、z轴零偏不稳定性在本方案下比卡尔曼滤波分别提高了31.0%、29.3%、30.5%，比Visushrink小波去噪分别提高了2.4%、12.1%、12.4%。