试题呈现有新意 试题解决要创新
——2020年北京市高考适应性测试数学第10题解析
王芝平 肖志军
(1.北京宏志中学 100013;2.北京工业大学附属中学 100022)
试题再现学业水平测试成绩按照考生原始成绩从高到低分为 A,B,C,D,E五个等级,某班共有36名学生且全部选考物理、化学两科,这两科的学业水平测试成绩如图所示. 该班学生中,这两科等级均为A的学生有5人,这两科中仅有一科等级为A的学生,其另外一科等级为B. 则该班( )

等级科目 ABCDE物理1016910化学819720
A.物理化学等级都是B的学生至多有12人
B.物理化学等级都是B的学生至少有5人
C.这两科只有一科等级为B且最高等级为B的学生至多有18人
D.这两科只有一科等级为B且最高等级为B的学生至少有1人
试题解析题目以表格的方式呈现了物理、化学两科学业成绩各等级的人数,而选项要求我们判断获得某种成绩的人数情况,如前两项是判断物理、化学等级都是B的学生人数范围,后两项是判断物理、化学两科成绩中只有一科等级为B且最高等级也是B的学生人数范围.
所以我们应想一想,在这次测试中,所有可能的成绩有多少种?每一种成绩对应多少学生?
在计数原理、古典概型的学习中,我们研究过一些计数问题,其中一些问题可以用表格帮助我们思考.如,我们曾经研究过投掷两枚骰子的问题,即:
例同时掷两个骰子,计算向上的点数之和是5的概率是多少?(人教社高中数学A版必修3)
这个问题的一种解决方法(未必是简单方法,成绩好的同学可以不用列表)是列表如下:

1234561(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)2(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)3(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)4(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)5(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)6(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)
两个骰子分别记作第Ⅰ枚骰子与第Ⅱ枚骰子.以行表示第Ⅰ枚骰子向上的点数,以列表示第Ⅱ枚骰子向上的点数.
通过观察这个表格,很容易发现两个骰子向上的点数的结果共有36种,其中向上的点数之和是5的结果共有4种,这种方法能有效避免错误.

物理化学 ABCDE合计A530008B5a11a12a13019C0a21a22a2307D0a31a32a3302E000000合计101691036
类比上述过程,我们可以自己设计一个表格,行与列分别表示化学与物理的成绩等级,如图1所示.即“A行”表示化学成绩等级为A时,物理成绩各等级对应的人数;“B列”表示物理成绩等级为B时,化学成绩各等级对应的人数.所有可能的成绩共有25种.
把已知的数据填入这个表格,该班学生中,这两科等级均为A的学生有5人,则A行A列填5;又“这两科中仅有一科等级为A的学生,其另外一科等级为B”,所以,B行A列填5;A行B列填3;从题设表格知,E行与E列填0.
而前两个选项显然是想让我们判断出物理、化学两科等级都是B的学生人数范围,即B行B列位置上的数字(a11)范围;
后两个选项是判断两科成绩只有一科等级为B且最高等级为B的学生的人数范围,即表中a12、a13、a21、a31四个数字之和的取值范围.
那么,我们从哪个选项入手呢?当然是从容易判断正确或错误的选项入手,正确得到的话,答案就出来了,否则就排除这一选项.
前三个选项一时不易判断,第四个选项数字最小,且“至少”的反面比较简单——若该选项不成立,则这两科只有一科等级为B且最高等级为B的学生有0人,这样很快得到一些确定的信息:a12=a13=a21=a31=0.
从B列上看,a11+3=16,即a11=13;从B行上看,a11+5=19,即a11=14.
得出矛盾的两个结论,这说明假设是错误的!所以D必正确. 选D.
反思与启迪本题以学生熟悉的学业成绩为素材,巧妙设计趣味推理型试题,不仅情景真实、贴近学生生活,还有效地避开学生已有的解题套路与现成的公式,体现了数学的人文价值,深入考查了逻辑推理能力和创新应用能力.
数学中的表格既能直观呈现题目的已知信息,又可以把题目的隐含信息表现出来.所以数学学习要善于读图、读表和用图与表格表达信息.
面对呈现方式和设问方式的创新设计,要善于从题设中提取信息、从设问中确定所需要的信息,学生在理解问题本质的基础上,根据自己数学思维活动经验(记忆系统中储存的数学信息)选取有关的信息,寻找解题的依据,设计解题策略,寻求合适的解题工具、探索解决问题方法,梳理解题程序,最后用数学语言严谨、有序地进行论证、求解.
人类之所以超脱了动物而成为地球的圣灵,原因之一就是发明了自己的语言和文字.数学符号是语言文字范畴中最原始、最精华的部分,数学符号的灵活运用则构成了人类思维与创造的美妙图案.
我们从简单选项入手,通过否定该选项推出矛盾而确认该选项的正确性,最终做出正确选择.如果我们不满足于答案的获得,那么应该追问自己,前三个选项为什么是错误的呢?能构造出说明它们是错误的具体例子吗?思维的深刻性是重要的思维品质.

物理化学 ABCDE合计A530008B51301019C007007D002002E000000合计1016910
要想说明第一个选项“A.物理化学等级都是B的学生至多有12人”是错误的,就要构造物理与化学等级都是B的学生至少有13人的具体例子,为此我们假设物理与化学等级都是B的学生有13人(从B列上看,B行B列处的数最大是13),即a11=13,则a21=a31=0且a12+a13=1.
若a12=0,a13=1,如图2所示,若a12=1,a13=0,如图3,图4所示,

物理化学 ABCDE合计A530008B51311019C007007D001102E000000合计1016910
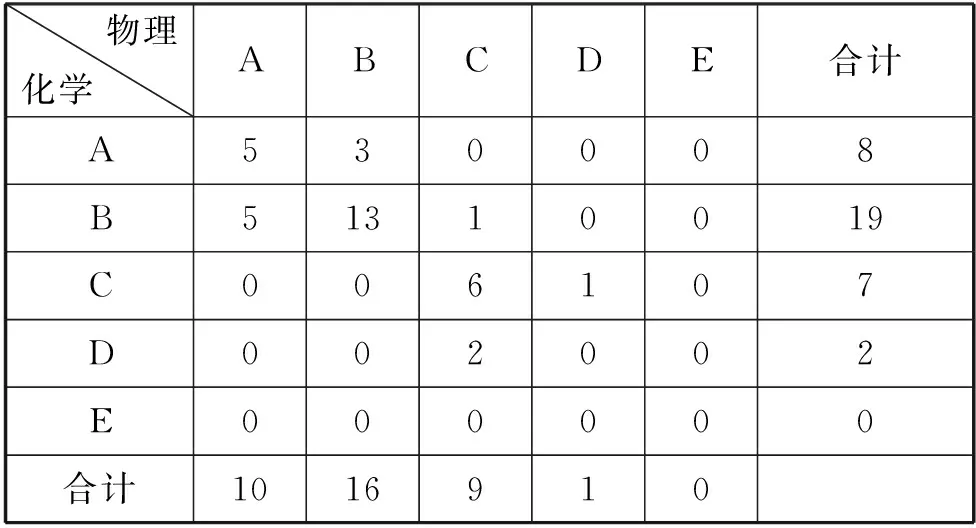
物理化学 ABCDE合计A530008B51310019C006107D002002E000000合计1016910
以上三个例子都说明选项A是错误的.
为了说明第二个选项“B.物理化学等级都是B的学生至少有5人”是错误的,则应假设物理与化学等级都是B的学生有4人,则a12+a13=10,又a12≤9,a13≤1,
所以a12=9,a13=1.所以a22=a23=a32=a33= 0,故a21=7,a31=2. 如图5所示.

物理化学 ABCDE合计A530008B5491019C070007D020002E000000合计1016910
这就说明选项B,C都是错误的.
构造正例与反例是数学学习中的一项基本思维活动.

