箱式无蜗壳风机箱体的优化设计

侯佳鑫 赵 琛 谢军龙 吴 鑫

（华中科技大学能源与动力工程学院）

0 引言

箱式无蜗壳风机是一种新型离心风机，也是新风机组的重要组件，主要用于空调设备和建筑通风等领域[1]。与有蜗壳风机相比，箱式无蜗壳风机具有结构简单、静压效率高、噪声低、体积小、出风方向任意等优点，且符合风机设备向低能耗、低噪声、小体积的变化趋势[2]，具有广阔的应用前景。但箱式无蜗壳风机能效差，相对于传统离心风机，箱式无蜗壳风机出口静压低，总效率最高为58%～63%，无法达到传统离心风机的水平[3]。

为提高箱式无蜗壳风机性能，研究人员对风机的优化设计方法进行了大量的研究。马寅辉等[4]对无蜗壳风机进行分析后，认为风机内的能量损失在低流量工况下主要由叶片吸力面分离涡导致，在高流量工况下主要由二次流等因素导致。刘怀耀等[5]将同一叶轮放入不同尺寸的箱体内进行模拟，发现箱体尺寸大小对无蜗壳风机全压效率有影响，并认为箱体越接近蜗线效率越高。吴飞等[6]采用响应面法对风机箱体进行综合优化，优化后模型静压和效率有显著提升。

但目前国内外针对箱体内气流流动情况及结构参数设计优化方法的研究较少，且缺乏定量的数据进行详细说明。本文采用计算流体动力学方法进行模拟仿真计算，分析箱体内部产生流动损失的主要原因，并以叶轮外径作为参照基准，研究箱体结构参数对风机性能的影响规律，确定最佳箱体结构参数，为后续设计高效节能的箱式无蜗壳风机提供参考依据。

1 数值模拟

1.1 模型简化

箱式无蜗壳风机整机模拟仿真时其三维模型主要由风管、集流器、叶轮、电机、箱体五个部分组成。在三维建模阶段，对模型进行简化，仅保留叶轮部分的厚度，忽略部分工艺与零件，简化后箱式无蜗壳风机三维模型如图1 所示。风机结构参数如表1 所示，箱体参数示意图如图2 所示。风机在额定工况下的转速为2 330r/min，风量为500m3/h。

表1 原型机结构参数Tab.1 Prototype structure parameters

图2 箱式无蜗壳风机结构参数示意图Fig.2 Parameter diagram of plenum fan

为增加研究成果的实用性，同时为后续研究提供理论依据，本文在描述箱体尺寸时以叶轮外径D作为基准。

1.2 网格划分及无关性验证

根据风机的几何结构，使用专业网格划分工具对各个流体域进行非结构网格划分。叶轮域流动剧烈，流动情况复杂，为保证计算准确性，对叶轮域的网格进行加密处理。风机子午面网格如图3所示。

图3 风机子午面网格Fig.3 Fan meridional grid

为保证计算结果的可靠性和准确性，对箱式无蜗壳风机的网格数量与额定工况下的数值模拟结果进行网格无关性验证。由表2可知，当网格数量由187万增加至499万，风机静压趋于稳定。综合考虑计算精度和计算效率，箱式无蜗壳风机数值模拟网格数量确定为187万。

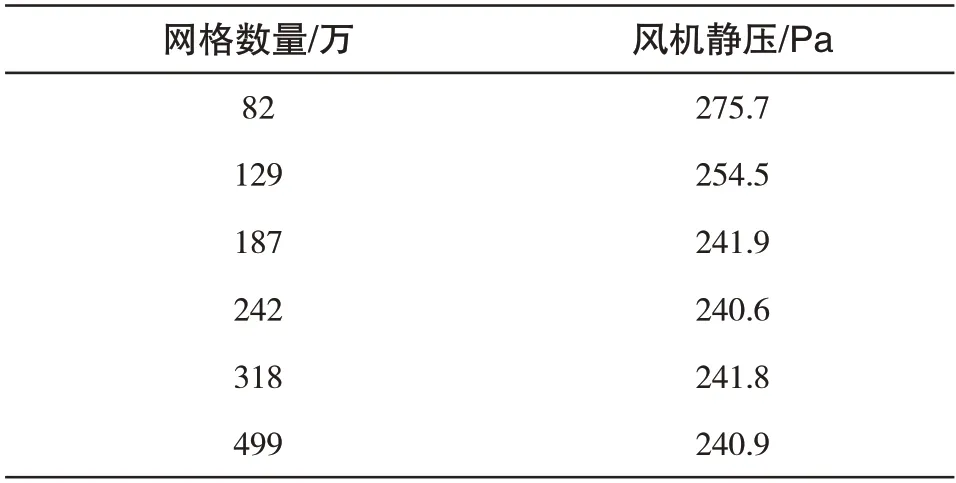
表2 不同网格数量下的风机静压Tab.2 Static pressure of fans with different grid numbers

1.3 边界条件

对箱式无蜗壳风机进行定常模拟，叶轮流体域采用旋转坐标系，风管进口设置为速度进口边界，箱体出口设置为压力出口边界，表压值为0Pa。

风机内部流动受限，导致雷诺数较大，故用湍流模型进行计算，选用标准k-ε 模型[7-8]，速度场和压力场的耦合计算采用SIMPLE方法[9]，当收敛精度小于10-3且进出口压力稳定，即认为达到收敛标准。采用上述计算方法对箱式无蜗壳风机进行数值模拟计算。

1.4 模型验证

为检验原型机数值模拟结果的准确性，将其与某厂提供的试验结果进行比较。

图4 为数值模拟与实验结果对比，由图可知，数值模拟与试验获得的性能曲线趋势相似，吻合较好，最大偏差仅为0.5%。表明本文采用的物理模型和计算方法准确可信，可用于指导下一步的研究工作。

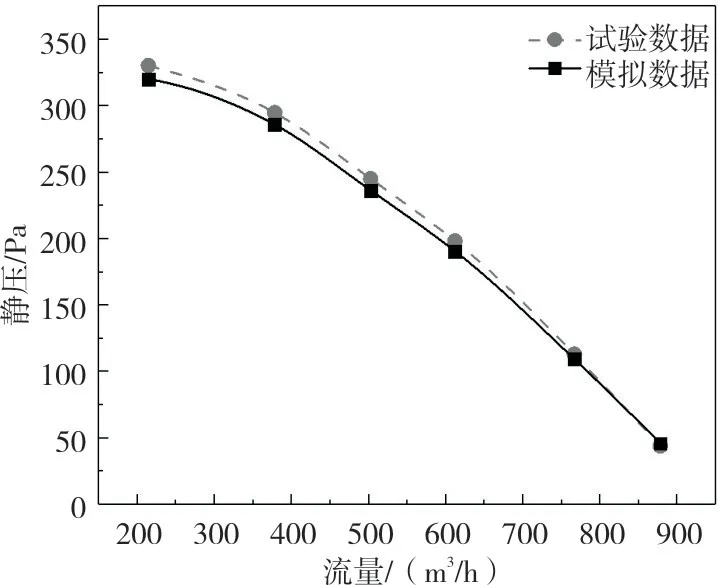
图4 数值模拟与试验结果对比Fig.4 Comparison of experiment and simulation

2 箱体流场分析

模拟风机在额定工况下的运行状态，获取箱体内静压分布云图，速度分布云图与气流运动轨迹，并分析能量损失的主要原因。

图5 和图6 分别为风机多截面速度分布云图和子午面流线图，中间空白区域为电机。由图5 可知，气体由集流器进入，在通过叶轮时气流速度逐渐增加，在叶轮出口处气流速度达到最大值。气流在箱体中流动时，近壁面的气流流速大于箱体中间区域的流速。由图6可知，叶轮甩出的气体呈弧状冲击箱体壁面后沿壁面流动，直至离开箱体。风机流道中存在定向高速强气流和无序低速弱气流，流道中的强气流无法带动弱气流定向流动，这一现象在箱体中心区域表现最为明显。叶轮甩出的气体撞击箱体壁面后分别流向出口侧与进口侧。箱体内部出现多处旋涡，一部分是箱式无蜗壳风机轴向送风时，气流沿箱体壁面流动时产生流动分离，在箱体内部形成旋涡,如A区所示；另一部分是叶轮甩出的气流撞击壁面后流向进口侧，形成旋涡，如B区所示。旋涡占据流道中心部分较大区域，主流被迫在箱壁四周发展，流通面积受限，导致流动损失加大。

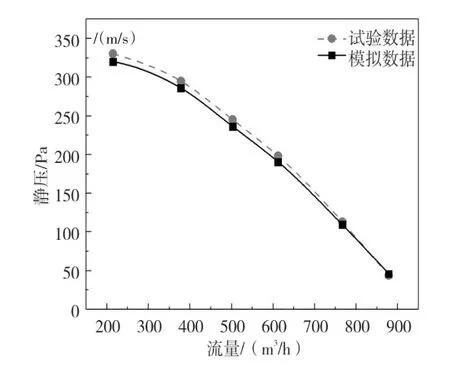
图5 风机多截面速度分布云图Fig.5 Fan multi-section velocity distribution

图6 子午面流线图Fig.6 Meridional streamline diagram

图7为箱体内部三维流线图，红色箭头标注出气流流动方向。由图可知，高速气流冲击箱体壁面后继续沿壁面流动，但气流速度降低且流动方向出现偏移，从风机进口侧观察，箱体内气流呈现顺时针运动和水平轴向运动叠加出的螺旋状运动。图8 为风机多截面静压分布云图，由图可知，箱体近壁面区域静压高，中心静压低，气体冲击箱体壁面时静压达到最大值。对于轴向送风的箱式无蜗壳风机，气流撞击箱体壁面的情况不可避免，易造成较大的冲击损失。

图7 箱体内部三维流线图Fig.7 Three dimensional streamline diagram inside the box

图8 风机多截面静压分布云图Fig.8 Fan multi-section static pressure distribution

综上所述，轴向送风的箱式无蜗壳风机内存在两处主要的能量损失：一处是旋涡占据较大流通空间，主流流通面积受限引起的流动损失；另一处是高速气流撞击箱体壁面造成的冲击损失。

3 箱体结构参数研究

箱体是箱式无蜗壳风机的重要组成部分，箱体尺寸过小会增加风机内部流动损失，箱体尺寸过大会增加制造成本，箱体结构参数进行优化可以提高风机的实用性和经济性。

3.1 箱体宽度对风机性能的影响

在原型机基础上，利用数值模拟方法，获取箱体宽度为1.4D、1.6D、1.8D、2.0D 时的风机性能曲线，如图9所示。由图可知，在额定工况下，随箱体宽度增大，风机静压呈现先增大后减小的趋势，当箱体宽度为1.8D时，风机静压达到最大值。且在小流量范围内，箱体宽度对风机静压影响较小，随着流量增大，叶轮出口速度提高，使冲击箱体壁面造成的能量损失越来越大，箱体宽度对风机静压的影响也越来越显著。冲击壁面造成的能量损失是箱式无蜗壳风机的主要能量损失之一。

图9 不同箱体宽度风机性能曲线Fig.9 Performance curve of fans with different box width

由于流量为800m3/h 时，不同箱体宽度下的静压压差较大，且箱体宽度为2.0D 时的静压比1.8D 时的静压不升反降的趋势明显，故对此工况下的箱式无蜗壳风机不同箱体宽度下的流线图进行分析。

图10为800m3/h不同箱体宽度流线图。如图所示，在四种不同的箱体宽度下，受二次流影响，叶轮出口处均存在出口流速不均匀现象，叶轮甩出的气体撞击壁面后分两个方向沿壁面流动，流向进口侧的气流形成旋涡。箱体宽度为1.4D时，箱体空间较小，从叶轮流出的气体冲击壁面时气流速度最高，撞击壁面造成的能量损失最大，导致箱体宽度为1.4D 时风机静压最低。当箱体宽度为2D 时，叶轮流出的气体进入一个较大的箱体空间，静压升高，速度降低，气流撞击箱体壁面时速度过小，出口流向偏移，导致叶轮出口处流向进口侧的气流增多，箱体内部流动损失增加。

综上所述，箱体宽度为1.8D 时风机静压最高。箱体宽度过小，叶轮甩出的气流高速冲击壁面造成的能量损失较多；箱体宽度过大，叶轮出口空间过大导致气流减速增压，叶道内形成显著的二次流，产生额外的能量损失。

图10 800m3/h不同箱体宽度流线图Fig.10 800m3/h Streamline diagram of different box width

3.2 箱体出口面积对风机性能的影响

在最佳箱体宽度N=1.8D的基础上进行箱体出口面积（M×M）的研究。分别选取出口面边长M 为0.7N、0.8N、0.9N、1.0N 来探究出口面积对风机性能的影响规律。图11为不同出口面边长风机性能曲线，由图可知，在小流量范围内风机静压随着出口面积的增大而增大；当流量进一步增大，出口边长为0.8N、0.9N、1.0N 的风机性能曲线重合度高，出口边长为0.7N 的风机静压明显偏小，表明当流量较大时，适当减小出口面积对风机性能影响较小。

图12为额定工况下箱体出口面边长分别为0.7N和1.0N 时的箱体流线图，由图可知，由于出口面积变小，气流冲击箱体壁面后速度降低，呈现出集中收缩的状态，如图12 中A 区所示。强气流被迫带动弱气流进行定向流动，并与箱体中部回流气体混合，加剧了流动的不稳定性，导致箱体内部旋涡数量增加，旋涡内气流流速增高，流动过程中的能量损失加剧。

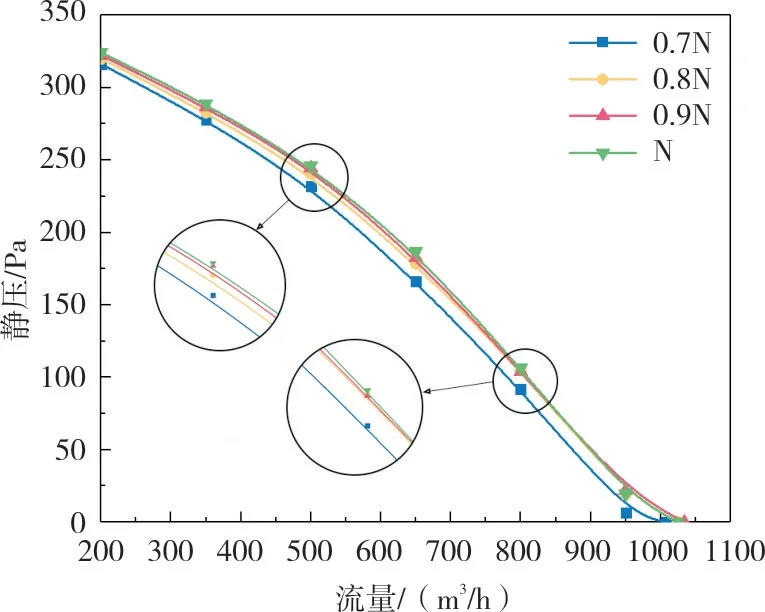
图11 不同出口面边长风机性能曲线Fig.11 Performance curve of fans with different outlet side lengths

图12 不同出口面边长流线图Fig.12 Streamline diagram of different exit width

当箱体出口宽度M 小于等于0.7 倍箱体宽度N 时，应在叶轮出口处与箱体出口处设置导流板，以改善箱体内部流动情况，提升风机性能。

3.3 箱体轴向长度对出口面流动均匀性的影响

在前两节的基础上，采用箱体宽度N=1.8D，箱体出口面边长M=N的箱体，定义箱体轴向长度L=B+L1，L1为叶轮后盘距箱体出口的轴向距离。分别取L1为0.1D、0.3D、0.5D、1.0D、1.5D、2.0D、3.0D、4.0D展开研究。

箱体轴向长度增加，有利于气体在箱体内部充分混合，增加出口面流动均匀性。分析轴向长度对风机出口面流动均匀性的影响，图13 为额定工况下不同轴向长度风机出口速度分布云图。由图可知，沿箱体壁面气流速度最高，从四周向中心气流速度呈梯度变化。当轴向长度L1＜0.5D 时，回流空间较大，箱体中间区域气流流速较低；当轴向长度0.5D ≤L1≤3.0D 时，受出口回流影响，出口面中心区域速度高于周边速度。当轴向长度L1=4.0D时，出口中心由回流导致的速度较高的区域消失，且箱体壁面处气流流速变化均匀。随着箱体轴向长度增加，出口面流速均匀性提高，中心区域低速区范围减小，表明气流逐渐流向中心区域，箱体内强气流与弱气流在箱体内部混合，使出口流速趋向均匀，但气流混合程度有限，出口面仍存在严重的流动不均匀现象。

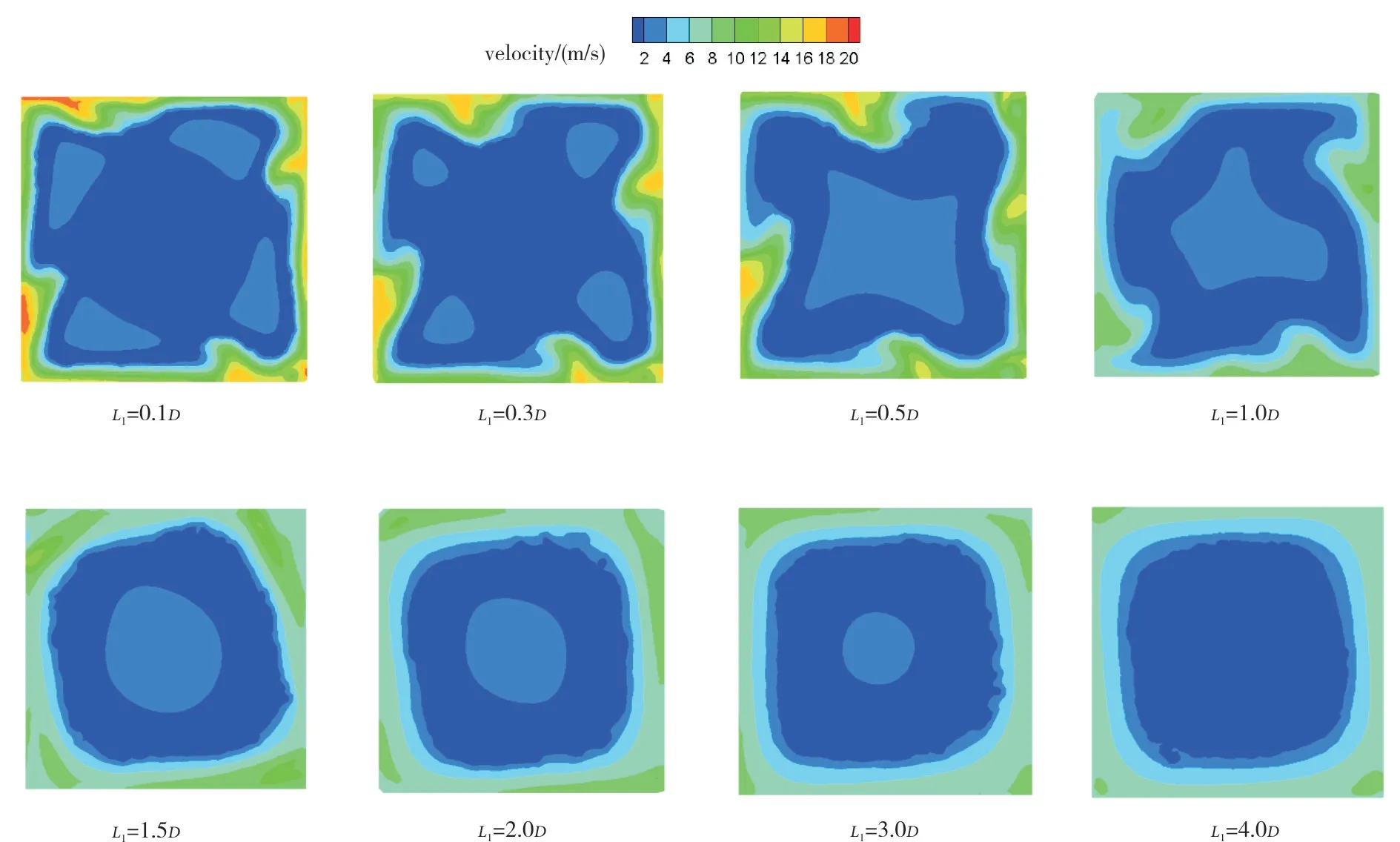
图13 不同轴向长度风机出口速度分布云图Fig.13 Outlet velocity distribution of fans with different axial lengths

进一步延伸箱体轴向距离L1=20D探究出口面产生回流的原因。图14 为轴向长度L1=20D 风机子午面流线图，图中仅展示箱体前半部分流线，箱体后部流动保持稳定，数据标签标注出所在点的气流流动速度。由图可知，叶轮甩出的气体沿壁面流动形成贴壁射流，伴随出现射流卷吸现象，射流对周围静止流体的夹带作用使箱体中心区域形成低压区，周围流体向低压区流动形成旋涡。当箱体轴向长度较短时，就表现为出口处的回流现象。

随贴壁射流的发展，射流断面不断扩大且流速逐渐降低，气流逐渐向箱体中间区域倾斜，开始混合。射流的卷吸作用是导致射流偏转的内在原因，射流使箱体内部产生压力差，在此压差的作用下，射流发生偏转。

定义叶轮后盘径向位置近壁面处的速度为射流初始速度，如图14中A点所示。额定工况下，旋涡贴近叶轮出口，受出口气流影响，旋涡中心处流速较高，对风机出口处气流流通区域产生较大的挤压作用，使有效流通面积减小，导致射流初始速度升高。

在大流量下，出口气流偏移，直接流向风机出口侧的气流减少。旋涡中心远离叶轮出口，中心处流速较低，旋涡区范围较小，对气流的挤压作用较小，气流有效流通截面相对较大。流量小与流通截面大导致大流量下射流初始速度较低。同时，大流量工况下同一截面速度差较小，如M截面所示，此时箱体内部流动稳定性相对较高。因此，大流量工况下射流卷吸能力下降，卷吸量减小，箱体内部气流混合提前。

叶轮甩出的气体沿壁面流动，表现为贴壁射流，射流卷吸现象使箱体内部产生旋涡，同时在有限长度内出口面出现回流现象。箱体轴向长度增加至4D 时，出口面回流基本消失，但仍存在较为严重的出口面流动不均匀性现象。

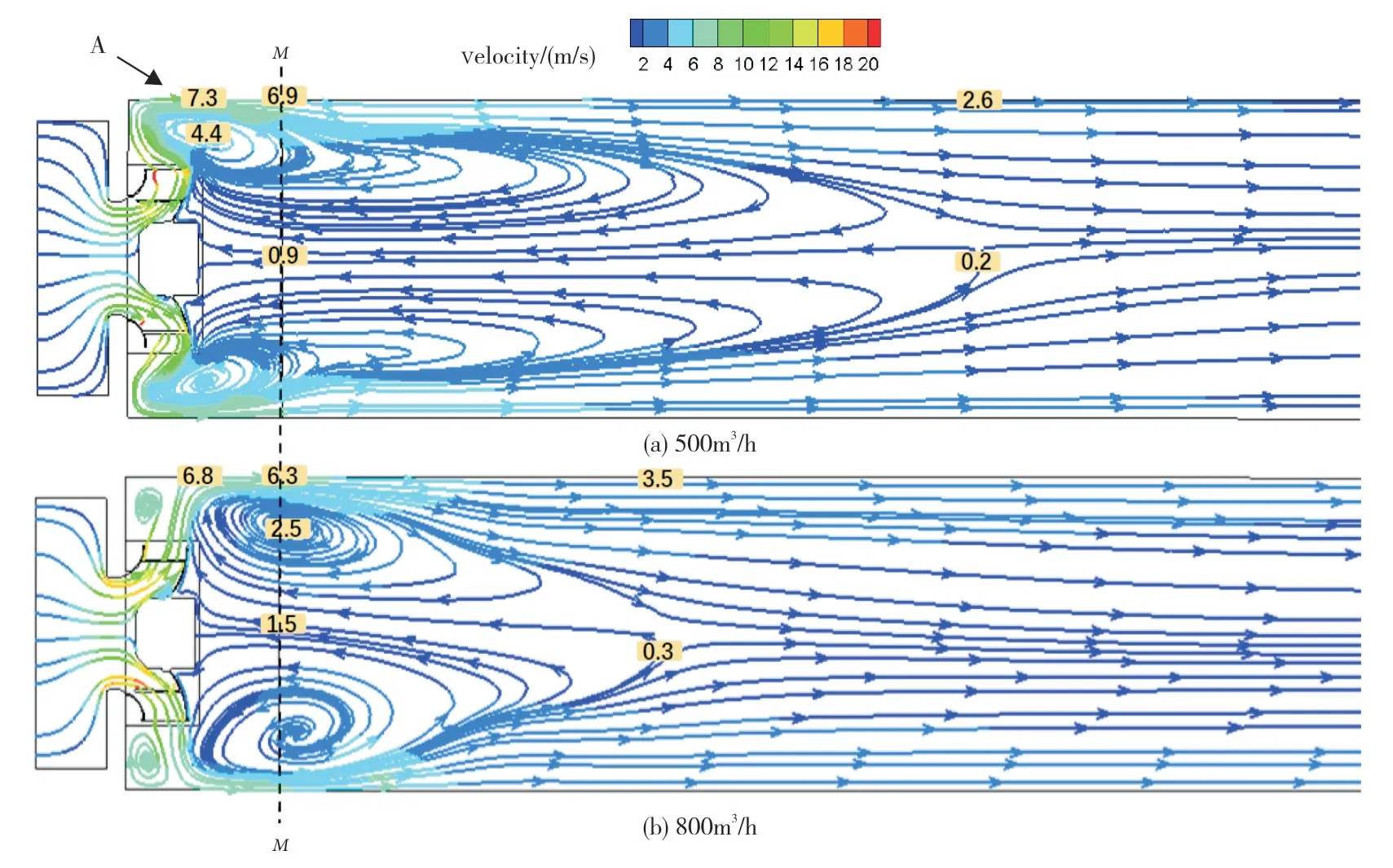
图14 轴向距离L1=20D风机子午面流线图Fig.14 Axial length L1=20D meridional plane flow diagram of the fan

4 结论

本文利用计算流体动力学方法研究箱式无蜗壳风机箱体内部产生流动损失的主要原因，并分析箱体结构参数对风机性能的影响规律，结论如下:

1）主流流通面积受限造成的流动损失和高速气流撞击箱体壁面造成的冲击损失是轴向送风的箱式无蜗壳风机产生能量损失的主要原因。

2）箱式无蜗壳风机最佳箱体宽度为1.8D；箱体出口宽度小于等于0.7倍箱体宽度时，应在叶轮出口处与箱体出口处设置导流板，以改善箱体内部流动情况。

3）叶轮甩出的气体沿壁面流动形成贴壁射流，出现射流卷吸现象，导致有限长度内的箱体出口面产生回流。