离心泵振动传递路径重合的解耦方法*
彭德锋 代月帮 李宏坤
(大连理工大学机械工程学院)
0 引言
传递路径分析(Transfer Path Analysis)[1]是一个非常有价值的工程工具,能够有效地分析振动噪声的来源与传递方式。传递路径分析的目的是降低噪声与振动,提高产品的舒适度或隐秘性。该方法除了应用于汽车的发展,还可以在船舶、航空航天、核电工程等领域应用。TPA涉及到主动部件(如发动机、转子系统)与被动结构(与主动部件相连接的结构件),当系统的主动部件的振动机制特别复杂致使无法建模或者无法被测量时,我们可以用被动面上的力或者振动来替代振动源[2]。
随着技术需求的不断变化,由经典TPA[3]技术衍生出多种TPA技术,例如:工况传递路径分析(OTPA)[4],外源性输入工况路径分析(OPAX)[5],基于部件的TPA(Component- based TPA)[6], 高 级 传 递 路 径 分 析(Advanced TPA)[7]。这些方法是由特定案例推导出来的,因此,不同的TPA技术有各自的适应性与特点。经典TPA技术的被动测频响函数是通过冲击试验和在接受点布置加速度传感器来计算的,不足之处是需要拆解主动部分。TPA的工作流程分为:对活动部件进行操作测试;确定系统的特征;计算界面结合;分析路径贡献量[8]。其特点是计算结果相对准确,但实验过程繁琐。OTPA技术无需分解系统的主动端与被动段,传递函数是基于响应-响应的传递率矩阵计算的[9-11]。其技术特点是实验过程简单,传递率矩阵要求不同工况的响应不相关,否则会影响传递矩阵的精度;而系统模态也会传递路径的相互干扰。OPAX 方法充分利用运行工况数据,增加一组测试来识别运行中的操作力,无需动态刚度的测试与操作力的测试[12-13]。所以OPAX在计算精度与测试时间之间提供了一个折中的方案,并且具有经典TPA 的高精度与OTPA 的高效率。基于部件的TPA 更适合于子结构是关键部件的情况,其主动系统通过专业测试来表现,被动系统可以被数值模拟[14],该方法更适合于用已知实验数据去进行新产品的研发。高级传递路径分析技术(ATPA)与经典TPA 相比,都可以分析各个路径的贡献量,但是TPA 无法描述输入和输出是如何相连接的,而ATPA能够描述输入和输出的关系,从而分析出机械系统的固有结构与传递路径[15-16]。因此,当需要对机械系统进行详细的分析时,使用TPA是有效的方法。
研究离心泵振动传递路径对于有效降低泵的振动能量,实现船舶装备低噪声设计具有重要的现实意义。为了研究离心泵基座的振动来源,对离心泵的振动传递路径进行分析。离心泵结构紧凑但存在多个振动源,这样会引起传递路径重合的问题,致使无法识别振动源的贡献量。为了计算各个路径对目标点的贡献量,提出了一种解决传递路径重合的计算方法。该方法计算了重合路径参考点的净响应,然后采用逆矩阵法计算出各个路径的激励力,提高了载荷识别精度,计算了传递路径的贡献量。最后通过某离心泵的试验结果验证了改进方法的正确性。
1 传递路径分析理论
1.1 传统TPA
经典TPA 的典型模型如图1 所示。该模型将测试点分为参考点、激励点与目标点。在离心泵的振动源识别中,振动源附近的点为激励点,所感兴趣的点为目标点。参考点的选取与激励点的布置有关。逆矩阵法的计算过程为:利用参考点的工况数据计算载荷;将各个载荷与传递函数相乘并叠加得到目标点的计算值;将目标点的计算值与测试值进行对比验证模型正确性;最后进行路径贡献量分析。
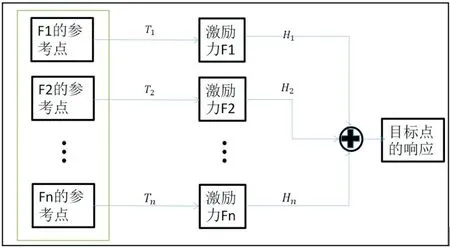
图1 TPA计算流程图Fig.1 TPA calculation flow chart
对于多输入单输出的系统,系统存在单个目标点多个激励源,目标点的响应为多个激励源通过不同的传递路径的叠加:

其中,Y 为目标点的输出;X 为激励点的输入;Hn为激励点到目标点的传递函数。
结构传递路径分析中常采用的激励力识别方法有:直接测量法、矩阵求逆法、动态复刚度法、单路径求逆法和激励点反演法等。其中逆矩阵方法计算精度高,可实行度高,因此工程上常采用此种方法来获取激励力。为了减小病态方程组带了的问题,参考点的个数必须大于激励点个数的2 倍才可以准确计算出激励力。

其中,Fn表示激励点n 所产生的激励力;Cm表示参考点的响应;Tnm表示激励点n与参考点m的传递函数。
1.2 传递路径重合的解耦方法
传统的计算方法是一个振动源对应一个传递路径或者多个传递路径,当有一个振动源使用该路径时,则该路径被占用,即不允许多个振动源共用同一个路径的情况。当一条路径中存在两个及以上的振动源时,必定会引起振动耦合,进而导致目标点的计算值与测量值相差较大,不能准确地进行贡献量分析。为了解决这个问题,提出了传递路径重合的解耦方法,能准确地计算重合路径上的振动源激励力,更加准确地分析各个路径的贡献量。

图2 路径重合问题的示意图Fig.2 Schematic diagram of path overlap problem
图2 中,假设振动源1 与振动源2~r 路径存在部分重合。振动源1的振动会传递到振动源2~r上,这样会引起振动源2~r的振动量增大或者减小,此时的振动源2~r 的信号中混杂着部分振动源1 的信号,最后导致振动源1~r的准确贡献量无法分析。
振动源的激励力是通过其周围的参考点响应间接计算出来的,当路径存在重合时,振动源1 的响应会影响到振动源2~r 周围的参考点,即振动源2~r 周围的参考点的响应中包含振动源1引起的响应,所以想要准确计算振动源2~r的激励力,应该将参考点信号排除振动源1所引起干扰。


图3 振动解耦过程示意图Fig.3 Schematic diagram of vibration decoupling process

我们定义F1RTHr为系统的重叠响应,所以目标点的响应为各个路径响应值的和减去其系统的重叠响应之和。
2 试验验证与研究
2.1 试验描述
泵体的基座振动量过大时会将振动传递到船舶上引起剧烈振动,严重时会导致安装松动,噪声值急剧升高,影响其正常的使用功能及其船舶的隐蔽性。离心泵的基座的振动是由三个振动源引起的,分别是:
滚动轴承为振动源:转子的不平衡、转子的初始弯曲或者轴承的故障都会导致滚动轴承处的异常振动;
蜗壳为振动源:离心泵叶片高速旋转将水流甩向蜗壳,由于蜗壳壁面与叶轮转轴的距离不同,会引起流体的非定常流动,进而引起蜗壳处剧烈振动;
电机为振动源:电机电磁方面的不匹配和机械方面的不平衡(转子的不平衡、联轴器的松动)都会造成电机的剧烈振动。
其中,Path1:电机与基座的振动传递路径;Path2:滚动轴承与基座的振动传递路径;Path2 与Path3:流体激励与基座的振动传递路径。

图4 离心泵振动传递路径示意图Fig.4 Centrifugal pump vibration transmission path diagram

图5 离心泵的结构图Fig.5 Structure diagram of centrifugal pump
离心泵的振动传递路径存在部分重合,流体激励引起的振动会通过滚动轴承处的壳体传递到目标点(基座),即路径流体激励-基座与路径滚动轴承-基座存在部分重合。流体激励的振动会致使滚动轴承处的振动量改变,导致目标点的测试值与计算值相差较大,无法分析各个路径的振动贡献量。

图6 试验现场测试图Fig.6 Test field drawing
关于测点的布置,考虑到离心泵的振动存在三个激励点,每个激励点需要考虑两个振动方向,共有6 条传递路径。所以分别在电机、轴承、蜗壳和基座处布置两个加速度传感器测试其X,Z方向的振动响应。为了保证计算激励力的正确性,参考点布置应靠近激励点并且要保证参考点的数量不少于激励点数量的二倍,所以我们在三个激励源附近分别粘贴了3 个加速度传感器作为参考点的输出。
2.2 试验对比
应用传递路径重合的计算方法对测试得到的数据进行处理。试验设定在电机转速在3 000r/min 的工况下,计算合成的基座位置加速度作为输出信号。将传统TPA 模型合成的输出信号、改进后的TPA 模型合成的输出信号与实测的输出信号三者进行对比,结果如图7所示。
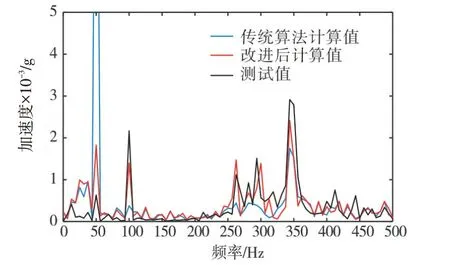
图7 基座测试值与计算值对比图Fig.7 Contrast image of the measured and calculated values of foundation bed
由图7可知,改进后的TPA模型输出信号与实际测试值的吻合度大大高于传统TPA 与测试值的吻合度。在特征频率50Hz、100Hz、262Hz 与300Hz 处,传统TPA计算值与测试值的拟合程度很差,而改进TPA 计算值在特征频率下与测试值拟合程度好,验证了改进后方法的科学性。在改进后的TPA模型中又存在一部分问题:在一些频率段仍然存在一定的误差,误差的原因是TPA 模型的简化振动噪声造成的,详细来说:由于测试条件有限,导致系统输入的测试信号与真实信号存在部分误差;传递路径中存在橡胶垫等非线性材料,其阻尼特性是非线性的,而传递函数在计算时是按照线性系统处理的,所以在分析中无法考虑其非线性阻尼特性。
2.3 试验验证
使用传递路径重合的计算方法可计算出各个路径在不同频率下的贡献量,各个路径的振动贡献频谱图如图8所示。
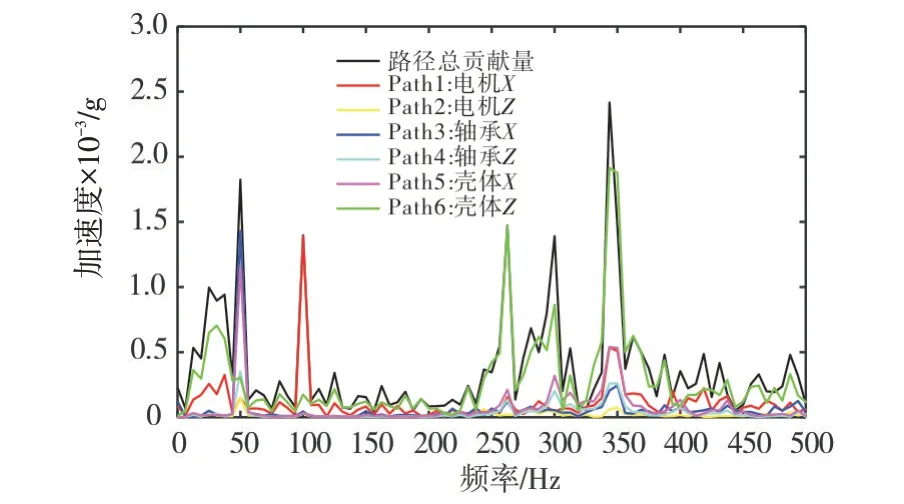
图8 各个路径的贡献量图Fig.8 The contribution diagram for each path
由图8 可知,总体来看,壳体的Z 向在频率段200~500Hz对离心泵的基座贡献量占主导地位,是引起基座剧烈振动的主要原因。在频率50Hz 处,轴承的X 向贡献量最大,在频率100Hz处,电机的X向贡献量最大。
2.4 试验结果
为了更好的分析进行振动源识别与振动原因,对离心泵进行了运行模态测试:

表1 离心泵的运行模态参数Tab.1 Operation mode parameters of centrifugal pump
振动总贡献量的计算不是简单的幅值相加减,而是矢量的计算。为了进一步分析各个路径对几个幅值较大的频率下的贡献量,我们对50Hz,100Hz,262Hz,300Hz,350Hz下的振动矢量图进行了分析。
各个路径的振动矢量在路径总贡献的方向上投影越大代表贡献量越大。由上图可知,在50Hz 处轴承X对目标点贡献量最大,并且其投影值远远大于其他各个路径的投影值。探究其原因,50Hz为轴频,是由于转轴的安装精度不高(转子的初始弯曲)或者制造精度不高(转子不平衡)所致。
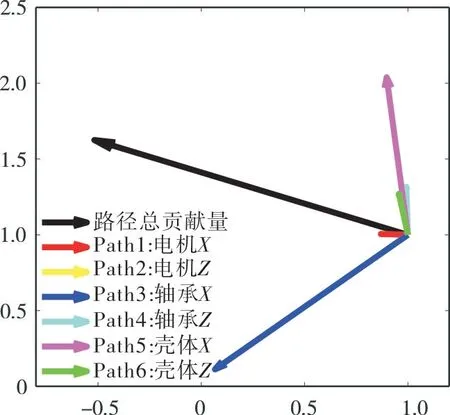
图9 50Hz各个激励源振动矢量图Fig.9 Vibration vector diagram of source in 50Hz
在100Hz处电机X对目标点贡献量最大,并且其投影值远远大于其他各个路径的投影值。探究其原因,定子电机电磁特性是振动频率为电源频率的二倍。壳体Z与轴承X在路径总贡献量方向的投影值较小,即对总贡献量的叠加效果不明显。壳体X 与轴承Z 与总贡献量方向的夹角大于90°,对总贡献量的叠加效果为负值。

图10 100Hz各个激励源振动矢量图Fig.10 Vibration vector diagram of source in 100Hz
在262Hz处壳体Z对目标点的贡献量最大,并且该路径与总贡献量的叠加效果大于路径的总贡献量。轴承X、电机X与总贡献量的振动相位差均大于90°,对总贡献量的叠加效果为负值。探究振动的原因,离心泵的一阶运行模态参数为262Hz,在此频率下,壳体的Z向振动幅度最大,引起了离心泵的共振响应。

图11 262Hz各个激励源振动矢量图Fig.11 Vibration vector diagram of source in 262Hz
在300Hz处壳体Z向与X对目标点的贡献量最大,即在该频率下壳体是引起基座振动的主要振动源。其它路径的对路径总贡献量的叠加效果为零或者为负值。探究其原因,离心泵正常运转时电机转速为3 000r/min,隐藏式叶片有六个,所以300Hz 正好是叶片的通过频率。叶片通过流体的非定常流动将振动传递给壳体,进而壳体通过特定的路径将振动传递到基座上。

图12 300Hz各个激励源振动矢量图Fig.12 Vibration vector diagram of source in 300Hz
在350Hz处壳体Z对目标点的贡献量最大,并且该路径与总贡献量的叠加效果大于路径的总贡献量。其他路径与总贡献量的振动相位差均大于90°,对总贡献量的叠加效果为负值。探究其原因,350Hz可能是由于轴频与叶通频率调频产生的。
3 传递函数与载荷分析
3.1 传递函数
系统的频响函数代表着激励源与目标点的能量传递关系,即表示系统输入与输出的振动传递特性。本文测试中采用了力锤激励法测试了系统输入与输出的传递函数,通过力锤锤击激励点,测试目标点的响应,然后将计算输入与输出的互谱与输入的自谱作比值,计算出其频响函数。
分析图14 可知,轴承Z 向、壳体X 和壳体Z 与基座的频响函数在262Hz附近均在一个较大的峰值,说明在262Hz 处离心泵的下部结构容易引起结构共振。只有当激励频率大于固有频率40%以上时才能起到避免共振的作用,而叶通频率300Hz 正好位于262Hz 的共振带,所以激起了离心泵的共振响应。
3.2 界面载荷力
通过界面载荷力分布图可以清楚地分析出激励力在各个频率下的分布情况,结合界面载荷力分布图与传递函数可以为减振降噪的优化设计提供技术指导。
结合图9 和图15 进行分析,在200~350Hz 处壳体Z方向贡献量值较大的原因是激励载荷的幅值较大,且在350Hz 下存在一个较大的激励载荷,因此可以判断,在200~350Hz 频率段基座振动值偏大的原因是由流体的非定常流动激发壳体的强烈振动,要改善基座的振动必须对流体部分(叶轮、壳体)重新进行参数匹配与优化设计,进而达到减小流体激励降低基座振动量的效果。

图15 壳体Z向(主要振动源)的载荷力Fig.15 The load force in the Z direction of the shell(the main vibration source)
4 结论
针对离心泵振动路径耦合问题,提出了解决传递路径重合问题的解耦方法,得到以下结论:
1)将传统算法和改进算法的计算值与测试值进行对比,发现改进算法的计算值更加贴近真实的测试值,验证了改进算法的正确性。改进后的算法将重合路径上一个振动源参考点作为另一个振动源的目标点,引入了净响应与重叠响应的概念,实现了对传递路径重合问题的解耦,准确地计算出了重合路径上振动源的激励力,为贡献量分析提供了可靠的数据基础。
2)在50Hz 处离心泵基座振动的主要原因是转子的不平衡或者安装精度不高。100Hz 处引起基座振动的主要原因是电机电磁特性所致(定子振动频率为电源频率的二倍)。结合离心泵的振动特性与模态参数,200~500Hz 处引起基座振动的主要振动源是流体的非定常流动。离心泵的第一阶运行模态频率为262Hz,而离心泵的叶通频率为300Hz,容易激起离心泵的共振响应。

