一种构造集合成员表证明集合恒等式的方法

段景辉

(三亚学院信息与智能工程学院,海南三亚 572022)

命题逻辑是以原子命题为基本单位,符号化和形式化地描述人类思维的规律。人类思维的规律是以排中律和矛盾律为基础的规律。排中律思想是二者的选择,只能选择其一,必选择其一,两者不可兼而得之。矛盾律思想是二者的选择,可以兼而得之。

集合恒等式是指集合运算的恒等式,集合运算是集合族上的运算,即以集合为运算对象、以集合为结果的运算。所以集合恒等式本质上就是集合相等问题。集合恒等式的证明,是学习集合论的最基本要求和技能的体现,也是思维方式的一种锻炼[1]。

根据集合对象的确定性,对任何元素a和任何集合A,或者a∈A或者aA,两者必居其一,也只居其一,这条逻辑学中的排中律,再结合命题公式的真值表,本文提出构造集合成员表来证明集合恒等式的方法。

集合恒等式的证明常用方法是:(1)逻辑演算法;(2)集合演算法;(3)集合相等证明法。

1 逻辑演算法

逻辑演算法亦是集合定义证明法。证明思想是从集合运算的逻辑定义出发,设任意元素属于恒等式左边(或右边)集合,根据逻辑演算,等价出恒等式右边(或左边)。

设A、B 为任意集合。

(l)A ∪ B称为A与B的并集,由所有属于A或属于B的元素组成,定义为:

A ∪ B＝｛x|x∈A∨x∈B｝,其中“ ∪ ”称为并运算。因此,x∈A ∪ B ⇔ x∈A∨x∈B。

(2)A ∩ B称为A与B的交集,由属于A同时又属于B的所有元素组成,定义为:

A ∩ B＝｛x|x∈A∧x∈B｝,其中“ ∩ ”称为交运算。因此,x∈A ∩ B ⇔ x∈A∧x∈B。

(3)A-B称为A与B的差集,由属于A而不属于B的所有元素组成,定义为:

例如,吸收律A ∩ (A ∪ B)＝A,A ∪ (A ∩ B)＝A。

证明:对任意x,

x∈A ∩ (A ∪ B) ⇔ x∈A∧x∈(A ∪ B)

⇔ x ∈A

x∈A ∪ (A ∩ B) ⇔ x∈A∨x∈(A ∩ B)

⇔ x∈(A ∩ U)∨x∈(A ∩ B)

⇔ x∈A ∩ (U ∪ B)

⇔ x ∈A ∩ U

⇔ x ∈A

2 集合演算法

集合演算法亦是集合恒等式法。证明思想是从集合恒等式的左边(或右边)开始,利用已知的集合恒等式作等价代换处理,直到集合恒等式的右边(或左边)。有的时候,也需要从恒等式的左右两边同时利用集合恒等式法,等价出中间一个相同的集合。

例如,吸收律A ∩ (A ∪ B)＝A。

表1 集合成员表Tab.1 Set member table

例如,A-(B ∪ C)＝(A-B) ∩ (A-C)。

证明:左边＝A-(B ∪ C)

右边＝(A-B) ∩ (A-C)

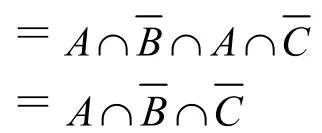
因为:左边=右边。

所以:恒等式成立。

此例证明中,还可由(1)式直接等价演算右边。

例如:对任意集合A、B、C、D,证明 A ⊆ B, A - B=,A ∪ B = B, A ∩ B = A四命题等价。

证明:设4个命题为P、Q、R、S,即证P⇒ Q⇒ R⇒ S⇒ P,从而就证实4个命题等价。

(Q⇒ R):为证A ∪ B＝B,需证

1)B ⊆ A ∪ B。但由定理4.2之(1),此已得证。

2)A ∪ B ⊆ B。设x为A ∪ B中任一元素,从而x∈A或x∈B。当x∈B时目的已达到。当x∈A时,若xB,则x∈A-B,此与A-B＝矛盾。故x∈B。总之,A ∪ B中元素x必为B中元素。

综合1)、2)可知A ∪ B＝B,R得证。

(R⇒ S):因A ∪ B＝B,故A ∩ B＝A ∩ (A ∪ B)＝A(吸收律)。S得证。

(S⇒ P):设A ∩ B＝A。要证A ⊆ B,现设x为A中任一元素。由A ∩ B＝A,可得x∈A ∩ B从而知x∈B。故A ⊆ B,P得证。

注意,上述“循环论证”只是证明若干命题相互等价的方法;在此过程中,那些命题自身一个也没有得到证明。

3 集合相等证明法

集合相等证明法是根据集合相等定义(即外延性原理)进行证明,即A＝B,当且仅当A ⊆ B且B ⊆ A。

景花厂的员工增到了七十多人，仍忙不过来，订单像鹅毛，一片片飞来。王义山对我很敬佩，不时在阿花面前夸我，说我比高文鹏强，技术水平高，质量要求严，还会拉订单。高文鹏就是我的前任。我也礼节性地赞扬王义山，生产才是工厂的生命，你也功不可没，阿花经常表扬你。阿花说，你们是我的左膀右臂，你们合作得好，我就轻松了许多。怎么样，最近人手够吗？王义山说，差不多了，机位快坐满了，车间也显得有点拥挤。我们边说边进了车间。

例如,分配律A ∩ (B ∪ C)＝(A ∩ B) ∪ (A ∩ C)。

证明:为了证明A ∩ (B ∪ C)＝(A ∩ B) ∪ (A ∩ C),只需要证明

A ∩ (B ∪ C) ⊆ (A ∩ B) ∪ (A ∩ C)和(A ∩ B) ∪ (A ∩ C) ⊆ A ∩(B ∪ C)。

首先,设x∈A ∩ (B ∪ C),那么x∈A且x∈B ∪ C。根据集合并集定义,得x∈A且x∈B或x∈C;根据集合交集定义,再利用命题公式的分配律,可得到,x∈A且x∈B或x∈A且x∈C。根据集合交集定义,可得x∈(A ∩ B) ∪ (A ∩ C)。因此,得证A ∩ (B ∪ C) ⊆ (A ∩ B) ∪ (A ∩ C)。

然后,设x∈(A ∩ B) ∪ (A ∩ C),那么x∈A ∩ B或x∈A ∩ C。根据集合交集定义,得x ∈A 且x ∈B或x ∈A 且x ∈C;根据集合并集定义,再结合命题公式的分配律,可得到x ∩ A ∪ (B ∩ C)。因此,得证(A ∩ B) ∪ (A ∩ C) ⊆ A ∩ (B ∪ C)。

综上,A ∩ (B ∪ C) ⊆ (A ∩ B) ∪ (A ∩ C)且(A ∩ B) ∪ (A ∩ C)⊆ A ∩ (B ∪ C),所以A ∩ (B ∪ C)＝(A ∩ B) ∪ (A ∩ C)。

上述三种集合恒等式的证明方法是较为常用的方法,也是学习集合论必须掌握的证明方法。其中,逻辑演算法和集合相等证明法,都是基于集合运算的逻辑定义进行的。由此可以看出,集合运算的恒等式与命题公式的逻辑等价式是非常类似的。所以,在命题公式的真值表的基础,提出了集合恒等式的另一种证明方法——集合成员表法[2]。

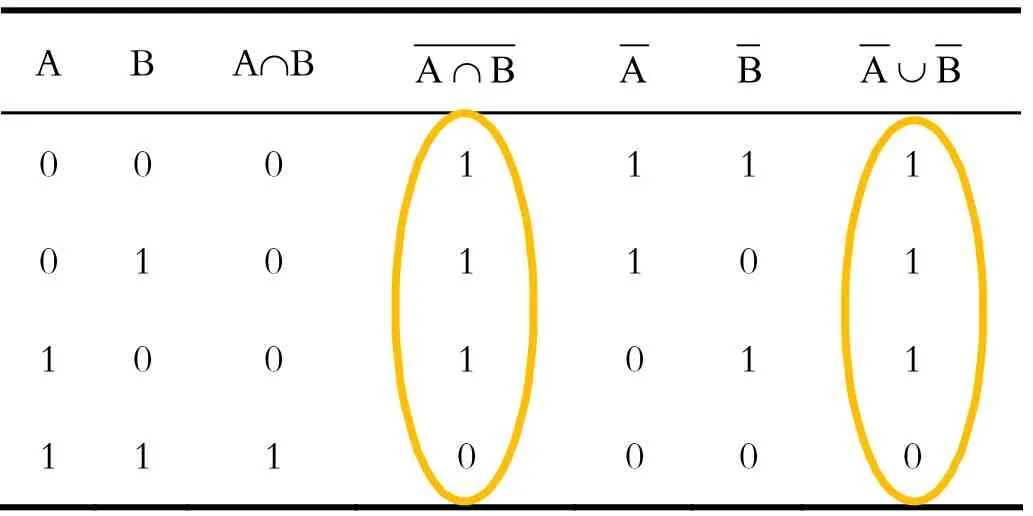
表2 集合成员表Tab.2 Set member table

4 集合成员表法

集合成员表类似命题公式的真值表。

首先, 考虑一个元素可能属于的集合的每一种组合,用1表示元素属于一个集合,用0表示元素不属于一个集合。

其次,再证明在同样的集合组合中的元素属于恒等式两边的集合。

(2)集合成员表法的作法。

首先,确定恒等式中不同集合的个数n,那么成员表就有2n+1行(第1行是表头)。

其次,恒等式两边的表达式分别表示,确定恒等式左边的集合运算符个数m,右边恒等式的集合运算符个数z,那么就有n+m+z列。

(3)举例。

例1:证明分配律A ∩ (B ∪ C)＝(A ∩ B) ∪ (A ∩ C)。

证明:作A ∩ (B ∪ C)＝(A ∩ B) ∪ (A ∩ C)的成员表,如表1所示。

由表1的第五列和第八列可以看出,其值完全一样,所以A ∩ (B ∪ C)＝(A ∩ B) ∪ (A ∩ C)得证。

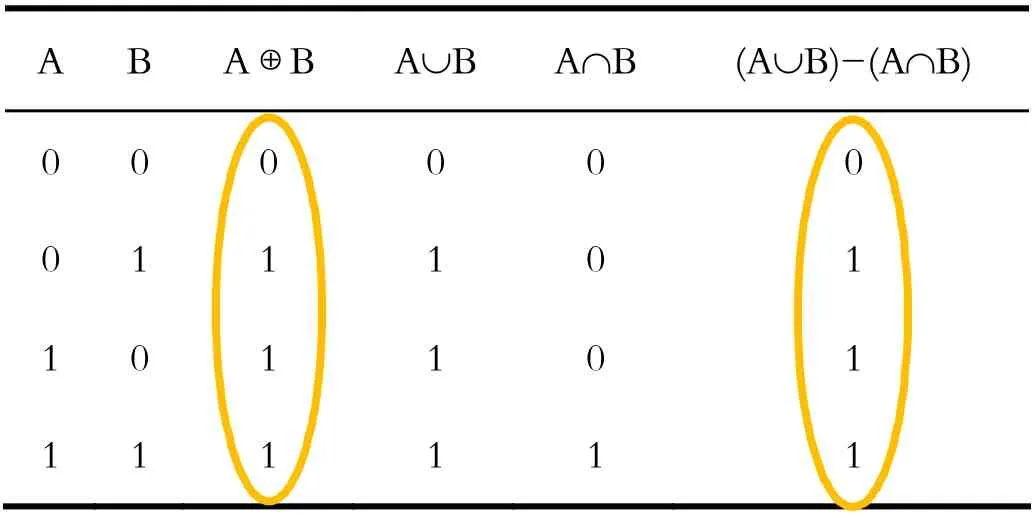
表3 集合成员表Tab.3 Set member table

例3:证明A⊕B＝(A ∪ B)-(A ∩ B)。

证明:作A⊕B＝(A ∪ B)-(A ∩ B)的成员表,如表3所示。

由表3的第三列和第六列可以看出,其值完全一样,所以A⊕B＝(A ∪ B)-(A ∩ B)成立。

5 总结

集合论是一门研究数学基础的学科,集合恒等式是集合论的最基础内容,集合恒等式的证明,是人们拓展集合运算的一种方式,也是人类思维的一种形式体现。

集合恒等式的证明,方法很多,本文的集合成员表法是基于命题公式的真值表而提出的,这种方法形式简单、易于掌握,更重要的是它揭示了集合恒等式与命题公式恒等式之间逻辑特性。

集合成员表证明方法,实质是将命题演算中的排中律、矛盾律运用在集合中,这种方法不仅可以直接证明集合恒等式，还可以体现出逻辑思维。