基于马尔可夫跳变神经网络的采样同步控制研究

田佳萍，谢立典，王春柱，王嘉伟，葛超

（1.华北理工大学人工智能学院，唐山063210；2.石家庄海山实业发展总公司，石家庄050200；

3.火箭军综合训练基地学兵训练一队，唐山064000）

研究马尔可夫模型的神经网络采样控制的主从同步问题。在零输入策略的框架下，提出一种新型的可变采样随机切换采样数据控制器。基于Lyapunov函数方法，构造适当的Lyapunov-Krasovskii函数（LKF）充分利用有关实际采样模式的可用信息。使用凸组合技术和自由权矩阵的积分不等式，得出一些充分条件。通过求解线性矩阵不等式（LMI），可获得相应的采样数据控制器。给出的数值算例说明该方法的有效性和优势。

采样控制；马尔可夫跳变；LMI；神经网络

0 引言

如今，由于神经网络已广泛用于各个领域，例如信号处理、图像处理、模式识别、优化和关联存储设计等，因此，神经网络受到了广泛的关注[1-2]。对于控制界来说，神经网络的吸引力在于它们可以完全近似复杂的非线性映射关系，并且它们可以学习并适应不确定系统的动态特性。以这种形式，将神经网络引入控制系统是控制学科发展的必然趋势。近年来，与神经网络有关的稳定性分析已被深入研究，并获得了很多成就[3-4]。

随着对神经网络问题的研究，神经网络同步控制问题逐渐被发现和广泛研究。神经网络的同步控制处于神经网络的稳定性之下。为了保持主从系统的同步状态，设计了合适的控制器。神经网络的主从同步已逐渐成为必不可少的研究领域。近年来，已经提到了许多重要的主从同步方法，例如脉冲控制[5]、固定控制[6]、输出反馈控制[7]、自适应控制[8]和采样数据控制[9]。

得益于计算机技术的进步和对其的深入研究，在过去的几十年中，采样数据控制系统引起了越来越多的兴趣。一些文献[10-11]报告了许多基本结果。为了同步，被采样的数据仅需要关于采样时刻的系统状态的信息，其方法的特点是减少了传输的信息并提高了控制效率。使用采样数据控制实现神经网络同步时，选择采样周期是一个重要的问题。更长的采样间隔将带来更低的通信信道占用，更少的信号传输以及更少的驱动控制器信号[12-13]。采用了一种新的LKF和线性矩阵不等式（LMI）技术来研究动态网络采样数据的同步控制。因此，设计具有更长采样周期的同步控制器尤为重要。

在另一个研究前沿，众所周知，马尔可夫跳跃系统是一种有限模式操作的特殊动力学系统，由于其在许多动力学模型中的潜在应用，在过去的几十年中一直引起越来越多的研究关注[14]。在文献[15]中研究了具有输入振幅约束的不确定Markovian跳跃神经网络的有限时间同步控制。文献[16]研究了具有时变间隔和时滞的Markovian跳跃广义神经网络的耗散稳定性分析问题。总结已有文献，对采样数据神经网络系统的马尔可夫跳跃研究具有重要意义。

1 模型建立和问题描述

1.1 基于丢包的神经网络采样的同步控制系统的模型构建

我们构建的神经网络模型如下：

其 中 x(t)=[x1(t)，x2(t)，…，xn(t)]T表 示 状 态 向 量。A=diag{a1，a2，…，an}表示的正定对角矩阵，其中Ai＞0；B=(bij)n×n表示连续的权重矩阵；J(t)=[J1(t)，…，Jn(t)]T为常数的输入向量；g(x(t))=[g1(x1(t))，g2(x2(t))，…，gn(xn(t))]T表示神经元的激活函数。

假设g(∙):Rnh→Rnh是属于扇区[σ-i，σ+i]，i=1，2，…，nh的非线性函数。也就是说，非线性函数g(∙)满足以下条件[29]：

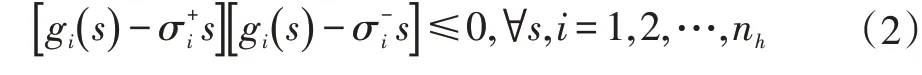
在完全概率空间中，我们设{r(t)，t≥0}是一个右连续Markov链。它描述了t时间模式的演化，取有限状 态 空 间G={1，2，…，N}中 的 值，其 生 成 元γ=(γij)，( i ，j∈G)由下式给出：

结合上述，具有马尔可夫跳变的神经网络主系统被表示为：

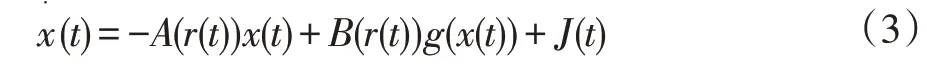
对应的从系统表示为下列形式：

其中，u(t)=Ke(tk)表示基于采样时刻tk的控制输出，K为待求解采样数据控制器的增益矩阵。

结合上述主从系统，令e(t)=y(t)-x(t)，可以得到如下的误差系统：

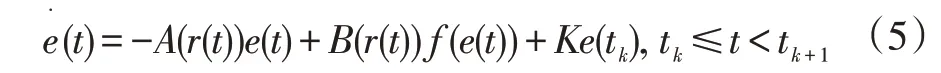
当s∈R且s≠0时，函数fi(s)满足以下条件：

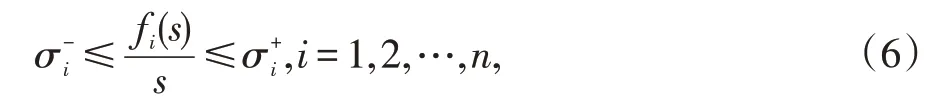
1.2 相关定义和引理

2 定理

在这部分，我们将找到一种方法求解控制器矩阵K。为了简化矩阵表达式，我们给出以下定义：

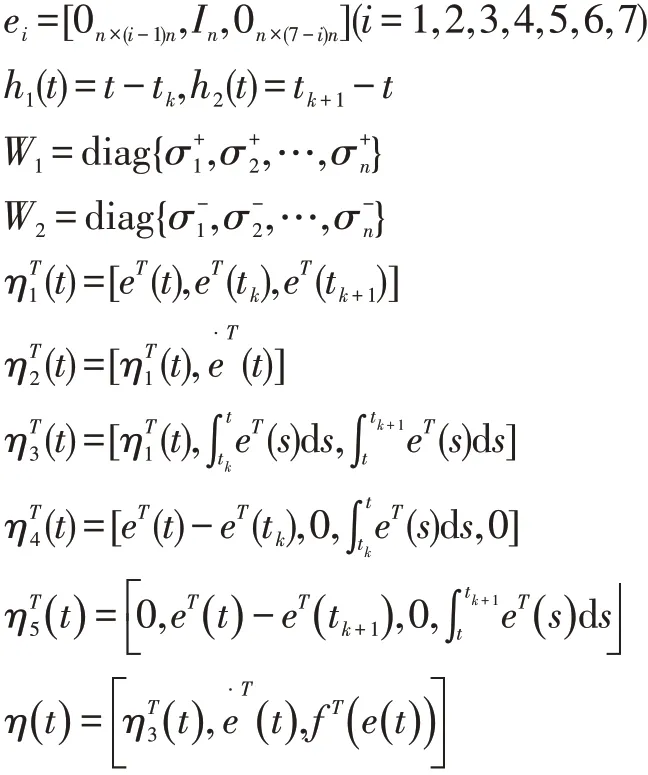
对于给出的参数值h＞0，ϵ1＞0，ϵ2＞0，误差系统

图1 神经网络主从系统的状态反应

利用得到的上述增益K，控制器u(t)的对应关系如图2所示，误差状态e(t)如图3所示。由图3可知，状态变量的变化趋势最终趋近于0，这也验证了我们方法的有效性和可行性。

图2输出控制曲线u（t）

图3 含有控制输入的误差系统的状态响应

4 结语

在本文中，我们提出了一种新的马尔可夫跳跃神经网络的随机切换采样数据控制方案。通过零输入法的框架，伯努利分布模型已用于建模。与相关文献相比，马尔可夫过程更为通用和实用。为了充分利用各种可用信息，构造了一个新的增强LKF来分析相应的错误系统。基于Wirtinger不等式，获得了一些较不保守的条件来保证主从系统的同步。此外，可以通过求解LMI来合成采样数据控制器增益矩阵，该矩阵取决于最大允许的采样周期。最后，一个数值算例表明了该方法的有效性和优点。