基于PI算法的自适应天线阵仿真研究
王雨,林浩冬,李成,肖成坤,徐开俊
(中国民用航空飞行学院,广汉618300)
自适应调零天线技术能够在干扰信号方向产生零陷,以抑制干扰信号,有效地改善卫星导航接收机的抗干扰性能。在分析功率倒置自适应算法原理的基础上,基于LMS算法完成四元方形阵和四元Y形阵的抗干扰仿真,验证自适应天线阵的抗干扰性能,为后续研究工作提供基础。
卫星导航;PI算法;抗干扰
0 引言
现代导航系统能够给个人、车辆、飞机等提供实时的位置和导航信息,现代军事战备设施、不同的武器平台同样需要这些实时的位置和导航信息。因此,导航系统在现代社会的应用越来越广泛[1]。但是鉴于导航卫星它在空中受条件的约束,发射功率相对较低,并且导航信号是对社会公开其发射频率的,所以导航接收机是容易被外界干扰的,导致不能正常地提供导航服务。
现代卫星导航系统的体系已经发展的很成熟了,一方面其结构也早已被公开研究,另一方面卫星的信号频段是对大众公开的,所以卫星导航系统十分容易被不法分子进行恶意的干扰。以GPS系统为例,它是技术上最为成熟且被大众所高度使用的卫星导航系统,其卫星的轨道和地面之间大约有着2万多千米的距离,又因为卫星本身的发射信号的功率不大,再经过长距离的传输后,当信号被接收机接收时有时只能够达到-130dBm。当地面的接收机受到了外部的强的干扰时,此时GPS接收机已经不能完成捕获跟踪等一系列工作了。有资料显示,功率为l0W的干扰机可以使88km范围内的接收机失效[2]。鉴于以上的问题,研究抗干扰技术对各国而言是非常重要的一项任务。除此以外,对GPS系统的抗干扰研究所学习和了解的知识,一方面能够对我国的北斗卫星导航系统的研究有着参考作用,另一方面对于如何对GPS接收进行有效的外部的干扰也有很强的指导作用。
世界各个国家已经研发出了很多的抗干扰技术来达到提高接收机抗干扰性能的目的,以此避免外界干扰危害。而在这许多的技术中,不得不提的就是自适应调零天线技术,由于它在抗干扰方面的行之有效,因此这种技术早已被大范围的应用在军方及民用的GPS接收机和现代武器系统中。
本文不仅讲述了自适应调零天线的技术原理和功率倒置算法的技术特性,并通过信号仿真实现了四元方型阵和Y型阵两种不同阵列对单源、双源、三源干扰信号的干扰抑制,为自适应调零抗干扰天线的进一步研究与应用提供支撑。
1 自适应调零天线技术原理
自适应调零天线技术是一种在空域上的自动的抗干扰的技术,通常是由几个单元来组成阵列,各个天线阵元再将准备发出的信号进行复数加权,再通过叠加之后,一方面输出,再经过处理使得整个天线阵列的信号功率达到最小值,在不同的天线阵元上的加权值不同,以此就能够在相应的干扰信号的方向上形成对应的零陷。
自适应阵列处理选择使用阵列天线而不是单个的天线来进行接收信号,主要是由两种搭配结合成的,自适应信号处理技术与阵列天线相结合,能够很容易地对方向图进行控制,从而抑制干扰。并且阵列天线可以在空域、空时域或空频域对阵列的接收信号进行处理,而单个天线的方向图则是由其形状所固定,没有办法随着环境改变。
除此之外,自适应天线阵列还能够依据信号和干扰的入射方向所发生的变化,来调整整个天线阵列的空域滤波特性,实现对干扰的抑制。自适应调零天线的结构原理如图1所示。
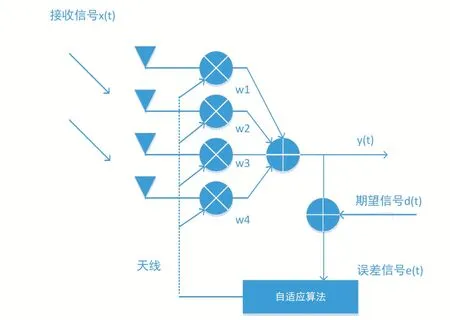
图1 自适应调零天线框图
令xi(n)代表i路的天线所接收到的信号,令wi表示在i路天线上的权值,因此所接受信号Χ(n)的公式如下:

令不同的天线的权值用公式表示如下:

由此天线阵的输出为:

自适应阵列其主要的目的是计算出最优的加权矢量,然后根据这个加权矢量才可以在各个通道上加权处理以此实现干扰抑制,通过调节加权矢量,让天线阵在特定的干扰方向的输出功率达到最小。
2 基于LMS算法的自适应调零技术
在空域自适应算法中,比较常见的有最小均方误差(LMS)算法、约束自适应算法、递推最小二乘(RLS)算法、采样矩阵求逆(SMI)算法以及Howells-Apple⁃baum(HA)算法等[3]。LMS是非常经典且简单、有效的一种算法,广泛的在各种工程和科学研究中使用。
在自适应天线阵列中,天线单元负责耦合空间电磁信号,由于载体大小的限制,不能使用过多天线单元[4]。只能在条件允许的情况下,尽量选用最多的天线单元。本文根据实际情况选用4个天线单元来构成天线阵列。对于四元阵列天线,典型的阵元布局有正四边形分布和Y型分布两种布局,示意图如图2所示。

图2 四元方形阵与Y形阵布局图
在LMS算法中,首先选定一个阵元,把该阵元的信号假设为我们所需要的参考信号,之后再依次对别的阵元的权值解算,最终使得参考信号与整个阵列的输出二者之间的均方误差能够达到最小。
设权系数:

信号:
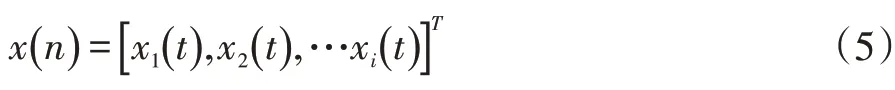
期望输出为d(n),由定义当前的阵列输出为:

阵列的输出误差可以表示为:

因此问题能够等效成求解能够使得ξ=E[e2(n)]达到最小的系数向量wopt。
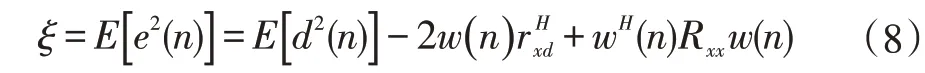
在上式中,Rxx是接收的信号向量的自相关矩阵,rxd为信号和期望响应之间的互相关向量。计算之后得到wopt:

LMS算法非常简单实用是因为它在计算最佳权矢量时,并不是采用矩阵求逆的方法来得出的,而是采用了对梯度进行估计的方法。
若w(n)的梯度∇wξ是我们已经知道的,w(n)就可以推出如下的方程:

μ是一个实数参数,又叫做步长参数,它将影响算法中权矢量w的更新速度以及算法最终的稳定度[5]。
这在算法的计算过程中,设定w的初始值,ξ沿着梯度下降。使ξ趋于最小值的w(n)就是最优解。其迭代公式可以表示为:
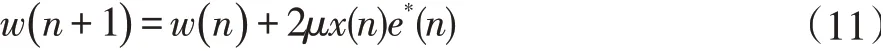
最后经过多次的迭代计算后就解出了最优权值wopt=R-xx1rxd。得到了wopt以后,再对几个单元的权值来调整,也就是达到干扰抑制的目的。
3 自适应调零算法仿真
本文使用MATLAB软件进行编写程序,对LMS算法仿真,本次仿真选择四元阵列,对于四元阵列天线,典型的阵元布局有正四边形分布和Y型分布两种布局。
为了尽量避免盲相,选择设置阵元的间距为0.5λ。在噪声方面我们选择高斯白噪声来进行实验。由仿真的结果,对两种不同的阵列面对相同的干扰时其抑制效果进行一个分析。
选用单个干扰信号,设置入射的俯仰角为40°,方位角为50°,仿真结果得到的方向图如图3、图4所示。
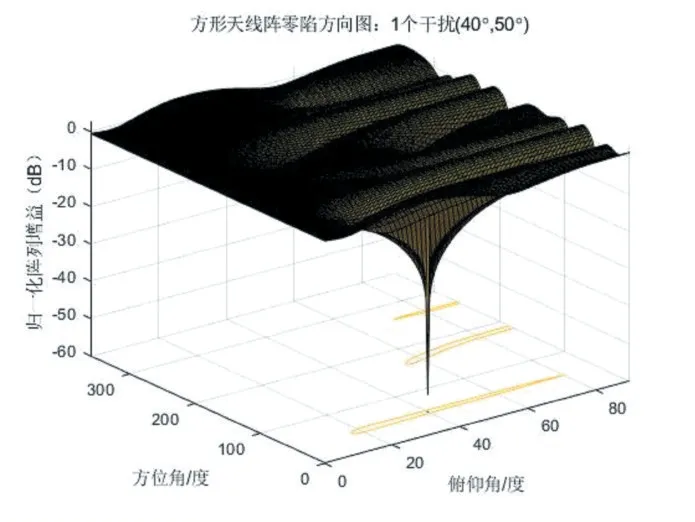
图3 四元方形阵对单个干扰的抑制结果
通过上图进行分析可以得出结论,在俯仰角为40°,方位角为50°的方向上,这两种天线阵列都形成了零陷。对两张仿真图对比能够发现,四元方形阵列在方向图上的零陷的形状是非常不规则的,而且它在较大的俯仰角度范围内都有一定程度的抑制,这就很有可能对有用的卫星信号形成了抑制。相反,可以看到四元Y形阵列就没有出现这种情况,它所形成的零陷形状在俯仰方向所形成的零陷宽度相对较窄,并不会出现对有用卫星信号抑制的情况。出现这种状况的原因是Y形阵它的参考阵元是处于整个阵列的中心位置,另外的三个阵元则分布在中心的四周,所以相对而言就不容易产生测向模糊。因此相较于对于四元方形阵列来说,四元Y形阵列的抑制性能较好。
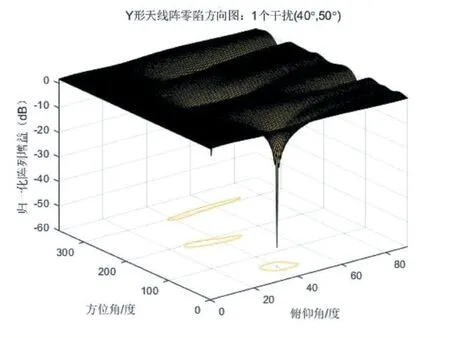
图4 四元Y形阵对单个干扰的抑制结果
选用两个干扰信号,分别对其设置为俯仰角为40°,方位角为50°与俯仰角为20°,方位角为200°,其仿真结果如图5、图6所示,由图可看出,选择的两种天线阵列都在设定的干扰方向上得到了期望的零陷。

图5 四元方形阵对双源干扰的抑制结果
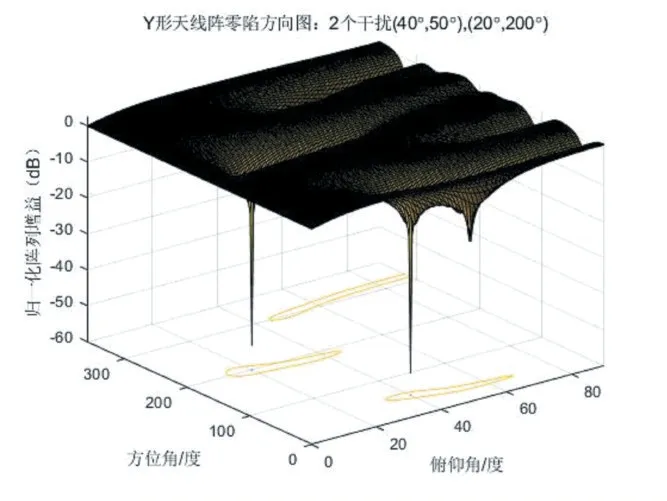
图6 四元Y形阵对双源干扰的抑制结果
选用三个干扰信号,对其分别进行设置,为俯仰角为40°,方位角为50°与俯仰角为20°,方位角为200°,和俯仰角为10°,方位角为280°。其仿真的结果方向图如图7、图8所示。由图可看出,在这三个方向上都形成了零陷,但由于四元阵列的抗干扰自由度已经全部占用,在某些非干扰方向也形成了抑制,可能对正常信号的接收带来一定的负面影响。这是因为在此时干扰个数已经超过了选定的天线阵列的自由度了,导致不能够像预期一样形成零陷,也就无法实现抑制干扰的功能。
根据以上对两种阵列所进行的仿真实验,可以得出结论,基于功率倒置算法的自适应调零天线能够对单源、双源干扰、三源干扰的环境下都能够对干扰信号实现抑制功能,非常适用于卫星导航接收机,能够对卫星导航的正常运行提供保护。
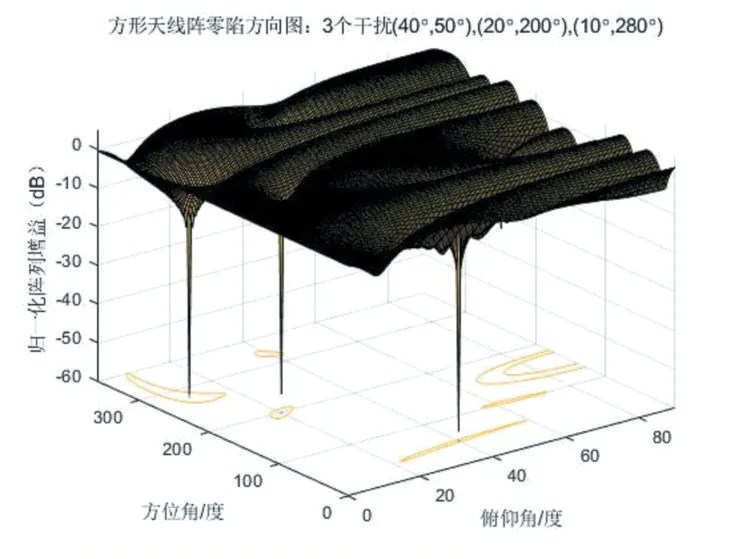
图7 四元方形阵对三源干扰的抑制结果
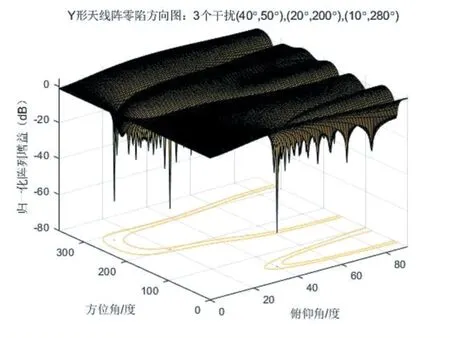
图8 四元Y形阵对三源干扰的抑制结果
4 结语
本文重点分析与研究了基于功率倒置的自适应调零天线抗干扰技术,使用LMS算法来求解最优权值并且对它的迭代过程进行分析。使用两种经典的天线阵列对单源、双源、三源干扰分别进行了仿真实验,通过仿真成功实现了自适应调零天线技术对干扰信号的抑制功能,在此基础上对不同布局的阵列的抗干扰性能进行了简要的对比和分析。本文的研究为后续进一步功率倒置自适应调零技术的研究应用提供了基础。

