到底什么样的课堂活动才是真实的

丁翠萍

点评：恩施市教学研究和教师培训中心  柳兴平

内容：人教版六年级上册《扇形统计图》例1。

教学目标：

扇形统计图的特点和作用是什么（即教学重点）？

实际生活中为什么要使用扇形统计图（即教学难点）？

能联系百分数的意义，对扇形统计图提供的信息进行简单的分析。

师：下面是某校三（6）班同学参加课外兴趣小组的一些信息得出的统计表，请根据这张统计表，回答这样的一个问题：“你能算出喜欢每种运动的人数各占全班人数的百分之多少吗？”

当学生顺利完成以上这个问题之后，教材便急转直下并直截了当地这样表述：“我们可以用扇形统计图来表示各部分数量与总量之间的关系”。

师：对教材上说的这句话，同学们是怎样理解的呢？请先独立思考，然后举手发言。

学生1：“可以用扇形统计图”是不是还可以理解成“也可以不用扇形统计图”呢？

学生2：是啊，不用扇形统计图的话，该用什么样的统计图呢？

学生3：扇形统计图，扇形统计图到底是哪个样子的啊？

师：大家还有要说的吗？没有了。那就请同学们用一幅图清晰地表示出各小组人数与总人数之间的关系，你想怎么画就怎么画，画好之后先在小组内交流交流，然后将你们的作品展示给全班同学。

评析：教师是课堂教学中的组织者、引导者与合作者，这既是一种教育理念也是一种教学方法。如何与教材对话，如何深挖教材，丁老师只是很自然地提出了一个问题，带着这个问题让同学们自己去思考，老师也没有生搬硬套地用教材上的原话强行向学生灌输，老师仅仅是起到一个引导者的作用，师生间处于平等的地位，是一种合作者的关系。丁老师对教材中“我们可以用扇形统计图来表示各部分数量与总量之间的关系”这句话的解读与处理非常恰当，通过三个学生的发言，便将隐藏在这句话背后的问题全部挖了出来，且均由学生们自己思考完成。丁老师的一句“对教材上说的这句话，同学们是怎样理解的呢？”仅仅是提醒学生思考，没有帮一点点小忙，全部由学生自己思考解決，且这样解决的基础完全符合学生已有的认知。这样的活动显然是真实的，是极其有效的。

五分钟左右之后，大部分小组都交流讨论完成了。丁老师便将两个小组的作品用手机拍下后直接传到了电子白板上（如下图）。

当全班同学仔细观察完这两幅作品之后，丁老师便请这两个小组的学生代表来解释解释。

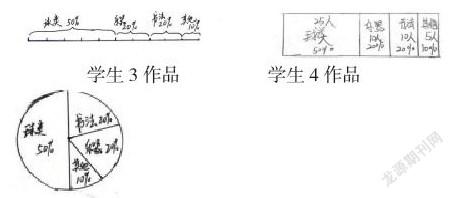
作品1学生代表：我们画的是条形统计图，可以非常直观地看出哪个小组的人数多哪个小组的人数少。但要看出各小组的人数占全班人数的百分比的问题，还是不清楚明了。同时，刚才我们才发现，图中的统计单位不应当是“百分号”，而应该是“人数”才正确。

作品2学生代表：我们画的是折线统计图，这个图能清楚地看出参加兴趣小组的人数是越来越少。

师：同学们，刚才这两位同学说的观点大家赞成吗？

一位男生迅速举起手说道：“第一个的我赞成，但第二个的这样说不对。如果在列统计表的时候，把这些兴趣项目的顺序调整一下，画出来的图形就不是越来越向下的呀，也就是说不一定是越来越少啊。”

师：说得好，大家听清楚了吗？请大家再认真思考思考，用这样的折线统计图能清楚地反映出各小组人数占全班人数的百分比吗？

生：不行不行（几乎是异口同声）。

师：好的，下面我们再看几幅作品，请大家仔细观察观察，然后听听他们是怎样解释的哟。

作品3的代表说：“我们是把全班人数看作一条线段，并把这条线段平均分成10份，由于喜欢“球类”的人数占全班人数的百分之五十，因此，在这条线段中它占一半的位置，喜欢“乐器”和“书法”的人数各占百分之二十，也就是共占四条小线段，“其它”的占百分之十，也就是占一条小线段。”

作品4的代表说：“我们把全班人数看作一个长方形，喜欢“球类”的人数占全班人数的百分之五十，我们就取这个长方形的一半，……”作品5的学生也作了类似的说明。显然，这三幅作品都能清清楚楚一目了然地表示出各小组人数与总人数的关系，也就说，这三幅作品都抓住扇形统计图最基本的特征了。通过这三位同学的讲解，那些原来未弄明白的同学绝大部分都搞清楚了。

评析：当我们为这三幅作品进行点赞的同时，仔细分析他们的思路，其实他们仍然是用旧知在解决问题。所用的旧知就是本学期刚刚学过的百分数和在五年级学习分数时认识的单位“1”。在这三幅作品中，都是把全班总人数看作一个计量单位“1”，这个单位“1”用符号或图形表示，可用长度单位的线段图形，可用面积单位的平面图形，如长方形正方形或者圆，还可以用体积单位的立体图形，如长方体正方体或者圆柱甚至一个球体。只要能反映出扇形统计图的本质意义，无论采用哪种图形都是可以的。这样的动脑又动手的课堂活动，无疑是真实的有效的。

师：同学们，既然以上三幅作品都能反映出各小组人数与总人数的关系，那么，你觉得哪幅作品最简洁明了呢？请先独立思考，然后在小组内讨论。

小组1：线段图和长方形（或正方形）虽能体现部分与整体的关系，但不是最直观的，特别是这个整体“1”一眼难以看出，最直观的还是扇形图，一看就清楚。而且画图时正方体或长方体虽然能体现出部分与整体的关系，但画图时比较复杂麻烦，不是很简洁。

小组2：在将单位“1”这样的图形进行平均分的时候，作品3中的线段图虽然画起来比较简单，但观察时不是非常明了，一目了然就能看出来的还是作品5，也就是扇形统计图。而立体的图形更不好操作。

师：的确，用圆来表示整体有着得天独厚的优势（同时出示下面图片）。

对比这两幅图，都将百分之十的“其它”项目少掉了，显然从线段图中很难一眼就能看得出来，而扇形统计图少了的这一块，立马就能看出来，所以用扇形统计图来表示部分数量与总数的关系是最直观的，也是最清晰的。。

评析：一节课进行到这个时候，可以说三个目标中的前两个已经顺利得到完成。为什么要使用扇形统计图以及扇形统计图的特点是怎样的，都是学生们自己思考、动手操作和充分讨论后得出的结论。

总评：上面的五幅作品，基本上就代表了全班同学解决这个问题的整体情况。我们要追问的是，学生们为什么会这样去想呢？其实就是老生常谈的一句话，符合认知规律，即从旧知到新知。学生作品1和作品2虽然不正确，但是他们的思考过程是很真实的，因为在这之前学生学过且仅仅学过两种统计图，即条形统计图和折线统计图。用这两种统计图来解决新的问题，是完全符合学生的认知规律的。当用所学的旧知画出新的统计图之后，发现不能完全解决老师刚刚提出的这个问题时（能一目了然地看出部分与整体的关系吗？），从而激发出学习研究的兴趣。这些学生将带着这个疑问在观察后面三幅作品的展示交流中得到有效解决。

我们常说，要让课堂真实起来，不要做作，不要花里胡哨。其实，要使课堂真实也很简单，一是学生的思维过程要真实，思考路径符合他们的认知规律;二是动手操作要真实，凡能自己动手的都必须亲自动手。像上面丁老师展示的这节课就是非常真实的课。这样的课学生学得轻松学得愉快，是有趣的，也是很有效的。