基于遗传-粒子群混合优化算法的拆卸序列规划方法研究*
王玉鑫,任 帅
(中国民航大学 航空工程学院,天津 300300)
0 引 言
为确保使产品具有良好的维修性,并且保证新产品在投入运营后,可以正确地使用和维修,制造商应开发并提供正确、合理、详尽、便于使用的新产品运行文件,后勤保障分析国际程序规范(S3000L)明确要求产品在设计阶段应该考虑在运营阶段和报废阶段的拆解,这要求在技术出版物中必须有相关拆解流程,即需要进行拆卸序列规划(disassembly sequence planning,DSP)。
进行拆卸序列规划在设计阶段有助于提高产品的维修性,且可对技术出版物进行有效验证;在运营阶段或报废阶段也可以有效地在工程中提高工作效率,降低维修成本。
拆卸序列规划的目的是生成零件或者部件的拆卸顺序,以使得在维修工作中达到决策者的“最佳目标”,此最佳目标一般指拆卸成本最小、拆卸收益最大、对环境污染最小等要求,其好坏程度对于产品维修活动的有效性和经济性有着直接的影响[1]。
DSP问题本质上可以抽象为一个排列组合的优化问题,随着产品零件数量的增加,拆卸序列的数量会呈指数型增长,即组合爆炸现象[2]。因此,DSP问题的求解将会是DSP问题的关键。对此,国内外大量学者对其进行了深入研究,比如蚁群算法[3-5]、人工蜂群算法[6,7]、遗传蝙蝠算法[8]等。
蚁群算法经改进后具有良好的收敛性;人工蜂群算法起步较晚,在该问题的应用也较少,其同样可在保证种群多样性的前提下实现算法的快速收敛;虽鲜有人将蝙蝠算法用于拆卸序列规划问题,但经改进的遗传蝙蝠算法的收敛性和收敛速度也优于遗传算法(GA)。TSENG Y J[9]等提出了一种基于粒子群算法(PSO)的闭环装配与拆卸序列规划的绿色装配序列规划模型,但是未考虑在通过粒子群迭代后的序列优先关系;同样地,张秀芬[10]在通过粒子群算法对拆卸序列进行寻优中也未考虑新一代的序列是否满足拆卸优先约束;在后续研究中,张济涛等[11]提出了基于量子遗传算法的拆卸序列规划模型,对该问题进行改进,其结论为迭代次数减少,可较快得出最优解;然而其方法在每次迭代之后对所得出序列进行检验,若序列满足优先约束,则进入下一步,否则重新进行迭代。本质上看,迭代次数要远高于其所得次数,其迭代次数的减少并不可靠。因此,以上研究虽然可以有效地得出较优的拆解序列,但是在其算法的迭代过程中或是未考虑优先约束,或是迭代速度过慢。
基于此,为提高拆卸序列规划的效率,在工程中更快、更精准地得出最优解,本文根据产品零件的装配约束关系,通过拆解优先图来表达拆解对象,并提出一种基于遗传-粒子群混合优化算法(GA-PSO);最后以液压泵作为算例,来验证算法的可行性及优越性。
1 产品拆卸优先图建模
1.1 拆卸优先图建立
本文所涉及的拆卸序列规划主要是完全拆卸,其目标函数一般为时间最短,所以选用较简单的拆卸优先图进行表达,若为选择性拆卸则不适用。
拆卸优先图可以简单有效地表达产品的拆卸优先约束关系[12],拆卸优先图如图1所示。

图1 拆卸优先图
图1中,A、B、C、D、E、F分别表示该产品的组成构件,有向箭头代表约束关系,表示各部件优先约束关系,如F→A表示在拆卸A之前,必须先拆卸F。
不同于之前研究的表达,本文所采用的拆解优先图使用分层表达,A为第0层,B、C为第一层,D为第二层,E为第三层,F为第四层。分层表达便于对序列进行“合规化处理”,“合规化处理”即为对随机序列进行处理使其满足优先约束。
1.2 模型的数学描述
DSP为离散组合优化问题,基于拆卸优先图模型,可将此问题描述为:
产品可拆卸单元为N个,每次仅能拆卸其中一个,所求序列应该满足拆卸优先关系,并且每个顶点都需遍历且只能遍历一次。
A-F按1-6进行排列,拆卸优先矩阵R如下式所示:
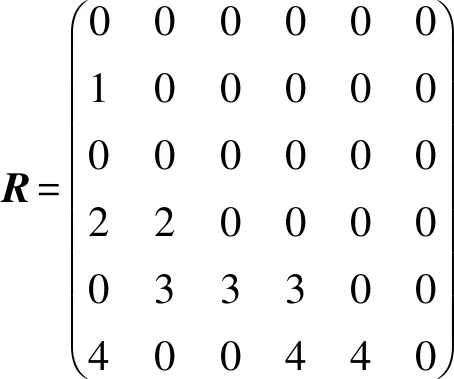
(1)
其中,Rrc—矩阵R的第r行第c列位置的数值,
Rrc=

4即为拆卸优先矩阵层数。
通过搜索优先矩阵可以将随机序列进行合规化处理,合规化处理流程图如图2所示。

图2 合规化处理流程图
M—拆卸优先矩阵层数
对于完全拆卸序列规划,其总拆卸操作时间一致,由于总时间=总拆卸操作时间+操作换向时间+变换工具时间,则可以将目标函数看作换向次数及工具变换次数的函数。该目标函数即可作为算法中的适应度函数。
(1)拆卸工具变换次数如下式所示:

(2)

(2)拆卸方向变换次数如下式所示:
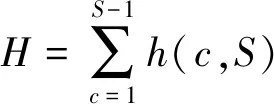
(3)

2 GA-PSO混合优化算法
2.1 算法原理及模型映射
2.1.1 算法1 (粒子群算法)
粒子群算法采用群体进化,通过适应度函数评价每个粒子的好坏,模拟鸟群飞行觅食行为,集体协作寻找最优解。将鸟群作为一个粒子群,每只鸟作为G维空间的一个粒子,其代表问题的一个可行解,具有位置和速度两个属性。
粒子位置坐标即为解向量,可通过适应度函数对其进行评价,各粒子可以通过自身所经历的位置、最佳位置和全局最佳位置提供的信息,在解空间内不断更新,寻找最优解[13]。个体最优解为粒子本身所经历的最佳位置,全局最优解为种群所经历的最佳位置。
传统的连续性寻优规则一般如下:
G维空间粒子i的信息可表示为:
位置信息如下:
xi=(xi1,xi2,…,xiG)
(4)
速度信息如下:
vi=(vi1,vi2,…,viG)
(5)
根据个体最优解和全局最优解进化,速度更新如下:
(6)
位置更新如:
(7)

2.1.2 算法2 (遗传算法)
解决拆卸序列规划问题可直接采用零件或者操作编号进行编码,通过选择算子对各染色体进行选择以得到父代染色体,再通过交叉、变异算子[14-16]。对种群染色体进行迭代寻找最优解。
传统的遗传算法中,选择算子一般选用轮盘赌选择法。具体方法为将每个粒子被选择的概率设定为该粒子的适应度所占种群总适应度的大小,若适应度越小越好,则通过各个粒子适应度与种群总适应度的差值之间的比值来确定。例如:3个粒子适应度为1、4、5,则总适应度为10,3个粒子被选择概率的比值为9 ∶6 ∶5,三者被选择的概率分别为0.45、0.3、0.25。
交叉算子一般是随机确定一个或几个交叉点的位置,然后将两个染色体的基因进行交换,从而选择两个新的个体。
变异算子一般是随机选择某染色体的某个位置,在其可变范围内进行按一定规则随机变化。
2.2 遗传-粒子群混合优化算法
粒子群算法多适用于连续组合优化问题[17],通过PSO求解DSP这种离散问题,需通过以下方法将其进行对应。
在产品模型基础上,产生多个粒子,每个粒子由1-N的自然数组成,即可构成一个粒子群:
(1)粒子的位置:对应拆卸序列;
(2)粒子的速度:前人将速度取值空间定为0,1来代表至下一代粒子元素是否发生变动。但是,通过此方式进行粒子的移动会产生不合规的粒子,需要再对粒子进行合规划处理。因此,本文取消粒子群中的速度概念;
(3)粒子的适应度:对应拆卸成本函数,其值越小,序列越佳。
遗传算法在求解DSP问题时同样需要进行改进,传统的交叉、变异算子可能导致从原本合规的父代染色体得到不合规的子代染色体。因此,要重新设计交叉及变异算子:
(1)交叉是GA更新和探索解空间的关键操作。传统的交叉算子可能会导致序列错误,比如FEDBAC与FECDBA在第3个点交叉则产生FECBAC与FEDDBA。
为保证基因的完整性,将使用优先选择交叉方式进行交叉[18],优先保存交叉算子如图3所示。

图3 优先保存交叉算子F1—父代1;F2—父代2;C1—子代掩码,C2—子代
步骤如下:①随机生成序列C1,该序列为1-2的随机排列,长度与染色体长度相同;②C1中第一个数字是1,则C2第一个基因从F1的第一个基因提取,并删除F1与F2中的该基因;③第二个数字是2,则C2从父代2的第一个染色体提取,并删除F1与F2的该基因;④重复以上步骤即可得出新染色体C2;
(2)变异算子。不同于传统变异算子,变异算子不能简单地选取任意两点进行置换,原因是交换后的染色体可能不能满足优先约束,合规化处理后可能与变异前相同,变异无效。对其进行改进,任取两点将两点间所有基因倒序排列,再经过合规化处理后变异有效的概率较高。
由于粒子群算法种群中一旦产生相对较优的粒子,则粒子都会朝着该粒子进化,若该粒子并非全局最优,且全局最优的方向与此粒子的方向相反,则粒子将无法找到全局最优解,使得其局部搜索能力较强。在对求解质量要求不高时,该算法可高效求得高质量的解,但并非最优解。因此,随着PSO算法的不断更新迭代,种群多样性必然减少,易陷入局部最优,从而得到局部最优解。
另外,拆卸序列规划问题是离散型数值寻优问题,且其序列顺序已被约束,这容易导致初始种群本身很可能已散落在局部最优解附近,以致无法寻找到全局最优解,从而得不出最优序列。遗传算法通过变异可提高其全局搜索性,将遗传算法与粒子群算法进行结合,可以增强粒子群算法的全局搜索能力。
称之为覆盖粒规则(xi)B→Dk的置信度,其中|·|指一个集合的基数。如果conf((xi)B→Dk)=1,则(xi)B→Dk称为一条确定性规则;否则称之为一条可能性规则。
因此,本研究提出了GA-PSO混合的优化算法。
遗传-粒子群混合优化算法流程图如图4所示。

图4 遗传-粒子群混合算法流程图
步骤一:设定算法基本参数,如种群数量,交叉、变异概率,粒子维度,约束矩阵,各零件拆卸的操作方向及工具信息,生成初始种群;
步骤二:对初始种群进行合规化处理;
步骤三:计算适应度,找出个体和全局最优;
步骤四:判断是否满足终止条件,条件一般设定为迭代次数或者达到所要求的适应度值,若达到终止条件则结束迭代,未达到则进行步骤五;
步骤五:各个粒子先后与个体最优解和全局最优解进行优先保存交叉操作,得到新的子代;
步骤七:对变异后的染色体再进行合规化处理,返回步骤三。
本文所提的混合算法主要是从用遗传算法来模拟粒子群算法的角度出发,重构遗传算法交叉及变异算子。从宏观上来看,其行为是粒子群算法;从微观来看,其行为是遗传算法,从而构成遗传-粒子群混合算法。
3 算例验证及分析
本文所用适用于产品拆卸序列规划的GA-PSO混合优化算法由MATLAB(R2018A)编程实现,电脑配置为:Inter(R)Core(TM)i7- 4710MQ CPU@2.5GHz,在Windows 8系统下运行,算法参数主要有粒子长度lenchrom,种群数量swarmsize,最大迭代次数maxgen和约束矩阵R。
以文献[19]中的液压泵为例,笔者对该产品进行分析。该液压泵模型包括20个最小拆卸单位。
液压泵拆卸优先图模型如图5所示。

图5 液压泵拆卸优先图
液压泵拆卸单元信息表如表1所示。

表1 液压泵拆卸单元信息表
算法训练过程如图6所示。

图6 算法训练过程
各算法结果对比如表2所示。

表2 各算法结果对比
由表2可知:5种算法均能得到近似最优解,但GA-PSO算法更为优异:蚁群算法、粒子群算法、遗传算法、改进人工蜂群算法所得最优解适应度分别为21、21、21、20。
与以上4种算法相比,一方面,GA-PSO算法所得最优解适应度为17,其解更优;另一方面,对比迭代次数与运行时间,GA-PSO的迭代次数远远小于以上几种算法,且运行时间与以上算法相比较短。
综上所述,本文提出的GA-PSO算法与其他算法相比更具优越性。
4 结束语
DSP问题作为维修前所必须解决的问题,组合优化极具挑战性。其一是由于其在进行排列中,存在着优先约束,使得模型的建立和算法的实现更加困难;其二是随着装配体可拆卸零件数量的增长,其排列组合将呈爆炸式增长,所以在建立模型和其求解算法时,要充分考虑这一现象。
本文通过拆卸优先图建立拆卸模型,并采用约束矩阵将模型表达为数学形式,不同于之前的研究,无需不断对约束矩阵进行迭代更新,将其作为约束运用于后续算法,可以方便地对序列进行合规调整;运用优先保存交叉方式和倒序式变异,对遗传算法进行了优化,再将遗传算法与粒子群算法相结合,改进了粒子群算法的易陷入局部最优的缺点。
最后,笔者以液压泵作为算例,验证算法的可行性及优越性,结果证明了其具有较好的全局搜索能力以及较快的收敛速度。
在今后的研究中,笔者将着手大型装备的多人协作拆卸序列规则;同时,此算法只适用于单人完全拆卸,笔者会在将来的研究中做进一步完善。

