摩擦副材质对超声波测量膜厚的影响

王 超，梁 鹏，2，3，郭 峰，王玉玲，姜芙林

（1.青岛理工大学机械与汽车工程学院，山东青岛 266520；2.中国科学院兰州化学物理研究所固体润滑国家重点实验室，兰州 730000；3.青岛理工大学工业流体节能与污染控制教育部重点实验室，山东青岛 266520）

0 引言

齿轮、轴承等机械元件依靠润滑膜来分离两接触面，正常工作时具有很长的使用寿命。然而，一旦润滑失效，两接触表面会发生接触和摩擦，随之而来的就是元件的磨损及胶合。润滑膜必须足够厚以此来隔离两表面，但是润滑膜太厚又会导致摩擦力增大，导致过量的泵力损失。因此，润滑膜厚度会影响液体润滑的质量，需要对膜厚进行测量，从而实时了解机械设备的润滑状态。

目前常用的润滑膜厚度监测方法主要有电学测量法、电磁测量法、光学测量法和超声波测量法。Lane等［1］通过电阻法对两啮合齿轮间的油膜厚度进行了测量。Lewicki［2］应用电容法测量了弹流润滑状态下的油膜厚度。Attia 等［3］通过两个E 形铁芯的磁力耦合，减小了磁涡流效应对膜厚测量精度的影响。王学锋等［4］对基于多光束干涉强度的弹流油膜厚度测量系统进行了相关研究。前3 种测量方法都需要对机械零件进行修改或者对应用条件有一定的要求，这限制了它们在工业上的应用，而作为非侵入性的超声波法通过对固液界面的反射信号进行频谱分析从而得到润滑膜厚度，更适合在工业中应用。

超声波技术可用于距离测量［5］，而近年来很多学者也将其用于液体膜厚度的测量。Dwyer-Joyce等［6-10］分析了润滑油膜不同厚度范围所适用的理论测量方法，并利用超声波反射系数法对轴承系统的润滑膜进行了测量。卢黎明［11］利用超声波脉冲反射法对滑动轴承的润滑油膜厚度进行了测量。超声波探头在使用前需要进行测量精度的标定，张强［12］利用不同厚度的塞尺进行探头使用前的标定，唐伟坤［13］利用在两玻璃盘间滴加润滑油的方式对0～30 μm范围的膜厚进行标定，杨晓［14］利用不同厚度的凹槽进行超声探头测量前的标定。

综上可知，目前超声波探头在使用前的标定方法不成熟，且标定装置存在标定厚度单一、小量程标定等问题。因此本文设计了一套机械可调式标定装置，用于超声波探头测量膜厚前的精度校准，且基于此装置研究了不同摩擦副材质对超声膜厚测量精度的影响。此外为分析实验结果，利用COMSOL Multiphysics多物理场仿真软件对实验模型进行了分析和验证。

1 超声共振法测量水膜厚度的理论模型

图1 为超声波在介质中的传播原理图，从超声波探头激发出的声波信号，通过界面0 后进入介质1 形成入射信号I1，当入射信号I1到达界面1 时，会产生透射信号T2和反射信号R1，而透射信号T2在介质2中向前传播到达界面2 时，又会产生透射信号T3和反射信号R2，此后透射信号T3在介质3 中继续传播。

图1 超声波传播原理图

为计算方便，设入射信号I1的振幅，则界面1 处的反射系数

式中：AR1是反射信号R1的振幅；z1是介质1 的特性阻抗值；z2是介质2（例如水）的特性阻抗值；z3是介质3的特性阻抗值；g=ejωh/c2；ω是入射信号I1的角频率；h为水膜的厚度；c2为超声波在水中的传播速度。

当发生共振时，根据波长公式λ=c2T（T 是超声波在水中的传播时间），可得其共振角频率为

式中：n为共振阶数（n=1，2，…）。若角频率ω 与水膜的共振角频率ωres相等时，则g2=1，整理式（1）可求得界面1 处的反射系数

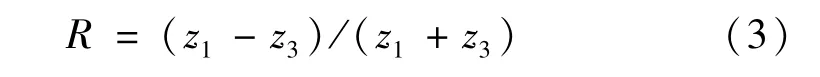
由式（3）可知，如果介质1 和介质3 的材质相同，即z1=z3，反射系数R=0。由此可知，在反射系数频谱图中，R=0 处所对应的频率即为水膜的共振频率fres，根据公式ωres=2π fres及式（2）可以得到水膜厚度

式中：fres为第n阶共振频率。

2 不同摩擦副材质间水膜厚度的测量

2.1 实验测量装置

如图2 所示为实验测量装置［15］，既可用于超声波探头测量精度的标定，又可以用于不同摩擦副间水膜厚度的测量。标定装置由右平移台带动右L 形板上下移动，从而调节右L 形板和左L 形板之间的距离，即对膜厚h进行调整。左L形板下底面与右L形板上顶面之间的实际膜厚通过MATLAB 软件对超声波探头采集的反射信号进行傅里叶变换得到，而理论膜厚则是通过高精度位移传感器测量右L 形板上表面粘接的钢柱位移得到，如图2（c）所示。装置中示波器的型号为Tektronix TBS 1102；超声波脉冲发射/接收仪的型号为Olympus 5073PR，超声波探头的型号为Olympus V111-RM；位移传感器的型号为ZA-210503-00-04-30-02，分辨率为1μm。图3 为3 种摩擦副材质图。

此空间小中见大，首先是还露斋与中间水景庭院的空间对比，与狭小的建筑还露斋相比，水景庭院尺度适宜，空间宽阔；其次是中间庭院的水景与建筑的虚实相映，使得空间疏朗雅致；最后是整个隐谧空间植物相互掩映，削弱建筑的空间限制感［3］。

图2 测量实验方案

图3 3种摩擦副材质

2.2 实验步骤

利用超声波探头采集图1 所示介质1-介质2（空气）界面的反射信号，并继续采集介质1-介质2（水）界面的反射信号，利用MATLAB软件编写的快速傅里叶变换程序进行频谱分析，从而得到图4 所示的反射系数曲线，找到曲线中的极小值点（即对应fres值）并代入式（4）可得测量的膜厚值。

图4 共振模型的反射系数曲线

2.3 测量结果及分析

图5～7 为不同材质摩擦副间水膜厚度的测量结果。将图中相对误差低于5%的范围设置为高精度测量区域；将5%～10%范围内的区域设置为中等精度测量区域；将10%以上的范围设置为低精度测量区域。图5 为两个不锈钢板间水膜厚度的理论值与测量值的对比结果。整体来看，膜厚的测量值接近于理论值，绝对误差较小；在整个测量范围内，几乎都处于高精度测量区，仅有一个点（理论膜厚为60 μm）位于中等精度测量区，此处的相对误差（5.27%）最大；而当膜厚大于160 μm后，测量精度非常高，相对误差甚至低于1.5%。

图5 两块不锈钢板间水膜厚度的理论值与测量值的对比

图6 为两个铝板间水膜厚度的理论值与测量值的对比结果。整体上，膜厚测量值的相对误差较小，只有两个点的相对误差位于中等精度测量区，而其他测量点的相对误差都位于高精度测量区，测量值的最大相对误差为9.17%（理论膜厚为50 μm）；而130～300 μm范围内的膜厚测量精度要明显高于30～130 μm范围内膜厚测量精度。

图7 为两个PMMA 板间的膜厚测量结果。从图中可以看出：低、中等精度测量区域各有一个测量点，其中最大的相对误差为10.81%（理论膜厚为30 μm）；除了这两个点外其他值均处于高精度测量区域；整体来看，探头用于PMMA板之间膜厚的测量精度也是比较高，且测量膜厚在110～300 μm的精度要明显高于30～110 μm。

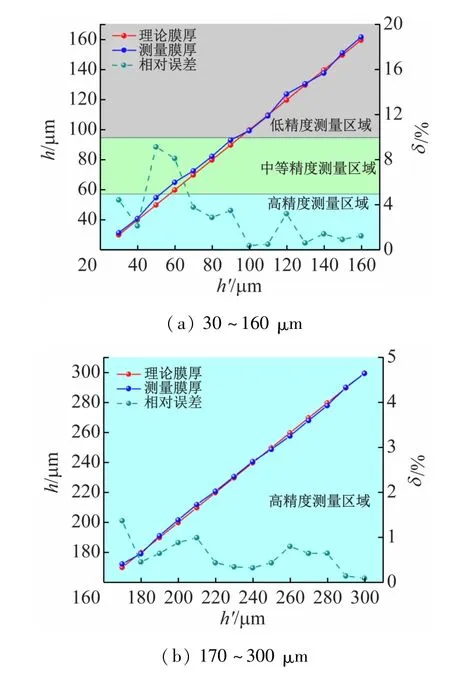
图6 两块铝板间水膜厚度的理论值与测量值的对比

图7 两块PMMA板间水膜厚度的理论值与测量值的对比

由图5～7 比较可知：①用于测量两个摩擦副板之间膜厚的探头测量精度较高，测量误差普遍低于5%，属于精度可靠的范围，且探头可以测量30 μm 以上的膜厚（更换高频率的探头可测量低于30 μm的膜厚）；②膜厚大小影响探头的测量精度，测量大膜厚时的精度要明显高于测量小膜厚时的精度；③板的材质会影响探头的测量精度，不锈钢板之间膜厚的最大测量误差为5.27%（低于铝板的9.17%，以及PMMA的10.81%），且测量误差只有一个点在中等精度测量区域，故探头测量不锈钢板之间膜厚的测量精度最高，其次是铝，最后是PMMA。

3 固液界面反射信号的声压仿真分析

声压是描述声波强弱的物理量。为分析上述实验中出现的现象（不锈钢板之间膜厚测量精度高于铝板、PMMA板间膜厚测量精度），研究摩擦副材质对膜厚超声测量结果的影响规律，本文利用COMSOL Multiphysics多物理场软件对探头接收到的反射信号（来自于固液界面）声压值进行了仿真。

3.1 不同阻抗边界声压传递的仿真模型

（1）模型建立。为研究图1 中固液界面1 处反射信号的声压，建立如图8 所示的声压传递二维仿真模型。

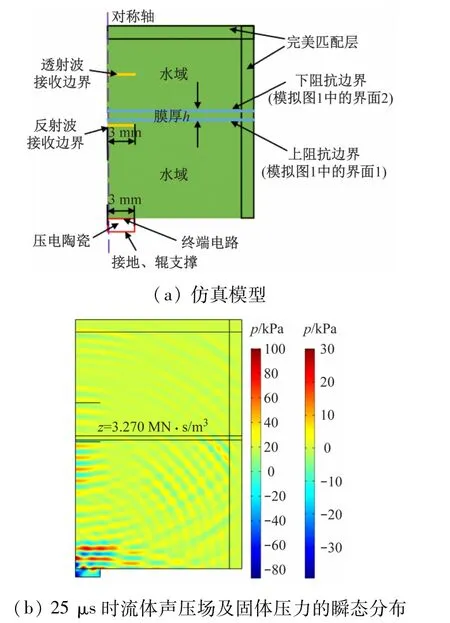
图8 声压传递二维仿真模型

超声波探头发射/接收脉冲主要是由内部的压电陶瓷实现，因此本模型用压电陶瓷代替超声波探头，压电陶瓷由中心频率为1 MHz，幅值为1 V 的简谐交变电压信号激励；上、下阻抗边界的阻抗值分别设置为不锈钢、铝和PMMA 的阻抗值，相关声学参数如表1所示。

表1 声学参数表

（2）边界条件设定。对压电陶瓷的下端设置接地和辊支撑，上端设置终端电路，实现超声脉冲的发射与接收；对上、下阻抗边界的阻抗值分别设置为3 种摩擦副材质的阻抗值进行计算；本次模型采用瞬态压力声学分析模块；模型通过设定圆柱形的完美匹配层（PML）来模拟无限远处的声场边界（见图8（a））。

（3）结果求解与分析。求解结果前，需要进行网格划分以及确定求解时间范围为（0，25 μs），图9 为模型的求解流程。对上、下阻抗边界和透射波、反射波接收边界的声压分布进行求解，结果如图10 所示。从结果可以看出：①由图10（a）可知，不同材质对上阻抗边界的入射声压分布无明显影响；②超声波为纵波传递方式，强度较高的声压分布于压电陶瓷片对应的宽度范围内（陶瓷片宽度为3 mm），即图10（a）和（b）图中红色虚线圈出的部分，且随横向距离的增加，不同材质对应的声压都趋近于0；③由图10（a）、（b）和（c）说明材质的阻抗值越大，透射声波的声压值越小，声波信号越弱；④通过图10（a）和（d）可以发现材质阻抗值越大，反射声波的声压分布曲线越高，反射信号的能量越大。因此，材质的阻抗值越大，产生的反射越多，透射越少。

图9 模型求解流程图

图10 不同边界处的声压分布曲线

3.2 不同摩擦副材质内部声压衰减的仿真模型

（1）模型建立。图8 所建模型是将图1 中的介质1 和介质3 等效成一个边界，忽略了声压在材质内部的衰减，这样可以保证相同的入射信号I1，从而单纯研究不同材质的阻抗值对声压传递的影响。但实际测量中，不同材质内部声压的衰减情况是不一样的，即图1中的入射信号I1会随着介质1 的材料不同而不同。因此，为定量分析声压在不同摩擦副材质内部的衰减情况，进一步解释实验测量的结果，建立如图11 所示的仿真模型。

（2）结果求解与分析。对3 种摩擦副材质内部的声压衰减情况进行求解，结果如图12 所示。声压分布从高到低依次为：不锈钢、铝和PMMA，说明声压在不锈钢内部的衰减最少，在PMMA 中衰减最多，且不锈钢在耦合界面处入射波声压的数量级远大于PMMA。

图11 材质内部的声压仿真模型

结合3.1 和3.2 部分的仿真分析可知，图1 中探头发射的超声波进入介质1，由于介质1本身的性质不同，其衰减程度也不同，不锈钢材质的衰减最小，PMMA衰减最大，故不锈钢与水分界面1 的入射信号I1最大，而PMMA 与水分界面的入射信号最小；当入射信号I1到达固液界面1 时，会发生反射和透射现象，且材质的阻抗值越大，产生的反射越多，透射越少，而三种材质中不锈钢的阻抗值最大，因此在固液界面1 的反射信号R1声压最高，所以探头接收到的反射信号能量最强、信息最完整，故不锈钢板之间的膜厚测量精度最高。

图12 耦合界面处入射波的声压分布曲线

4 结语

本文设计的超声波测量精度标定装置具有测量范围广、精度高、成本低等特点，基于此装置通过超声共振法实验测量了不同摩擦副材质间的水膜厚度。实验结果表明，膜厚的超声波测量值误差小，超声波探头的测量误差普遍低于5%；且摩擦副材质会影响超声探头的测量精度，两不锈钢板间的膜厚测量精度最高（最大误差5.27%），其次是铝（最大误差9.17%），PMMA 最低（最大误差10.81%）。通过COMSOL Multiphysics多物理场软件对实验模型的仿真表明，实验过程中两不锈钢板间膜厚的超声测量精度高是因为探头从界面1 处接收到的声波反射信号能量最强、信息最完整所致。