基于最优直方图的岩土参数概率模型的最大熵法研究
孔令奇
(成都工业学院材料与环境工程学院,四川 成都 610031)
在岩土工程的风险分析和可靠度分析中,岩土参数分布类型的不同将直接影响可靠度指标的计算结果,所以岩土参数概率特性的研究始终是一项基础性的重要工作[1-4]。研究人员做了大量的工作,从早期的基于参数估计的正态和对数正态分布的提出[5-7],到发现beta 分布拟合可以克服正态、对数正态分布无界分布的不足,将岩土参数基于参数估计的概率分布模型最终锁定在beta 分布[8]。但随着研究的深入,研究人员发现参数估计法拟合岩土参数概率分布时存在较大误差[9],故而提出非参数估计拟合方法,如正交多项式[10-11]、正态信息扩散[12-13]和最大熵法[14-15]等。
参考文献[14]指出最大熵法避免了一些非参数估计法过分依赖样本数据的缺点,最大熵法估计岩土参数概率分布精度和稳健性更高。参考文献[15]采用信息熵推断岩石力学参数概率分布模型,指出最大熵法根据样本信息和统计方法推断岩石力学参数的概率分布,具有更充分的数学和物理意义。
同时,通过对既有研究工作的总结分析发现,既有研究工作中一直忽略了一个基础性问题,目前各种岩土参数概率分布拟合方法,不论是采用参数估计还是非参数估计法,都将直方图作为评价概率分布拟合优劣的参考基准。目前频率直方图个数和区间的划分主要是研究人员凭主观决定。
为此,本文在既有研究基础上完成如下工作:采用最大熵法拟合岩土参数测试样本,根据岩土参数测试样本的特点,确定最大熵法最佳的矩的阶数;在最大熵法矩的阶数确定的情况下,研究直方图分组不同对岩土参数概率密度拟合曲线形状和误差的影响;借助判定系数,提出最优直方图分组方法;通过工程实际测试样本验证本文方法的有效性和合理性,完善最大熵法在岩土参数概率密度函数拟合上的应用。
1 最大熵法
1.1 基本原理
最大熵原理的概率分布估计是一个优化问题[16-19],如公式(1)。
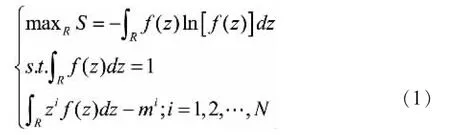
式中:S 为信息的均值,mi为第i 阶原点矩,N为原点矩的阶数。f(z)是随机变量z 的概率密度函数。若是用N+1 个参数形式表示的,则可用某种数值优化方法通过该模型求解出待定的参数。
通过式(1),改变f(z)可使熵达到最大值。S[f(z)]求最大熵分布的概率密度函数,可用经典微分方法求解式(1)。
设L 为拉格朗日函数,其拉格朗日乘子为λ0,λ1,…λN,于是:

令导数dL/df(z)等于零,则得:

归并积分号下的各项,得到:

由于积分式等于零,因此其中一种情况是被积函数等于零,由此可得:
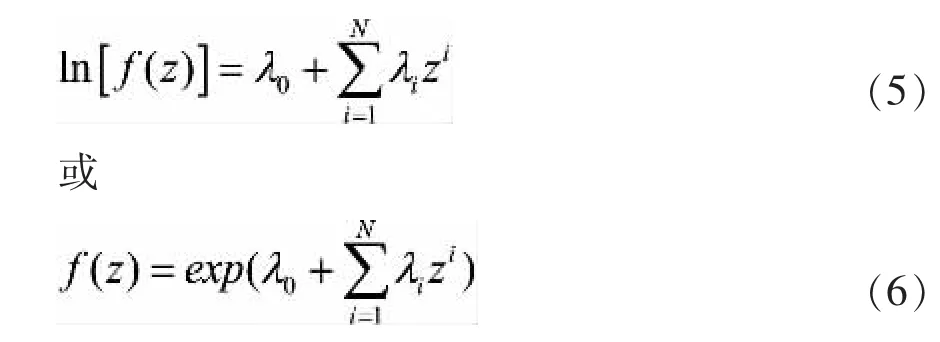
式(6)即为最大熵分布概率密度函数的解析表达式,也是式(1)的一个全城最优解。
1.2 乘子λi 求解
确定各个乘子λi(i=0,1,…,N),即可用最大熵分布表示变量z 的随机特性。

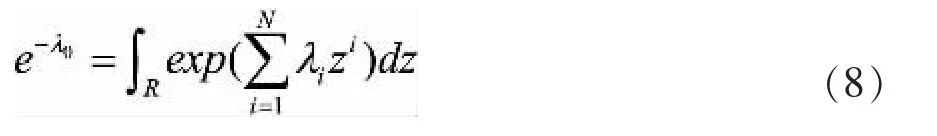
由此可得λ0的计算公式:

为求乘子λ1,λx,…,λN,可将式(8)对λi微分,得

或
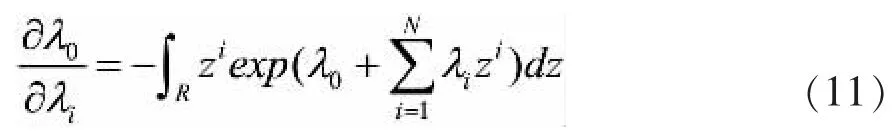
上式等号的右边就是第i 阶原点矩的负值,即

另外,若将式(9)对λi微分,又可得:

由式(12)和(13)可得:
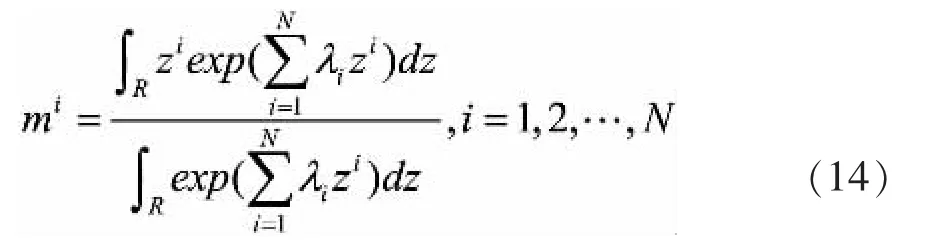
上式就是求λ1,λ2,…,λN的方程。对式(14)作如下处理:
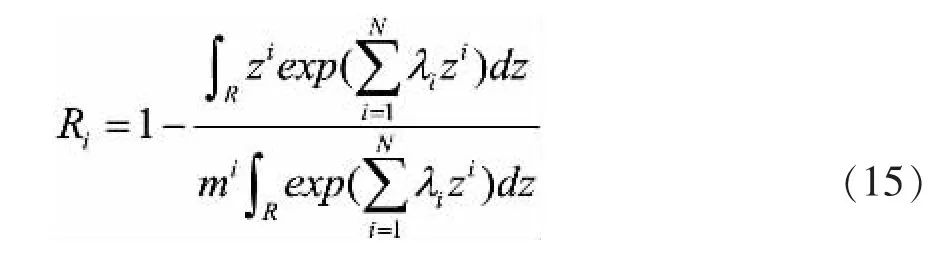
最后求

就可得到问题的解,其中Ri为残差。
求解式(16)时,需要输入一个初始点λi0(i=0,1,…,N),有一个好的初始点,对算法满意地收敛很重要。将式(1)的约束条件写成如下数值形式:

式中:aj是数值积分乘子。求解式(17)线性方程组可得N+1 个未知的f(zj),将它代入式(6),则有f(zy)=exp(λαλ1zj+…λNzjN);j=1,2,…,N+1 个方程,由此解得的λj(j=0,1,2,…,N)值即作为初值。
1.3 最大熵法最佳矩的阶数
为了避免出现计算时发生溢出的可能性,可将z 值域变换到[0,1]之间来计算,为此,后文对岩土参数测试样本进行了极差归一化处理[21],即:
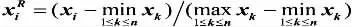
一般,当概率密度函数曲线形状比较复杂时,采用最大熵法拟合时矩的阶数要取大一点,但是必须注意,如果样本容量比较小,高阶矩的统计值会因误差较大而失去意义。
2 直方图分组不同对拟合效果的影响
2.1 既有直方图分组方法
在概率论与数理统计中,对于正态分布总体的随机变量,其直方图子区间的划分与样本数量有最佳关系,取分组数m=1.87(n-1)2/5。但大量的研究工作已表明,岩土参数测试样本离散性严重,呈偏态分布。所以,对于工程中非正态分布的随机变量总体,参考文献[20]指出,当样本个数大于50 时,可将直方图绘制时的分组数m 取为:

其中,n 为样本个数。
2.2 评价指标
K-S 检验法的检验量是整个取值范围内的最大偏差值,在一定的显著性水平下,可评估某一分布拟合的有效性,但不能提供某一分布拟合是否良好的绝对信息。为了评价拟合方法的优劣,引入一个无量纲的判定系数,它将拟合估计值与实际值对比分析,是直观评价拟合效果的指标[21]。判定系数定义如下
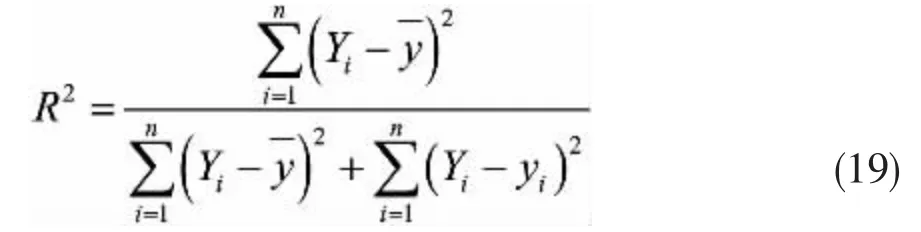
式中:yi为实测值,为实测值的均值,Yi为拟合估计值。由表达式可知,若实测值yi与拟合估计值Yi之间误差越小,则判定系数越接近1,拟合效果也就越好。
2.3 直方图不同分组对拟合曲线影响
下面以两组岩土参数测试样本为例,说明直方图分组不同对拟合曲线形状和误差的影响。选择参考文献[2]中提供的黏聚力和内摩擦角测试样本,共81 组,文中取直方图分组均为10,按经验公式(18)计算直方图分组为9。
采用最大熵法拟合两组岩土参数测试样本的概率分布,矩的阶数取为5~6,直方图分组不同时,拟合效果(判定系数)对比见表1,限于篇幅在此仅给出黏聚力样本不同直方图分组下拟合曲线对比如图1-2 所示。
对于两组岩土参数测试样本,由表1、图1-2 可见:对内摩擦角样本(矩的阶数为5~6)和黏聚力样本(矩的阶数为6),在直方图人为分组取10 和按经验公式取9 时,均未获得最佳的拟合效果,特别是内摩擦角测试样本在直方图人为分组取10 时的判定系数较直方图分组为8 的判定系数相差较大。

图1 矩的阶数为6 时黏聚力样本最大熵法拟合曲线对比
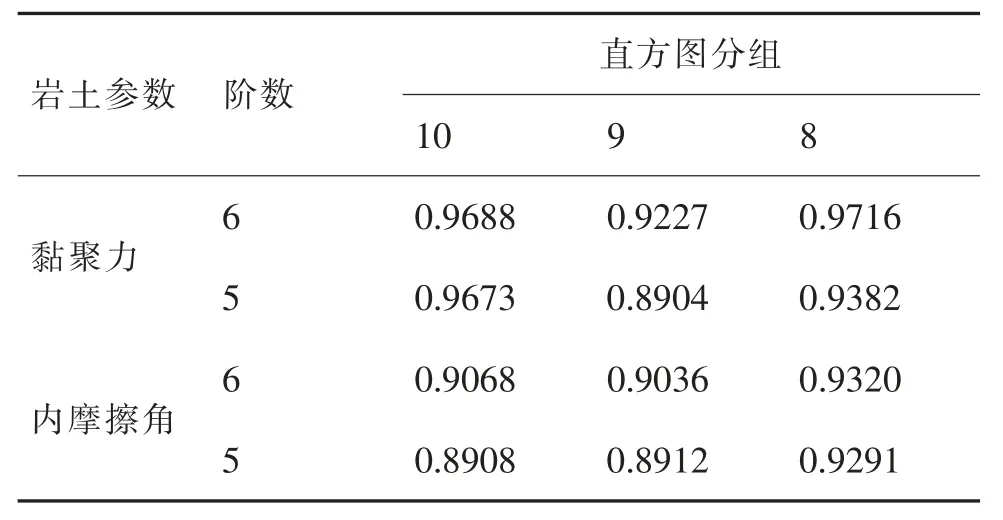
表1 拟合效果对比
综上所述,无论是通过拟合曲线的直观对比,还是通过检验值的定量检验,最大熵法拟合优劣取决于直方图的分组,如何确定岩土参数测试样本的最优直方图分组至关重要。
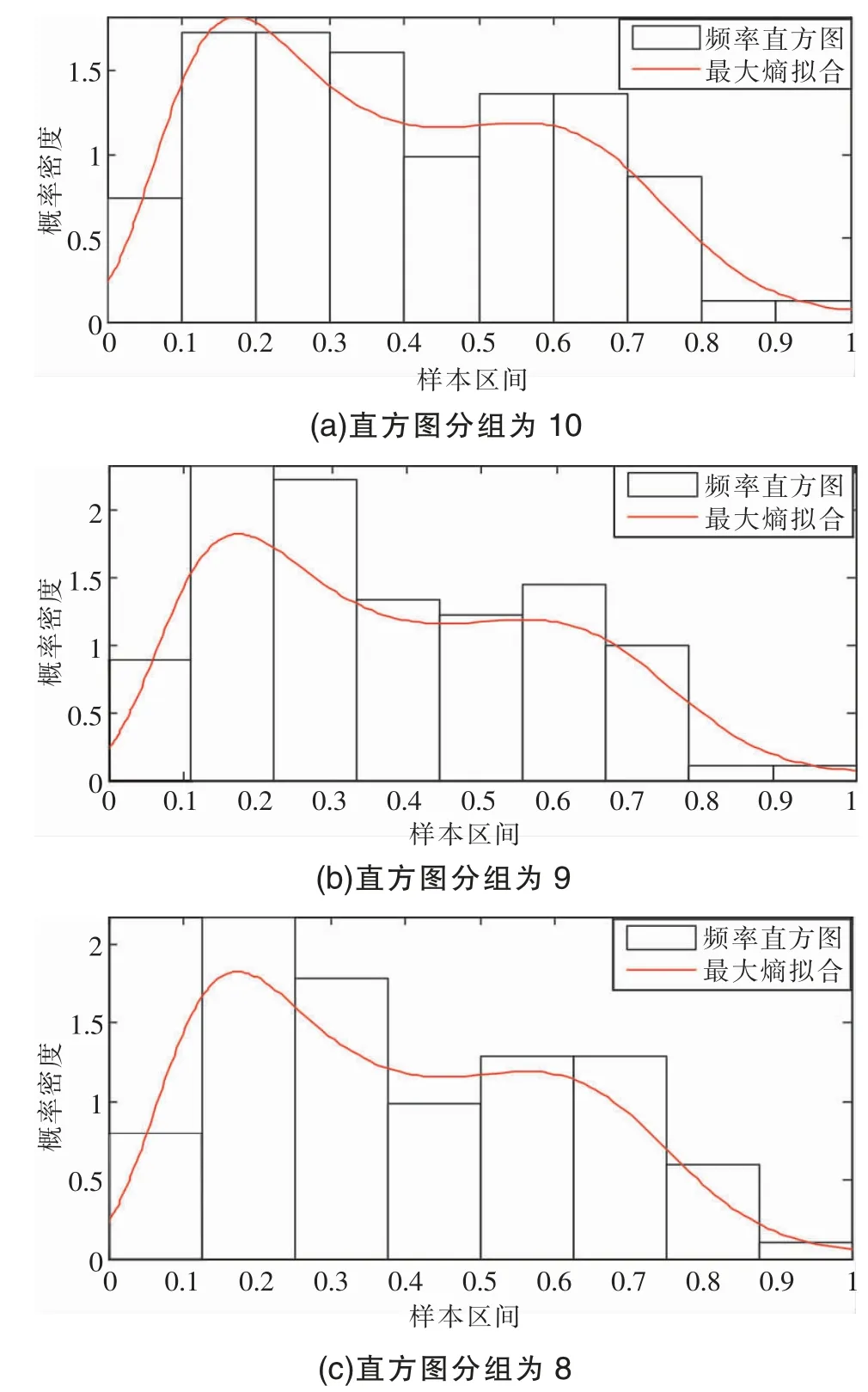
图2 矩的阶数为5 时黏聚力样本最大熵法拟合曲线对比
3 基于最优直方图的最大熵法拟合实例分析
通过上述分析可见,直方图分组不同,判定系数大小不同,在确定的最大熵法矩的阶数前提下,通过寻找最大的判定系数来确定最佳直方图分组是简单可行的方法。
仍以上述两组岩土参数测试样本为例,通过最优直方图分组数的确定方法,确定两组测试样本的最优直方图分组数。矩的阶数取5~6 时,在最佳直方图分组下的判定系数见表2。在最优直方图分组下,矩的阶数取为6 时,丙组岩土参数测试样本的拟合曲线如图3 所示。
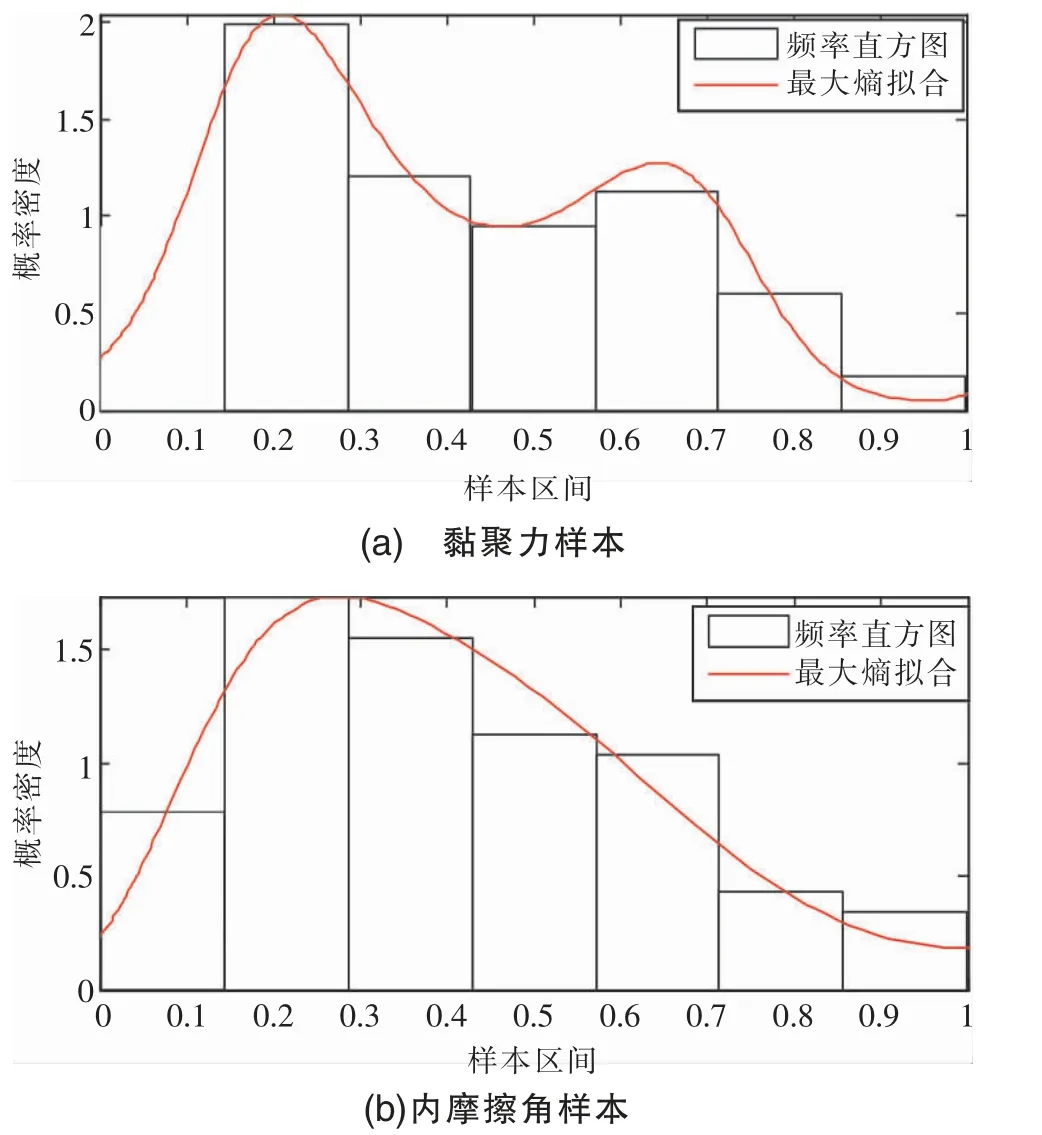
图3 最优直方图分组下的拟合曲线
由表1、表2、图1-3 可见,矩的阶数为5~6 时,最优直方图分组下的判定系数均大于表1 内的直方图分组下的判定系数,最优直方图分组下最大熵法拟合误差最小,拟合效果最佳。

表2 最优直方图分组下的拟合判定系数
为了说明确定最优直方图分组的必要性及论文方法的普适性,选取参考文献[13]提供的1 组摩擦因数小样本,样本个数为31,选取参考文献[11]提供的1 组液限小样本,样本个数为26。图4(a)为摩擦因数测试样本在矩的阶数取为5,直方图分组为7 时(文献中的直方图分组)的最大熵法拟合曲线,判定系数为0.8866。图4(b)为最优直方图分组为6时的最大熵法拟合曲线,判定系数为0.8975。图5(a)为液限测试样本在矩的阶数为5,直方图分组为6时的最大熵法拟合曲线,判定系数为0.9068,图5(b)为最优直方图分组为5 时的最大熵法拟合曲线,判定系数为0.9437。


图4 摩擦因数最大熵法拟合曲线
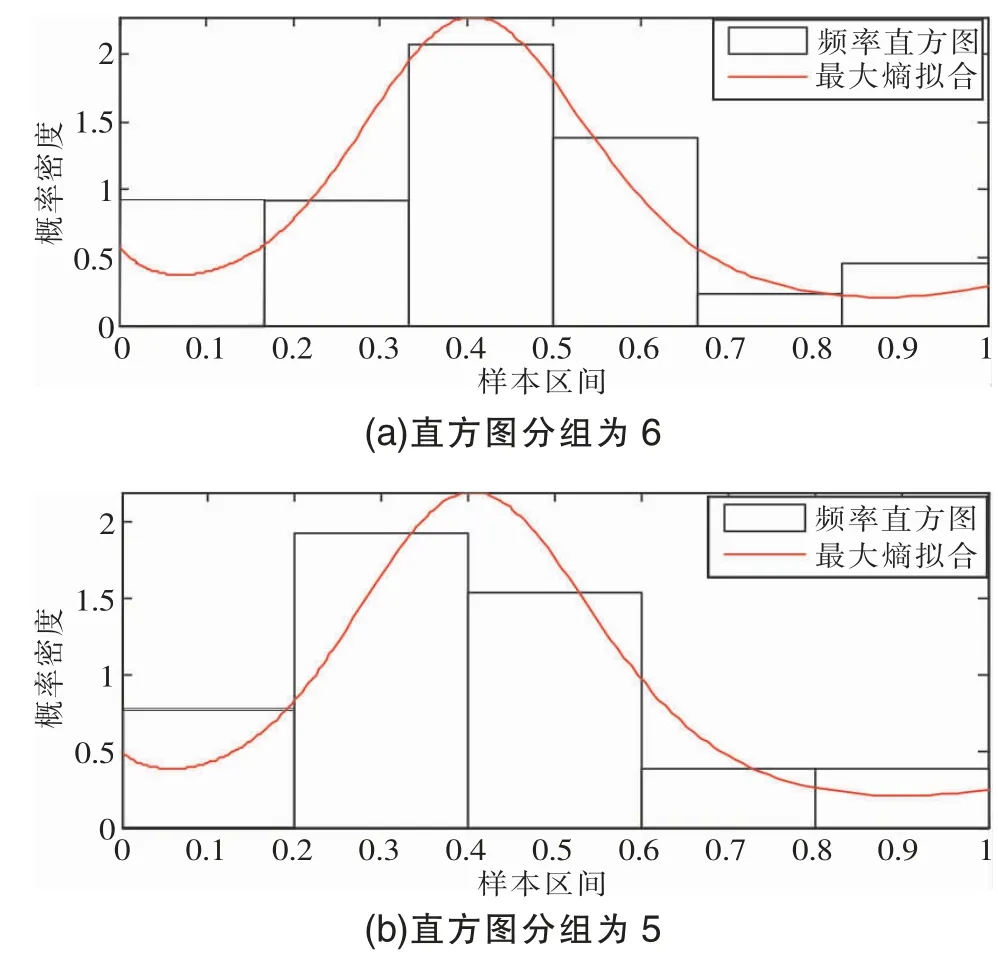
图5 液限最大熵法拟合曲线
针对两组大样本和两组小样本,无论是通过拟合曲线的直观对比,还是通过检验值的定量检验,均证明采用最优直方图分组后的最大熵法拟合精度均大于既有文献中直方图分组下的拟合精度。
5 结论
首次提出直方图分组的确定是最大熵法拟合岩土参数效果评价的前提和基础,在已有研究基础上,完善最大熵法对岩土参数概率密度函数拟合。既有的直方图确定方法人为因素较大,不能客观地反应样本概率分布。
实测样本的统计结果表明,采用最优直方图分组下最大熵法拟合岩土参数概率分布的判定系数最大,拟合精度最高,结果验证了基于最优直方图分组的最大熵拟合方法的有效性和适应性。

