深部巷道等强支护控制理论

左建平，文金浩，刘德军，吴丽丽，孙运江

1.中国矿业大学(北京)力学与建筑工程学院，北京 100083；2.煤炭资源与安全开采国家重点实验室，北京 100083

据统计，我国煤炭资源总量在2 000 m以浅约为5.9万亿t，其中埋深在1 000～2 000 m的资源量超过50%，且主要分布在中东部地区。依照目前的开采速度，预计未来20年内我国煤矿开采将进入1 000～1 500 m深度[1-5]。开采深度的加大伴随着地应力升高，导致深部巷道围岩在力学性质与浅部巷道围岩的不同。浅部地应力小，围岩大多处于弹性状态，而在深部，高地应力导致巷道开挖后围岩应力极易超过岩体屈服极限，使围岩出现大变形，进而导致巷道失稳[6-7]。有统计表明，由于受深部地应力环境、围岩体力学行为转变及工程条件的影响，超过90%的深部巷道围岩会出现大变形、松动坍塌及支护失效等问题[8]。而每年我国煤矿新掘进巷道长度可达12 000 km，巷道工程量巨大，因此对巷道支护理论与技术的探究与发展一直都是煤矿安全开采的核心内容之一[9]。

为保持巷道稳定，消除巷道片帮、冒顶、冲击地压、底鼓等安全隐患，从20世纪初开始，学者们相继提出了众多理论方法，为巷道支护设计的合理化作出了贡献。以普氏和太沙基为代表的塌落拱理论认为[10]：松散介质中硐室顶部会形成一个自然平衡拱，即“塌落拱”，普氏认为“塌落拱”的形状为抛物线状，而太沙基理解为矩形。该理论首次提出了巷道围岩具有自承载能力。20世纪60年代，Rabcewicz等在前人研究基础上提出了新奥地利隧道施工方法，简称新奥法(NATM)[11]。该理论选择性继承了传统理论中被动支护的理念，并提出主动支护的观点。20世纪70年代Salamon等人提出了能量支护理论[12]，认为巷道的掘进和支护存在能量转换，围岩与支护体在相互作用中释放能量，支护体吸收能量同时发生形变，围岩和支护体的调节实现二者的动态平衡。前苏联学者提出了应力控制理论，也称应力转移法、围岩弱化法[9]。该理论认为围岩破坏的主要原因是巷道开挖后，围岩受力状态发生了改变，可通过一定的技术手段(如钻孔卸压、开卸压槽、钻孔爆破、留设卸压煤柱等)改变围岩的应力分布，降低应力集中程度，使支承压力转向巷道围岩深处，从而提高巷道围岩的稳定性。郑雨天提出了联合支护理论[13]，认为巷道开挖后应进行柔性支护，允许巷道存在一定变形来释放部分变形压力，当围岩变形到相对稳定状态后再施加刚性支护，强调对围岩采用“先柔后刚、先让后抗、柔让适度、稳定支护”的支护原则。于学馥等提出了轴变论理论[14]，认为在两向不等压条件下圆形巷道围岩破坏的最终形态为椭圆形，并推导出巷道最佳轴变比的计算公式，对巷道的断面设计及支护设计具有指导意义。侯朝炯提出了围岩强度强化理论[15]，要点是锚杆支护能够改善锚固区岩体力学参数及性能，进而改善围岩的承载能力，同时锚杆与锚固区岩体形成承载结构，共同维护巷道的稳定。董方庭等提出了围岩松动圈理论[16]，认为巷道开挖后，围岩松动圈客观存在于围岩中，支护的主要载荷是松动圈形成过程中产生的变形与支护体的相互作用力，根据松动圈厚度，确定支护机理及相应的支护参数。何满潮等提出了关键部位耦合支护理论[17-18]，认为巷道总是从某一部位或几个部位最先开始破坏，并不断向其他部位发展最终导致巷道整体失稳的，强调只有当围岩与支护体在强度、刚度及结构上相互耦合时，巷道围岩控制才能取得较好的效果。方祖烈提出了主次承载区支护理论[19]，认为巷道开挖后围岩依次呈现张拉区与压缩区。压缩区对维护巷道稳定起关键性作用，具有较强的自承能力，即主承载区；张拉区形成于巷道浅部，只是起到了辅助作用，是支护控制的主要区域，即次承载区。康红普提出了关键承载圈理论[20]，指出任何巷道围岩内都有关键承载圈的存在，支护的目的是控制关键承载圈半径以内岩石的变形和稳定性，承载圈与巷道之间的距离决定了巷道维护的难易程度。左建平等针对矩形截面巷道提出了巷道等强梁支护理论[21]，强调根据顶板弯曲正应力的分布特征采用不同长度、直径的高强锚杆实现巷道各横截面上最大正应力相等，达到受力均匀的目的。王卫军等提出了内外承载结构理论[22]，外结构主要是注浆体、锚固体及支架等支护结构，内结构主要是以部分塑性硬化区和软化区煤岩体为主体组成的承载结构。外承载结构是主要承载结构，内承载结构是次要承载结构，对巷道围岩的稳定起关键作用。

在很多前辈支护思想的基础上，笔者团队基于深部巷道大变形或流变特性，提出采用巷道全空间协同支护来控制深部大变形巷道[23-24]。本文深入调查了巷道典型破坏模式，并对圆形与矩形巷道进行了力学分析，建立了巷道等强支护概念模型，进一步完善了巷道等强支护理论，为深部巷道围岩控制提供理论指导。

1 煤矿巷道典型破坏模式

巷道开挖前围岩处于三向应力的初始平衡状态，巷道开挖后打破了原有的围岩应力平衡，造成围岩应力重新分布，如图1所示。远离巷道的围岩受影响较小，处于三向受力的稳定状态，越靠近巷道受影响越大，围岩处于双向应力状态。因此在巷道径向会形成一定的应力梯度场，导致沿巷道径向的岩石破碎程度也不同，造成围岩发生梯度破坏[25]。

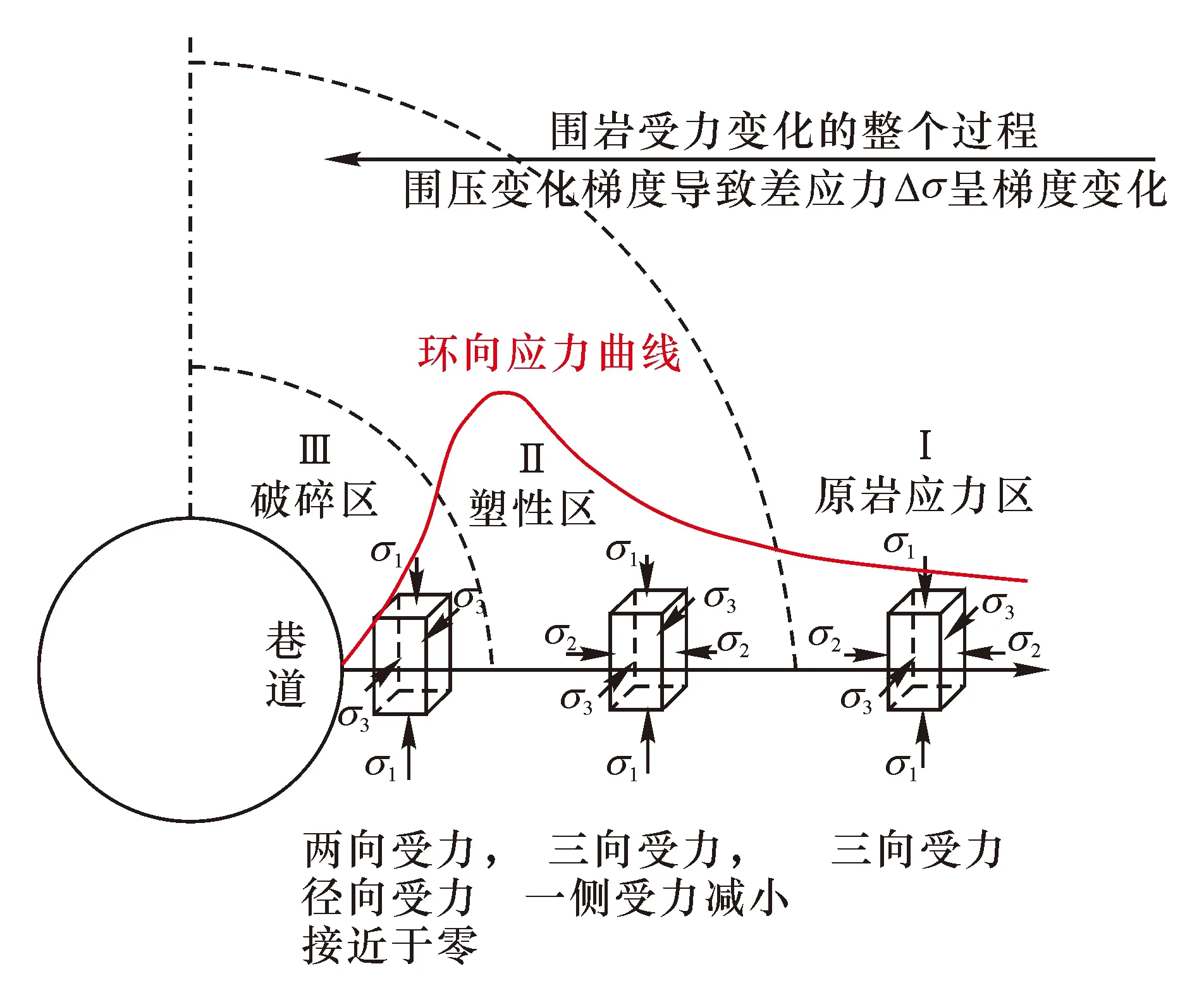
图1 围岩应力分布简化示意图[25]

围岩应力重分布导致应力梯度显现，当超过岩石强度后就会发生破坏。按照围岩破坏形态可划分为局部落石破坏、拉断破坏、剪切破坏、岩爆、潮解膨胀破坏、分区破裂化等[8，26-27]：

(1) 局部岩石破坏主要由施工与地质因素造成，破坏部位主要是顶板，其次是两帮，表现为岩块沿弱面拉断或滑移，如图2所示。

图2 局部岩石破坏模式

(2) 拉断破坏是由于围岩所受拉应力大于岩体抗拉强度后发生的破坏。按破坏区域分顶板拉断、两帮拉断、底板拉断三种形式。顶板拉断破坏易发生在顶板平缓且岩体抗拉强度较低的情况，表现为顶板弯曲下沉甚至垮落，如图3(a)(b)所示。两帮拉断破坏易发生在水平应力较大的情况，通常会出现两帮挤进甚至倾向巷道内的拉断破坏，如图3(c)(d)所示。在施工过程中，只注重巷道顶板与两帮围岩的加固，忽略了对底板变形的控制，使其成为围岩支护最薄弱的部位，当巷道变形时反向受力导致底板拉断破坏，巷道产生底鼓，如图3(e)(f)所示。

图3 拉断破坏模型

(3) 剪切破坏分顶板剪切、两帮剪切、底板剪切三种破坏形式。巷道顶板为节理较为发育的软弱岩体时，较高的切向应力通常会超过岩体的抗剪强度，从而沿着弱面产生剪切滑动，待节理贯通后形成塑性破坏区，如图4(a)所示；顶板为相对完整的岩体时，在高应力作用下顶板及角部岩体易发生剪切破坏，如图4(b)所示。两帮岩体无节理或节理较少时，在垂直应力与水平应力的共同作用下，促使两帮围岩出现某一角度的剪切破坏，破坏继续发展即会演变成两帮岩体向巷道内塌落，造成片帮，如图4(c)所示；帮部岩体强度较低时，在应力作用下两帮岩体会产生沿弱面的剪切破坏，导致两帮围岩挤进，断面变小影响巷道正常使用，如图4(d)所示。底板在受到较高水平应力下易发生剪切破坏，若底板为裂隙较多的软弱岩体，在应力作用下会发生剪切滑动，从而形成剪切破坏区，如图4(e)所示；若底板为相对完整的坚硬岩体，在水平应力的挤压下岩体会沿着弱面发生错动，导致底板向巷道内鼓出，如图4(f)所示。

图4 剪切破坏模式

(4) 岩爆是在一定条件下煤岩体中累积的弹性应变能突然猛烈释放时的脆性断裂，通常也称为冲击地压。岩爆易导致岩石崩落，并伴随巨大声响及气浪冲击，不仅影响矿山的正常运行及工人的人身安全，而且冲击波也会危及地面建筑物。

(5) 潮解膨胀破坏主要由巷道围岩遇水软化崩解或膨胀造成，通常发生在含有大量页岩、黏土岩、泥岩、硬石膏等岩石类型的巷道中。发生该破坏的围岩一般具有流变性、易风化潮解导致围岩强度降低。

(6) 分区破裂化现象是指在深部岩体中开挖硐室或者巷道时，在其两侧和工作面前的围岩中，会产生交替的破裂区与非破裂区，造成深部岩体呈现出明显的非线性力学行为，如图5所示。

图5 分区破裂化模式

2 典型形状巷道围岩应力场分布

为深入了解典型巷道破坏模式产生的机理，我们以圆形和矩形巷道为例，分析围岩受力状态并作如下假设：巷道水平布置，简化为平面应变问题；围岩为均质、连续、各向同性的弹塑性体；忽略围岩影响范围内的岩石自重。

2.1 圆形巷道围岩应力场分布

图6为圆形巷道力学模型简化图，由于结构对称、荷载不对称，因此该模型(模式Ⅰ)可视作两个简单计算模式的叠加。模式Ⅱ为均匀压应力场，模式Ⅲ为水平受拉垂直受压应力场。

由弹性力学知，圆形巷道在双向不等压应力场下围岩应力解[28-29]：

(1)

(2)

(3)

式中，σr、σθ、τrθ分别为径向应力、切向应力、切应力，MPa；λ为侧压系数；p0为垂直应力，MPa；R0为巷道半径，m；r为任一点到巷道中心的距离，m；θ为任一点到巷道中心的连线与水平x轴正向的夹角，(°)。

考虑不同的侧压系数，假设λ分别为0、0.5、1.0、1.5、2.0时，圆形巷道围岩应力状态取R0=1 m，p0=6 MPa，获得围岩中任一点与巷道中心距离为r的围岩应力分布，如图7所示。

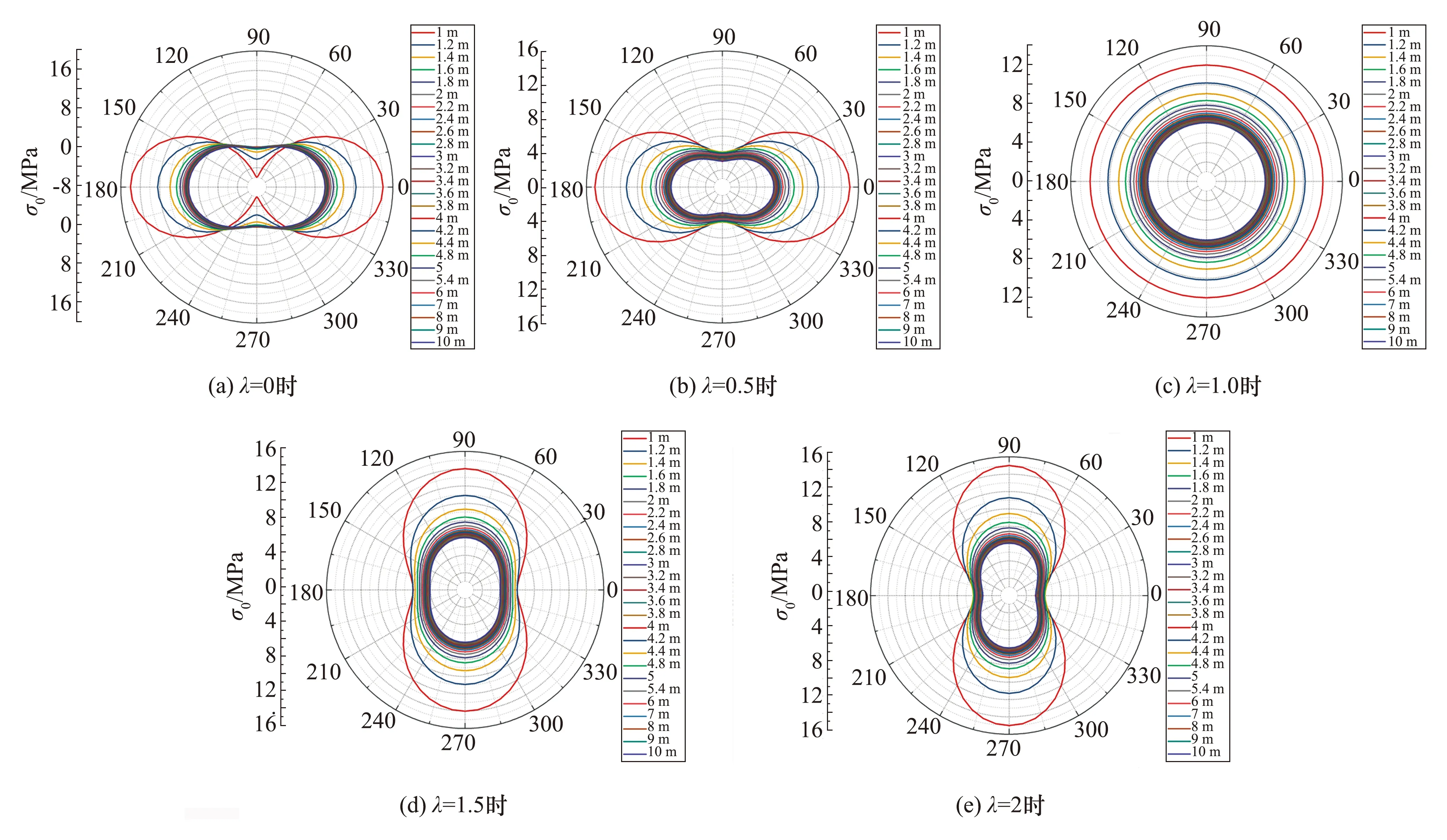
图7 不同侧压系数下圆形巷道围岩应力分布

由图7知，侧压系数λ对圆形巷道围岩应力分布影响明显。总体上，σθ从巷道壁向外围岩体逐渐减小，在巷道壁处σθ达到最大值。但λ不同时，围岩受力明显不同：当λ=1时，σr与σθ沿着巷道周边均匀分布，距巷道中心相同距离的各处受力相同；当λ<1时，σr在顶底板深部接近原岩应力，而σθ在两帮浅部出现应力集中，对帮部的破坏较严重；当λ>1时，σr在巷道两帮深部接近原岩应力，而σθ在巷道顶底板浅部出现应力集中，不利于顶底板的稳定。

2.2 矩形巷道围岩应力场分布

图8 Z平面矩形巷道到ζ平面单位圆的映射关系

复变理论中映射函数z=ω(ζ)将Z平面矩形巷道变换为ζ平面上的单位圆，进而求解围岩应力。围岩应力可通过解析函数φ(ζ)和ω(ζ)表示[30-31]：

(4)

对于矩形巷道，映射函数z=ω(ζ)由Schwarz-Christoffel积分获得，在保证一定精度的前提下简化为[31]

(5)

c1=cos 2kπ

因巷道无支护，矩形巷道浅处围岩只存在σθ，

σr与τrθ均为0，因此围岩应力由下式得出：

(6)

e=c1+(3c3-1)cos 2θ

g=c3(1+3c3)

h=(1+3c3)sin 2θ

矩形巷道c分别选取0.6、1.0、1.4、1.8，力学参数与圆形巷道相同，由式(6)计算λ分别为0、0.5、1.0、1.5、2.0时，围岩应力分布如图9所示。映射函数计算参数见表1。

表1 不同宽高比的保角变换参数

图9 不同宽高比及侧压系数条件下矩形巷道围岩应力分布

由图6可知：λ与c对矩形巷道围岩应力分布影响显著。σθ沿巷道边界分布不均匀，由两帮中部及顶底板中部向隅角处逐渐增大且呈对称分布，无论λ与c取何值，巷道隅角处均存在最大切向应力且为压应力。同时，当c<1时，随着λ的增大，巷道周边会出现拉应力；而当c>1时，λ的减小同样也会造成巷道周边出现拉应力。以上分析表明，巷道围岩不同位置可能会出现不同的破坏模式，巷道围岩处于受压或者受拉状态，取决于λ与c。

3 深部巷道等强支护控制理论概念模型

由巷道典型破坏模式及受力分析知，开挖后巷道断面不同位置应力梯度有明显差异，导致巷道发生不同破坏模式。当前煤矿巷道大多经验地使用一种或几种支护形式控制巷道围岩稳定，不仅造成支护的浪费也会导致受力较大处支护失效。

基于材料力学等强度梁概念[32]，我们提出了深部巷道等强支护控制理论概念模型。埋藏在一定深度的岩体，巷道开挖前处于同一层位的岩体可视作具有相同的初始受力平衡状态且不破坏，我们认为这是初始的等强状态。巷道开挖后围岩应力场被打破，在应力调整过程中会出现破碎区、塑性区和弹性区，因此需要通过支护、开槽卸压和注浆加固等手段来维护巷道的稳定性。若破碎区围岩和塑性区围岩的强度得到提升，理想情况下围岩各个位置支护后达到等强状态，并尽可能接近初始等强状态，让支护围岩呈现整体受力，以期实现不同位置围岩达到与地应力比相匹配的等效应力强度状态，这个时候围岩也能达到安全状态。由此，等强支护控制理论概念模型可以概述为：根据巷道围岩受力特征，通过开槽卸压、注浆加固、锚杆(索)主动支护、钢管混凝土被动支护等综合手段，有效调整巷道围岩的应力状态，使得周边各个位置围岩达到等强状态的支护方式。

针对此，在巷道支护中依据围岩破坏情况可通过围岩注浆加固使破裂岩体重新胶结成整体，提高围岩强度，改善围岩承载能力，如图10(a)所示；也可优先使用锚杆(索)进行巷道支护，将其与喷射混凝土、注浆加固技术相结合进行局部加固，如图10(b)所示；对于高应力巷道或者应力集中较大的巷道部位，采取应力控制措施(钻孔卸压、松动爆破、切缝卸压、开槽泄压等)，将巷道附近的高应力转移到围岩深处以确保巷道稳定，如图10(c)所示；对某些特殊地质条件(围岩松软、地压大、变形剧烈等)，钢管混凝土支架有其特有的优点；对于受拉应力的围岩，除上述支护手段外，可采用强梁支护方式、全空间协同控制技术、预应力锚杆(索)+桁架支护技术等措施加固[23-27]。

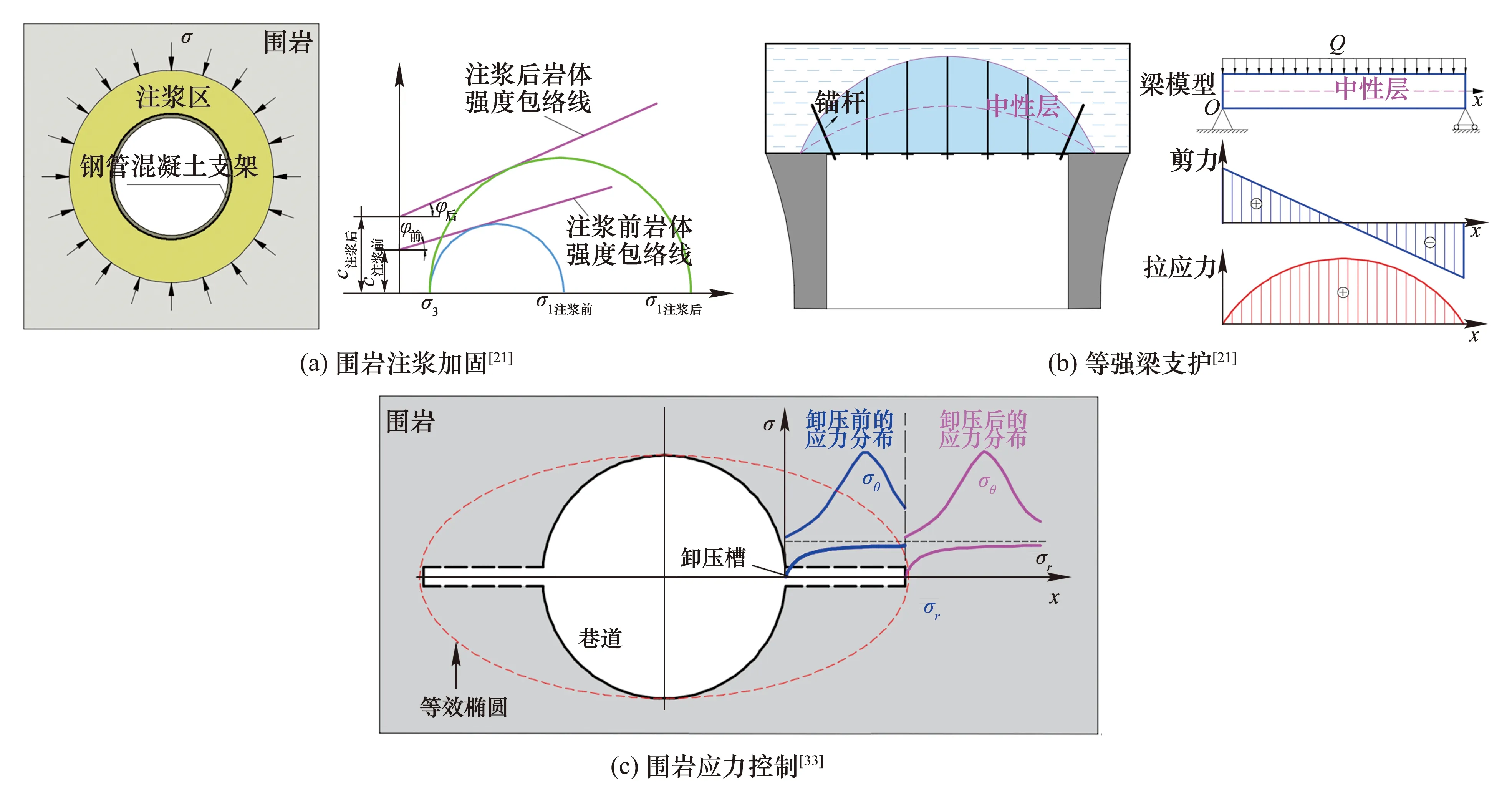
图10 巷道加固方式示意图

依据巷道破坏模式，当出现围岩应力集中、围岩破碎、拉应力区等情况时，合理采用应力控制、注浆加固、喷射混凝土、锚杆(索)、钢管混凝土支架及全空间协同支护等措施调整并控制围岩受力。在理想情况下，通过选取合理的控制措施让巷道周边围岩趋于均匀受压，以期实现不同位置围岩能达到安全且与地应力比相匹配的等强状态(图11)，此时围岩能够均匀协调变形，从而实现对巷道围岩的有效控制，保证巷道的正常安全使用。

图11 巷道等强支护控制理论概念模型示意图

4 深部巷道等强支护控制模型分析

为进一步描述等强支护控制理论模型，巷道开挖前及等强支护后围岩受力状态分析如图12所示。

平面应变条件下，极坐标表示的应力分量与主应力的关系[29]如下：

(7)

(8)

式中，σ1、σ3分别为最大主应力、最小主应力，MPa。

巷道开挖前，围岩的σ1、σ3数值差距不大，即巷道开挖前，莫尔圆1的主应力差(σ1-σ3)较小，远离支护前强度包络线L1，此时巷道围岩处于稳定状态。

图12 等强支护控制理论示意图

同时还应注意的是，当围岩抗拉强度小于围岩拉应力后，围岩发生拉破坏，此时支护的目的便是消除或减小拉应力，使之小于抗拉强度。巷道开挖引起的围岩应力重分布导致应力集中，应力超过围岩屈服强度会进入塑性状态，塑性区的范围影响巷道破坏的程度，因此合理有效的支护强度是维持巷道稳定的必要手段。

当采用M-C准则进行应力计算时，得到围岩起塑条件：

(9)

式中，C与φ为围岩的黏聚力与内摩擦角。

由巷道周边应力条件：σr=0，τrθ=0可以看出，在巷道周边岩体中主要存在σθ，当对巷道施加支护后可提高围岩的σr，改善围岩应力状态，从而提高围岩的承载能力。基于前人研究，将支护强度简化为pi，则巷道周边围岩径向应力变为σr+pi，切向应力为σθ-pi，将其代入式(9)得

(10)

由此得出巷道不同位置所需的支护强度pi：

(11)

式中，φ1为支护后围岩内摩擦角，(°)；C1为支护后围岩黏聚力，MPa。

φ1、C1可由现场试验确定，若未做现场试验，φ1仍可取φ，C1由下式得出[10]：

(12)

式中，σt为锚杆钢材的抗拉强度，MPa；S为锚杆杆体的横截面积，m2；e、t分别为锚杆间、排距，m。

式(11)中σθ由式(2)、式(6)求得，作用在巷道上的均布荷载p0可由下式计算[34-35]：

(13)

式中，En为巷道上方第n层岩层的弹性模量，MPa；hn为巷道上方第n层岩层的厚度，m；γn为巷道上方第n层岩层的容重，kN/m3。

当pn>pn+1时，则p0=pn，即应考虑该岩层上方n层对第1层的影响，第n+1层本身强度大、岩层厚，对第1层载荷不起作用。

由于巷道不同位置σθ不同，因此所施加的支护强度也会随着位置的变化而不同，使围岩在等强支护下能够处于整体受力均衡的稳定状态而不发生恶性破坏，保证支护体对围岩的有效支护。

5 深部巷道等强支护控制模拟分析

鉴于近年来高强度钢管混凝土支架支护技术框架已经初步形成，并已成功应用于多个深部矿井巷道及硐室的维护且取得了良好的支护效果，改变了深部巷道难以支护的窘境，如图13所示[36-39]。本文以钢管混凝土支架及锚杆(索)为支护主体进行围岩应力改善模拟。

图13 钢管混凝土支架现场应用实例

以某矿顶板巷道为背景，建立30 m×30 m×5 m的FLAC3D数值模型，模拟半径2 m的圆形巷道、3 m×3 m的矩形巷道围岩应力分布。模型采用M-C准则，力学参数见表2，边界条件为：四周与底部采用固定边界，上部为自由边界并施加垂直荷载10 MPa[39]，支护参数见表3和表4。

表2 煤岩力学参数表

由于侧压系数及巷道尺寸的影响，围岩应力在巷道周边分布极为不均，其数值模拟应力云图如图14所示。当前，煤矿巷道的支护大多采用主动或被动支护措施均匀地沿巷道断面施加相同规格的支护强度。由图7、图9及图14可知，不同侧压系数及巷道尺寸下，巷道断面不同位置处的围岩应力具有明显差异，而支护参数与支护强度选取的均衡化，不能满足受力较大区域的支护需要。在高地应力作用下，巷道周围受力较大处的围岩很容易出现岩层间滑移与错动，使之最先出现变形与破坏，并逐步扩展到整个巷道断面，造成巷道整体失稳。因此，对于巷道围岩中极易发生失稳破坏的部位应进行强化支护。

表3 锚杆、锚索参数

巷道开挖后，由于受力不同导致在巷道周围形成不同程度的应力集中，如图14所示。圆形巷道在两帮出现应力集中，顶板出现应力释放，矩形巷道4个隅角有应力集中的产生，顶底板及两帮存在应力释放，应力分布不均匀是造成巷道支护效果不佳的重要原因。针对本模型，圆形巷道在两帮采用卸压方式，将集中应力转移至围岩深处，同时巷道安设钢管混凝土支架，并在围岩中安装锚杆、锚索加强支护，通过合理采用围岩控制措施使得围岩应力分布趋向均匀，理想状态下的应力分布如图14(a)所示。对于矩形巷道，对围岩浅部进行注浆加固，隅角区域的力学参数折减一半用以模拟应力转移[27]，并在围岩深部安设锚杆、锚索提高支护强度，在围岩表面安装钢管混凝土支架控制浅部变形，以此实现围岩应力的改善，使之达到围岩呈近似均匀分布的理想状态，如图14(b)所示。

模拟发现，在合理运用了围岩控制措施后，围岩应力状态得以改善并且形成均匀分布或近似均匀分布的应力环，模拟验证了等强支护的可行性，为后续的深入研究提供了基础。

6 结 论

(1) 调研分析了煤矿巷道典型破坏模式，发现煤矿巷道主要存在拉伸破坏及剪切破坏，具体包括局部落石破坏、巷道顶底板及两帮的拉断破坏、巷道顶底板及两帮的剪切破坏、岩爆、潮解膨胀破坏、分区破裂化等6类15种破坏模式。

(2) 理论分析了圆形巷道与矩形巷道的受力特征，侧压系数及巷道形状显著改变巷道围岩的应力状态及破坏模式。在巷道支护中需要依据围岩破坏情况有针对性地施加支护手段，控制并调整围岩受力使其能够趋于均匀受压的理想状态，从而实现对巷道围岩的有效控制。

(3) 基于钢管混凝土支护、预应力锚杆支护及力学中等强度梁概念，提出了巷道等强支护控制理论力学概念模型。根据巷道围岩受力特征，通过开槽卸压、注浆加固、锚杆(索)主动支护、钢管混凝土被动支护等综合手段，有效调整巷道围岩的应力状态，以期实现不同位置围岩能够达到安全且与地应力比相匹配的等强状态。

(4) 推导出计算不同埋深、不同断面形状巷道所需的等强支护强度公式。数值模拟分析了圆形与矩形巷道在采用等强支护前、后围岩应力变化，验证了等强支护后围岩应力转变的可行性，为巷道支护研究提供了理论依据。