二维Poisson方程的快速求解算法

李金秀，李瑞平，袁黎景

(兰州职业技术学院， 甘肃 兰州 730000)

一、引言

Poisson方程是一种椭圆型的偏微分方程，在物理和工程领域具有广泛的研究，例如用来描述温度在区域Ω的分布情况. 本文中,将探讨如下二维的Poisson方程[1]的快速算法:

其中Ω=(0,1)×(0,1)是一个矩形区域，f(x,y)为源项，u(x,y)为待求的解.

二、有限差分离散

由边界条件为已知的零边界条件，只用考虑内部的点，即，网格点(xi,yj) (1iN1,1jN2). 本文中,令N1=N2=N,则h1=h2=h,

令ui,j为精确解u(xi,yj)在网格点(xi,yj)处的近似解，利用五点中心差分格式，有如下的二阶精度的近似离散形式[2]:

进一步，可以得到一个线性系统:Au=h2f，其中A=B⊗I+I⊗B，

⊗表示的 Kronecker 乘积;

I是一个N×N维的单位矩阵;

u=[u1,1,u1,2,…,u1,N,u2,1,u2,2,…,uN,N]T;

f=[f1,1,f1,2,…,f1,N,f2,1,f2,2,…,fN,N]T;

由此,我们得到了二维Poisson方程离散的线性系统. 为了提高计算精确度，就需要剖分出更细密的离散网格. 更多的离散点，更大的线性系统，需要更大的存储和计算. 下面，基于线性系统中的矩阵结构和离散的正弦变换，将构造出一种无矩阵的快速算法，即计算过程中不产生矩阵运算，只有向量点积运算.

三、求解策略

矩阵B可以被对角化[3]，形式如下：

B=QΛQT，

高校国有资产的管理要始终以人为本，坚持以学校的长远发展和学生的成长为需要配置资源。主动树立“我要管”的思想意识，将单纯的对物的管理提到对人的管理上来。

其中Λ是一个对角矩阵，

离散的正弦变换的计算量只有O(NlogN)，一般情况的计算中，Qv的计算量为O(N2)，Q-1v的计算量为O(N3)，这说明离散的正弦变化可以用来快速求解Poisson方程

对于二维Poisson方程线性系统的系数矩阵A，有：

A-1v=(Q⊗Q(Λ⊗I+I⊗Λ)-1QT⊗QT)v

对于这一步，我们可以利用多重离散正弦变换来实现计算。

四、数值实验

下面通过数值实验来说明所提出的算法在求解大型问题时的优势，对比方法为Gauss消元法. 所有的数值实验在MATLAB 2018b中实现，计算机处理器为Intel(R) Core(TM) i5-3470，内存16GB. 实验结果在表格中呈现. 表中“CPU”表示的计算时间，“Err”表示计算结果的相对误差，即 Err=‖uexact-u‖2/‖uexact‖2， 其中uexact和u分别表示精确解和数值解，“Order”表示格式的收敛阶，Orderk=log(Errk-1/Errk)/log(2). 所有的计算时间CPU(s)，是在计算10次后取平均得到的. “-”表示内存溢出无法计算出来的值.

例1. 考虑满足如下条件的二维Poisson方程:

源项f=-(12x2-12x+2)y2(1-y)2-(12y2-12y+2)x2(1-x)2，

精确解uexact=x2(1-x)2y2(1-y)2. 实验结果如表1:

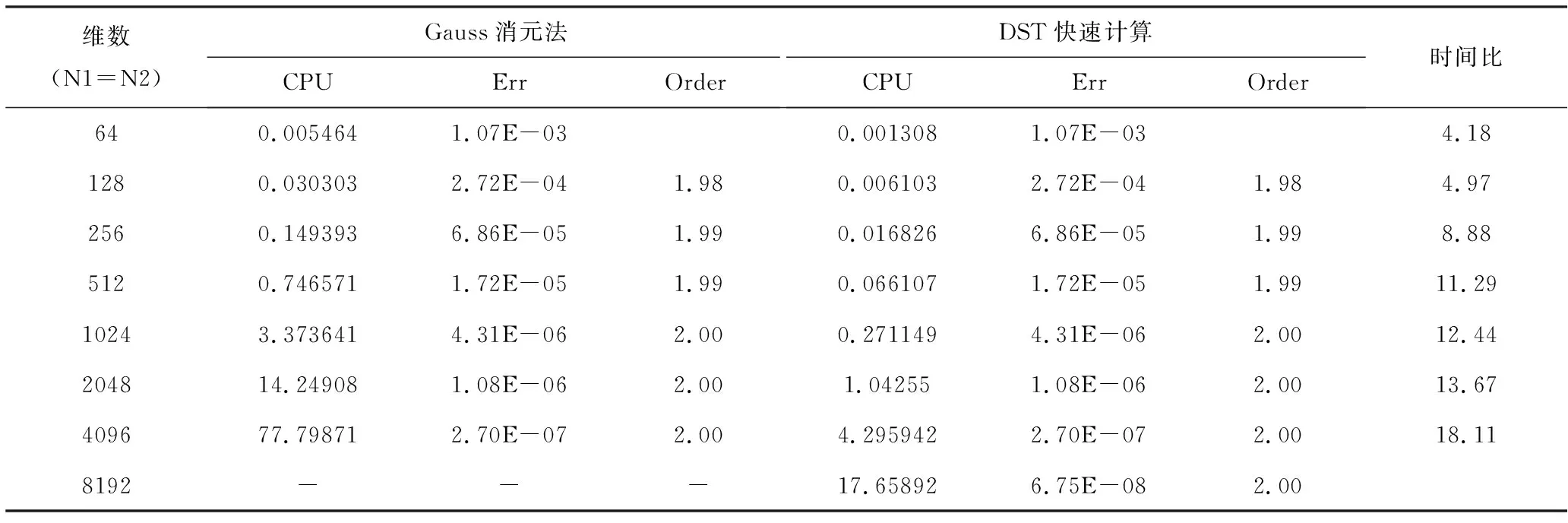
表1

从表中可以看出,两种方法的收敛相同,收敛阶接近或等于理论的二阶收敛. 从时间来看,笔者提出的DST快速算法,在时间方面有巨大的优势. 当矩阵越大时,时间的差距越大. 图1也显示了这一点.

图1 计算时间随网格点变化趋势图

此外，当离散点个数达到8192时，Gauss消元法由于内存不足而无法计算，但DST快速算法仍然可以进行计算. 这是由于DST快速算法在计算过程中并没有出现矩阵,是一种无矩阵的算法，这种算法的另一个优势就是节省内存，存储量从O(N2)降低到O(N).

五、结语

本文针对二维的Poisson方程提出了一种基于离散正弦变换的快速算法，这种算法降低了计算的存储需求和复杂度. 数值实验说明了笔者提出的算法是十分有效的. 可以进一步考虑将这种方法应用在更高维的问题和分数阶热传导方程中.