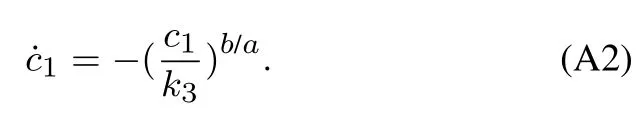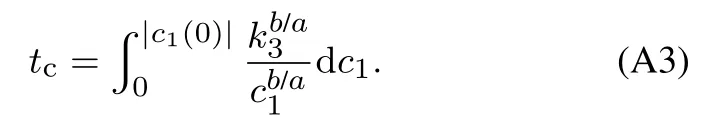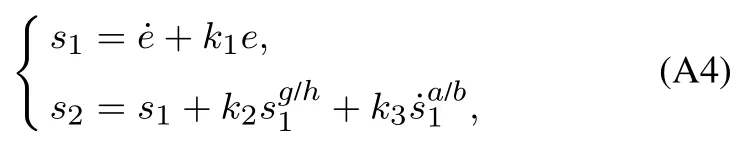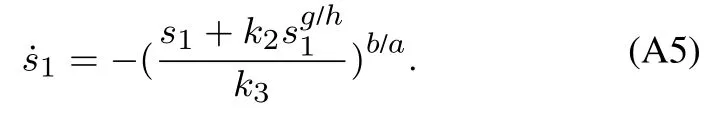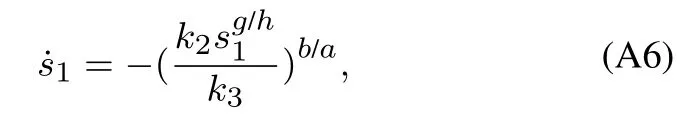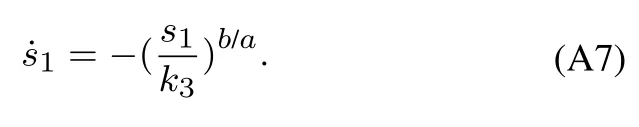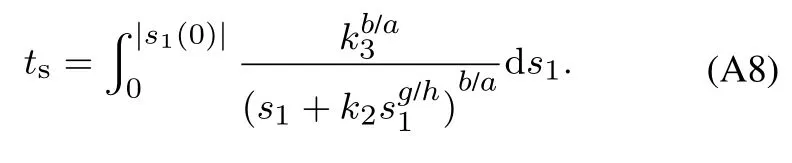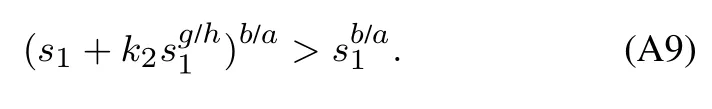动力定位船轨迹跟踪鲁棒自适应容错控制
王元慧,王海滨,张晓云
(1.哈尔滨工程大学自动化学院,黑龙江哈尔滨 150001;2.哈尔滨船舶锅炉涡轮机研究所,黑龙江哈尔滨 150078)
1 引言
随着全球经济的不断发展,陆地有限的资源已经不能够完全满足当前生活需求,因此海洋中储存的丰富能源的开发利用受到了科研人员的关注,其中动力定位船作为海洋开发的主要载体在其中扮演着重要的角色.面对着海洋系统复杂多变的环境和未知干扰情况下,如何能够安全且高效利用动力定位系统合理的获取海洋资源一直是我国兴海强国的战略目标,同时也是实践应用中的热点问题.对于动力定位船的研究不仅要考虑控制的鲁棒性(模型不确定和时变干扰)问题,而且要考虑控制过程中的实际约束(输入饱和约束)以及故障(推进器故障)问题,只有准确的解决了实际工程中未知干扰、系统参数漂移、推进器故障以及输入饱和问题才能够实现更好的控制效果且保证任务的顺利执行,因此具有广泛的实际应用前景和潜在的应用优势.
为了解决上述的问题,越来越多的相关研究如自适应控制[1]、反演控制[2]、模型预测控制[3]、动态面控制[4]、神经网络控制[5]、滑模控制[6]、容错控制[7]等不断的改善动力定位系统的控制性能,保障动力定位任务的高效执行.Fossen等[8]较早地针对动力定位船鲁棒控制问题提出了基于反演算法的全局指数稳定的非线性控制器设计,该方法很好地解决了动力定位船的鲁棒控制问题,但是该方法并没有考虑系统参数的不确定性和输入饱和等问题.在此基础上,文献[9]提出了基于反步法的模型预测控制,它很好的解决了动力定位系统的鲁棒控制,同时从节能角度考虑了系统的最优控制,使得该方法能够更好的为工程实践所服务.但是考虑到反演法的应用,通常在控制器的设计过程中会出现大量的求导计算,因而导致了“微分爆炸”问题,所以文献[10]介绍了动态面控制方法来解决这个问题,同时简化动力定位船的控制器的设计并保证控制器的控制效果.根据上述的研究可知,自适应控制以及滑模面控制等方法都拥有自己独特的优势,因此组合控制的方法逐渐成为了研究的关注点,将不同的控制方法进行相互组合,利用每个方法的优势,这样更有利于取得更好的控制效果.文献[11]提出了一种鲁棒自适应神经网络控制律,它采用了矢量反演控制理论,可以保证动力定位系统所有信号的最终一致有界.文献[12]同样设计了一种鲁棒自适应神经网络控制律,因此同文献[11]一样不仅补偿系统未知的干扰,还可以补偿系统模型的参数不确定性,与之不同的是能够简化控制器的计算负担,更好的实现控制器的设计效果.
为了更好地满足工程实践要求,文献[13]提出了一种适用于复杂干扰下的工程实践控制方法即滑模控制(sliding mode control,SMC).由于SMC具有响应速度快,对参数和干扰不敏感的优点,因此在工程实践中具有更好的鲁棒性.此后,SMC逐渐成为了重要的控制理论,SMC技术被引入到文献[14]中的浮式生产储油船的动力定位系统中,并且在时变扰动和模型不确定性方面具有良好的鲁棒性.为了提高滑模控制的性能,加快滑模控制的收敛速度并确保误差在有限的时间内收敛,在文献[15]和文献[16]中,动力定位系统控制器的设计中使用了终端滑模(terminal sliding mode,TSM)技术.此外,文献[17]探索了一种新颖的时变滑模(time varying sliding mode,TVSM)控制,以实现跟踪误差在有限时间内收敛为零且收敛时间的值可以预先设定.但是,TSM控制和TVSM控制方案可能无法保证无抖振现象下的稳定控制现象,因为抖振问题是由于SMC固有的不连续开关特性引起的.为了避免抖振对于控制性能的影响,出现了针对高阶滑模(high order sliding mode,HOSM)控制的研究[18–19],但在实际应用的过程中,收敛速度则成为了HOSM的重要缺陷.除此之外,同时考虑与动力定位船的鲁棒控制相关联的输入饱和[20]和推进器故障[21]等相关问题,亟待解决.因为动力定位船长期工作在恶劣的深海环境之中,加之部件老化等因素,推进器故障时有发生[22].一旦推进器发生故障,轻则造成任务失败,重则导致船舶失控进而造成重大经济损失甚至人员伤亡,因此故障容错控制(fault tolerant control,FTC)[23–24]的方法应运而生,包括主动容错和被动容错控制方法两种.文献[25]提出了一种具有执行器故障和传感器故障的动力定位船容错监督控制方法,与传统的故障检测和控制不同之处在于通过监督器将故障检测和容错控制器设计为一个单元并引入非线性估计误差和虚拟控制器的主动容错控制方法.文献[26]则是提出了一种将故障测量作为输入形式的鲁棒自适应容错控制器,而无需故障诊断过程的被动容错控制,进一步简化了控制器的设计同时提供了更良好的鲁棒性.在文献[26]的基础上,Yu等[27]又提出了一种基于神经网络改进的扩展状态观测器的容错控制方法,解决了模型不确定性以及未知干扰状态下的动力定位船容错控制研究.文献[28]利用对故障和干扰的部分信息,开发了使用积分滑模的有限时间无源容错控制方案,并实现了对无源故障的快速准确跟踪,同时提出了在线有限时间故障估计器.本文的目的就是设计一种有效的鲁棒控制方法来处理动力定位船综合约束问题,同时保障其故障发生时有足够的控制力来实现所需的控制目标.
基于上述问题的讨论和分析,本文的研究动机是通过综合SMC 技术以及推进器故障模型,针对动力定位船控制系统中的时变扰动,模型不确定性,推进器故障和输入约束情况,提出了一种新型的自适应神经网络二阶快速非奇异终端滑模(neural network and second-order fast nonsingular terminal sliding mode,NNSOFNTSM)容错控制方案.主要贡献如下:
1) 通过结合自适应高阶滑模控制和神经网络控制方法,提出了NNSOFNTSM控制方法并融入到鲁棒容错控制(FTC)算法之中,该算法在动力定位船控制系统存在未知干扰,模型不确定性,推进器故障以及输入约束前提下依然有效.这种方法首次将自适应NNSOFNTSMC与FTC相结合并应用于动力定位系统.
2) 在理论条件下,提出的自适应NNSOFNTSM容错控制方法不仅解决了系统的鲁棒控制问题,而且在推进器故障前提下巧妙地解决了控制系统的奇异问题并实现了快速收敛,同时将不连续的控制输入作用在滑模的二阶导数上,使得实际控制信号为不连续反馈控制的积分,因而削弱控制系统抖振现象.
3) 应用Lyapunov稳定性定理证明了系统所有闭环信号的有限时间稳定性.同时,证明了所提出方法可以在不依靠已知的模型参数和确切初始状态的前提下使用,因此,该方案能够更容易应用于工程实践.
本文的结构如下:第2部分是问题描述,简要介绍了有关动力定位船的运动学和动力学模型,推进器故障模型以及神经网络模型和相关引理等预备知识.在第3部分中,设计了自适应NNSOFNTSM控制器同时运用Lyapunov稳定性定理完成了系统闭环稳定性分析.第4部分通过数值仿真和对比实验证明了所提出的控制算法的有效性.最后,通过所有的分析和验证总结得到结论.
2 运动建模及预备知识
2.1 船舶运动模型
论文研究的主要内容是关于动力定位船执行轨迹跟踪任务时的控制问题.因此根据Fossen[29]所提出的动力定位船建模原理,建立简化的三自由度动力学和运动学模型如下所示:

其中:η[ηxηyψ]T表示的是动力定位船在大地坐标系下的位置信息,ηx代表的是沿x方向的纵荡位置,ηy代表的是沿y方向的横荡位置,代表的是绕z轴转动的艏摇角;ν[νuνvνr]T表示的是动力定位船在船体坐标系下的速度信息,νu代表的是纵荡速度,νv代表的是横荡速度,νr代表的是绕z轴转动的角速度;R(ψ)表示的是绕z轴的主旋转转换矩阵,其具体的形式如下所示:
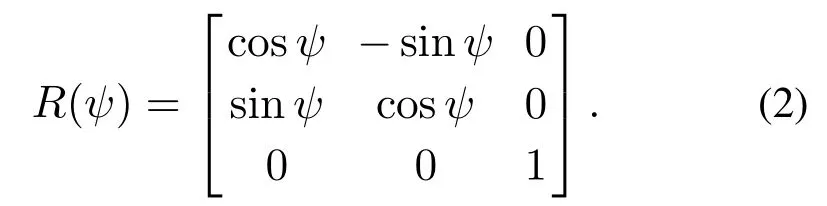
同时,转换矩阵R拥有如下的性质:RT(ψ)R−1(ψ).此外,矩阵M是系统的惯性矩阵,矩阵D是系统的阻尼系数矩阵,d(t)∈R3代表的是系统的时变干扰和外部作用力矢量,它将在下文给出具体的表达式定义.τ[τxτyτr]T表示的是控制力和力矩的大小,但是它受饱和函数的限制,如下所示:
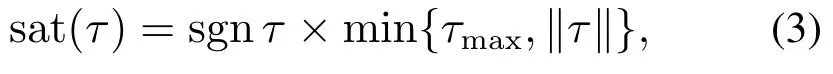
其中τmax表示的是控制输入向量的最大值.
为了方便后续滑模控制的滑模面的设计,给出动力定位船轨迹跟踪控制系统的跟踪误差的定义如下:

其中ηd表示期望的大地坐标系下的位置状态向量.
注1对于动力定位船而言,通常拥有比较小的横摇角ϕ和纵摇角θ,因此在系统控制中可以忽略不计.同时,动力定位船的工作场景都是处于低速行驶状态,于是在模型建立过程中科里奥利向心力也可以忽略.综上所述,如方程(1)所描述的系统表示将六自由度船舶运动学和动力学模型转换为三自由度运动学和动力学模型是合理的.
2.2 推进器故障模型
出于对冗余和鲁棒性的考虑,动力定位船的物理设施通常配备3个以上的推进器(包括了全回转推进器以及吊舱推进器等等).为了描述推进器的故障,系统(1)的控制输入τ进一步表示为
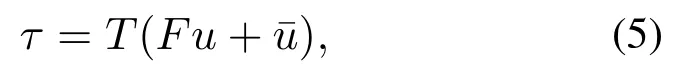
其中:T ∈R3×n(n≥3)表示的是推进器分布矩阵,其表征每个推进器对动力定位船的线速度和角速度的影响.Fdiag{λ1,λ2,……,λn}表示的是推进器故障(效率)矩阵,其中0 ≤λi≤1(i1,2,……,n)为故障(效率)因子.此外,u ∈Rn和∈Rn分别表示的是控制器设计的期望控制输入和偏差故障项,偏差故障项表示的是推进器实际信号与输入信号间存在恒定偏移或误差,通常由于推进器设备自身缺陷造成.根据动力定位船的推进器的故障类型以及式(5)的故障模型的表达式,本文假设不考虑推进器缺陷理想状态下(¯u ≡0)的故障模式为部分丧失有效性(0<λi <1)和完全失效(λi0)两种,λi1表示推进器正常工作.
注2论文研究的目标是三自由度的动力定位船轨迹跟踪控制任务,所以在考虑推进器故障情况时系统模型要满足式(6)的要求,这样才能够避免系统成为欠驱动系统,无法实现三自由度的控制效果,因此论文始终考虑动力定位船为全驱动系统的情况.

2.3 自适应神经网络模型
由于动力定位船控制系统存在着未知的模型参数,因此可以借助于函数逼近的思路来解决这个问题.神经网络(neural networks)算法凭借其优势可以逼近任何平滑函数,于是本文介绍了一种自适应神经网络逼近模型,该模型能够很好的估计连续函数并使其逼近真实值[30].

其中:fi(θ)表示的是连续的拟逼近的目标函数,θ[θ1θ2…… θq]T∈Ωθ ⊂Rq表示的是输入状态变量,Ωθ代表的是一个紧集;Wi ∈Rl表示的是权重向量;Pi(θ)[p1p2…… pl]T∈Rl和l分别表示的是神经网络模型中的激活函数和节点数目.
此外,根据原理可以得到整个神经网络算法的估计过程描述如下:
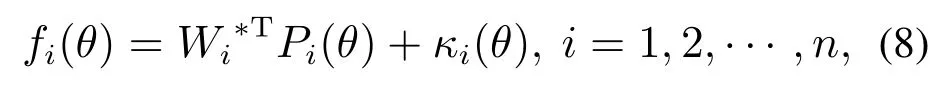
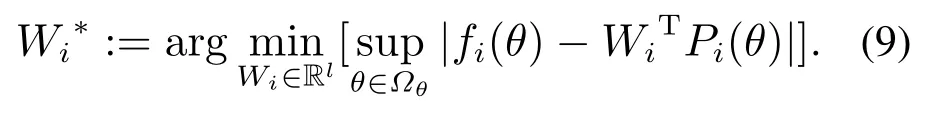
然后κi(θ)表示满足不等式|κi(θ)|≤κim(∀θ ∈Ωθ⊂Rq)的近似估计误差,而且κim表示的是未知的正常量.
本文根据最佳逼近性能,结构简单,训练速度快的特点,选择径向基函数(radial basis function,RBF)神经网络的估计模型.随后,激活函数选取了高斯函数的形式,其具体描述为
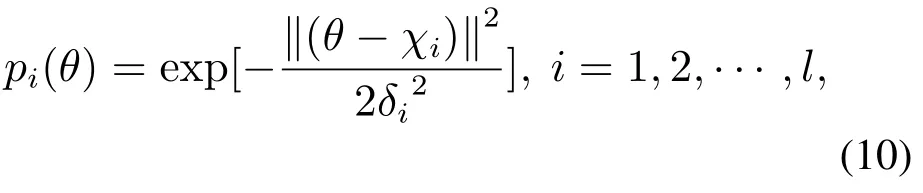
其中:χi[χi1χi2…… χiq]T表示的是第i个神经元的中心点;δi代表的是第i个神经元的宽度.
注3值得注意的是,根据文献[30]中的引理2,逼近误差κi(θ)是有界的,并且逼近误差与高斯函数的参数有关.因此,χi和δi的选择非常重要.
2.4 相关引理
引理1[31]假设矩阵T具有满秩的性质,然后,对于所考虑的所有故障情况,在满足式(6)成立的前提下,矩阵TFTT仍为正定.
引理2[32]如果存在着一个正定的连续函数V(x)在U ⊂Rn的实数域内对于∀x ∈U {0}总是满足不等式
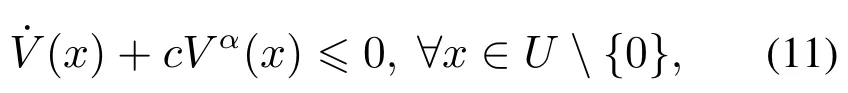
其中c和α表示的是正常量且0<α<1.
则存在一个开邻域U0⊂Rn,使得从U0开始的任意V(x)均可以在有限时间内达到V(x)0,收敛时间Tr满足Tr(x0)≤其中V(x0)是V(x)的初始值.
3 控制器设计
在本节中,将融合神经网络逼近技术以及自适应滑模控制方法,构造一种改进的自适应滑模容错控制器,其中选用的被动容错控制方法是基于鲁棒控制设计思想,将预先设想的故障视为系统不确定性构造故障模型,而后设计鲁棒控制器对其进行处理.闭环系统的架构如图1所示.
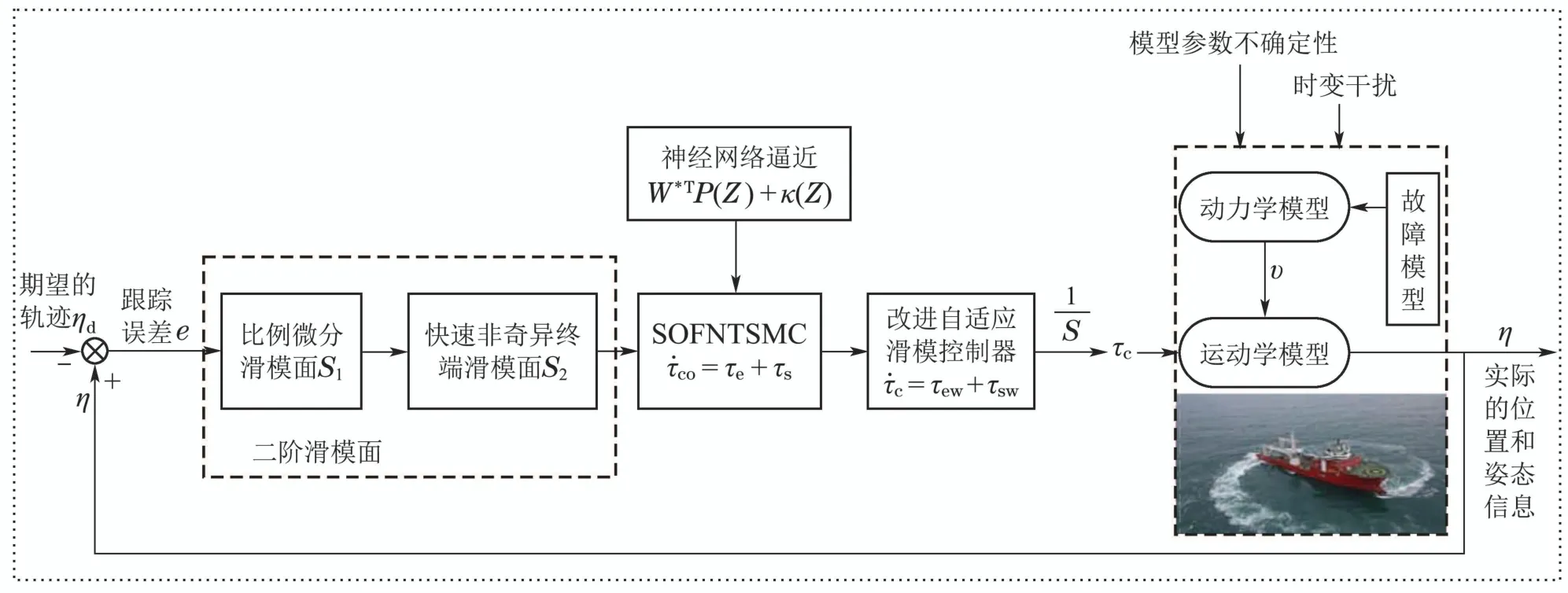
图1 闭环系统框图Fig.1 Block diagram of the closed-loop system
考虑系统(1)存在的模型参数不确定性啊,因此将系统(1)的第2个方程转化为如下表达式:
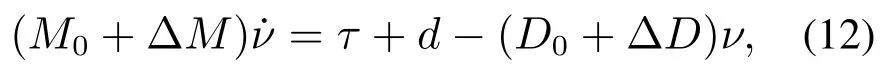
其中:M0和D0表示的是系统中的模型参数确定的部分;∆M和∆D表示的是模型参数不确定的部分.
根据式(1)(5)和式(12)可以得到如下的表达式:
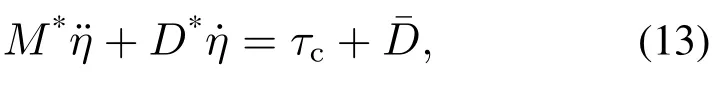
其中:
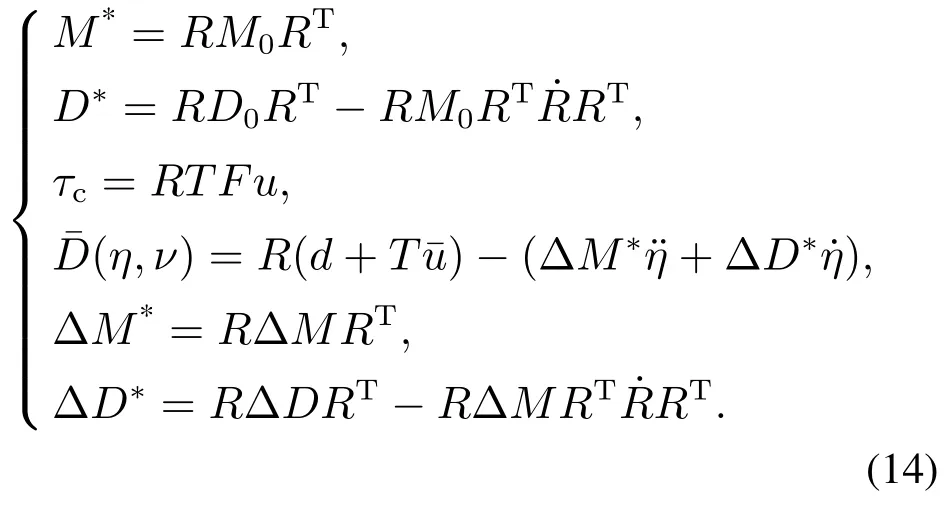
为了能够更方便地设计自适应二阶快速非奇异终端滑模控制器(second-order fast nonsingular terminal sliding mode control,SOFNTSMC),对动力定位船的状态变量做如下转换:

根据式(13)和式(15)可得如下的表达式:
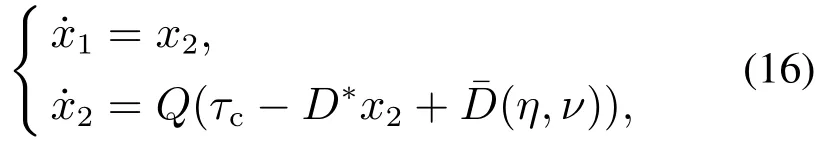
其中Q(M*)−1.
对式(16)的第2个方程求导可得
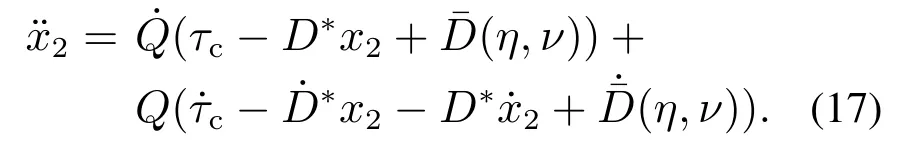
根据当前高阶滑模控制方法研究的启示,本文结合跟踪误差e设计了一种高阶滑模面,该滑模面由比例微分滑模面s1和快速非奇异终端滑模面s2组成,其具体的滑模面形式如下:
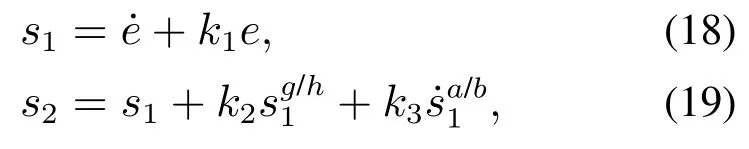
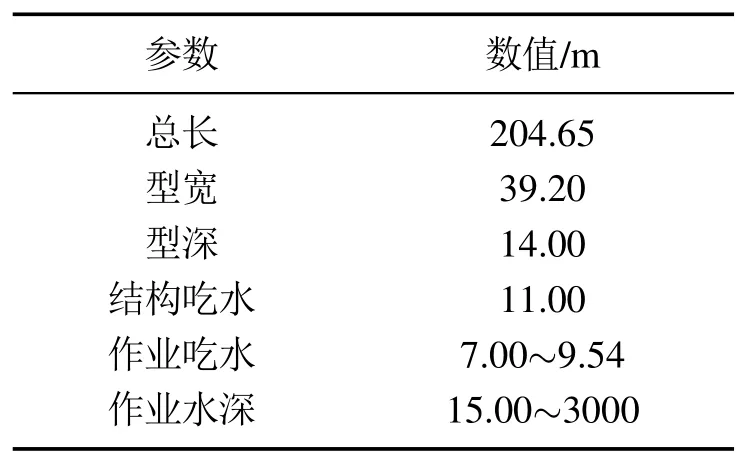
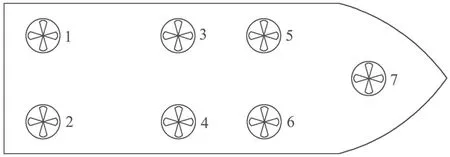
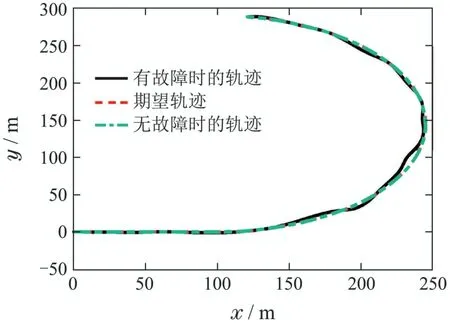
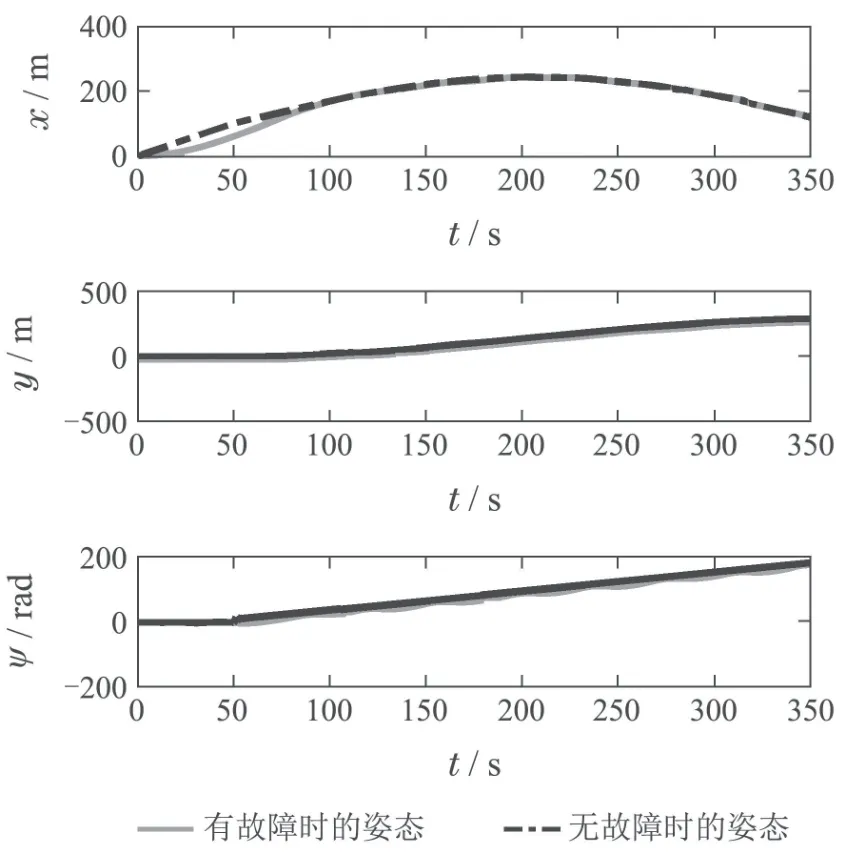
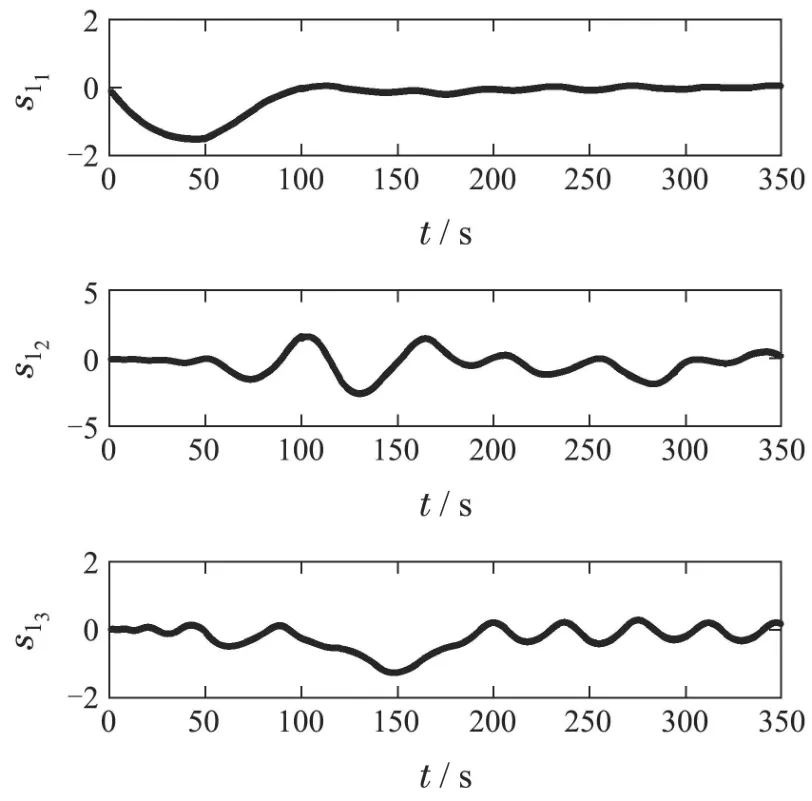
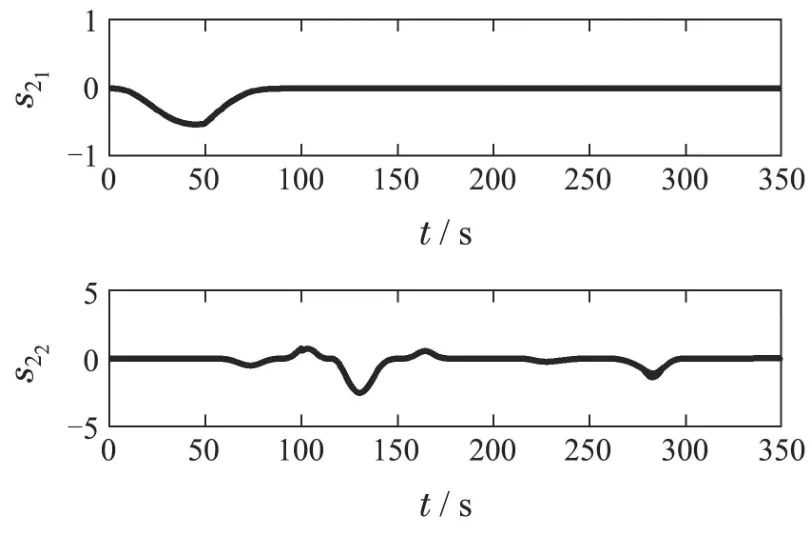
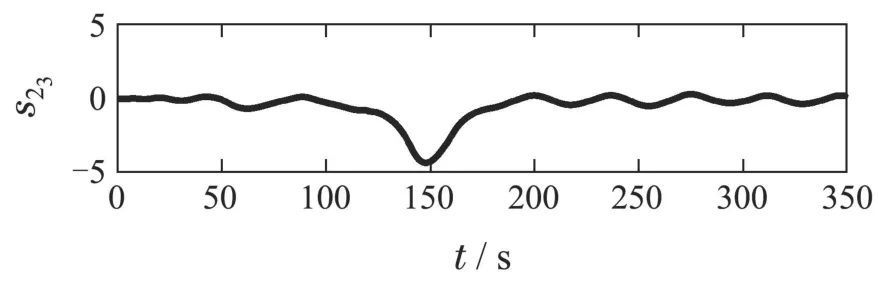
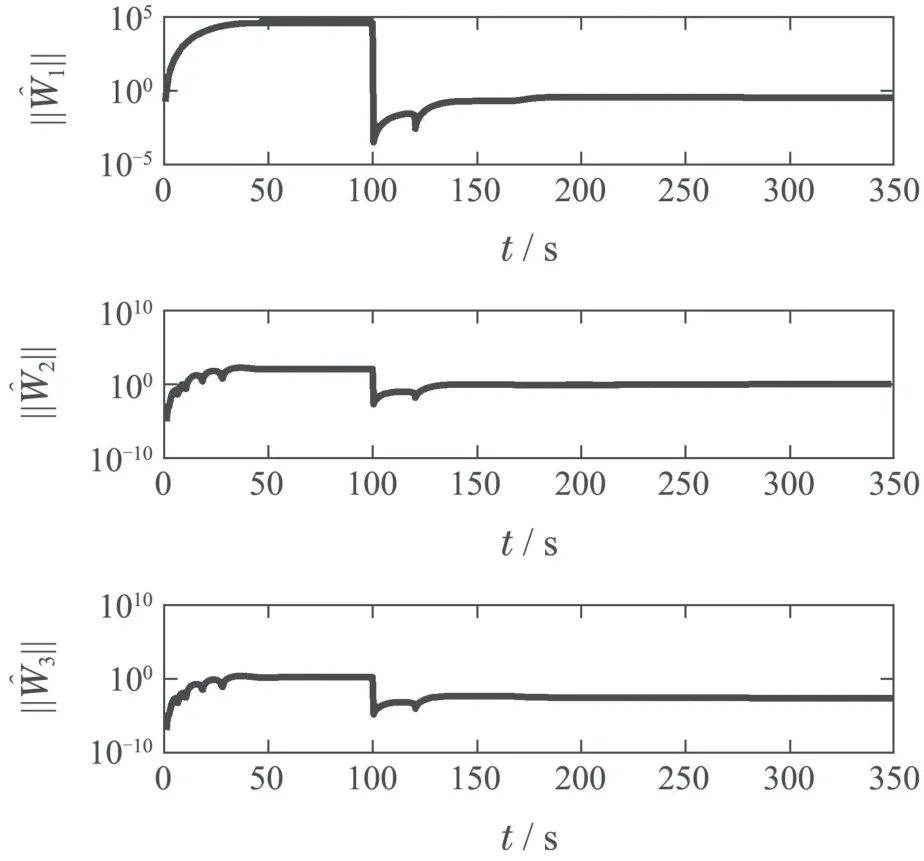
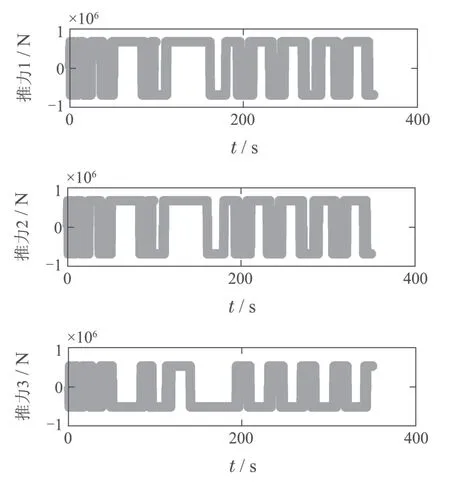
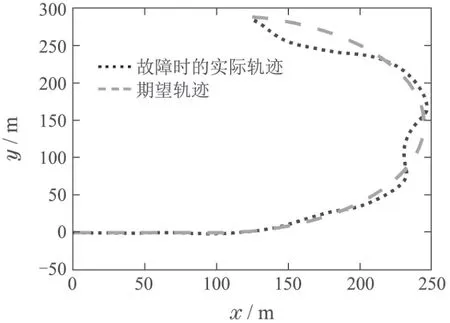
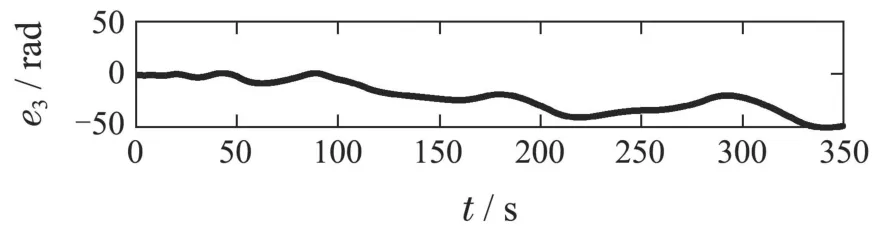
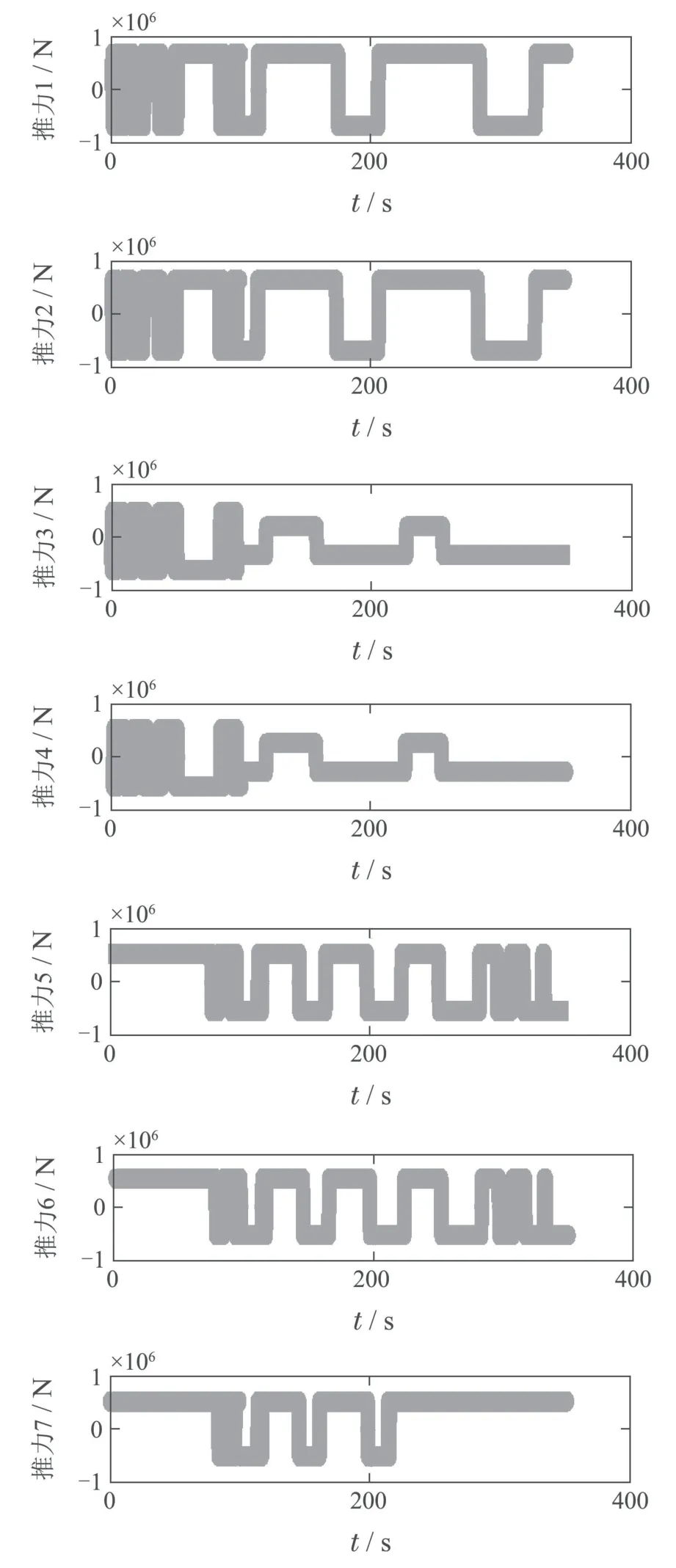
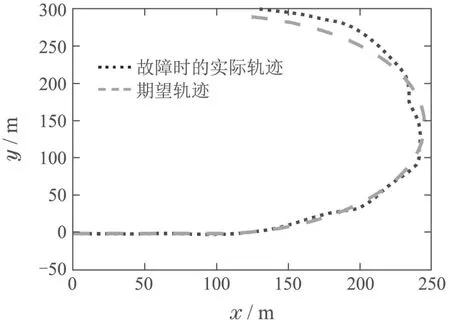
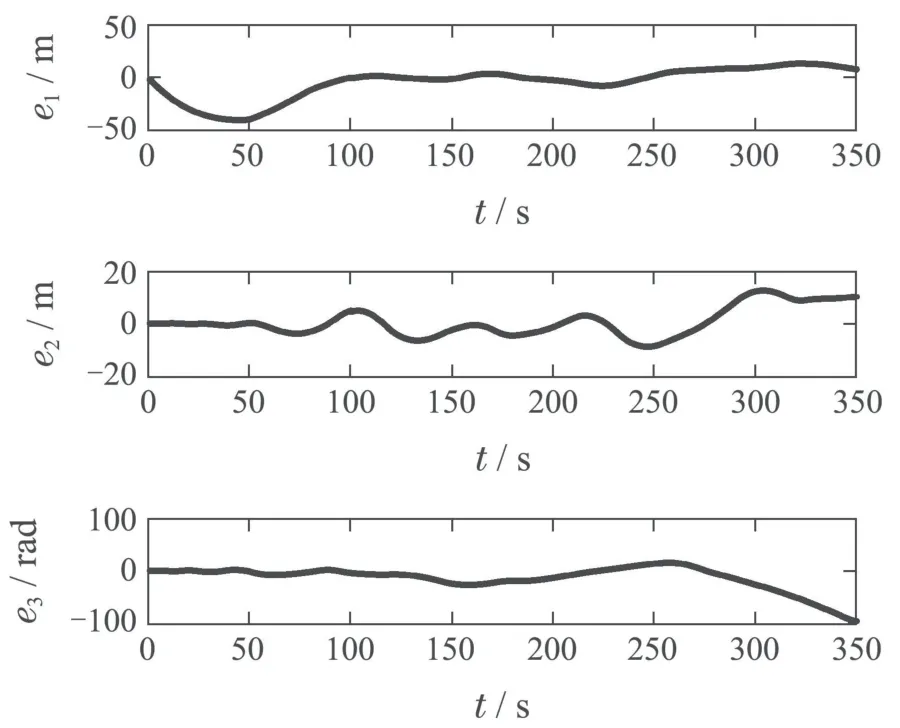
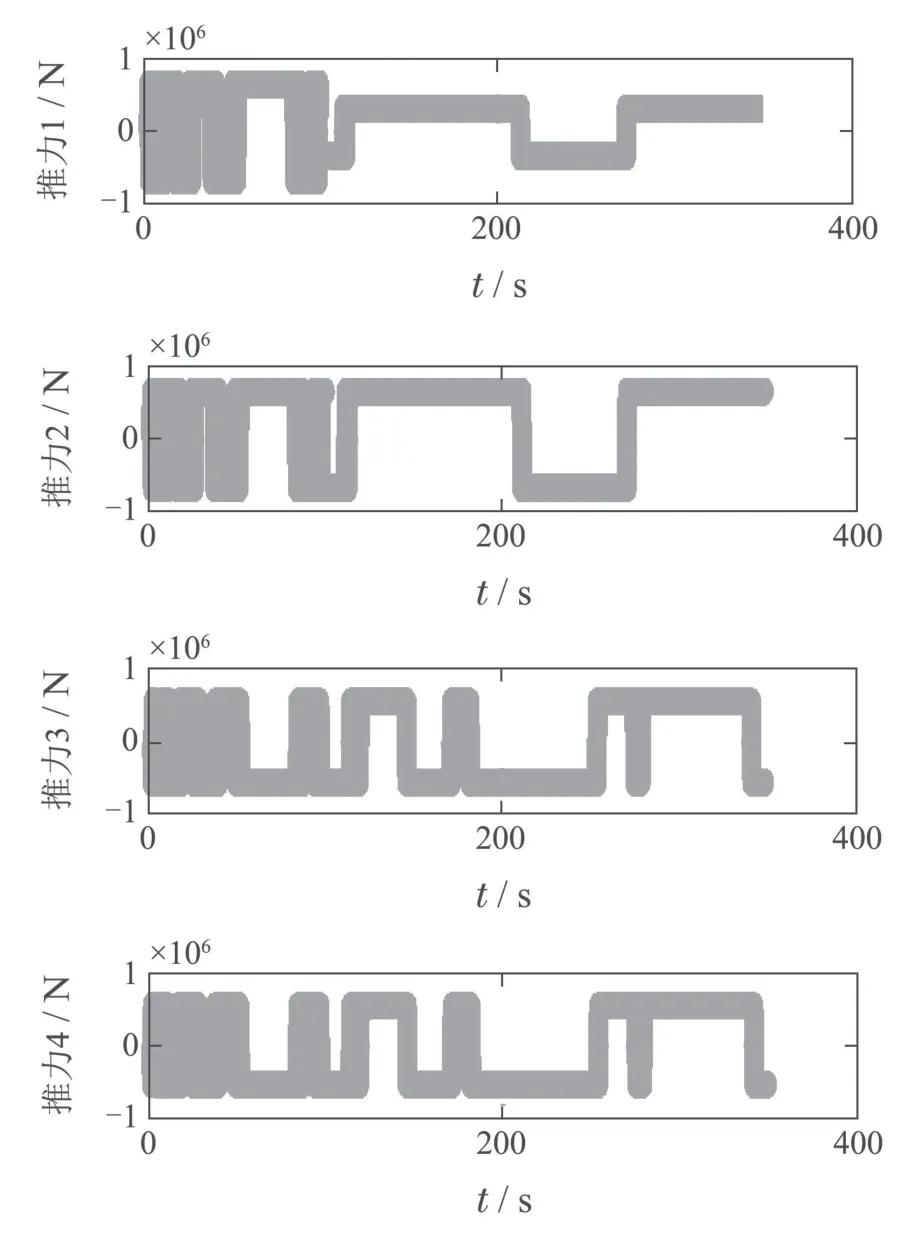
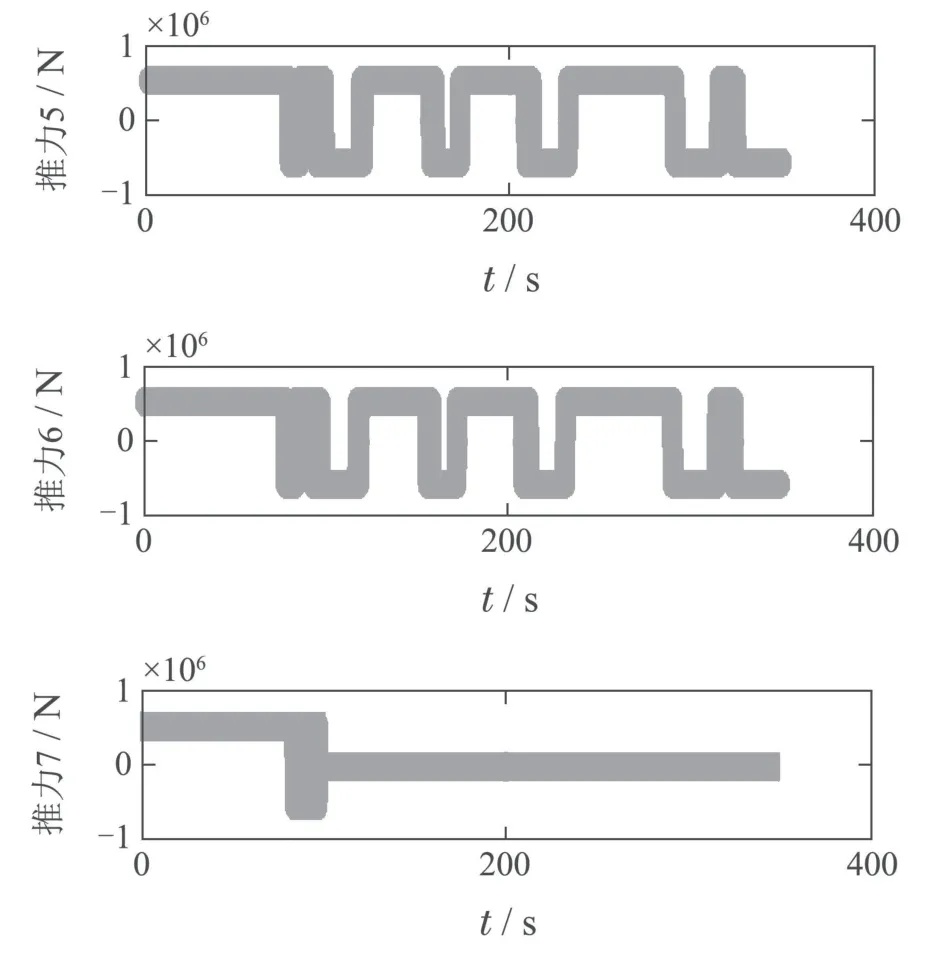
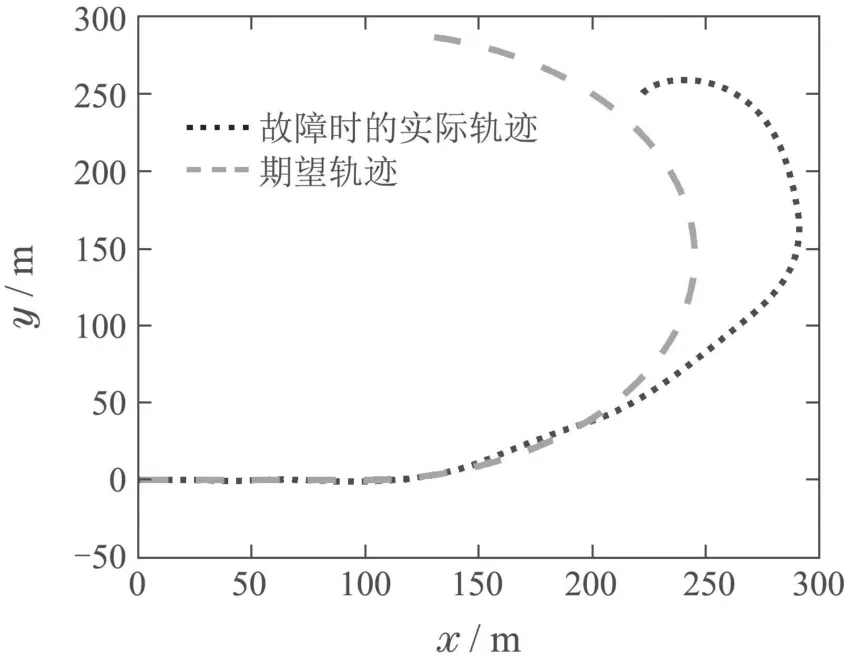
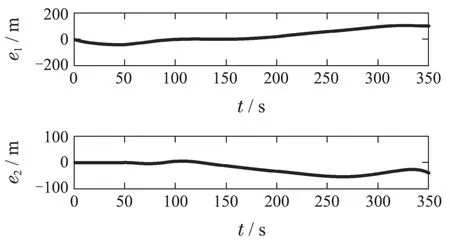
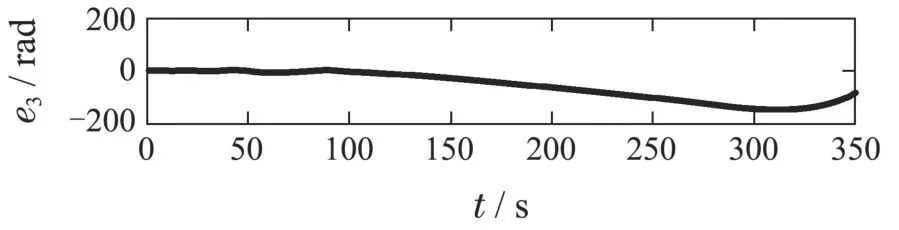
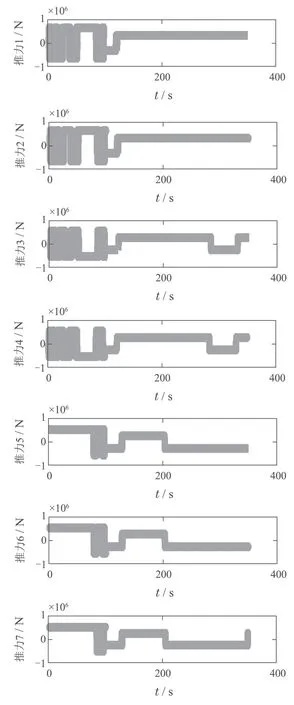
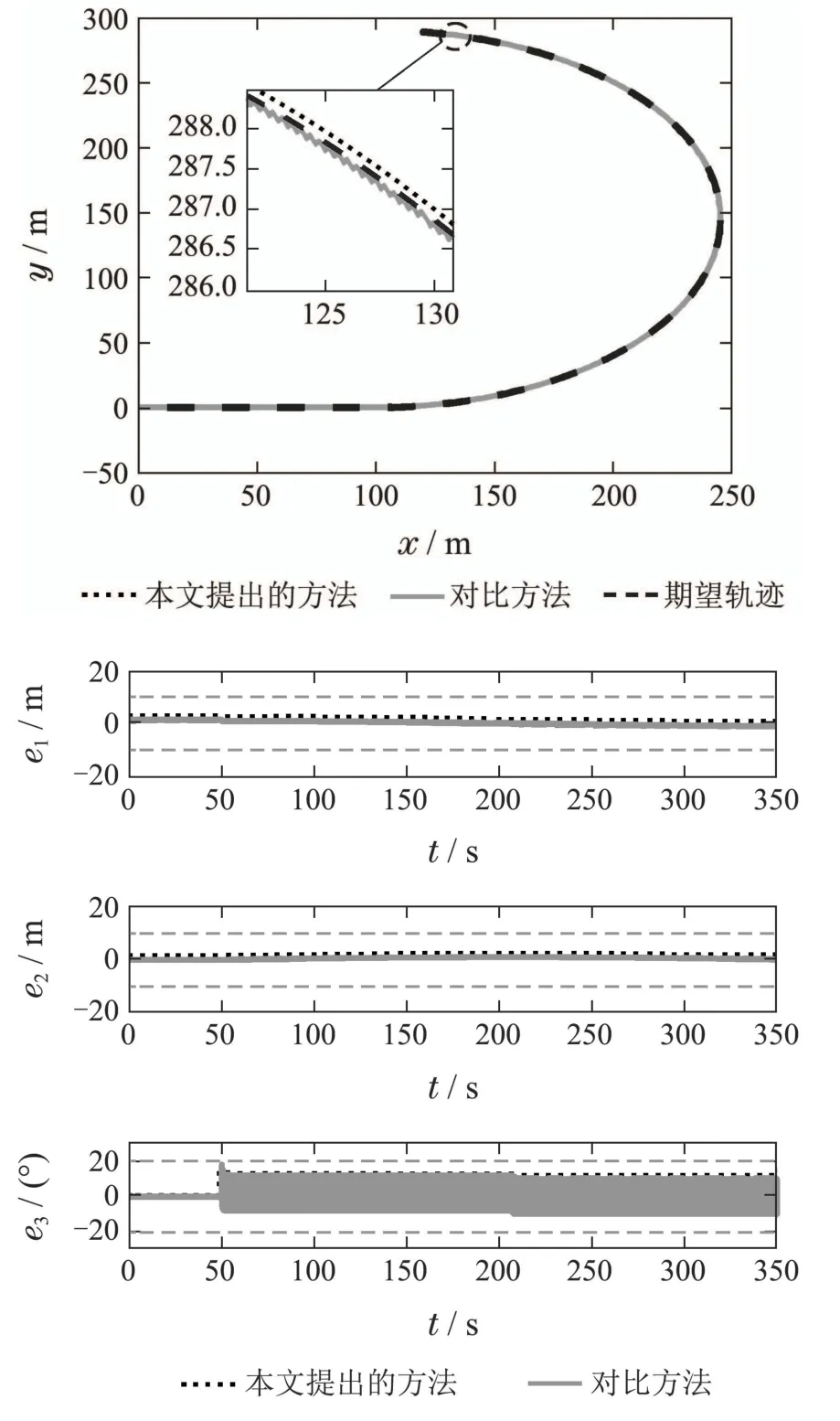
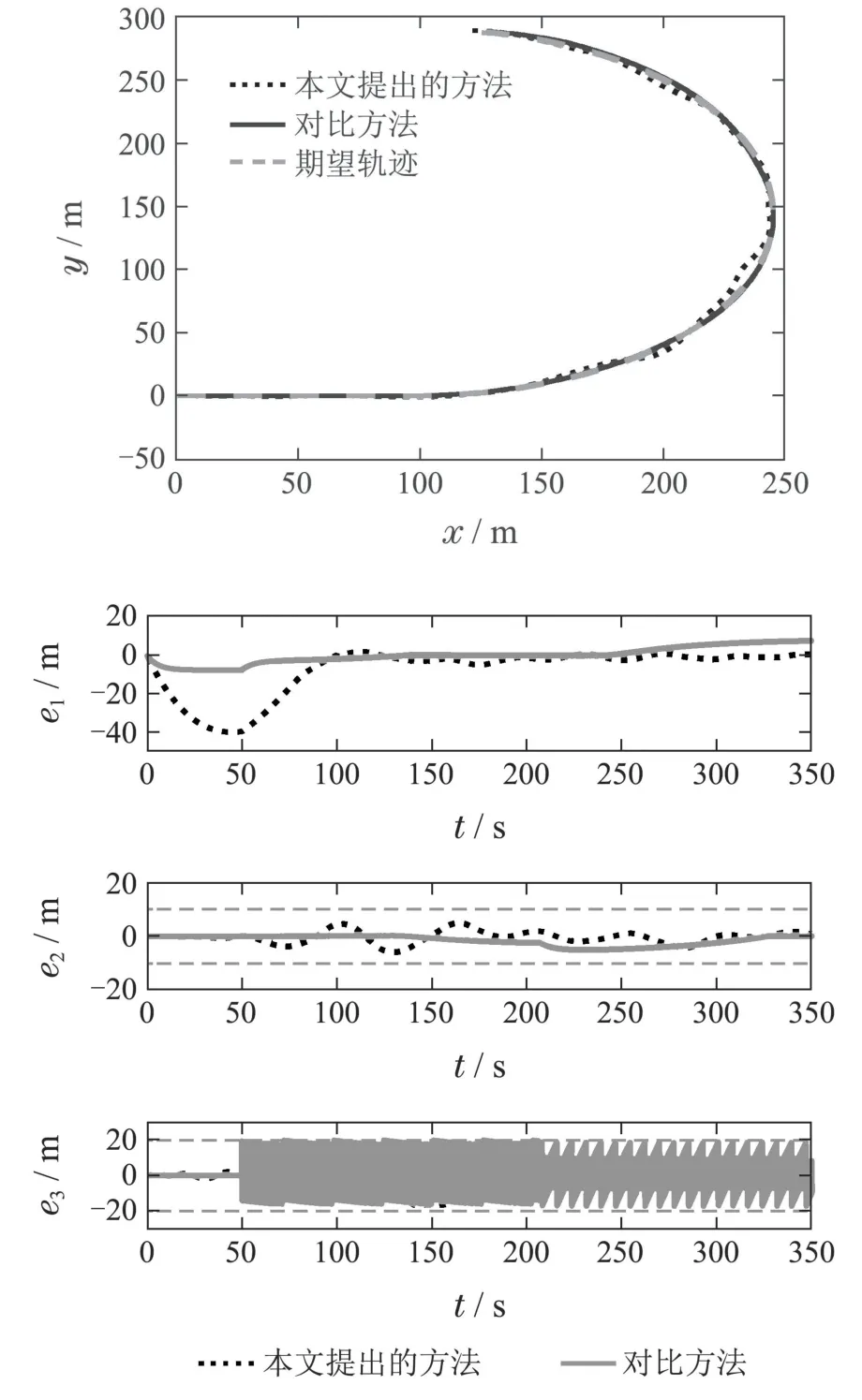
其中:k1,k2,k3表示的是控制器参数(正常数);a,b,g,h也是控制器参数(正整数)且满足不等式a/b 注4当>1时,根据s1是否接近平衡点,滑模面s1的一阶项或高阶项对于收敛速度分别起到了关键作用.因此,二阶快速非奇异终端滑模面可以提供更快的收敛速度.详细分析过程见附录. 对式(18)和式(19)分别求导如下: 结合方程(16)和式(17),对方程(23)进行化简得到 为了确保系统的稳定性,设计由符号函数构成的切换控制律τs: 因此,根据等效控制律(25)和切换控制律(26)得到最终控制律的导数 然而,对于动力定位船控制系统来讲,其中一个关键问题是系统中存在的不确定性包括了模型不确定性∆M,∆D以及时变干扰d(t),所以对于控制律(27),它在实际控制中并不适用.基于以上的原因,自适应神经网络控制引入到控制系统中,对于动力定位系统中存在的不确定项进行估计,其具体过程如下: 其中W∗表示的是控制系统中自适应神经网络方法中的权重向量,且满足等式方程代表了权重向量的估计而代表了权重向量的估计误差;κ(Z)表示的是逼近误差向量,Z[η ν]T是输入向量. 假设1κ(Z)表示的是有界逼近误差,即|κ(Z)|≤κm,κm为正常量. 综上,本文结合二阶快速非奇异终端滑模控制和自适应神经网络控制的理论思想,根据式(25)–(28)得到了如下动力定位船轨迹跟踪任务的控制律 同时,控制系统的自适应更新律为 其中Γ表示的是待设计的常值系数矩阵. 定理1考虑动力定位船在存在推进器故障以及模型不确定性前提下,由鲁棒容错控制器式(29)和自适应更新律式(30),确保系统在有限时间内到达滑模面s10和s20,同时保证闭环系统中的所有信号有界且位置和姿态跟踪误差e以指数的形式渐进收敛到微小邻域内,即收敛到期望轨迹. 此定理的证明可以通过以下步骤形成: 步骤1首先,定义一个Lyapunov函数V1如下: 计算V1的导数,同时将式(24)(28)和式(29)代入可得 步骤2其次,选取全局的Lyapunov函数V如下: 同样对函数V进行求导可以得到 将自适应更新律(30)代入式(34)可得 步骤3然后,如果k4>那么将会得到如下结果: 因此,根据式(36)的结果,显然可知s2是有界的.同理,根据滑模面的定义式(18)和式(19),滑模面s1和跟踪误差e显然也是有界的.此外,由于期望的轨迹ηd和是有界的,所以实际的轨迹η和速度ν同样有界. 步骤4最后,将式(36)进行变换得到如下结果: 根据式(37)和引理2可知,本文提出的控制器实现了闭环系统的一致稳定性,对于任何给定的初始条件,系统跟踪误差在有限时间内收敛到e0,并且收敛时间满足 注5为了能够将算法更好的用于实践任务之中,以伪代码的形式描述了该算法希望使其更容易融入相关的控制方案.改进的自适应滑模容错控制方法的实施过程如下: 5) 设计二阶滑模面: 6) 令s2=0,设计等效控制律τe(见式(25))和切换控制律τs(见式(26)); 7) 引入神经网络理论,进行系统不确定项的逼近(见式(28)): 8) 结合系统的故障模型(5),设计控制律(29)和自适应更新律(30):e →0; 9) end while 10)t=t+1; 11) end procedure 12) 实现动力定位船的轨迹跟踪任务. 本文的仿真模型参数来源于动力定位船“海洋石油201”,其具体的性能参数如表1所示. 表1 性能参数Table 1 Performance parameters 根据“海洋石油201”的物理参数以及性能参数,设置系统的初始状态为η(0)[0 0 0]T,ν(0)[0 0 0]T,同时可以获得以下动力学模型参数矩阵信息: 此外,“海洋石油201”的推进系统总共配有7个推进器,输出的最大推力分别为{680 kN,680 kN,540 kN,540 kN,540 kN,540 kN,540 kN},实际的位置分布如图2所示.因此根据其相关的位置分布信息可以得到推进器分布矩阵T如下: 图2 “海洋石油201”推进器布置图Fig.2 Thruster position of“Offshore Oil 201” 仿真时为了能够满足动力定位船的轨迹跟踪任务要求,设计了由直线和曲线连接共同组成的复杂期望轨迹ηd如下所示: 其中tet −50.仿真过程中设计了时变干扰函数 其中: 同时,在仿真的过程中设定推进器发生故障,其推进器故障(效率)矩阵设置为Fdiag{[1 1 1 1 1 1 0.4]}.相关控制器参数设置如下:t350 s,k1diag{[3.8 3.8 3.8]},k2diag{[1.5 1.5 1.5]},k3diag{[0.08 0.08 0.08]},k4diag{[0.8 0.8 0.8]},a0.9,b0.5,g0.6,h0.2,Γ1×106I729×729,权重向量的初值为i(0)0729×1(i1,2,3),仿真步长设置为0.05 s. 图3表示的是轨迹跟踪的具体情况,分别为存在推进器故障时的轨迹曲线、不存在推进器故障时的轨迹曲线以及期望的轨迹曲线.从图中不难发现,当不存在推进器故障时该方法可以很好地控制动力定位船进行轨迹跟踪任务,即使发生了推进器故障的问题,最终跟踪误差在所提出控制方法的作用下依然会收敛于原点附近的微小邻域而保证系统稳定,故该方法仍然能够保障动力定位船的跟踪效果.为了通过跟踪误差的描述能更好的说明跟踪情况,在仿真时设置符合任务要求的跟踪误差阈值为emax[10 10 20]T和emin[−10−10−20]T,通过图4分别给出了存在推进器故障以及不存在推进器故障情况下的跟踪误差,更直观的反映出虽然发生推进器故障时跟踪性能有所下降,但是依然能够实现跟踪的目标且能够满足误差阈值要求.此外,图5给出了轨迹跟踪过程中的详细状态响应曲线,包括了发生故障与否时的动力定位船的位置和姿态信息. 图3 轨迹跟踪的时间响应曲线Fig.3 Time response of the trajectory tracking 图4 跟踪误差的时间响应曲线Fig.4 Time response of the tracking error 图5 位置和姿态的时间响应曲线Fig.5 Time response of the position and posture 图6和图7为控制器中设计的比例微分滑模面(s1)和快速非奇异终端滑模面(s2)的时间响应曲线,从图中可以看出控制系统的状态轨迹在不产生抖振的情况下运动到滑模面上,同时保证跟踪误差快速收敛到微小邻域内.图8表示的是神经网络控制器权重范数的时间响应曲线,从图中可以看到该状态量在故障存在的前提下最终实现稳定. 图6 比例微分滑模面时间响应曲线Fig.6 Time response of proportional-derivative sliding mode manifold 图7 快速非奇异终端滑模面时间响应曲线Fig.7 Time response of fast nonsingular terminal sliding mode manifold 图8 自适应更新律范数的时间响应曲线Fig.8 Time response of norm of adaptive update law 图9为动力定位船的推进系统的实际控制输出响应曲线.从图中可以看出,曲线的变化满足“海洋石油201”动力定位船推进系统的物理约束,同时该方法保证了整个推力的曲线虽然有波动却没有严重的抖振现象,而且能够较好的保证闭环系统的控制性能. 图9 推进器控制输出的时间响应曲线Fig.9 Time response of control force outputs of the thrusters 除此之外,为了模拟本文提出方法在实际工程中所遇到的推进器故障情况,因此主要分成3种情况进行了以下讨论: 情况1设置推进器故障(效率)矩阵为Fdiag{[1 1 0.5 0.5 1 1 1]}时,其轨迹跟踪相关情况如图10–12所示. 图10 当F=diag{[1 1 0.5 0.5 1 1 1]}时的轨迹跟踪曲线Fig.10 Trajectory tracking curve when F=diag{[1 1 0.5 0.5 1 1 1]} 图11 当F=diag{[1 1 0.5 0.5 1 1 1]}时的跟踪误差曲线Fig.11 The tracking error curve when F=diag{[1 1 0.5 0.5 1 1 1]} 图12 当F=diag{[1 1 0.5 0.5 1 1 1]}时的控制输出曲线Fig.12 Control outputs curve when F=diag{[1 1 0.5 0.5 1 1 1]} 情况2设置推进器故障(效率)矩阵为Fdiag{[0.5 1 1 1 1 1 0]}时,其轨迹跟踪相关情况如图13–15所示. 图13 当F=diag{[0.5 1 1 1 1 1 0]}时的轨迹跟踪曲线Fig.13 Trajectory tracking curve when F=diag{[0.5 1 1 1 1 1 0]} 图14 当F=diag{[0.5 1 1 1 1 1 0]}时的跟踪误差曲线Fig.14 The tracking error curve when F=diag{[0.5 1 1 1 1 0]} 图15 当F=diag{[0.5 1 1 1 1 1 0]}时的控制输出曲线Fig.15 Control outputs curve when F=diag{[0.5 1 1 1 1 1 0]} 情况3设置推进器故障(效率)矩阵为 Fdiag{[0.5 0.5 0.5 0.5 0.5 0.5 0.5]}时,其轨迹跟踪相关情况如图16–18所示. 图16 当F=diag{[0.5 0.5 0.5 0.5 0.5 0.5 0.5]}时的轨迹跟踪曲线Fig.16 Trajectory tracking curve when F=diag{[0.5 0.5 0.5 0.5 0.5 0.5 0.5]} 图17 当F=diag{[0.5 0.5 0.5 0.5 0.5 0.5 0.5]}时的跟踪误差曲线Fig.17 The tracking error curve when F=diag{[0.5 0.5 0.5 0.5 0.5 0.5 0.5]} 图18 当F=diag{[0.5 0.5 0.5 0.5 0.5 0.5 0.5]}时的控制输出曲线Fig.18 Control outputs curve when F=diag{[0.5 0.5 0.5 0.5 0.5 0.5 0.5]} 根据情况1–3中的轨迹跟踪相关结果可知,本文提出的方法对于推进器故障的容错能力依然存在的一定的裕度和限制.情况1和情况2的情况下虽然也能够维持轨迹跟踪的任务,但是已经出现了较大的跟踪误差,无法执行较为严格的轨迹跟踪任务.情况3中的设定为所有的推进器只能够提供一半的推力,即模拟整个推进系统有一半的推进器发生故障,因此视为较为严重的推进器故障情况,由图16−18可知在这种情况下已经无法完成要求的轨迹跟踪情况.对于更为复杂的推力分配与优化问题,将是后续研究工作的重点内容. 为了能够更好的说明本文提出的控制器的控制效果,选取了文献[33]中的非奇异快速终端滑模控制方法作为对比,得到了如图19和图20的轨迹跟踪情况,其中对比控制器结构如下所示: 图19 无故障时的轨迹跟踪情况对比Fig.19 Comparison of trajectory tracking when no fault 图20 故障时的轨迹跟踪情况对比Fig.20 Comparison of trajectory tracking when faults 通过不断地仿真调试得到对比控制器的仿真参数如表2所示. 表2 对比控制器的仿真参数Table 2 The simulation parameters of compared controller 图19和图20分别表示的是存在故障以及无故障发生时的动力定位船的轨迹跟踪曲线以及跟踪误差曲线,从图中可以看出在无故障发生时,两控制器都能满足跟踪任务的要求和约束,当有推进器故障发生时,推力下降受到输入饱和问题的限制,误差曲线产生了一定的波动但最终都会满足红色的误差约束的限制.此外,对比控制器无论故障发生与否的轨迹跟踪过程中都存在着明显的抖振问题,这会严重的影响推进器的物理寿命,因此在实际工程中应尽量的避免,本文提出的控制器与对比控制器的显著提升在于,解决了控制过程中的抖振问题,这样更能保证本文提出控制方法的实用性和有效性. 本文研究了动力定位船在存在模型不确定性和时变干扰以及推进器故障情况下的轨迹跟踪问题.首先给出了简化的三自由度模型,提出了一种新颖的改进二阶非奇异快速终端滑模容错控制器,保证了轨迹跟踪过程中系统的鲁棒性,同时解决了传统滑模控制方法的奇异和抖振的问题,而且提高了收敛速度实现了有限时间收敛.然后,为了解决系统模型的不确定性引入了自适应神经网络算法,利用RBF神经网络逼近并补偿不确定项.最后,利用Lyapunov函数证明了系统的稳定性,通过仿真实验和模拟案例验证了所提方法的可行性.在未来的研究中,将会把预设性能控制的思想引入控制器,保证控制系统的暂态性能和稳态性能,同时引入“绿色DP”的概念,实现动力定位船推力系统的优化. 附录 对于注4的解释:为了验证本文提出的方法能够提供更快的收敛速度,选取传统的二阶滑模方法作为对比,其滑模面的构成如下所示: 式中的参数设计与本文相同,e表示跟踪误差,k1,k3表示正常量,a,b表示正整数且满足a/b>1. 那么当状态轨迹到达滑模面c2上,即c2(t)=0,则有如下等式成立: 同时,c1收敛到平衡点的收敛时间tc可以表示为 相比于传统的二阶滑模,本文提出的二阶快速非奇异终端滑模面如下: 其中:e,k1,k3,a,b选取与上面相同的参数,k2为正常量,g,h同样为正整数且满足g/h>a/b. 同样参数情况下,当状态轨迹到达滑模面s2上,即s2(t)=0,则有如下等式成立: 因为g/h>a/b>1,所以当s1离平衡点较远时,s1的高阶项对于收敛的速度影响较大起主要作用,因此可以将式(A4)近似约等于 显而易见,与式(A1)中的c1相比,式(A4)中的s1具有更快的收敛速率. 此外,当s1离平衡点较近时,s1的一阶项对于收敛的速度影响较大并起主要作用,因此可以忽略其高阶项的影响将式(A4)近似约等于 显然,c1与s1具有相同的收敛速率. 更进一步,由方程(A4)可知,s1收敛到平衡点的收敛时间ts可以表示为 比较式(A2)和式(A7),其中g/h>a/b>1,所以 因此可以得到 综上所述,本文提出的SOFNTSM滑模面可以提供更快的收敛速度.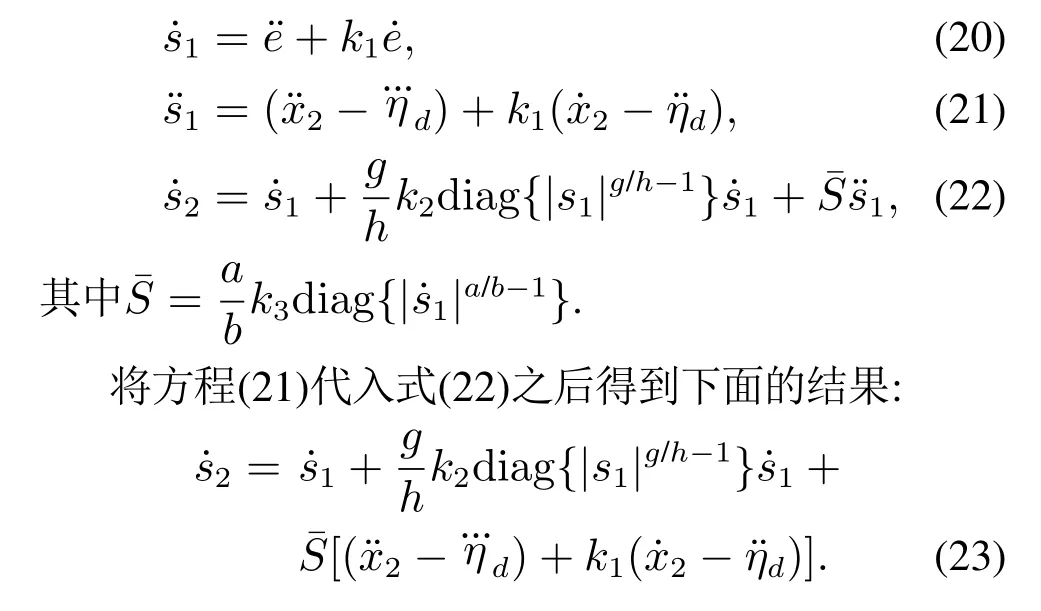


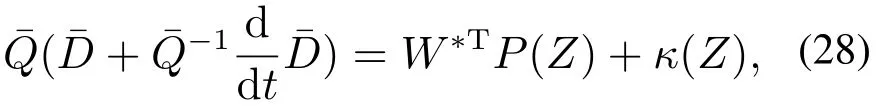
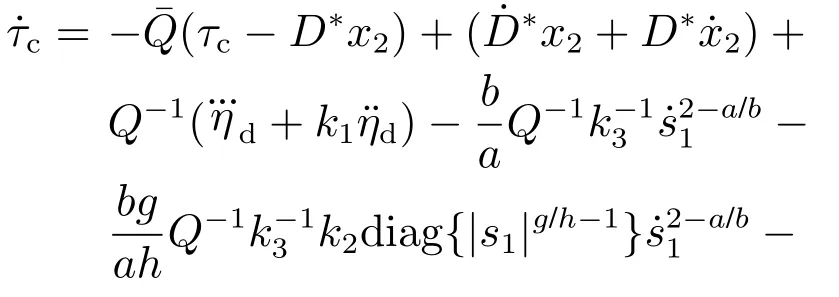

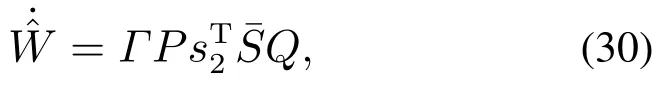


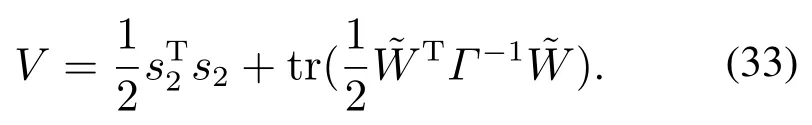
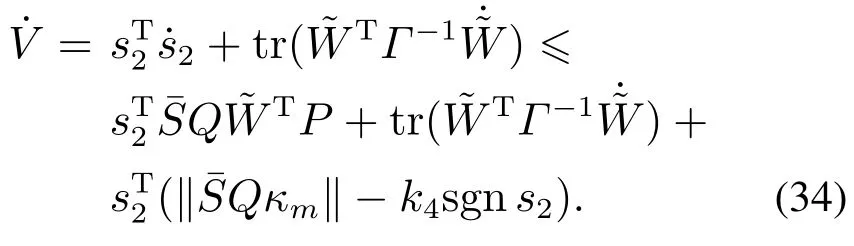
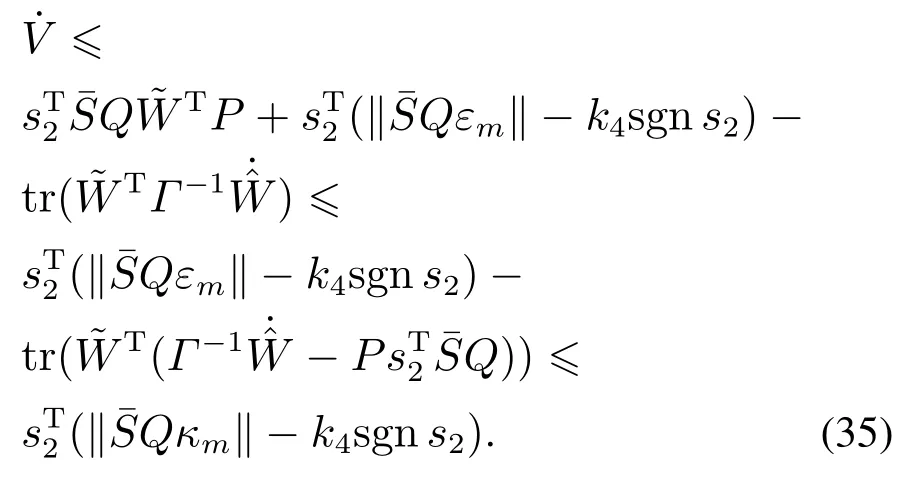
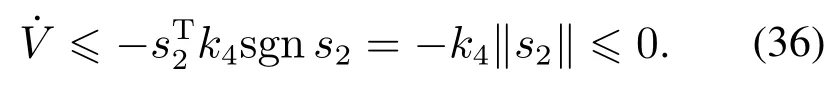
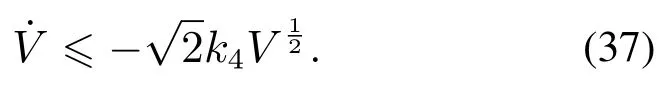
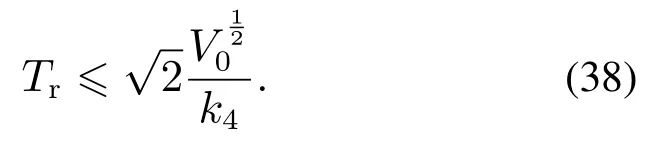


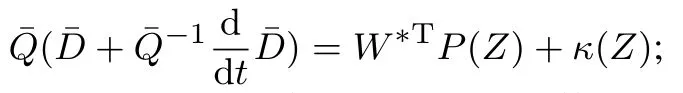
4 数值仿真实验
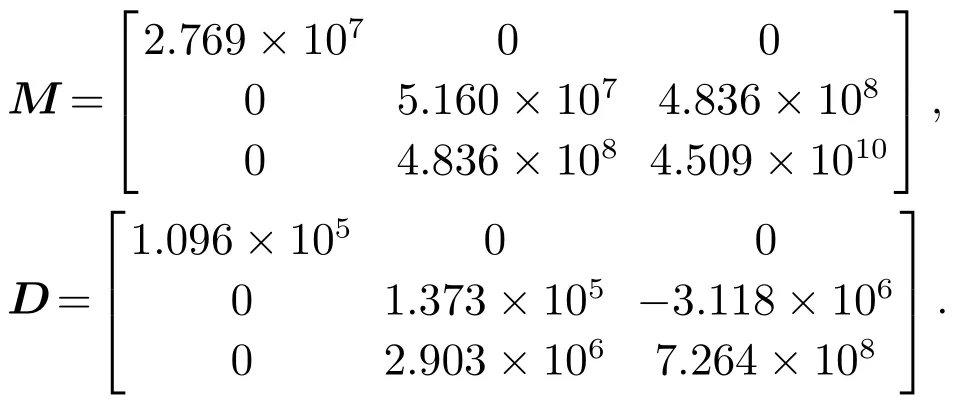
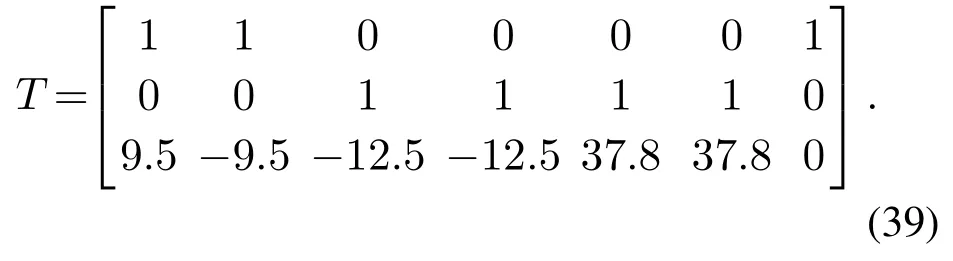
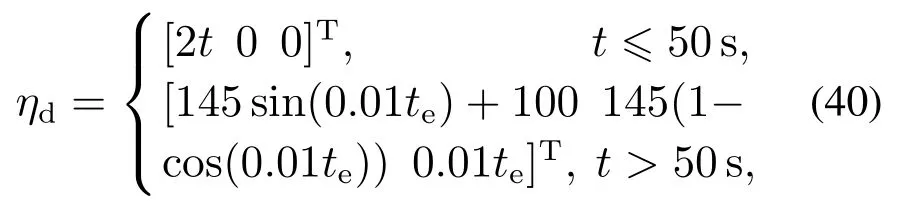
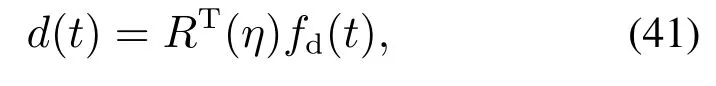



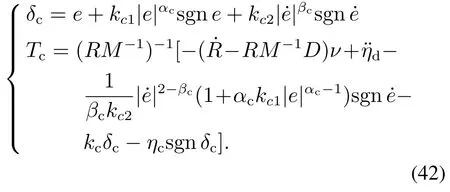

5 结论