基于可靠性的车辆防护组件优化*

吴 凯，王显会，周云波，毕 政，李明星

（南京理工大学机械工程学院，江苏 南京210094）

在非对称局部战争的环境下，简易爆炸装置（improvised explosive device,IED）及地雷的威胁日益增大，军用车辆自身的防护及作战能力需得到更大的提升[1]。防地雷反伏击车主要通过底部防护组件来抵挡地雷和简易爆炸装置的威胁，防雷组件的厚度及质量的增加能在一定程度上提升车辆防护性能，但同时也会影响车辆的机动性。因此，在确保车辆防护能力的同时对底部防护组件进行轻量化设计是必要的。然而，在优化设计过程中，设计变量的不确定性以及爆炸工况的不确定性会影响目标性能，如防护组件的厚度变化、材料性能变化、爆炸环境下的土壤密度和炸药当量的变化等，这些设计变量的波动可能会导致最终设计失败，因此需在优化设计过程中引入可靠性优化。

对传统车辆碰撞安全性能的优化，已有了大量可靠性优化研究。吕晓江等[2]将多目标可靠性优化分析应用到一种车型正面40%重叠可变型壁障碰撞中，达到了车辆耐撞性和轻量化的要求，并提高了车身设计的可靠性。Pan 等[3]通过补偿代理模型拟合误差的保守策略，在车辆正面碰撞的可靠性优化中实现了可行的最佳设计。陈崇等[4]提出一种综合量化多种不确定性的概率统计方法，并将它运用在车辆前纵梁的稳健性设计中，实现了轻量化。Gu 等[5]在车辆前部结构耐撞性设计中，分别对比了确定性、可靠性和稳健性多目标优化，说明通过不确定性优化可以显著提高设计的可靠性和稳健性。在车辆爆炸防护领域，相关研究仅限于确定性优化。魏然等[6]对一种防护型车辆底部结构和乘员系统进行多参数优化，引入降维技术，不仅缩减了样本空间，而且提高了优化的精度。李明星等[7]通过径向基函数构建神经网络代理模型，并应用多目标遗传算法，对V 型防护组件进行优化设计，通过实验验证了该手段的可行性。

在本文中，提出车辆底部防护结构的多目标可靠性优化流程，考虑结构尺寸的不确定性，同时引入多种材料的离散变量，再通过灵敏度分析完成设计变量的筛选，构造并选择合适的代理模型进行结构的可靠性优化，并与确定性优化结果进行对比，拟为车辆防护提供可靠的设计方案和建议。

1 优化理论

1.1 确定性多目标优化

传统的多目标优化基本为确定性多目标优化，此类问题的数学模型通常为：

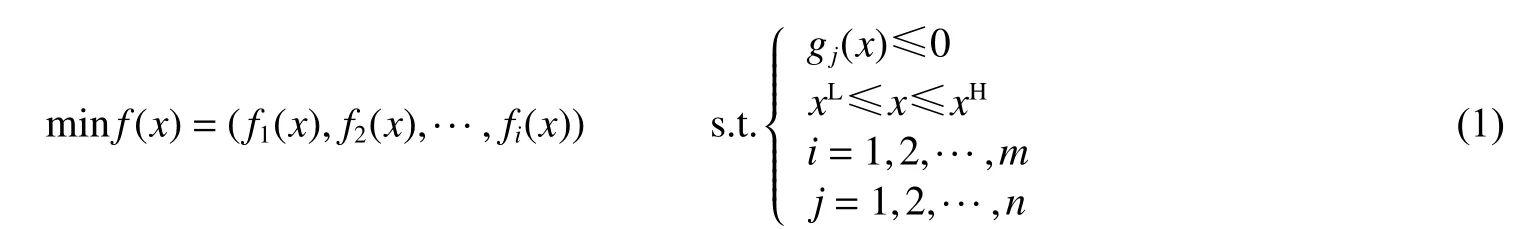
式中：fi(x)为设计目标，gj(x)为约束函数，m为目标的数量，n为约束的数量，xL和xH分别为设计变量x 的下限和上限。

工程实践中已广泛运用这类优化方法，但该方法所得结果易将有些设计变量取为约束边界值，导致对设计参数过于敏感。设计参数的变化会导致设计目标的严重性能损失，使设计变得不可靠[8]。在实际工程问题中，常存在一些不确定因素，如材料尺寸、材料性能、载荷偏差等，而确定性优化在设计初期未考虑这些因素，因此得到的优化结果与实际应用中的效果可能相差较大，甚至无法满足设计要求[9]。

1.2 可靠性多目标优化

与确定性多目标优化不同，可靠性多目标优化在设计前期就考虑了多种不确定因素，数学模型为：

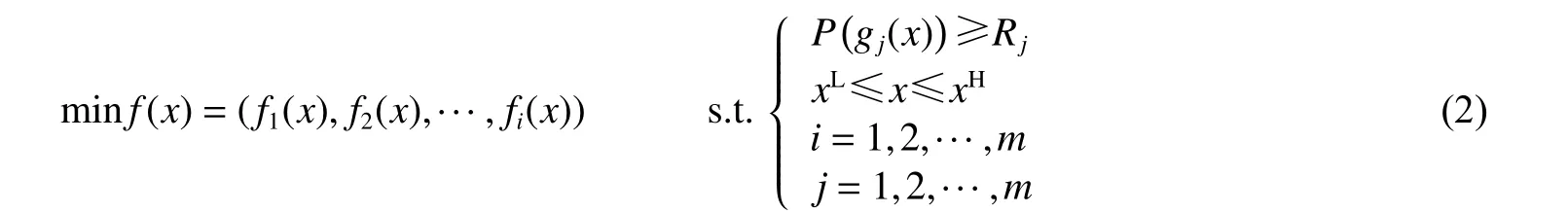
式中：fi(x)和gj(x)分别为目标函数和约束函数，x 为设计变量，Rj为满足约束gj(x)的期望可靠度（设计失败，gj(x)＞0）。

在工程设计中，可靠性可以定义为满足约束的概率，图1为确定性设计和可靠性设计的函数分布。可以看出，确定性优化的目标函数曲线存在不满足约束的值，在实际应用中当设计变量取到正态分布边界值时，对应目标函数将无法满足约束，导致设计失败。而可靠性设计中，设计变量对应的目标函数偏离约束较远，设计具有较高的可靠性。在爆炸防护设计中，不可靠的设计可能会导致人员的严重损伤，因此需引入可靠性优化设计。

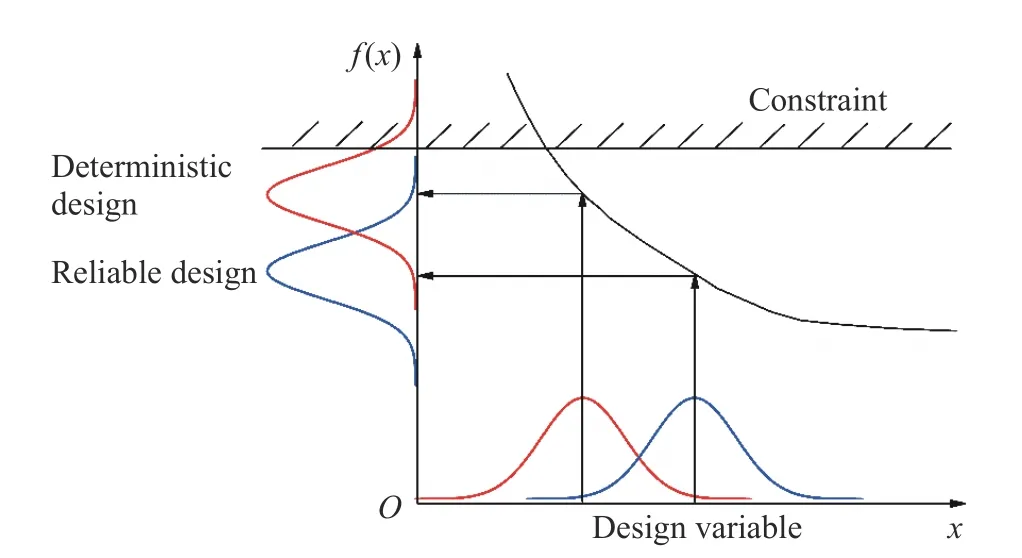
图1 可靠性设计的偏移Fig.1 Reliability design offsets

1.3 优化流程

针对多变量与强非线性的车辆防护组件防护性及轻量化设计，引入可靠性优化设计方法[10]，主要流程如图2所示。

建立有限元模型和实验验证，并将两者结果进行对比，验证模型精确性后开展后续优化流程。先定义优化问题，根据优化问题确定设计变量和优化目标函数，并定义各变量的取值范围和概率分布。通过优化拉丁超立方实验设计生成第一轮样本点，计算后得到对应响应，结合方差灵敏度分析方法完成设计变量的筛选。筛选变量后进行三类代理模型的构建拟合，比较并选择精确度最高的代理模型进行多目标优化，再采用蒙特卡洛方法进行可靠性分析得到可靠性优化结果[11]。

图2 可靠性优化流程Fig.2 Reliability optimization flowchart

2 模型验证

2.1 底部防护组件台架实验

代表设计状态的车辆底部防护组件和代表车辆乘员舱底板状态的基板，参照北约AEP-55—2011《Procedures for evaluating the protection level of armored vehicles:mine threat,Vol.2》中的2b实验，爆炸物（6 kg TNT当量）位于台架底部正中心位置，掩埋于硬质土壤表面下100 mm 处。

在实际测量中，将基板表面网格化，以便精确测量实验后基板的变形，并且和模拟进行对比。组件实验装置如图3所示。

图3 台架爆炸实验Fig.3 Platform explosion experiment

2.2 车辆底部防护组件模型

为了比较车辆底部爆炸防护性能，设计了三明治夹层结构防护组件，防护组件主要由三层结构组成：上层为单面板，中间夹层包括蜂窝铝和横纵工字梁，底部面板为单层平板。防护组件整体尺寸为1 860 mm×1 500 mm×118 mm，防护组件底面离地高度为337 mm，组件上方进行铁块配重，配重后整体质量为9 011 kg，初始模型面板材料均为6252型防弹钢，加强梁材料为BS700型钢，材料本构模型选用Johnson-Cook 模型。

参照AEP-55—2011中的2b实验，设置模型炸药当量为6 kg，炸药掩埋深度为100 mm。防护组件台架模型如图4所示，模型主要由防护组件、配重、台架、空气域、土壤、炸药组成[12]。在有限元模拟中，一定程度上减小网格尺寸和增加网格数量将提升计算精度，但需要更大的计算成本。综合考虑计算效率和精度，网格单元大小主要分布在10～20 mm，其中组件内部蜂窝铝结构的网格单元大小为4 mm。空气和土壤由六面体网格划分，其余部件均由壳单元组成。在计算过程中，伪应变能占总内能比的2.3%，小于5%，满足模拟有效性要求。

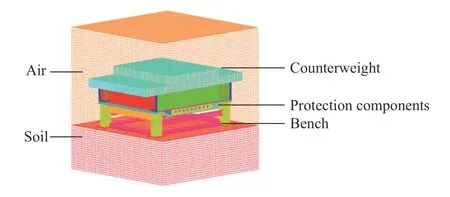
图4 台架的有限元模型Fig.4 Finite element model of platform

2.3 模型有效性验证

为确保后续优化工作的有效性[13]，需对初始有限元模型进行准确性验证，比较模拟结果与实验结果，模型准确度主要通过比对组件基板最大变形量和组件整体变形情况来衡量。

实验后的基板变形状态如图5（a）所示，可以看到，基板呈双峰状变形，整体为上凸变形，中心局部区域存在凹陷情况，表面存在较多不规则凹陷，整体未出现大面积破裂。模拟的基板变形情况如图5（b）所示，与实验基本相符。实验前在基板上标记变形测量点，实验后以基板安装点为基准，横向等距取20个塑性变形量最大的点进行测量，实验和模拟的测量点塑性变形量曲线如图5（c）所示。两条曲线基本吻合，实验的基板最大塑性变形为190 mm，模拟的为185.9 mm，误差小于5%，满足模拟精度要求。但防护组件整体防护性能仍未达到要求，基板最大塑性变形量达到了190 mm，远超出了100 m 的设计要求，且组件整体质量过大，需进行优化设计。

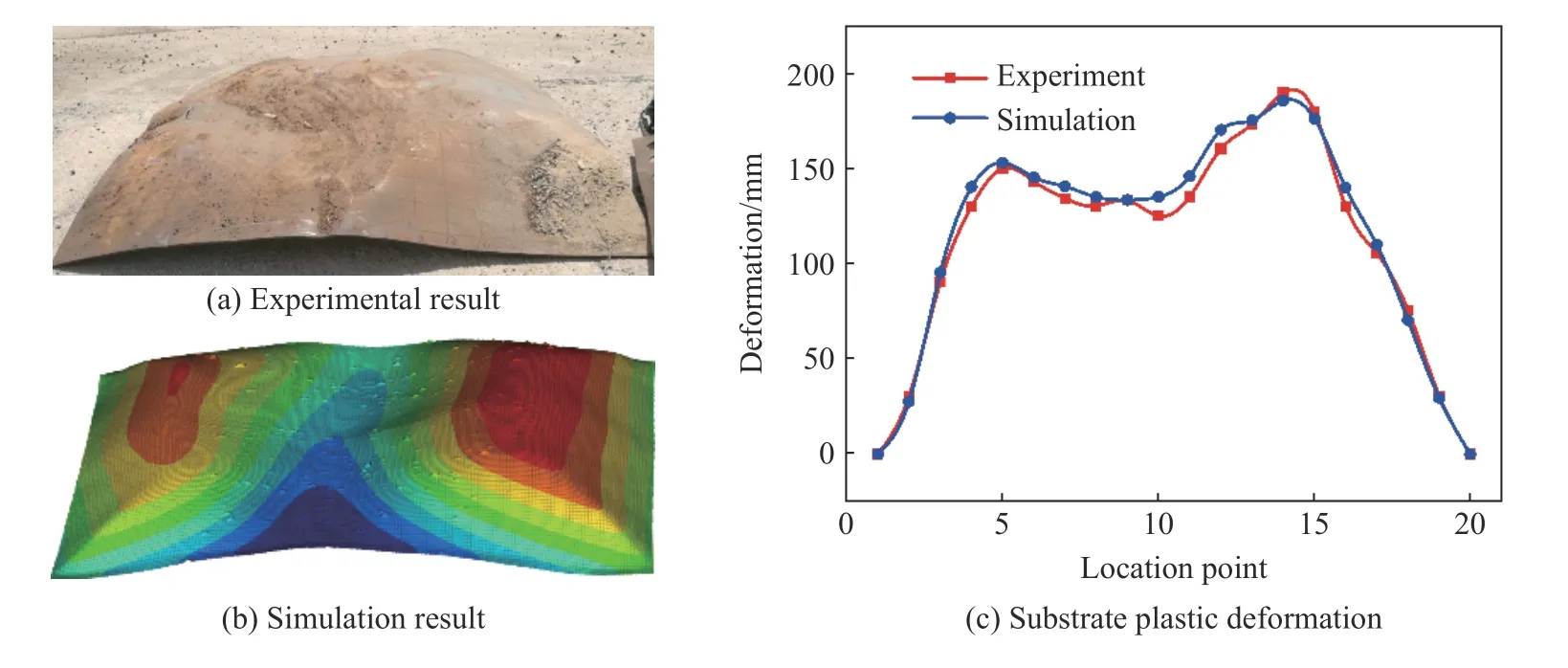
图5 基板变形对比Fig.5 Comparison of substrate deformations

3 优化设计

3.1 设计变量及目标的定义

整体模型共包含23 个部件、1 333 851个单元、1 087 626个节点，配重后质量为9 000 kg。由图6可见，爆炸冲击后，防护组件基板在约7 ms达到最大变形，爆炸模拟计算至50 ms即可得到最大塑性变形。使用i7 CPU、8 GB内存的电脑计算，时长约为10 h。

在整车中，防护组件与车体之间的作用关系可用基板变形来衡量，同时在设计中应考虑轻量化。当前仅为台架实验，没有整车实验中的假人各项损伤指标作为约束。针对要求，选取防护组件质量M 和基板最大塑性变形量D 作为设计目标，初始值和目标见表1，唯一约束为基板最大塑性变形量。

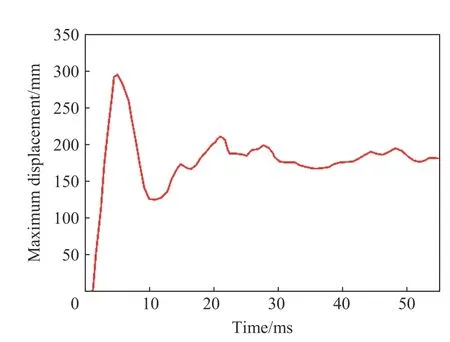
图6 基板最大位移Fig.6 Maximum displacement of substrate

表1 设计目标和初始值Table 1 Design goals and initial values

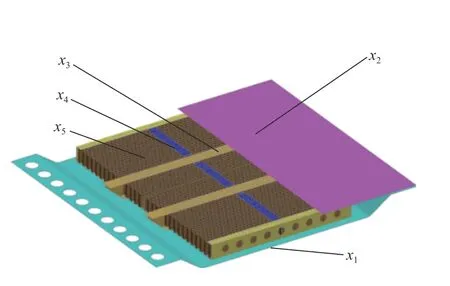
图7 设计变量位置Fig.7 Positions of design variables

防护组件整体部件参数并不多，因此在初期代理模型构建时选取所有可更改参数的目标变量，共计11个设计变量，变量位置如图7所示。其中：5个为连续变量（面板厚度x1，背板厚度x2，横梁厚度x3，纵梁厚度x4，蜂窝胞元厚度x5）；6 个为离散变量（纵梁数x6，横梁数x7，横纵梁材料x8，背板材料x9，面板材料x10，蜂窝材料x11）。变量x1～x5均为连续型数值变量；变量x6取为1、2，变量x7取为1、2、3，对应六类防护组件基础模型，有限元模型如图8所示；变量x8～x11均为离散型材料变量，待选材料20种。因加工工艺限制，横梁、纵梁材料可选变量数为12种，背板材料可选变量数为15种，面板材料可选变量数为11种，蜂窝材料可选变量数为15种，选则范围和分布系数根据实际工程应用情况决定，见表2。各材料具体参数见表3。

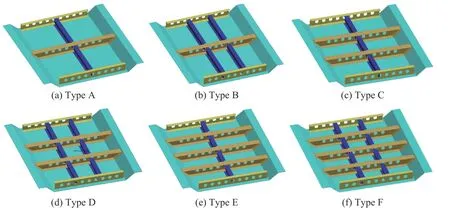
图8 梁组合类型Fig.8 Beam combination types

根据所选取的设计变量和设计目标，可得数学模型：

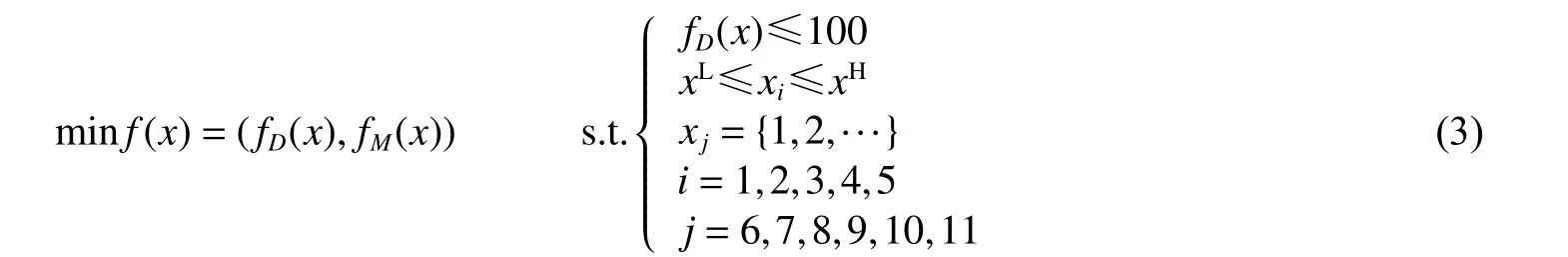
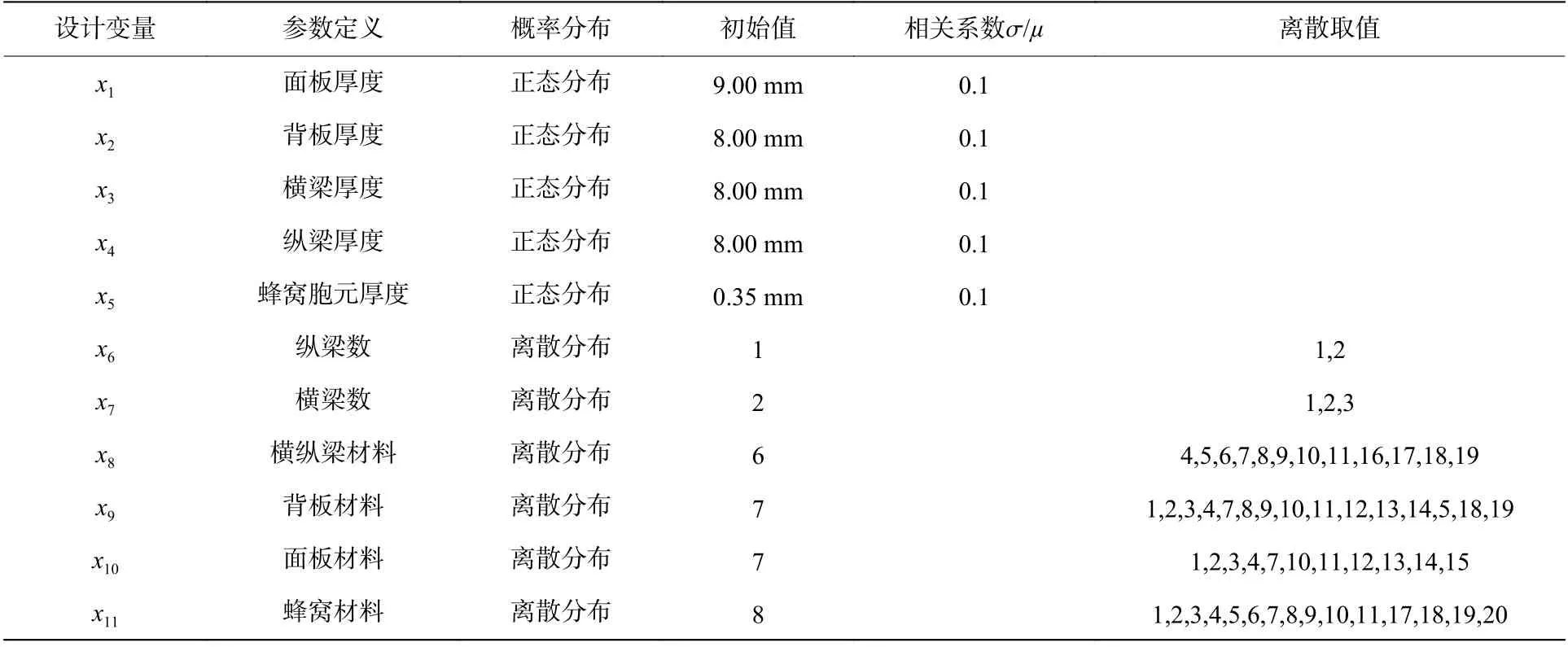
表2 设计变量的初始值和概率分布Table 2 Initial valuesand probability distributions of design variables

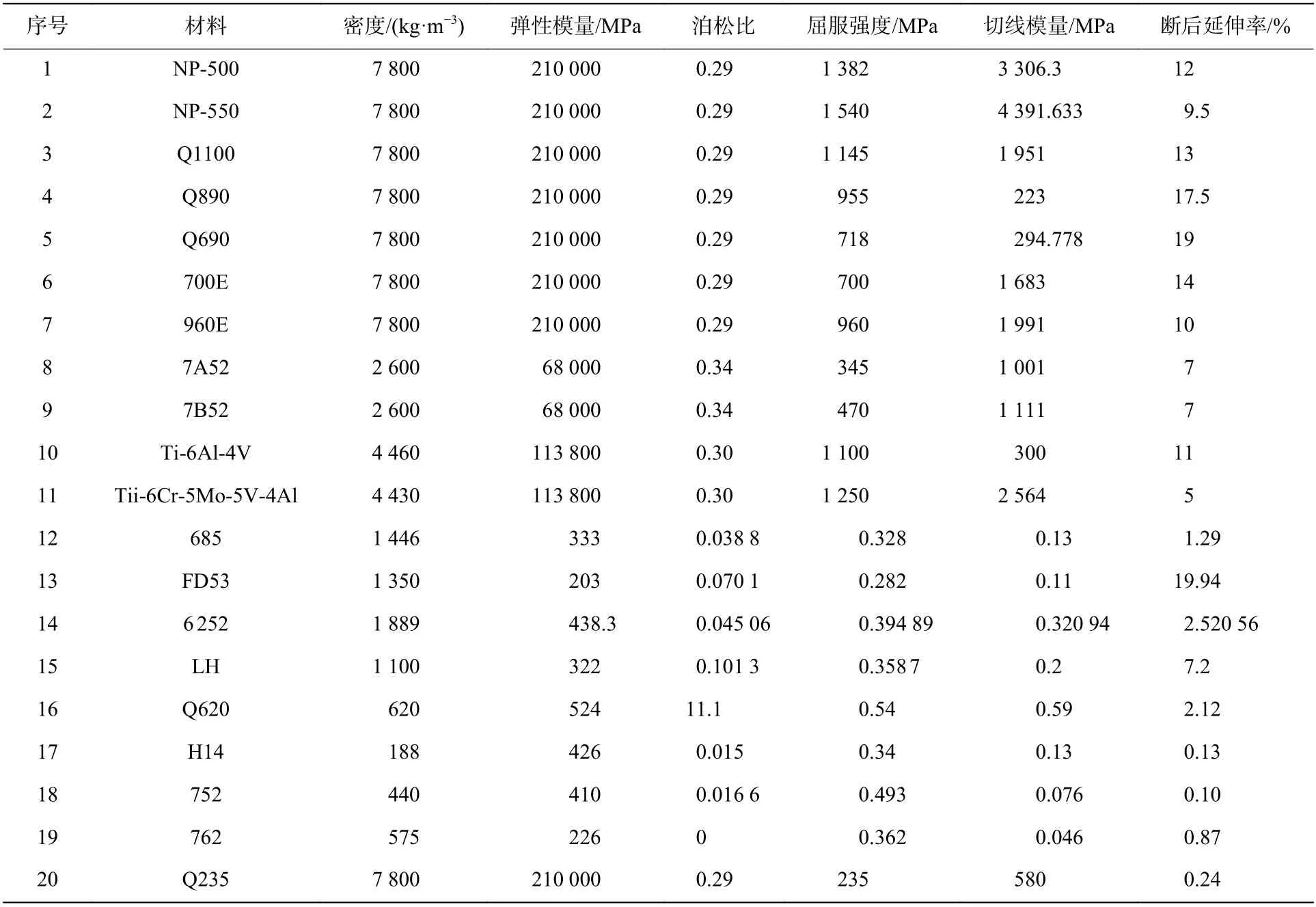
表3 材料参数Table 3 Material parameters

3.2 设计变量的筛选

优化拉丁超立方采样允许更多的点和更多的组合，且实验点分布均匀，可以捕捉到更高阶的效果，兼具了均匀采样和拉丁超立方采样的优点。本文中，设计采样过程选择优化拉丁超立方实验设计方法，对11个设计变量进行空间均匀填充，第1次采样样本点数量为120 个，部分样本点数据见表4。

表4 优化拉丁超立方采样样本Table 4 Optimization of Latin hypercube samples

通过对上述120组样本点的计算，得到对应响应，运用方差分析（ANOVA）方法得到11个变量对2个设计目标的累积贡献度，如图9所示。在所有设计变量中，x3、x6、x11、x7、x4、x8对设计目标的累积贡献度较低，主要为防护结构中间夹层中的横纵梁数量和厚度及蜂窝材料。设计变量数量的增多易降低代理模型的精确度[14]，因此在后续设计过程中将上述低贡献度变量设置为初始值。

3.3 代理模型拟合及选择

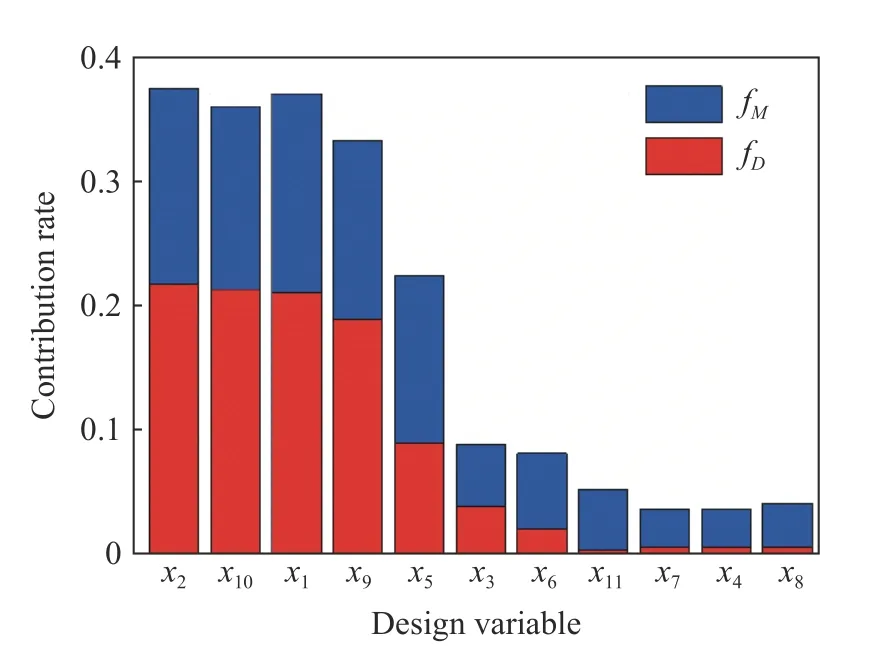
图9 设计变量的贡献Fig.9 Contributionsof design variables

通常，单个有限元模型的计算量非常大，如直接基于数值模型进行结构优化设计，则计算资源负担巨大、效率极低，在工程上不可行。因此，需引入代理模型的概念，即根据输入（实验设计生成的设计变量集）与输出（对应的目标响应）之间的关系构建模型[15]。代理模型可以高效地预测在设计空间内其他点的响应，已被广泛运用于结构优化设计中[16]。但不同的代理模型构建方法所适用的对象不尽相同，本文中将应用三种不同的代理模型，并对比分析各代理模型的精度，选用最合适的模型。

响应面模型（response surfacemethod,RSM）的构建较简单，它选取合适的基函数，建立设计变量与目标之间的近似关系，常用的近似方法为基于多项式基函数的多项式响应面法。该方法虽然较易获得显式的数学表达式，但对高度非线性的系统精度不高。

径向基函数模型（radial basis function,RBF）是一种单隐层的前馈神经网络，接收输入信号的单元层为输入层，输入信号通过传递函数映射到隐含层，将输入矢量直接映射到一个新的空间。RBF逼近具有训练速度快、网络结构紧凑等特点。该方法计算量相对较少，较适用多变量、非线性系统。

克里金模型（Kriging,KRG）是一种建立在变异函数理论基础上的半参数化近似模型，是一种空间局部插值法。通过已知的采样点数据，对估计样本点数据进行动态的选择和筛选，并对所选择的样本点进行拟合，具有全局和局部统计特性，对于非线性程度较高的系统有较好的拟合度。

代理模型精度评价由各模型拟合精度R2和相对均方根误差Erms组成，他们分别为：

式中：k 为样本数量，yk为评估点k 函数的真实值；yˆk为代理模型预测值；yk为函数真实值的平均值；N 为验证样本点的数目。R2越大，Erms越小，则代理模型越精确。通常情况下，R2＞0.9且Erms＜0.2，代理模型精度即可用。

在完成120组基准样本点的计算及变量筛选后，通过优化超拉丁立方算法重新选取50 个样本点进行计算并统计结果，分别构建RSM、RBF、KRG 代理模型，并分析各代理模型精度。

由表5可见，三种类型的代理模型中，KRG模型的R2最接近1，Erms最接近0，整体拟合精度最高。因此，在优化流程中，选择KRG 代理模型。

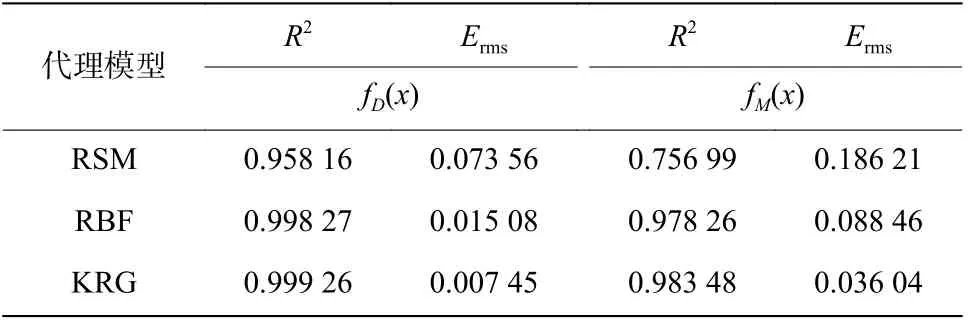
表5 代理模型精度比较Table 5 Accuracy comparisons of different surrogate models

3.4 优化求解分析

根据筛选后的设计变量重新构建数学模型，多目标确定性优化和多目标可靠性优化分别为：

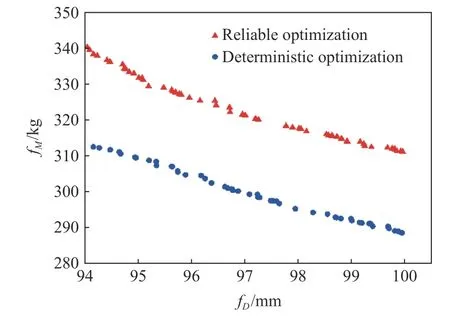
图10 Pareto前沿对比Fig.10 Pareto front comparison

基于KRG 代理模型，运用NSGA-Ⅱ（非劣质分层遗传算法）求解帕累托（Pareto）前沿，设置种群大小为12、遗传代数为200、交叉概率为0.9，所得结果如图10所示。基板最大塑性变形量fD(x)和组件质量fM(x)之间成相互制约关系，即fD(x)随着fM(x)的增加而减少，反之亦然。对比两条散点曲线可见，可靠性优化的Pareto前沿比确定性优化更保守，在相同的基板最大塑性变形量下，可靠性优化设计的组件整体质量均略高于确定性优化的。

对设计目标的取值进行权衡后，在图10中得到最优解。对优化目标fD(x)进行可靠度分析，结果见表6。可见，通过可靠性优化[17]得到的基板最大塑性变形量远离约束边界，设计具有更高的可靠度，但防护组件整体质量略高。

3.5 实验验证对比

根据可靠性优化设计结果，将数据圆整处理后再次进行模拟计算和台架实验，最优设计参数见表7。实验工况与初次实验相同，实验后防护组件整体形变如图11所示。可见，优化后的防护组件在同等级爆炸冲击下未出现破裂，且基板最大塑性变形量明显降低，防护性能得到较大提升。

将所有实验和模拟结果进行对比，具体结果见表8。通过模拟得到优化后的防护组件基板最大塑性变形量fD(x)为97.9 mm，代理模型为99.22 mm，相对误差为1.3%，代理模型准确度较高。实验后测得fD(x)为96.0 mm，与模拟结果相差1.9%，所得结果满足防护要求，组件整体质量fM(x)为320 kg，比初始值低了25.6%。在提高防护组件防护性能的同时，也实现了组件的轻量化，且结果具有更高的可靠度。

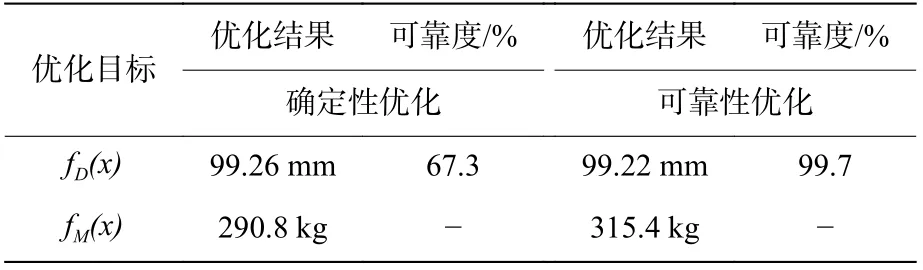
表6 模拟优化结果对比Table 6 Comparison of simulation optimization results

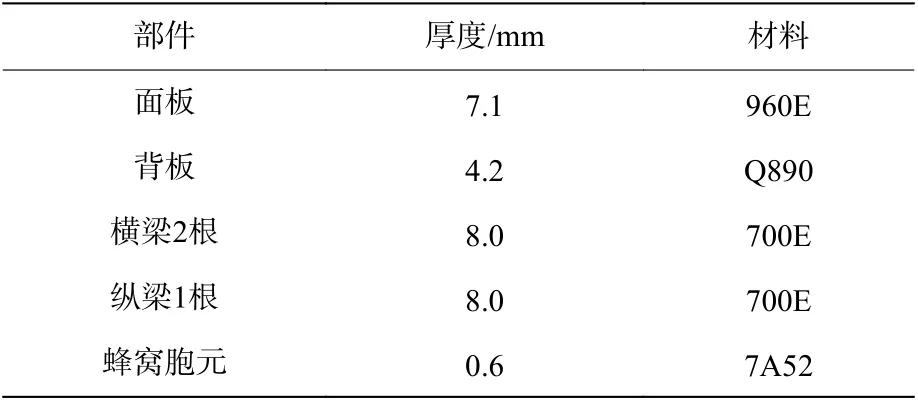
表7 最优设计参数Table 7 Optimal design parameters

图11 优化后基板变形实验结果Fig.11 Experiment result of substrate deformation after optimization

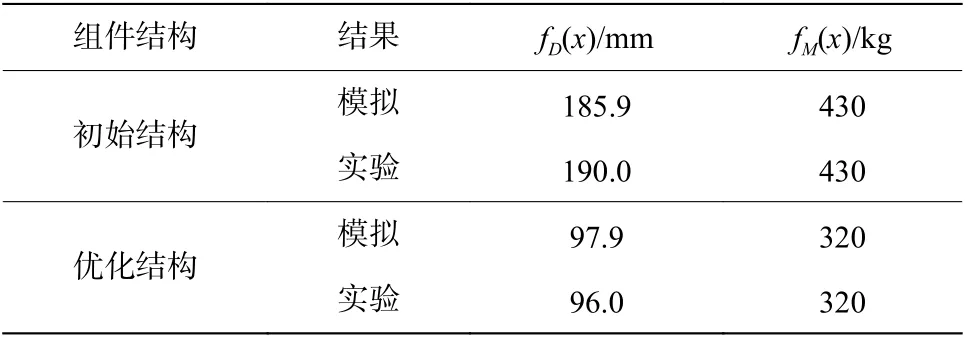
表8 实验与模拟结果比较Table 8 Comparison of experimentand simulation results

4 结 论

设计了一种车辆防护组件的多目标可靠性优化流程，通过数值模拟对比、灵敏度分析、代理模型构建、优化求解，分析确定性优化和可靠性优化，获得了最优的防护组件设计方案，并通过实验验证了优化方案的可行性，在提升防护组件轻量化和防护性能的同时提高了设计可靠性。主要结论如下。

（1）由防护组件所有设计变量对最大塑性变形量和质量响应的灵敏度分析，内部夹层结构中的梁结构对整体设计的影响较小，板件材料和厚度及蜂窝夹层厚度对防护性能影响较大。

（2）比较三种代理模型的拟合精度，发现KRG 模型对本文中的多变量和强非线性工程问题具有更高的应用价值。

（3）可靠性优化相对于确定性优化，所得到的优化结果较保守，但可靠度更高，能为抗冲击防护设计带来更高的安全系数。

对于车辆底部爆炸防护，设计的可靠性要求高于稳健性要求，因此本文中仅做了防护组件的可靠性优化设计。在下一步工作中，如考虑组件的大批量生产应用，可再引入稳健性设计优化。