长杆弹撞击装甲陶瓷界面击溃/侵彻特性*

谈梦婷，张先锋，包 阔，魏海洋，韩国庆

（南京理工大学机械工程学院，江苏 南京210094）

与传统装甲钢相比，陶瓷密度低、硬度高、抗压性能好，在防护装甲设计中有较好的应用前景。高强度陶瓷可以使来袭的高速弹体产生明显的塑性变形，有效防御威胁。射弹撞击陶瓷材料时，弹体材料在弹靶接触面径向流动，靶体无明显的变形行为，这种现象被称为驻留(dwell)。弹体在驻留过程中完全侵蚀的现象被称为界面击溃(interfacedefeat)[1]。

近年来，学者们针对装甲陶瓷界面击溃/驻留效应开展了大量研究工作。Hauver 等[2]率先报道了长杆弹撞击陶瓷复合靶的界面击溃现象。Anderson 等[3-7]、Holmquist 等[8]和Lundberg 等[9-15]对不同速度射弹撞击陶瓷复合靶进行了实验研究。这些实验研究结果表明：在特定的弹靶撞击条件下，陶瓷表面产生驻留或界面击溃现象，后效背板中侵彻深度显著减小；同时，随着撞击速度的提高，弹体在陶瓷表面由界面击溃向侵彻转变。Anderson 等[16]、李继承等[17-18]和Li 等[19-21]在修正流体动力学一维模型(Alekseevskii-Tate(A-T)模型)的基础上，建立了界面击溃条件下弹体变形、动能变化的理论模型。Lundberg 等[9-10,14-15]通过建立运动学方程，获得了界面击溃过程中弹靶表面接触压力，并求得界面击溃/侵彻转变速度表达式，再结合锥裂纹形成与扩展规律，探讨了弹体尺寸效应对界面击溃产生的影响。La Salvia[22-24]分别对陶瓷内微观翼型裂纹扩展与塑性破坏区的产生进行理论描述，分析了界面击溃/侵彻转变过程。Zhang 等[25]和谈梦婷等[26]建立了界面击溃条件下基于翼型裂纹和锥裂纹扩展的陶瓷材料损伤演化模型。学者们对半无限厚的单质陶瓷、有限厚的陶瓷复合靶及陶瓷作为面板的半无限靶的侵彻过程进行了研究。陶瓷与半无限厚金属组成的复合靶(以下简称装甲陶瓷)侵彻理论中较典型的是Fellows等[27]建立的集中质量模型，采用该模型能较合理地对杆形弹高速侵彻半无限陶瓷复合靶过程进行计算，但是模型中弹靶作用耦合机制复杂，参数确定困难，不利于侵彻深度的计算。综上所述，现阶段研究成果局限于分析界面击溃产生的原因及预测界面击溃向侵彻转变的过程，缺乏考虑陶瓷界面击溃/驻留效应的侵彻动力学模型研究工作。通过定量分析界面击溃/驻留效应对长杆弹侵彻陶瓷的影响，可以为陶瓷复合靶结构设计提供有力指导。

长杆弹撞击装甲陶瓷的侵彻深度(depth of penetration，DOP)实验是研究陶瓷界面击溃/侵彻特性的有效手段[28]。本文中围绕长杆弹撞击装甲陶瓷的DOP实验展开研究，分析弹靶撞击过程中的界面击溃与侵彻现象。建立考虑界面击溃/驻留效应的长杆弹侵彻装甲陶瓷计算模型，将模型计算结果与实验获得的不同弹靶条件下的界面击溃/驻留和侵彻特性进行对比，验证理论模型的可靠性。结合理论模型和实验研究对不同撞击速度下弹靶界面击溃/驻留特性和侵彻特性进行规律性分析并研究弹靶材料特性对界面击溃及侵彻特性的影响。

1 考虑界面击溃/驻留效应的长杆弹侵彻装甲陶瓷理论模型

长杆弹以不同速度撞击装甲陶瓷时，随着弹体撞击速度的提高，将出现界面击溃、驻留/侵彻转变过程和侵彻过程。撞击速度较低时，弹体在陶瓷表面径向流动，弹体质量侵蚀、速度下降，陶瓷表面没有明显的侵彻现象，因此后效靶侵彻深度为零，表现为弹体在陶瓷表面界面击溃。随着撞击速度的提高，弹体先在陶瓷表面界面驻留，随后侵彻陶瓷，该过程称之为界面驻留/侵彻转变过程。撞击速度较高时，弹体直接侵彻装甲陶瓷。界面击溃/侵彻转变速度是一定的速度区间，当弹体撞击速度在此区间内时，陶瓷表面将产生界面驻留/侵彻转变过程。界面击溃/侵彻转变速度区间的最小值对应陶瓷出现界面击溃的最高弹体撞击速度，最大值为弹体侵彻陶瓷的最小弹体撞击速度[9]。

考虑界面击溃/驻留的长杆弹侵彻装甲陶瓷模型如图1所示，图1中虚线部分为弹体界面驻留过程。利用该模型可得界面驻留过程中弹靶参数变化规律以及半无限钢靶中的剩余侵彻深度，以分析界面击溃/驻留对陶瓷弹道性能的影响。该模型中主要假设有：

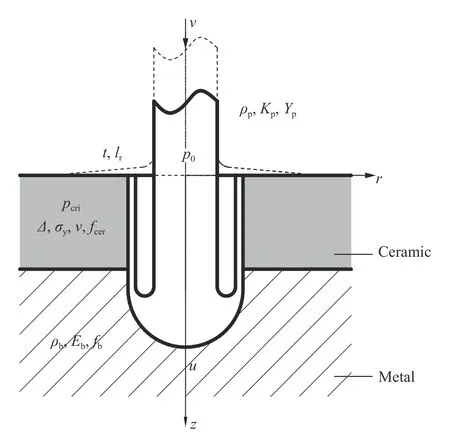
图1 考虑界面击溃/驻留的长杆弹侵彻装甲陶瓷模型Fig.1 A theoretical model of penetration process of ceramic subjected to projectile impact by considering interface defeat/dwell

（1）弹体撞击装甲陶瓷为正侵彻过程；

（2）在界面击溃/驻留和侵彻过程中，弹体头部被视为流体，弹体剩余部分被视为弹塑性材料；

（3）后效钢靶为半无限靶，陶瓷四周没有约束应力；

（4）忽略弹靶间摩擦力。

不同弹体撞击速度下，3种弹靶作用状态对应的计算过程如下：

（1）状态1：界面击溃

根据初始撞击速度，模型在每个时间步都将判断弹靶表面接触压力(p0)小于侵彻陶瓷材料所需压力的临界值(pcri)是否成立。在此基础上计算陶瓷破坏，当弹体完全侵蚀而未能侵彻陶瓷时，弹体在陶瓷表面界面击溃，陶瓷内剩余侵彻深度为零，弹靶作用时间即为界面击溃时间。

Lundberg 等[10]根据弹靶轴线方向的运动方程和von Mises屈服准则获得界面击溃过程中弹靶接触应力为：

式中：u为t 时刻弹体的侵彻速度，u0为弹体的初始侵彻速度，w 为靶体的运动速度。

Li 等[20]分别对弹体侵彻速度衰减u/u0和弹体撞击速度衰减v/v0的一阶近似表达式进行了Taylor 展开，获得了两者比值λ 的近似值：

式中：弹体撞击速度衰减v/v0主要由弹体参数决定，而弹体侵彻速度衰减u/u0由弹靶材料参数共同确定，本文中根据实验结果确定λ 取值为0.82，与文献[20]中λ 取值为[0.81,0.97]相符。

假设界面击溃/驻留过程中陶瓷靶体阻力(fcer)与陶瓷屈服强度(σy)相等，此外，界面击溃过程中弹体侵彻速度为零且陶瓷不运动(w=0)，将式（7）代入式（6），可得界面击溃/驻留过程中陶瓷靶体阻力与撞击速度v 的关系为：

在金属后效靶中的剩余侵彻深度为：

当剩余速度小于侵彻金属靶临界速度时，剩余侵彻深度为零；反之，剩余侵彻深度可由式(14)计算获得。

(3)状态3：侵彻

在较高的撞击速度下，弹靶作用初期即有p0＞pcri。因此，在弹靶作用初始阶段，弹体侵彻陶瓷，该过程可视为状态2的一种特殊过程，其中界面驻留时间为零。计算过程类似，不再赘述。

2 长杆弹撞击装甲陶瓷DOP实验

2.1 弹体与靶体

实验中采用30 mm 次口径脱壳穿甲弹撞击碳化硅（SiC）装甲陶瓷，获得了不同弹体撞击速度作用下金属后效靶中的侵彻深度。弹芯直径为9 mm，长度为90 mm，材料为钨合金，如图2(a)所示。靶体为SiC陶瓷镶嵌于45钢靶中，陶瓷尺寸为100 mm×100 mm×20 mm，内部采用环氧树脂粘接，如图2(b)所示。

图2 弹靶实物照片Fig.2 Photos of projectile and target

2.2 实验方案

实验系统主要由弹体加载发射装置（30 mm 口径滑膛炮）、测速系统、高速数字摄像机组成。利用30 mm口径滑膛炮加载次口径弹体，开展不同尺寸的长杆弹撞击装甲陶瓷实验，实验装置布局如图3所示。通过加载装置将2种弹体加速到700～1 200 m/s飞出，弹体穿透测速靶将信号传递至多通道测速仪，最终撞击装甲陶瓷获得界面击溃或侵彻现象。

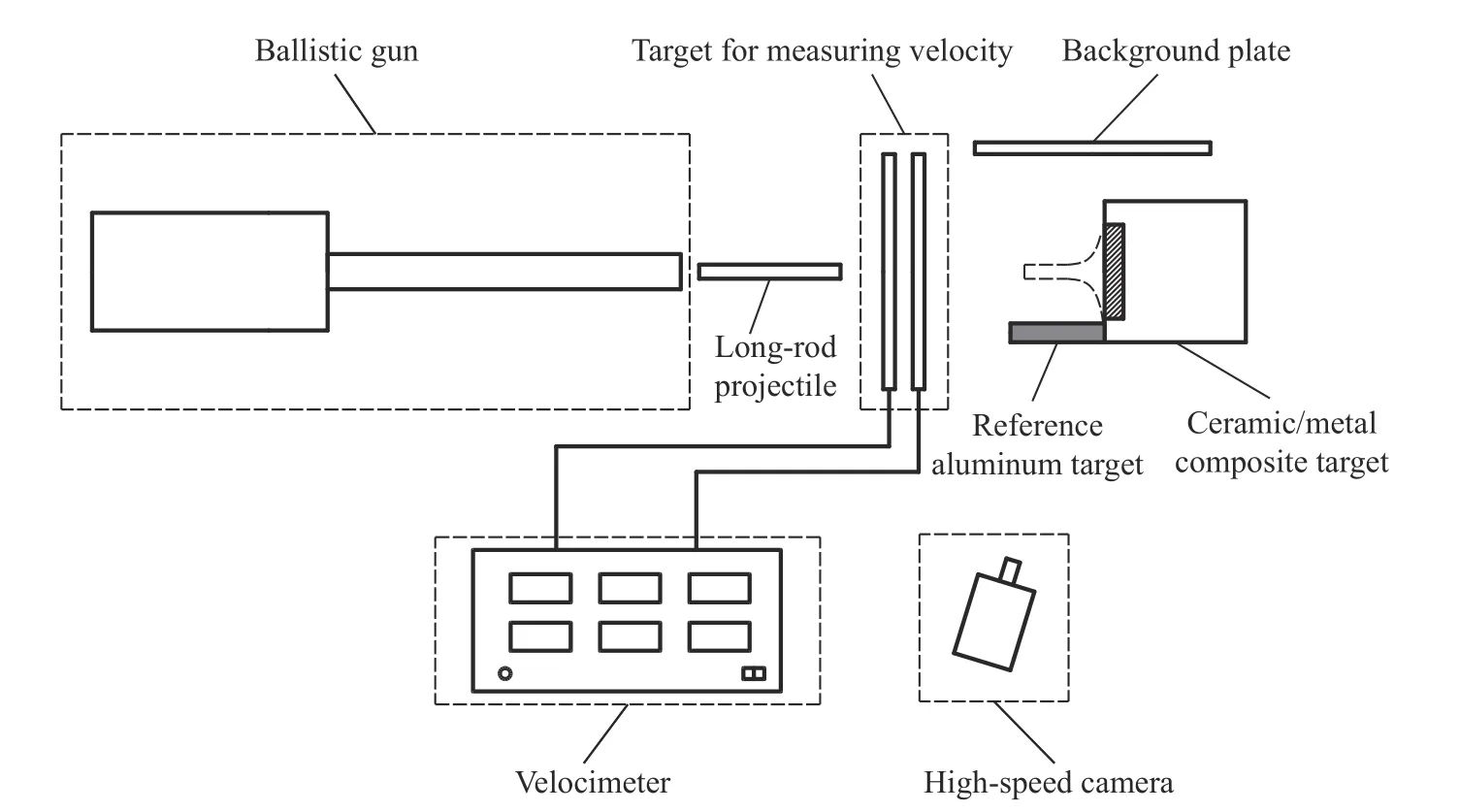
图3 长杆弹撞击装甲陶瓷实验总体布局示意图Fig.3 Experimental layout for the impact of a long-rod projectile into a ceramic armor plate

2.3 实验结果

陶瓷表面的宏观破坏形式是分析装甲陶瓷界面击溃特性的重要参考。图4分别给出了弹体以不同速度撞击装甲陶瓷后陶瓷表面和参照铝靶表面破坏情况。从图4中可以观察到：当弹体撞击速度较低时，陶瓷表面有明显的环向裂纹，无明显轴向裂纹，与Evans等[31]观测的结果类似；当弹体撞击速度较高时，陶瓷表面轴向裂纹与环向裂纹共存，且撞击处存在陶瓷粉碎区；弹体撞击速度越高，粉碎区越小，径向裂纹越多，环向裂纹没有明显的区别。由图4(a)～4(b)可知，在界面击溃过程中，从陶瓷表面观察到的主要破坏形式为环向裂纹、径向裂纹和塑性粉碎区。随着撞击速度的提高，环向裂纹数量变化较小，因此在高速界面击溃过程中，可以首要考虑径向裂纹扩展及塑性粉碎区的形成。实验中在装甲陶瓷下方放置了垂直于靶表面的参照铝靶，如图3所示。从图4(a)～4(b)可明显观察到有破碎材料侵彻铝靶的现象，表明在界面击溃/驻留过程中，弹体材料在陶瓷表面破碎并径向流动，剩余一定速度撞击铝靶。实验中，当弹体直接侵彻靶体时，参照铝靶表面没有破坏现象，表明参照铝靶的破坏可以为界面击溃/驻留现象提供证明。图5为弹体侵彻装甲陶瓷后回收靶体及剖靶情况，从图5可以看出，在高速撞击下，陶瓷层破碎与后效钢靶分离并向外飞溅，仅有小部分陶瓷附着于钢靶表面，弹体在钢靶中留下凹坑。

图4 装甲陶瓷界面被击溃后回收靶体表面的破坏情况Fig.4 Surface damage of recovered armor ceramicsafter interface defeat

图5 锥形头部长杆弹以1 037 m/s 的速度侵彻装甲陶瓷后回收的靶体Fig.5 Recovered target after penetration of a cone-nosed long-rod projectile with the velocity of 1 037 m/s into ceramics

表1中展示了不同撞击速度下弹体侵彻装甲陶瓷后在金属后效靶中产生的剩余侵彻深度。根据界面击溃/侵彻转变速度定义可知，锥形头部长杆弹的界面击溃/侵彻转变速度为980～1 030 m/s，柱形头部长杆弹界面击溃/侵彻转变速度为730～840 m/s。

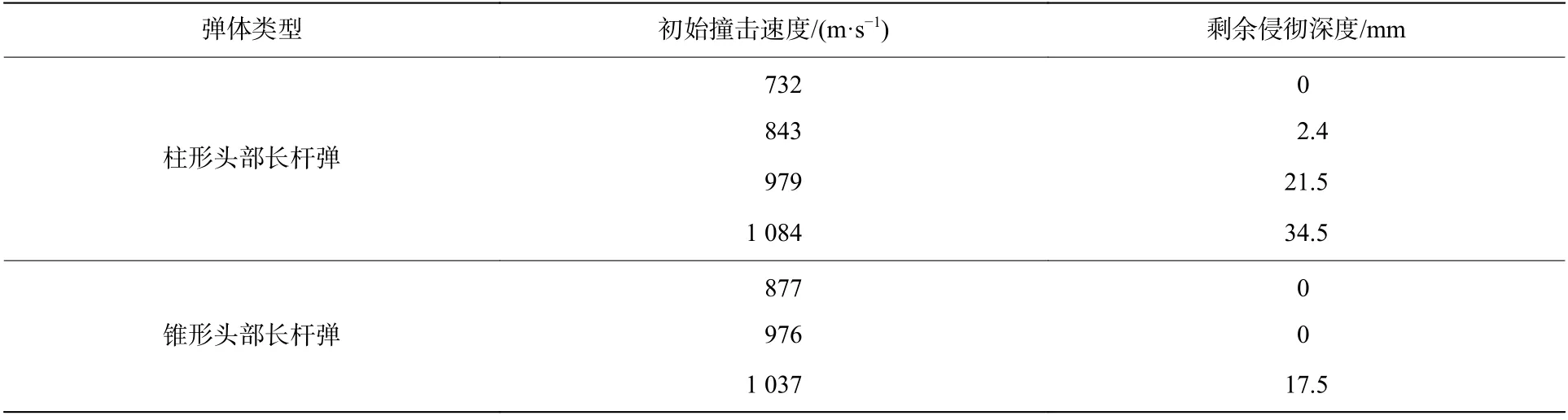
表1 不同撞击速度弹体侵彻陶瓷后金属靶中剩余侵彻深度Table1 Residual depthsof penetration in metal targets after penetration of long-rod projectiles with different velocities into ceramics

3 结果与讨论

3.1 界面击溃及侵彻特性

Behner 等[32-33]开展了与本文类似的长杆弹撞击装甲陶瓷实验，并获得了不同弹靶条件下的侵彻速度、剩余侵彻深度与界面驻留时间。结合弹体和靶体材料参数(见表2～4)，根据Behner 等[32]和本文实验采用的弹体和靶体配置，开展对应实验的界面击溃/侵彻转变速度、侵彻速度、界面驻留时间的理论计算。根据模型计算获得的界面击溃/侵彻转变速度、驻留时间以及侵彻速度与实验结果的对比分别见表5～7，误差均在15%以内，表明理论模型可以合理地预测不同弹靶条件下的界面击溃与侵彻特性。

表2长杆弹相关参数Table 2 Material parametersof long-rod projectiles

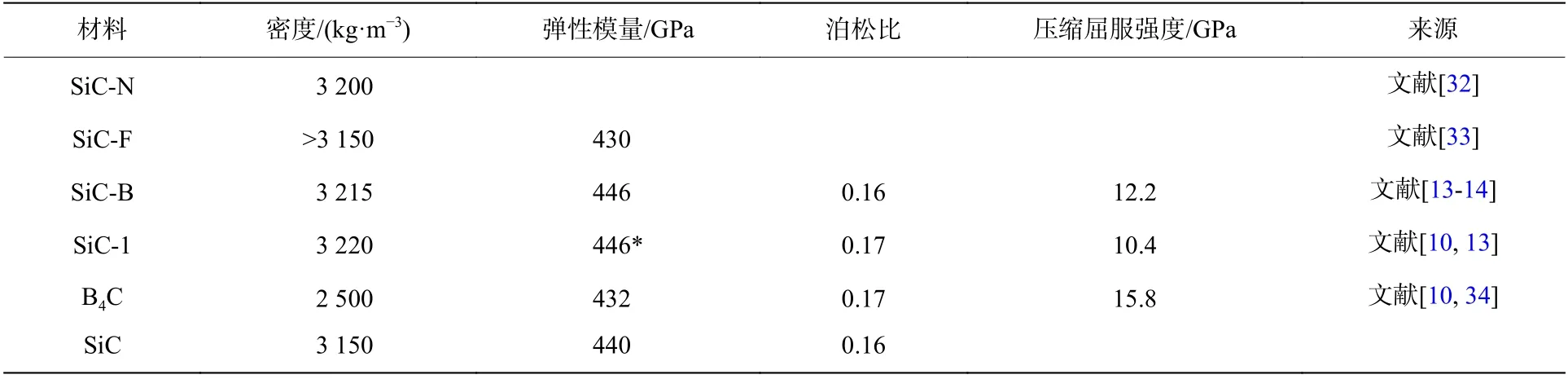
表3 陶瓷相关参数Table3 Material parameters of ceramics

采用第1节中的理论模型对长杆弹侵彻SiC装甲陶瓷进行计算，将获得的侵彻速度和剩余侵彻深度理论结果与本文的实验结果以及Behner 等[33]的实验结果进行对比，如图6所示。图6展示了2次实验中弹体撞击速度由低到高对应的界面击溃、界面驻留/侵彻转变过程及侵彻过程，图中阴影部分为界面驻留/侵彻转变过程。对于Behner 等[33]的实验，当撞击速度低于600 m/s时，陶瓷表面界面击溃，后效钢板中基本无剩余侵彻深度；当撞击速度为600～900 m/s时，弹体在靶体表面驻留，后效钢板中逐渐产生剩余侵彻深度；当撞击速度高于900 m/s时，弹体侵彻装甲陶瓷，剩余侵彻深度与撞击速度呈线性增长的关系。由图6可知，本文实验中侵彻深度随弹体撞击速度的提高而变化的规律与Behner 实验中的相似，均产生侵彻深度无明显变化、非线性变化及线性变化。上述结果表明，本文理论模型计算结果与实验结果一致，计算模型可靠，可进行更深入的界面击溃与侵彻特性分析。

表4 背板材料参数Table 4 Material parameters of back plate

表5 界面击溃/侵彻转变速度的理论计算计算结果与实验结果Table 5 Comparison between calculation and experimental results of transition velocity

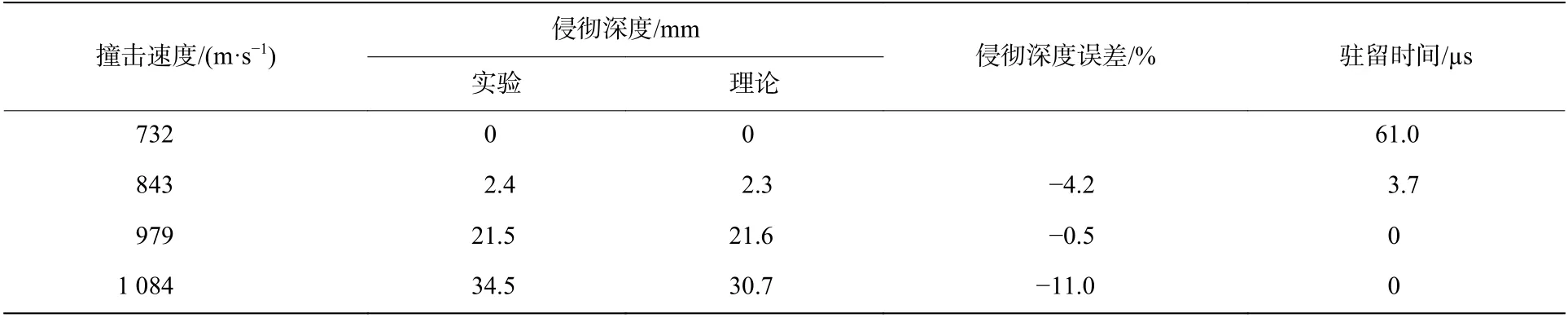
表6 界面击溃驻留时间与侵彻深度与实验对比Table6 Comparison between calculation and experimental results of penetration depth and dwell time

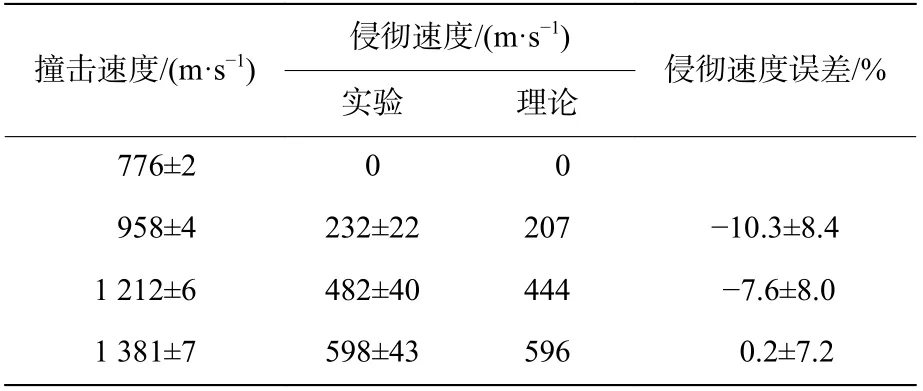
表7 侵彻速度理论值与实验结果[32]对比Table 7 Comparison between calculation and experimental results[32]of penetration velocity

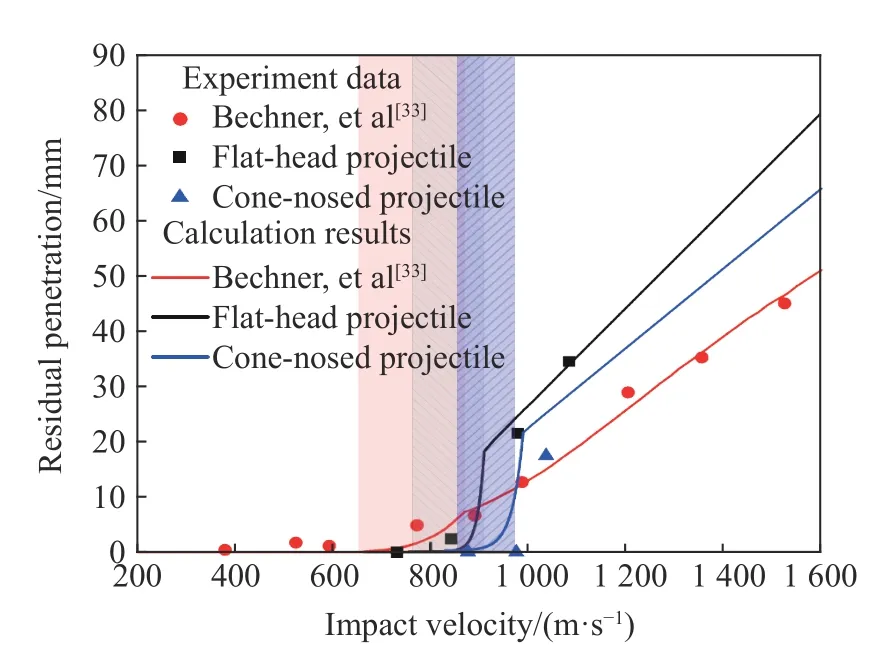
图6 剩余侵彻深度随撞击速度的变化Fig.6 Residual penetration depth varied with impact velocity

3.2 弹体材料对界面击溃/驻留侵彻过程的影响

钨、钼、金材料密度较高，在长杆弹材料中具有较好的应用前景。本文中主要选取钨合金、金和钼长杆弹为研究对象，开展长杆弹侵彻SiC-B装甲陶瓷的理论计算，背板材料采用45钢。相关弹体材料参数和靶体材料参数分别见表2～4。弹体为直径6 mm、质量4.5 g 的圆柱。靶体为陶瓷/钢复合靶，陶瓷置于表面，厚度为25 mm。理论结果计算如图7所示。

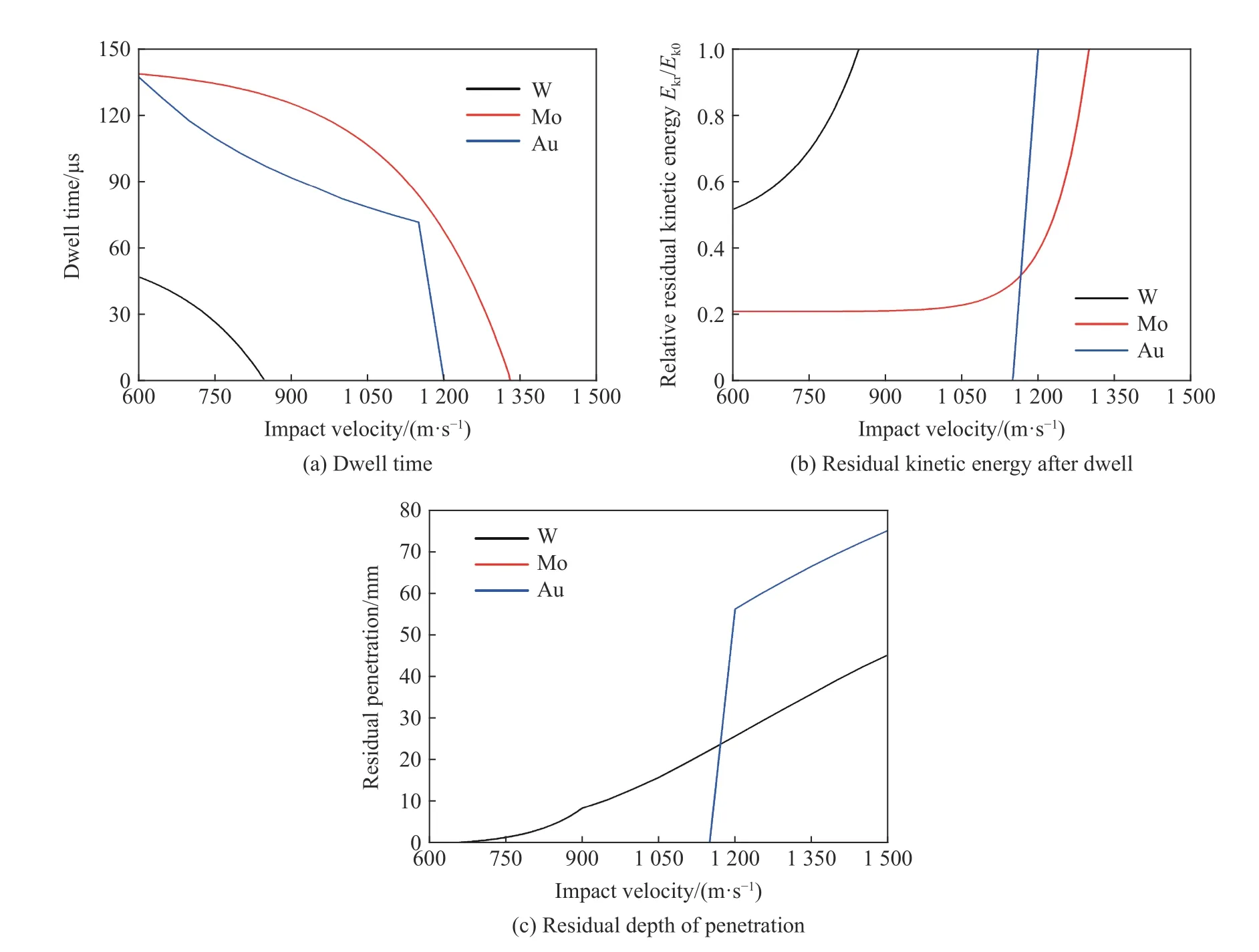
图7 不同材料弹体界面击溃/侵彻过程结果对比Fig.7 Comparison of interface defeat/penetration among projectiles with different materials

由图7可以看出：

（1）图7(a)～7(b)中钨合金与钼长杆弹在界面击溃过程中界面驻留时间与相对动能随撞击速度的变化规律相似，与金长杆弹有显著差异。在较高的撞击速度下，金长杆弹仍出现界面击溃现象。在相同撞击速度下，钼长杆弹产生界面击溃的时间最长，钨合金长杆弹最短，而金长杆弹的动能损失最大。产生这种现象的原因可能是金的压缩屈服强度远小于钨合金和钼，因此在界面击溃过程中，金的质量侵蚀与速度下降快，动能损失较大。

（2）图7(c)中钨合金在较低的速度下在后效靶中产生剩余侵彻深度。钨合金长杆弹在装甲陶瓷中的剩余侵彻深度随撞击速度的变化近似线性；金长杆弹在低速阶段无侵彻深度，当撞击速度高于1 200 m/s时，在靶体中产生较大的剩余侵彻深度；钼长杆弹在600～1 500 m/s 的速度范围内，对装甲陶瓷的剩余侵彻深度最小。撞击速度低于1200 m/s 时，钨合金长杆弹的侵彻性能最优；撞击速度高于1 200 m/s时，金长杆弹的侵彻性能最优。钨合金与金杆弹在不同撞击速度阶段的侵彻性能差异表明，在高速侵彻阶段钨合金的侵彻性能不如金，密度在侵彻深度中起主导作用。

3.3 靶体材料对界面击溃/驻留侵彻过程的影响

选取压缩屈服强度不同的两种SiC陶瓷(SiC-B,SiC-1)和B4C材料作为研究对象，陶瓷材料参数见表3。陶瓷面密度均为80.375 kg/m2，弹体为第3.2节中的钨合金弹体，探讨靶体材料对界面击溃和侵彻性能产生的影响，靶体材料对界面击溃、侵彻的影响结果如图8所示。

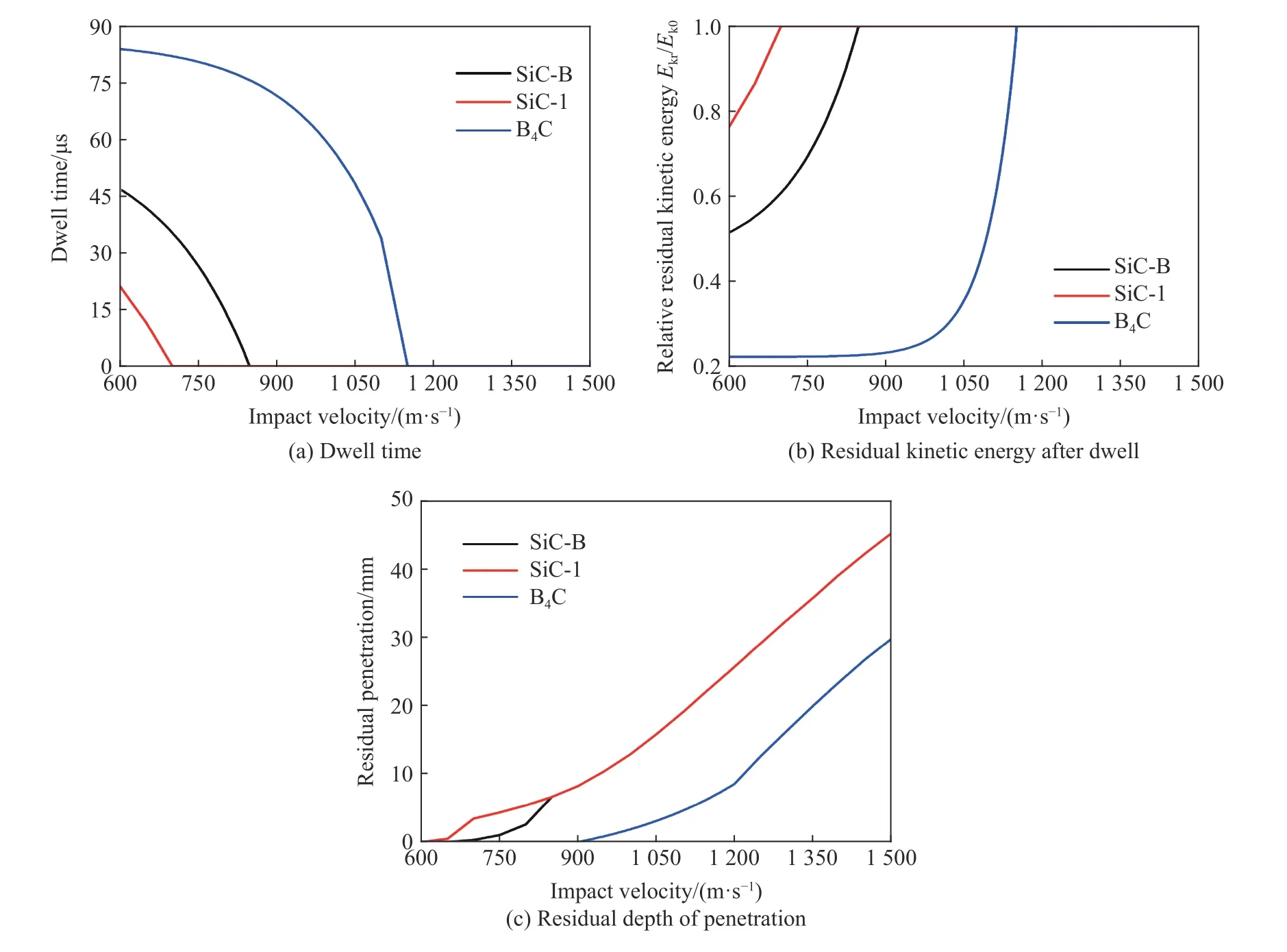
图8 不同陶瓷材料对应的界面击溃、侵彻特性与撞击速度的关系Fig. 8 Comparison of interface defeat/penetration between ceramics with different materials

从图8可以看出：

（1）3种陶瓷材料的的界面击溃特性和侵彻特性类似，其中钨合金长杆弹撞击B4C靶时产生界面击溃的时间最长，损失的动能最多。

（2）长杆弹撞击B4C时，可以在较高速度下产生界面击溃。2种SiC陶瓷在高速阶段几乎无差异；在低速阶段，SiC-B表面更容易产生界面击溃，性能较优。该现象表明陶瓷的界面击溃和侵彻特性与压缩屈服强度密切相关。材料的压缩屈服强度越高，陶瓷材料表面越容易产生界面击溃/驻留效应，弹体消耗的动能越多，陶瓷材料抗侵彻性能越强。

4 结 论

采用30 mm 口径滑膛炮，开展了长杆弹撞击SiC陶瓷实验，采用界面击溃裂纹扩展模型和长杆弹侵彻半无限靶一维模型相结合的方法，建立了基于界面击溃效应的长杆弹侵彻装甲陶瓷的计算模型，结合实验数据与理论计算结果，探讨了陶瓷的界面击溃与侵彻特性，得到的主要结论如下：

（1）通过装甲陶瓷及参照铝靶表面的破坏情况可验证，不同弹体撞击速度下，弹体在陶瓷表面存在界面击溃/驻留过程。

（2）不同弹靶作用条件下的理论计算结果与实验数据吻合，可以较好地预测长杆弹界面驻留时间、界面击溃/侵彻转变速度、侵彻陶瓷速度以及在后效靶中的剩余侵彻深度。

（3）弹体材料性能中，界面击溃效应受弹体压缩屈服强度和密度耦合作用的影响。在高速侵彻陶瓷时，弹体密度越大，其侵彻性能越强。

（4）不同靶体材料的界面驻留特性相似，陶瓷材料的压缩屈服强度越高，越容易产生界面击溃/驻留效应，抗侵彻性能越强。