“学习金字塔”理论在高中数学教学过程中的应用

桑孟娈

[摘  要] 1946年美国学者埃德加·戴尔（Edgar Dale）提出了“学习金字塔”（Cone of Learning）理论，该理论告诉我们：不同的教学方法达到的教学效果不同. 显示了教学情境对教学效果的重要作用. 文章结合一个课堂实录（以“集合间的基本关系”课堂教学为例）详细了解“学习金字塔”的应用，这对教师设置或调整教学方法有导向作用.

[关键词] 学习金字塔;教学方法;应用;导向

[?]前言

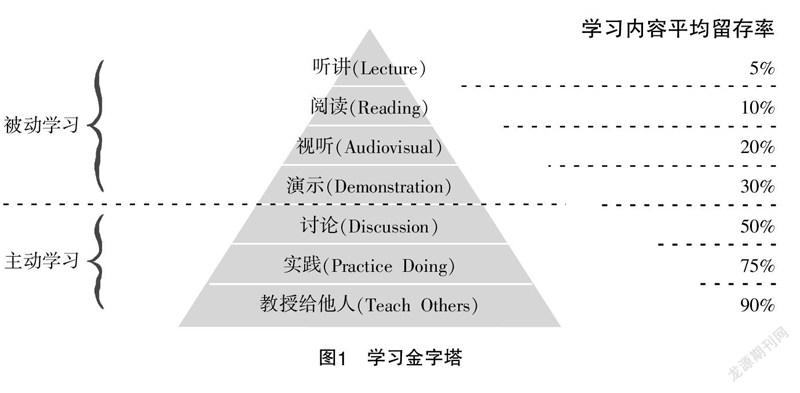
1946年美国学者埃德加·戴尔（Edgar Dale）提出了“学习金字塔”（Cone of Learning）理论（如图1），该理论告诉我们：不同的教学方法达到的教学效果不同. “学习金字塔”理论提出了教学中最常见的7种教学方法，各种教学方法得到的教学效果各不相同. “学习金字塔”塔尖提到的是“听讲”方法，即“教师讲内容，学生听内容”，这是我们最熟悉最常用的一种传统的教学方法，然而其教学效果却是最低的——学习内容留存率只有5%. 其他6种教学方法分别为：“阅读”方法，即“学生用眼睛看学习内容”;“视听”方法，即“学生用眼睛看、用耳朵听学习内容”;“演示”方法，即“教师联动学生利用实验或实物、图表等把学习内容显示出来，供学生认识和理解”;“讨论”方法，即“师生、生生就某一问题交换意见或进行辩论”;“实践”方法，即“在实际应用中学习内容”，也即“在做中学”;“教授给他人”方法，即“学生理解学习内容后教其他同学理解”. 埃德加·戴尔（Edgar Dale）提出，学习内容留存率在30%及以下的几种传统方法，都是个人学习和被动学习，而学习内容留存率在50%及以上的方法，都是团队学习和主动学习.

[?]课堂实录简介

下面，本文结合一次课堂讲解（以“集合间的基本关系”为例）来详细了解“学习金字塔”理论的应用. 说明：在开展“集合间的基本关系”课堂讲解之前，学生已经学过了“集合的概念”.

环节1：教师通过情境类比引入集合之间存在的关系

探究1：在课程开始之时，教师在黑板上列出了一组实数：2____2，3____5， 7____3，1____1+x2，让学生判断这些实数的大小关系.

探究2：当学生轻松完成判断之后，教师请学生类比实数的大小比较，观察下列各组两个集合中元素的特征：①A={1，2，3，4}，B={1，2，3，4};②A={1，2，3，4}，B={1，2，3，4，5}，说一说集合A与集合B有什么样的关系. 由教师通过“男同学”“女同学”和“全班同学”的实际演示引导学生总结：集合A中的元素都是集合B中的元素;集合A中的元素比集合B中的元素少……并由此得出了形象的结论：“A=B，A

探究3：总结完成之后，教师让学生在实际生活中寻找出类似于集合A与集合B关系的两个集合，让学生从自我实践中明白集合之间存在的关系.

环节2：让学生理解集合之间的包含关系

探究4：鼓励学生抽象出集合A包含于集合B的符号表示，选出一些学生抽象的具有特性的符号进行现场展览，与教材中的符号进行对比，并解释教材中符号“?”的来源和用意，由此板书子集的定义.

探究5：引导学生用图形形象地表示出A?B（由学生根据自己的理解画图，表现出了学生的画图兴趣），教师展现了部分学生的图画后板书Venn图.

探究6：请学生再次观察两个集合A={1，2，3，4}，B={1，2，3，4}，并讨论这两个集合的关系，故意引起学生对A?B和A=B的争论. （在争论过程中，可以让学生回忆实数a≤b且a≥b与a=b的关系）

探究7：让认为是A=B的学生用子集的概念向其他学生对两个集合相等作出解释. （教师引导学生逐渐规范描述）

探究8：请学生再次观察两个集合A={1，2，3，4}，B={1，2，3，4，5}，在小组讨论后说出A，B之间的关系. （教师引导学生说出真子集的概念）

研究9：总结子集（A?B）、真子集（A?B）、相等（A=B）之间的关系，鼓励学生从现实生活中举例说明.

环节3：引出空集的概念

探究10：学生解答二元一次方程x2+x+1=0的实数根，从没有实数根引出空集的概念.

探究11：故意引起学生对空集、集合{0}、实数0的争论，在争论过程中回忆集合、元素的概念，更加熟悉、理解相互的区别与联系.

环节4：从集合间的基本关系总结集合的性质

探究12：从问题直接引发学生的讨论和判断：集合的反身性，任何一个集合是它本身的子集（A?A）;集合的传递性，对于集合A，B，C，如果A?B，B?C，那么A?C（由学生用Venn图来表示说明）.

环节5：现场测试

由涉及集合元素、子集、真子集、空集等例题或习题进行测试（例题或习题略）.

在整个“集合间的基本关系”知识的课堂教学中，教师用得最多的教学方法是演示、讨论和实践;由于是新课教学，所以“教授给他人”的时间和机会稍微较小（更适合复习课程时使用）. 在授课的5个环节中，最关键的是“学习金字塔”理论提到的团队学习和主动学习（即学生主体参与度决定着学习内容留存率的多少），这需要激发学生对知识学习的需求和欲望，因此对有效情境的创设把学生学习数学的内部归因激发出来，是实现团队学习和主动学习最大的可能. 在整个课程中，类比情境和画图情境就是关键所在（如表1）——需要明确一点，情境创设需要从学生的已有知识和经验着眼、着手——通过类比情境和画图情境的启发，加上学生多种器官（耳、眼、脑、口、手）的综合使用，对集合之间包含关系和Venn图的认识与理解让整个课程教学的基础得以稳固，使得学习效率有较大的提高.

[?]由“学习金字塔”理论引出有效情境的重要性

從“学习金字塔”理论应用的关键点可以认为，“学习金字塔”理论就是教学主体参与度决定学习内容平均留存率高低的理论. 教学主体参与度与教学效果存在着正比关系. 而教学情境又对教学主体参与度的高低起着关键性作用. 简单递推地说，“学习金字塔”理论提到的学习内容平均留存率体现着教学情境创设的有效性程度，相互存在着正比关系. 因此，创设多维度、多元化的有效教学情境并引入课堂，有意识地引导学生主动参与学习活动，是提高教学效率和教学效果的重要途径.

创设多维度、多元化的有效教学情境并引入课堂，需要对情境素材进行多方面的累积和加工、整合. 教学情境除了让学生在课堂中感觉到数学兴趣，更要让学生感悟到数学学科的学习价值. 为让数学情境能灵活地“融入”数学教学中，使得整个课程教学自然流畅地完成，在数学情境的创设中，教师应掌握以下三个界面.

1. 教学情境的基础性和学科性. 基础性指数学教学情境能让学生了解基本的数学知识，能回忆已学习过的重要的概念、定理、公式等;学科性指数学教学情境需紧扣教学内容，凸显学科重点，能够体现学科知识发现的过程、应用的条件以及学科知识在实际生活中的意义与价值. 情境的基础性和学科性是学生形成学科观念和提高数学素养的基石.

2. 教学情境的逻辑性和层次性. 逻辑性指数学教学情境能引起学生将所学到的概念、定理、公式等用于解决不同的问题，并且在过程中通过整合和加工、归纳和总结学习到新知;层次性指数学教学情境能让学生对重要的概念、定理、公式等进行深层次的了解. 情境的逻辑性和层次性能帮助学生建立知识网络和体系.

3. 教学情境的目标性和高度性. 目标性指数学教学情境能凸显数学知识和技能、解决问题的过程与方法、良好的情感态度和价值观;高度性指数学教学情境能帮助学生完成以上数学教学三维目标，促进学生形成学科观念和提高数学素养.

总之，以“学习金字塔”理论为教学导向，即主导教学以有效情境为基础，将学科、教师、学生结合成有机统一体. 另外，为凸显情境的功能和作用，在创设数学教学情境时，教师需要掌握教学情境的三个界面，对情境素材进行多方面的加工和整合，帮助学生乐于团队学习和主动学习.