基于问题链教学模式的高质课堂
荀峰

[摘 要] 教师在教学中可采用提问的教学方式,让学生在解决问题的过程中培养数学学习能力. 不过,如果教师所提问题与教学内容关联性弱或问题单一,可能会影响课堂效率. 为了使所提问题与所讲授内容更具关联性和方向性,教师可以设计问题链,以提升学生的思维逻辑性、严谨性和敏锐性,从而达到提高知识迁移速度,融会贯通的效果.
[关键词] 学习能力;问题链;知识迁移
教学中教师常常遇到这样的问题:学生上课表现积极,随堂检测做得也很完美,但是过段时间学生就会感觉题目很难,无从下手,出现“一听就懂,一过就忘”的现象. 教学中如何改变这一情况呢?
通过研究,教师发现,采用提问的教学方式可以有效地解决这一问题. 每节课设定明确的教学目标,这样,教学的目的性更容易使学生的思维从模糊到清晰,学习从盲从变为自主建构. 不过,要实现这一目标,靠单一的问题或者无关联问题的罗列显然很难实现,因此所需的问题要具有一定的方向性和结构性,问题链也就应运而生. 下面,笔者结合“方程”知识,具体阐述问题链教学实践,以期和各位同行共同探讨,共同学习.
自主探究
要培养学生分析问题的能力和自主学习能力,教师可以尝试让学生进行自主探究,并选择符合学生学情的问题,让学生通过成功体验增强探究的信心,从而培养其独立思考的能力.
问题1 某超市销售一批书包,平均每天卖出20个,售价为60元/个. 该超市每天书包的销售额为多少元?
分析 销售额=售价×销售数量. 此问题很简单,学生能轻松地给出答案,所以他们参与的积极性很高,课堂气氛活跃.
问题2 某超市销售一批书包,平均每天卖出20个,售价为60元/个,书包的成本为20元/个. 该超市每天卖书包可获利多少元?
分析 利润=(每个书包的售价-每个书包的成本)×销售数量. “问题2”的难度比“问题1”略有提升,但大多数学生都能轻松地解决.
“问题1”和“问题2”相对简单,“问题1”让学生理解了销售额,“问题2”则让学生认识到了销售额和销售利润这两个概念的区别,其能为解决接下来复杂的问题做铺垫. 自主学习不仅能让学生对知识印象深刻,而且能增强学生解决问题的信心.
例题精讲
在新课改的影响下,教师不断尝试改变传统的教学模式,建立以学生为主体的新型课堂,让学生自主地、自愿地参与到课堂教学中. 要实现这一愿望,教师必须充分地利用课堂资源. 例题作为数学教学的重要组成部分之一,是传授知识最直接、最有效的资源,那么在教学中如何更好地应用例题以培养学生主动参与的意识,激发学生的探究热情呢?笔者在例题精讲环节采用了问题链的教学模式,与学生一起探究问题的本质,从而提高了课堂效率.
问题3 某超市销售一批书包,平均每天卖出20个,售价为60元/个,书包的成本为20元/个. 为提升销售额,增加利润,该超市决定降价销售. 假如每个书包的售价每降低1元,该超市每天可以多卖出2个书包. 若该超市希望每天的利润为1200元,每个书包的售价应降低多少元?
分析 题目增加了不确定因素,问题变复杂了,有些学生变得束手无策. 这时,教师带领学生细心分析,一步步突破难关.
师:为解决这个问题,我们是否可以采用方程的思路呢?
生1:可以. 设每个书包的售价降低x元,则该超市每天可以多卖出2x个书包. 根据利润建立等量关系.
师:现在每个书包的售价是多少元?卖出的数量又是多少呢?
生2:现在每个书包的售价为(60-x)元,卖出数量为(20+2x)个.
师:请列出完整的方程,并给出答案.
生3:所列方程为(60-x-20)×(20+2x)=1200,解得x=10或x=20.
师:很好,现在再增加一个条件,使问题变为“超市想尽量减少库存,在盈利不变的情况下,每个书包的售价该降低多少元”,此时该如何解决?答案是多少?
生4:所列方程不变,但解方程后要对方程的解进行取舍. 因为每个书包的售价降低得越多,其销售量就越大,因此最终答案为每个书包的售价应降低20元.
师:很好,看来大家都非常懂销售. 如果这道题再增加一个条件“超市每天会产生50元的额外支出(水、电费等)”,那么,在盈利不变的情况下应如何列方程呢?
生5:只需要在等式左边减去50就可以了,即(60-x-20)×(20+2x)-50=1200.
师:以后大家做生意的时候要记得考虑各种成本,因为去除总成本后得到的才是最终利润. 假如只考虑售价和进价,不考虑人工、房租等成本,最终会造成亏损的.
师:现将原题的“每降低1元”改为“每降低0.5元”,在盈利不变的情况下,该如何求解?(问题给出后,学生有些困惑,这时教师及时引导)
师:变化后,等量关系是否发生改变?
生(齐):没有.
师:设每个书包的售价降低x元,那么x元里面有多少个0.5元呢?
生(齐):个.
师:每降低0.5元就多卖2个书包,那么每降低个0.5元就多賣多少个书包呢?
生(齐):×2个.
自主探究后,学生对销售额和销售利润有了清晰的认识,此时教师带领学生一起学习例题(即“问题3”). 例题变自主探究为师生对话,教师将大问题拆分成若干小问题,在问题的引导下,学生突破了这一难关. 例题精讲后,教师又增加条件,将“每降低1元”变为“每降低0.5元”,制造认知冲突,接着通过问题链为学生解决冲突. 上述过程以问题为线索,提升了师生互动率,课堂气氛活跃了,学生学习的积极性高涨.
拓展提升
为提升学生的创新能力,待学生掌握课内知识后,教师应注意教学内容有所拓展,教学难度有所提升,这样能让学生充分挖掘其智力资源,激起探究热情,同时,起到承上启下的作用——承上是利用已有认知尝试解决问题,以巩固所学;启下是因为拓展题目可能会超出所学知识范畴,通过拓展能激发学生探究新知的热情. 因此,拓展提升对学生的学习大有裨益,应引起教师足够的重视.
问题4 某超市销售一批书包,平均每天卖出20个,售价为60元/个,书包的成本为20元/个. 为提升销售额,增加利润,该超市决定降价销售. 假如每个书包的售价每降低1元,该超市每天可以多卖出2个书包. 要想实现利润最大化,每个书包的售价应降低多少元?
分析 该问题的重点是培养学生对最值概念的理解. 要实现利润最大化,可以直接设出利润为y元,然后根据“问题3”中的等量关系得函数y=(60-x-20)×(20+2x),最后通过函数的最值来解题. 该题的重点不是解方程,而是培养学生的函数思想,让学生解决了一个发展区的问题后自然地进入下一个发展区,层叠递进,从而调动学生学习的积极性,有效地发展学生的思维.
实验检测
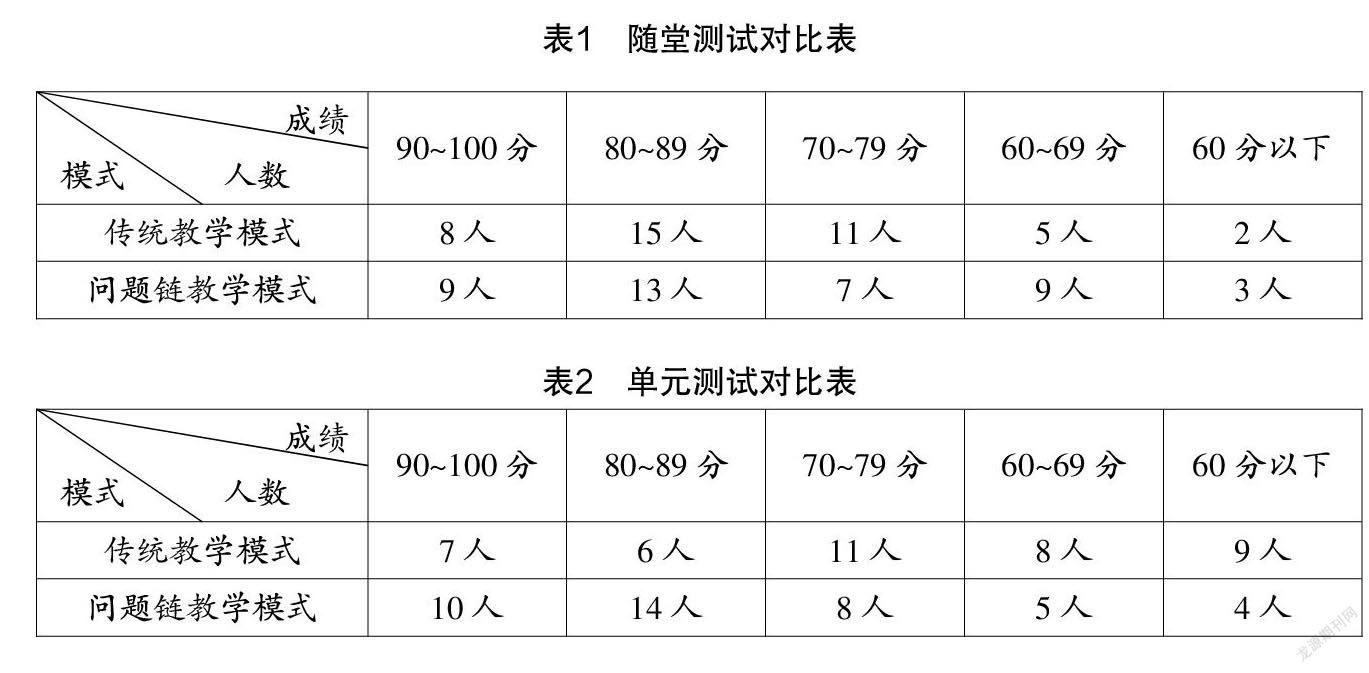
采用问题链教学模式的课堂与传统课堂相比,课堂气氛明显活跃了,参与的人数也变多了,但是仅靠热热闹闹的课堂气氛来检测课堂的生成效果显然不具备说服力. 为了检验课堂效果,笔者采用实验的方式,在两个平行班(人数相同)采用不同的教学模式进行教学,其中一个班采用传统的教学模式,另一个班采用问题链教学模式. 笔者做了两个测试,一个是随堂测试,另一个是单元测试,具体数据如表1和表2.
(1)从“表1”可以看出,用传统教学模式进行教学的成绩更优,因为传统教学模式更倾向于重点的讲解,将注意点及解题思路全部灌输给学生,如果学生会套用就可以取得很好的成绩. 临时记忆在传统教学上表现突出.
(2)从“表2”我们惊喜地发现,用问题链教学模式进行教学的成绩不但没有降低反而提高了,因为问题链教学模式更关注学生分析能力的培养,而分析能力提高后,才能应对千变万化的题目.
从以上两个实验可以看出,采用传统的教学模式进行教学,短时收益较高,但机械记忆必然造成分析能力薄弱,影响思维的灵活度. 数学学习如果依靠死记硬背,不仅时间和精力消耗大,还不利于学生的长久发展. 而采用问题链教学模式进行教学,会使学生对知识的印象更深,记忆更牢,效果更好.
总结反思
在教学中,教师要充分发挥引导者的作用,精心设计问题,引导学生提升知识迁移能力. 同时,问题的设计应采用“低起点,小坡度”的方式,新问题的提出应在原有问题的基础之上,这样既可以让学生够得着,又可以让学生跳一跳,不仅有利于调动学生学习的积极性,提升学生課堂的参与度,而且有利于学生分析能力、推理能力的提升,从而养成独立思考、独自解决问题的好习惯.
总之,以问题为主线引导学生深入学习,有利于吸引学生的注意力,能使学生不会因为时间的流逝而遗忘所学知识,有利于学生知识的积累和学习能力的提升.
3638501908232

