利用GeoGebra软件促进学生的自主探究式学习

王玉洁

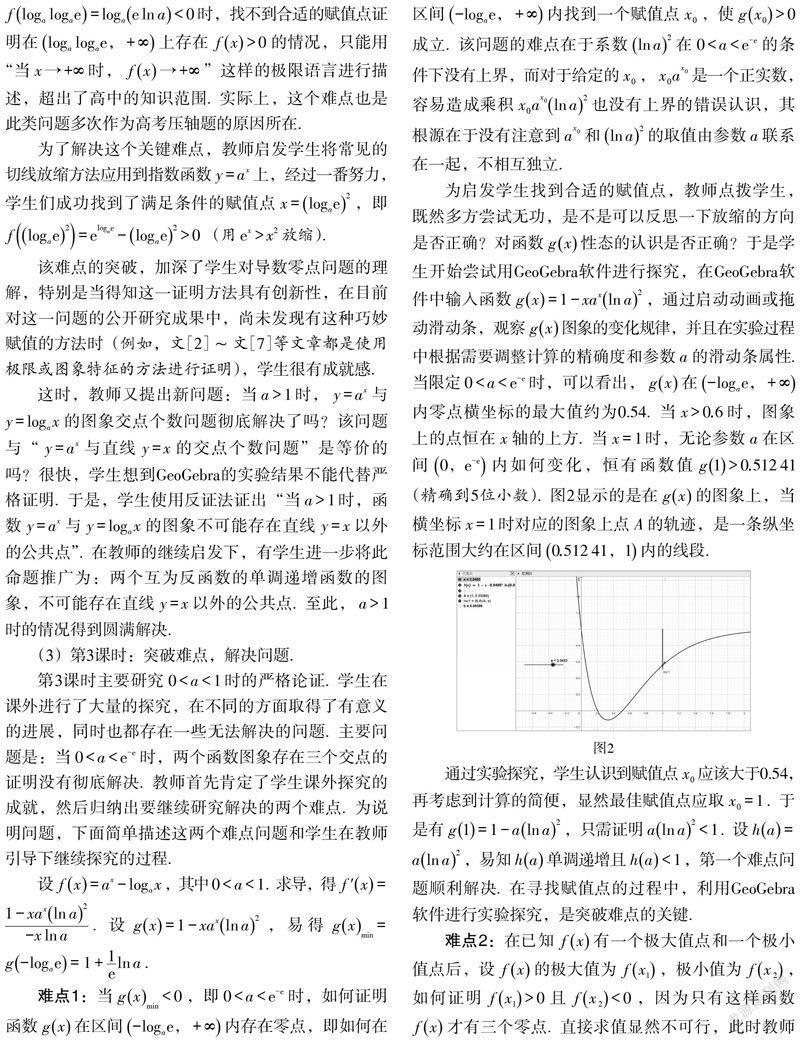
摘  要：以同底数指数函数和对数函数的图象交点个数问题为例，介绍利用GeoGebra软件开展自主探究式学习的具体做法，并给出利用高中数学知识证明这两个函数图象交点个数问题的两个关键环节的赋值方法.

关键词：GeoGebra软件;自主探究;数学实验;图象交点;可视化;赋值

三、结束语

当前，虽然有很多教师在积极探索和推进信息技术与课程教学的深度融合，但是绝大多数教师对这一发展潮流的认识和重视程度还远远不够. 笔者认为，主要有两个方面的原因：一是技术工具的便捷性还有待于大幅度提高;二是技术与教学深度融合的具体路径还不是特别明晰，还需要进行更广泛、更深入的探索.

从高中数学教学来看，GeoGebra软件的便捷性和体验性都很好，但就具体的教学内容而言，怎样才能真正促进深度学习，实现与教学过程的深度融合，需要教师的精细化设计. 以本文所述内容为例，在教师引导学生利用GeoGebra软件探究交点的个数时，自主探究的价值侧重于发现问题;而在[0<a<e-e]的条件下寻找合适的赋值点时，其探究的价值则更多地侧重于解决问题. 无论侧重于发现问题还是解决问题，过程中都有效提升了学生对相关知识内容的本质性认识.

很多教师担心使用信息技术对问题解决的帮助不大，特别是对数学的形式化表达益处不大，如本文中对相应结论的严格证明，还是要跳出信息技术工具的层面用纸笔演算去实现. 首先，在数学教学中，直观是途径和手段，抽象是归宿和目的. 如果在教学中过度依赖可视化方法，会阻碍学生的思维从直观走向抽象，这就要求我们在可视化的认知情境与严格的逻辑推理之间建立适度的平衡. 其次，在数学教学中，应重视让学生经历知识发生、发展的过程，积累数学活动经验，以利于学生逐渐加深对数学的理解，形成并发展数学学科核心素养. 如果学生从一开始就缺乏对数学对象直观属性的认知，很多时候会导致学生无法建构正确的数学概念，出现“盲人摸象”的情况. 而通过信息技术开展数学实验，可以更好地实现学生的自主学习和探究学习，丰富学生的学习体验，能使学生更好地理解数学知识的本质和数学思想方法. 因此，教师在使用信息技术（如GeoGebra软件）开展教学活动时，需要强化信息技术与数学教学融合的工具意识、学习意识、课程意识和发展意识.

参考文献：

[1]祝广文. 介绍一种不超纲的证法：再谈指数函数与对数函数图象的交点个数[J]. 中国数学教育（高中版），2019（10）：62-64.

[2]刘志江. 同底数的指数函数和对数函数图像位置关系探究[J]. 中学数学（高中），2018（5）：76-78.

[3]李惟峰. 对指数函数、对数函数、幂函数交点问题的探究[J]. 中学教研（数学），2008（1）：30-31.

[4]刘志. 指数函数和对数函数的图像交点个数[J]. 高等数学研究，2012，15（5）：43-45.

[5]高明. 指数函数[y=ax]与对数函数[y=logax]的研究[J]. 数学学习与研究，2009（14）：96，99.

[6]高焕江. 指数函数与对数函数图像的两类交点[J]. 红河学院学报，2010，8（2）：36-39.

[7]黃俊明. 关于指数函数与对数函数图像的交点个数问题[J]. 凯里学院学报，2007，25（6）：7-8.

[8]伍春兰，李红云. 基于GeoGebra的数学探究学习的实践与思考：以探究四边形全等条件为例[J]. 数学通报，2018，57（7）：25-28.

3746501908210