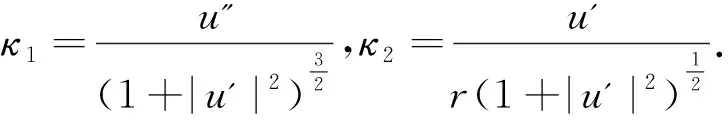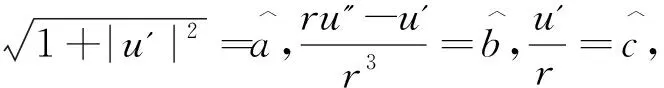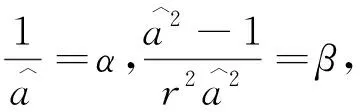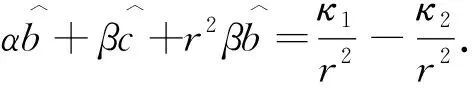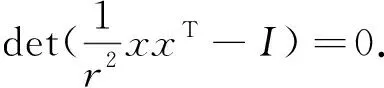一类特殊拉格朗日曲率方程的径向对称解*

梁永梅

(广西师范大学 数学与统计学院,广西 桂林 541006)

1 引言

在二阶椭圆偏微分方程的研究中，边值问题解的存在性问题是最重要问题之一.目前来说，边值问题主要为Dirichlet问题、Neumann问题和斜导数问题，也称第一、第二和第三边值问题.本文研究Dirichlet边值问题解的存在性.众所周知，Dirichlet问题是椭圆方程问题中的一种.而对于完全非线性的椭圆方程，情况是多样且复杂的，特别是微分几何中的拉格朗日方程和拉格朗日曲率势方程.本文把注意力限制在特殊的拉格朗日方程和一些相关的问题上.R. Harvey和H. B. Lawson[1]早在1982年就建立了标量几何理论.根据[1]可设x=(x1，x2，…，xn)，u=u(x)，引入以下方程：

Im(I+iD2u)的像就是拉格朗日方程

arctanD2u=Θ，

其中arctanD2u∶=arctanλ1+arctanλ2+…+arctanλn，λ(D2u)=(λ1，…，λn)是Hessian矩阵D2u的特征值，而Θ称为相.对于这个方程R. Harvey和H. B. Lawson得到了它的解u具有这样的性质:n×n=n中的图p=∇u是绝对体积极小的拉格朗日子流形，并且在任何解处的线性化得到的都是椭圆方程.在早期的工作中，Yuan[2]证明了特殊拉格朗日方程

每一个经典的凸解都必须是一个二次多项式.

近年来有许多文章研究拉格朗日方程[3]，[4]，[5].Collins, Sebastien 和Xuan[4]在2017年研究了一类特殊拉格朗日方程

(1.1)

解的存在性问题，其中Ω是n中边界光滑的有界区域，φ(x)和h(x)是给定的光滑函数.受到文献[4]的启发，本文将其推广到一类具有Dirichlet边值条件的特殊拉格朗日曲率方程

(1.2)

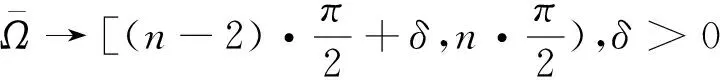
2 预备知识

本节介绍主要的定义、性质以及定理.

在任意区域Ω⊆n上定义一个函数u(x):Ω→，函数u(x)对应的图Γ是n+1的一个超曲面.在嵌入x(x，u(x))所诱导的坐标系中, 欧氏空间n+1在图Γ的诱导度量定义为

gij=δij+DiuDju，

这称为图Γ的第一基本形式.另一方面图τ第二基本形式Γ定义为

(2.1)

取gij对应的逆

(2.2)

结合(2.1)与(2.2)可得

显然地，有

给出σk表示k阶初等对称函数，由下列式子给出

其中λ(A)是实对称矩阵A的特征值.

定义2.1[7]一阶微分方程

(2.3)

这里的f(x，y)是在矩形区域R：|x-x0|≤a，|y-y0|≤b上的连续函数.函数f(x，y)称为在R上关于y满足李普希兹(Lipschitz)条件，如果存在常数L≥0使得不等式

|f(x，y1)-f(x，y2)|≤L|y1-y2|,

对于所有(x，y1)，(x，y2)∈R都成立.L称为李普希兹常数.

定理2.2[7]如果f(x，y)在矩形域R上连续，且关于y满足李普希兹(Lipschitz)条件,则方程(2.3)存在唯一解y=φ(x)，定义于|x-x0|≤h上，连续且满足初值条件

φ(x0)=y0.

定理2.3[8](Schauder定理) 设X是Banach空间，而M⊂X是一个有界凸闭集.如果F:M→M是一个紧算子，则存在x∈M使得F(x)=x成立.

3 径向对称解的存在性

这里给出本文的主要结论.

假设u(r)是方程(1.1)的径向对称解，且u(r)可微.首先，我们从Xiao Ji，Jiguang Bao[6]得到以下结果.

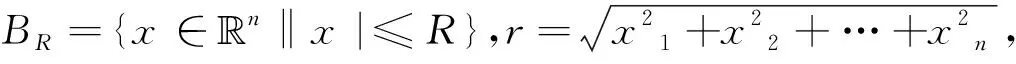
(3.1)

(3.2)

其中λ是Hessian矩阵D2u的特征值.

证明由σk的定义，若(3.1)成立，则(3.2)也成立.众所周知

(3.3)

(3.4)

其中x≠0，1≤i，j≤n.根据(3.3)以及u'(0)=0,知

类似地，利用(3.4)有

因此可以定义

从而有u(|x|)=u(r)∈C2(BR).为证明(3.1)，需定义

由(3.4)可知

D2u(x)=axTx+bI，

其中I是单位矩阵.通过计算可知D2u(x)的特征根是(ar2+b，b，…，b),即(3.1)成立.

观察定理3.1,可以得出类似的结论：

定理3.2对于任意的R>0,令BR={x∈n‖x|≤R},假设u(r)∈C[0，R)， 且u'(0)=0，则对u(|x|)=u(r)，r

(3.5)

证明由σk的定义可知，只需要证明(3.5)成立.

当n=2时

直接计算得

计算相应的特征行列式可得

证毕.

下面利用曲率矩阵A在图Γ∶={(x，u(x))|x∈Ω}的主曲率的表达形式,讨论特殊拉格朗日曲率方程的径向对称解的存在性.

由定理3.2可知方程(1.2)等价于

(3.6)

当n=2时，由(3.6)可得

等价于

令v(r)=u'(r)，则v'(r)=u''(r)，此时(3.6)可写成

定理3.3设微分方程

(3.7)

又由于

从而F是相对紧的，故F是全连续映射，且F(Τ)⊂Τ.于是由一般的Schauder定理可得F在Τ上有不动点，即方程(3.7)有解.证毕.

由于当n≥3时也有类似结论，因此可得到以下定理.