换热管塌料工况识别的试验研究

田俊琪，陈延信，姚艳飞，赵 博

（西安建筑科技大学 材料科学与工程学院，西安 710055）

0 引言

旋风筒被广泛应用于水泥、化工、制药和环保等领域，多用于气固体系或者液固体系的分离。旋风筒由筒体及换热管道构成，粉状物料从换热管进入，在管道内气流对流作用下被分散，完成气体与物料间的逆流换热［1］，之后随气流进入旋风筒筒体进行气固分离。当物料未能良好分散、发生团聚时，部分物料会因无法克服向下惯性力而随换热管塌落至下级旋风筒内，称之为塌料。

徐德龙［2］研究发现塌料的出现会导致气固间的换热效率降低，系统阻力损失增加，进而增加工业生产的系统能耗。李仁龙［3］发现某 2.5×106kg 的新型干法生产线在塌料工况发生时，系统热耗值增加184 kJ/kg。夏祥军［4］指出某1.0×106kg 的新型干法窑因塌料问题导致企业年损失近58.5万元。塌料的出现导致产品质量下降、系统能耗增加，进而导致企业的经济效益下降［5］。因此，塌料工况的发生是实际生产中不容忽视的问题。

目前对换热管塌料工况的研究大多集中在塌料现象及危害等方面［2-5］，对其工况识别及表征的研究相对较少。曾鑫［6］研究了提升管内的压力波动与团聚物特征；杨新等［7］基于颗粒速度计算法建立提升管压降模型，并表明提升管压降可粗略表征提升管物料浓度的分布，为管内气固状态识别提供一定参考；周云龙等［8］利用递归分析研究提升管内颗粒团聚对于系统混沌特征的影响；向杰［9］通过分析提升管内的压力信号，对管内气固流动状态进行了定量表征并表明压力信号的特征量对各种因素的变化更为敏感；杨新［10］通过冷态模拟试验，研究压力信号特征参数与管内物料结块程度、堵塞位置间的关系，并发现压力信号波动特征随故障的不同而呈现不同变化规律；Van 等［11］分析了提升管压力波动的时域、频域分析，发现压力波动的频域分析可对管内气固状态进行描述；姚艳飞等［12］以某生产线为例，采用热工分析对换热管内塌料量进行了计算。

目前，工业生产中通常通过温度及压力信 号［13-14］对设备工作状态进行监控，其中温度通过热电偶等测温装置采集，压力信号通过压力仪表采集。塌料发生时，压力信号会出现瞬时波动，其波动幅度随塌料程度有所不同；温度信号因存在时滞［15］等，基本无变化。基于以上论述，文章选取管内压力信号作为塌料工况识别的关键工艺参数，并构建二维冷态模型，模拟塌料工况，获取不同塌料工况下的压力信号，随后采用功率谱分析和响应面分析法对其进行分析，以期得到一种识别换热管内的塌料工况的办法。

1 试验设计

1.1 试验装置

所搭建二维冷态试验模型如图1 所示，试验装置主要由换热管、旋风筒、螺旋给料机、袋收尘和风机等构成。其中，换热管采用140 mm ×20 mm×4 mm 的有机玻璃管制成。喂料斗内物料 经螺旋给料机进入换热管中，在向上气流作用下，克服向下惯性后随气流进入旋风筒内完成气固分离。分离后的固体粗颗粒沿旋风筒锥部立管进入集料斗，气体则携带较细粉尘经旋风筒顶部排出进入袋收尘进行除尘处理。换热管顶部侧方设置开孔，用于模拟塌料工况。塌料工况下，按设定频率将一定量大颗粒物料从开孔处喂入，大颗粒物料进入换热管内向下运动。因大颗粒物料质量较大，上行的气流无法对其提供足够曳力，大颗粒物料继续向下运动，并从换热管底部排出进入集料斗内，形成塌料。

图1 二维冷态试验模型Fig.1 2D cold-state test model

以换热管入口处为基准，H=90 cm 处记为测点A（见图1（b）），测点处连接压力变送器（量程：-1 000～0 Pa），可实时精确测量换热管中的压力信号。试验过程中，压力信号由LabVIEW 数据采集系统［16］进行采集。

1.2 试验方案

利用所搭建试验平台，分别开展塌料频率以及塌料质量分析试验，采集不同工况下的压力信号用于后续分析。

1.2.1 不同塌料频率的塌料试验

试验设置不同的塌料发生频率，采集不同工况下的压力信号。使用功率谱密度法分析压力信号，获取塌料频率信息。具体方案如下：按表1所示参数开始正常工况试验（物料粒径分布见图2），待系统运行稳定后，称取相同质量的大颗粒物料M2（平均粒径为1.8 mm，颗粒密度为2 300 kg/m3）置于烧杯内，按照频率分别为0.1，0.05，0.03 Hz 将大颗粒物料快速从换热管顶部开孔处倒入，得到不同塌料频率下的压力信号，每组试验重复3 次。

表1 正常工况试验条件Tab.1 Normal experiment conditions

图2 正常工况物料M1 粒径分布Fig.2 Particle size distribution of material M1 under normal working conditions

1.2.2 不同塌料量的塌料试验

将断面风速及单次塌料质量作为控制条件设计试验，采集各工况下换热管压力信号，使用响应面分析方法研究二者与换热管压降的响应关系，再利用其反推计算塌料质量的数学模型。具体方案如下：按表2 所示开展两因素三水平试验，依次称取一定质量的大颗粒物料M2（平均粒径为 1.8 mm，颗粒密度为2 300 kg/m3）置于烧杯内，并快速从换热管顶部开孔处倒入，得到不同风速及不同塌料量下压力信号，每组试验重复3 次。

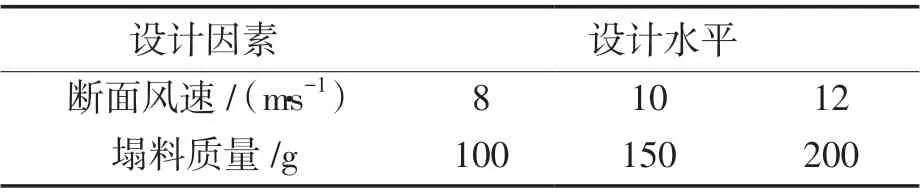
表2 塌料质量试验设计因素及水平Tab.2 Design factors and levels of collapse mass test

1.3 分析方法

1.3.1 功率谱密度法

文章采用功率谱密度法［17］对所获得压力信号进行分析，将压力信号的时间域转化为频率域。时域信号p（t）的傅里叶变换［18-19］定义式为：

功率谱密度函数S（f）定义为：

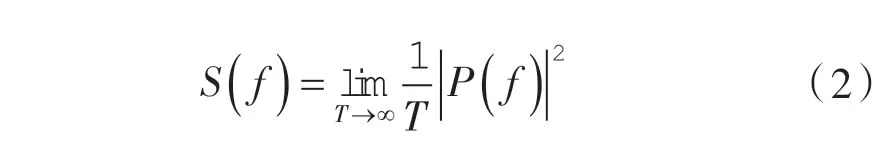
1.3.2 响应面分析法

通过响应面法可以得到响应目标与设计变量间的变化关系，该方法通过对设计空间内的样本点集合进行有限的试验设计，然后拟合出系统响应的全局逼近代替真实的响应面［20-21］。

系统响应与设计变量之间满足函数关系：

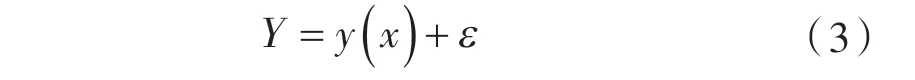
式中 y（x）——确定函数；

ε ——随机误差。

通过试验设计，系统响应与设计变量之间的函数关系可以表示为：

换热管内压降是由管内断面风速与物料质量共同作用，利用响应面分析法对压力信号分析，将断面风速及塌料质量作为输入变量，换热管压降作为输出变量，分析上述两个因素对于换热管压降的影响。在此过程中，可将断面风速与塌料质量的交互作用及二者自身交互作用考虑进来，增加了模型建立的全面性以及可靠性。因此，利用该显著模型进行反推［22-26］即可得到塌料量的数学模型。

2 试验结果

正常工况及换热管存在不同频率塌料时，所采集的压力信号如图3 所示。由图3 可以看出，正常工况及塌料发生时获取的压力信号始终处于动态波动。其原因是物料进入换热管时并非连续均匀，而是成股进入，会导致换热管中的颗粒浓度不稳定，当高浓度颗粒经过测压点时，气流携带颗粒向上运动，颗粒对气流做负功，造成气体压力损耗，该点负压增大，当颗粒离开时，该点负压减小，如此往复，就会造成压力信号的波动。此外，当塌料发生时，压力信号瞬时波动显著，出现明显峰值，且随着塌料频率的变化，峰值出现的间隔时间也随着变化。

图3 正常工况与不同频率塌料工况压力信号对比Fig.3 Comparison of pressure signals under normal working conditions and different frequency collapse working conditions

图4 示出不同风速不同塌料量下所获得压力信号。由图可知，随着塌料量的增加，压力信号波动的峰值也呈增大趋势。表明压力信号与塌料质量存在对应关系，为进一步研究三者之间的联系，下面将对数据进行深入分析。

图4 不同塌料量塌料工况压力信号对比Fig.4 Comparison of pressure signals under the condition of different amount of collapse

3 结果分析与讨论

3.1 塌料工况下塌料频率分析

利用功率谱密度，对图3 中不同频率塌料工况的压力信号进行分析，得到压力信号的功率谱曲线如图5 所示。

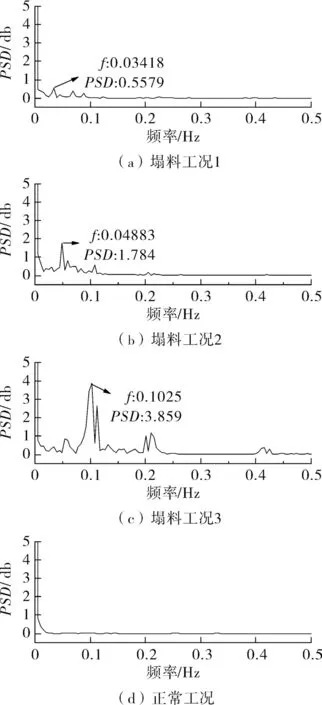
图5 压力信号功率谱曲线Fig.5 Power spectrum curve of pressure signal

由图5 可知，换热管内压力信号的功率谱图在不同频域内的振幅大小不同，其中低频区域谱图振幅较高，高频区域的谱图振幅较小。

观察功率谱曲线，正常工况下，换热管轴向各位置压力信号均没有明显的主频，且波动强度较小。塌料工况1 时，换热管压力信号功率谱曲线中存在f1=0.034 Hz 的主峰，与试验设置频率 0.03 Hz 基本接近；塌料工况2 时，换热管压力信号功率谱曲线中存在主频f2=0.049 Hz 的主峰，与试验设置频率0.05 Hz 吻合；同样地，换热管塌料工况3 时，压力信号功率谱曲线中存在主频f3=0.102 Hz 的主峰，与试验设置频率0.1 Hz 吻合。通过对压力信号的功率谱分析，可以对塌料工况进行鉴定，并对塌料频率进行表征。

3.2 塌料工况下塌料质量表征

塌料发生时，气体对塌落物料做功，产生额外能量损耗fw，则此时，换热管道正常工况与塌料工况的压差为：

图6 示出ΔP 随断面风速及塌料质量变化的影响规律。同一断面风速下，塌料质量越大，气体对塌落物料做功越多，ΔP 越大。同一塌料质量，风速越大，换热管内粉尘浓度越小，气体对塌落物料做功越少，ΔP 越小。

图6 不同断面风速及塌料质量工况下的ΔPFig.6 ΔP under different cross-section wind speed and collapse mass conditions

依据试验所得数据，以管内压降为响应变量，以断面风速v 和塌料质量m 为输入变量，通过响应面分析方法的多项回归拟合得到二次回归模型，如下式所示：图7 示出通过响应面分析得到的断面风速与塌料质量对换热管压降的响应关系，并对模型本身及模型项进行了显著性分析，结果见表3。

图7 断面风速与物料质量对换热管压降的响应关系Fig.7 Response relationship between cross-section wind speed and material mass to pressure drop of heat exchange tube

表3 响应面回归模型ANOVA 分析结果Tab.3 ANOVA analysis results of response surface regression model

模 型F=413.15、P＜0.000 1，证 明 该 回 归模型对试验结果影响显著［27］；模型回归系数R2=0.978 2，相关调整系数RAdj2=0.975 8，R2与RAdj2均接近1，表明该模型的预测压降与试验数据吻合程度高；方差分析结果中变异系数CV=6.57%，小于10%，表明模型预测值具有很好的可信度和精密度［28］。综上所述，该模型对管内压降的拟合程度较好，因此可以使用此模型来分析和预测在不同条件下风速与塌料量对管内压降的影响。

因此，对式（8）进行反推可得塌料质量关于断面风速和管内压降ΔP 的函数模型：

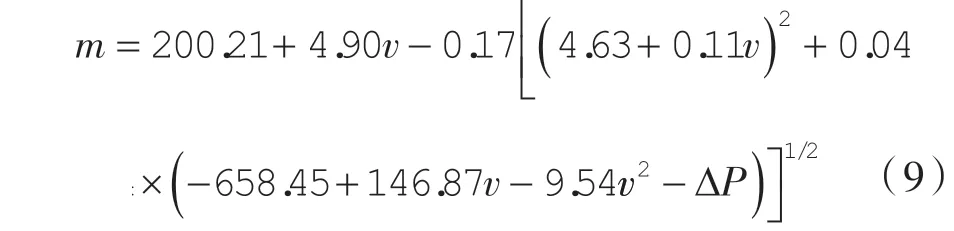
将试验数据代入该函数模型进行验证，结果如图8 所示。

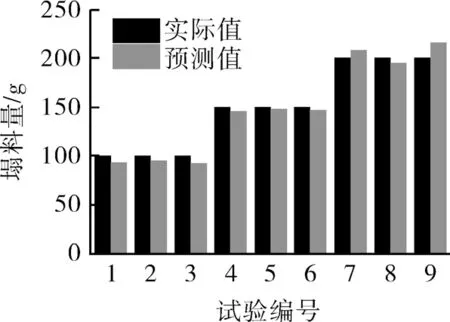
图8 塌料量模型预测值与实际值对比Fig.8 Comparison between actual value and predicted value of the model

将图中塌落物料质量实际值与模型预测值进行对比，两者差别很小，其平均相对误差为3.79%，证明该模型具有较好的可信度，能较准确地估计出管内塌落物料质量。因此可使用此模型在已知断面风速与管内压降时，分析和预测不同塌料工况下的塌料质量。该模型的构建，为实际生产中换热管塌料质量的预估提供了一定指导 作用。

4 结论

（1）塌料发生时，压力信号瞬时波动显著，出现明显峰值，塌料工况对压力信号作用明显。

（2）通过对压力信号的功率谱分析成功检测出换热管在不同塌料频次下存在塌料频率分别为0.102，0.048，0.034 Hz 的塌料信号，与试验设置频率基本吻合。此方法成功辨识出塌料工况并表征了塌料的频次。

（3）依据能量守恒定律，结合响应面分析软件分析构建了压降关于塌料量以及断面风速的数学模型，通过方差分析CV=6.57%，证明该模型显著，可信度高，将模型反推得到塌料量关于压降以及断面风速的函数模型，并通过数据验证该模型预测值与实际值平均相对误差为3.79%，证明了该模型的可行性。

综上所述，压力信号对于塌料工况的瞬时反应明显，并通过对压力信号的分析，可以实现对塌料工况的鉴定以及塌料频率与塌料质量的表征。