对转轴流泵的设计与数值分析
李靖晗,胡永海,阮鹏程,朱 兵
(1.上海理工大学 能源与动力工程学院,上海 200093;2.上海市动力工程多相流动与传热重点实验室,上海 200093;3.中国电建集团 上海能源装备有限公司,上海 201316)
0 引言
对转叶轮由2 个叶轮串联在一起,以相反的方向绕同一轴心旋转,其具有结构紧凑、单位体积/重量做功能力强、叶尖速度低和减振降噪等特点。
目前在多个旋转机械领域,对转式叶轮已经得到了应用和研究。许剑[1]针对一对转风机,采用模拟平面叶栅的计算方法,考察了前、后转子载荷分配规律,并给出了合适的范围,提高了风机的压比。聂延生等[2]设计了对转螺旋桨,分析印证了对转结构叶轮可提高推进效率和系统运行稳定性。史磊等[3]以一双排对转轴流压气机为研究对象,通过区域缩放法开展非定常数值研究,发现在转子轮缘端壁处设置抽吸孔,低能流体的移除能够明显改善叶尖区域的流场品质,提高压气机工作特性。赵红玲等[4]以逆向双转子高效发电装置为基础,设计研究了一种逆向双转子风力发电机,有效降低了电能转换成本。
针对水泵领域采用对转结构叶轮,国内外学者也开展了一些研究工作,初步证明了这种新型结构叶轮的技术优势及在喷水推进领域的应用前景。Akinori 等[5]针对对转轴流泵展开了研究,提出了对转轴流泵的比转速概念;发现对转轴流泵具有扬程高、结构紧凑和泵体较轻等特点,后置叶轮对提高泵整体效率十分重要;考察了叶片数、叶栅稠密度、叶片安装角和叶型等对整个泵性能的影响。Shigemitsu 等[6]通过试验手段对比了对转轴流泵与普通轴流泵的空化特性,发现对转轴流泵叶轮的抗空化性能更好,稳定运行区更宽,但其外特性曲线在小流量工况区会出现正斜率现象。王德军等[7-9]也对对转轴流泵进行了设计和数值分析工作,提出了在原始设计参数中适当提高次级叶轮设计扬程的方法,可使其水力性能得到进一步提升。近年来,一些学者对采用对转叶轮的轴流泵在喷水推进领域的空化特性进行了数值分析工作,证明采用对转叶轮可以提高轴流泵的抗空化特性[10-14]。
虽然对转轴流泵具有较好的特点和应用前景,但目前对对转轴流泵的研究较少,也没有形成成熟的设计方法和理论。本文旨在探索基于仿真驱动的对转轴流泵的参数化设计方法,并采用数值的方法探索一些前、后叶轮匹配参数对泵性能的影响。
1 对转轴流泵的设计
1.1 设计流程和方法
为简化对转轴流泵的设计流程,利用Matlab软件构建一个对转轴流泵参数化设计平台。在此平台中,程序可根据设计要求自动对重要设计参数进行调整,直至得到满足指标要求的对转轴流泵模型,具体流程如图1 所示。

图1 对转轴流泵设计流程Fig.1 Design process of counter-rotating axial flow pump
首先,根据传统轴流泵设计方法,汇总所有相关水力计算公式,利用Matlab 软件实现计算过程自动化。当输入设计参数,程序自动采用默认参数完成初始水力计算,对涉及的经验系数可在建议范围内供使用者进行重新调整。程序后台内置建立一个翼型数据库,以供选择所需合适翼型,并将其转换为三维柱面坐标系数据,输出可供叶轮网格划分软件TurboGrid 读入的几何文件(hub、shroud、profile)。借助Matlab 平台,将后续Turbogrid 网格划分、调用CFX 求解和性能结果统计进行数据连接,优化调整关键设计参数,最终实现对转轴流泵的参数化设计。
1.2 叶轮叶片的选型与绘型
根据升力法和水力计算结果,从翼型数据库中选择翼型,本文选NACA4412 翼型。程序则自动读入平面翼型的上、下表面坐标,并对读入坐标进行拟合,得到函数y1=f(x)和y2=g(x)。记上行线与内切圆相切点的坐标为[x,f(x)],下行线与内切圆相切点的坐标为[ ,y()],y()也为g(x)的值,O 为左端圆弧圆心,P,Q 分别为切点,如图2 所示。
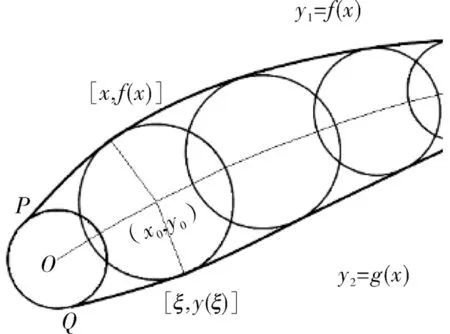
图2 翼型中弧线坐标关系Fig.2 Coordinate relationship of arc in the airfoil
翼型中弧线坐标可由关系式(1)解出。在此基础上,对获得的中弧线进行函数拟合,并根据从轮毂到轮缘的线性加厚规律对翼型进行加厚。
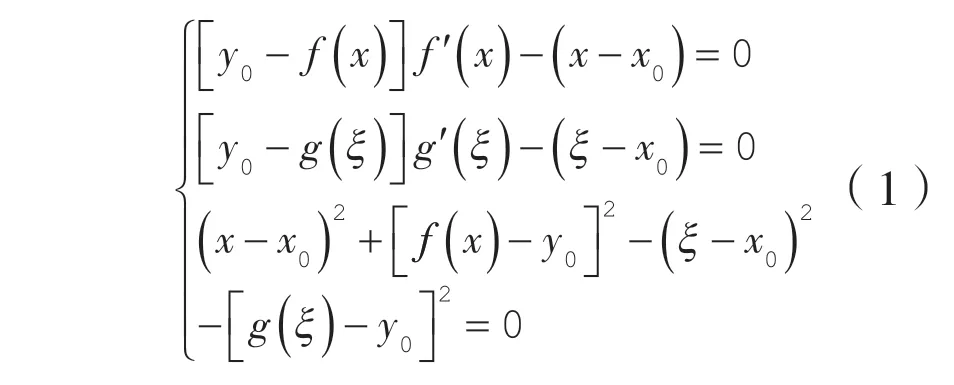
叶轮空间叶片的绘制则根据水力设计计算值来选取缩放比例和安放角度,通过对不同圆柱面上的翼型坐标进行缩放、平移、旋转变换和平面向柱面投影操作来实现。
1.3 数值计算方法
本文确定的对转轴流泵模型设计参数为流量70 L/s,前、后置叶轮扬程均为2 m,设计转速 1 225 r/min,前置叶轮叶片数为4,后置叶轮叶片数为5,叶轮直径200 mm,轮毂直径100 mm,具体设计参数见表1。设计好的前、后置叶轮几何文件直接导入叶轮网格专用划分工具Turbogrid,采用其内置的宏进行结构化网格自动划分。为了减少计算规模,分别选取两个叶轮的单通道组合进行模拟。根据以往网格相关性的测试经验[15],在设计点附近,单个叶轮通道网格数量控制在50万左右,这对流场分析和性能计算的影响就可以控制在一定的精度范围内。采用ANSYS CFX 通用软件包进行稳态数值模拟、泵的性能预测和流场分析。该软件将压力场和速度场进行耦合求解,保证了复杂流场计算的稳定性和快速收敛性。计算域的进口采用总压、出口采用质量流量边界条件。叶轮转子壁面边界定义为旋转边界,其余壁面采用为无滑移边界。两叶轮之间采用多参考下交界面模型进行数据插值和信息交换。鉴于剪切应力输运模型SST(Shear Shress Transport)兼具k-ε和k-ω模型的优点,目前已经在各行业里得到成功应用,本文也选用SST 湍流模型。稳定控制方程对流项采用混合二阶精度离散格式,其它项均采用默认二阶中心差分格式。方程的迭代收敛除了通过监控均平方根残差外(默认10-4),还通过监控关心的扬程和效率随迭代过程的变化过程来综合判断计算结果的收敛性。

表1 水力设计主要参数Tab.1 Main parameters of hydraulic design
2 设计参数匹配分析
2.1 前、后置叶轮载荷分配的影响
在前、后置叶轮均分扬程(各为2 m)载荷的设计条件下,数值计算获得泵的总扬程为3.77 m,总水力效率为76.7%;且发现前置叶轮的效率和扬程明显高于后置叶轮。这与日本学者采用相同设计参数条件下的实验测试结果较为接近[5](扬程3.7 m,效率在70%)。由此可见,目前的设计过程和方法是可行的,但针对一些设计参数还需要进一步优化。
结合文献[16]的载荷优化思路,在已有设计方案的基础上,通过微调前、后叶轮转速的方法对前、后置叶轮的载荷进行重新分配,并用数值计算分析其影响,结果见表2。

表2 前、后置叶轮载荷分配Tab.2 Load distribution on front and rear impeller
可见,后置叶轮的效率和扬程基本上小于前置叶轮。通过重新调整前、后叶轮转速来重新分配载荷,发现后置叶轮转速的降低虽然减小了扬程输出,但提高泵总体运行效率。
2.2 轴向间隙的影响
为了分析前、后置叶轮轴向间隙的影响,取间隙值与前置叶轮弦长比例I 分别为0.01,0.05,0.06,0.08,0.12 及0.24,进行数值计算。图3 示出了前、后置叶轮轴向间隙对泵性能的影响。

图3 轴向间隙与扬程、效率的关系Fig.3 The relationship between axial clearance and head and efficiency
结果表明,当轴向间隙为前置叶轮弦长的5%左右时,泵的扬程和效率均达到最优;当轴向间隙较小时,泵的性能变化较小;而当轴向间隙较大时,前置叶轮出口处的动能损失增加,使得泵性能急剧下降。
分别取轴向间隙比I 为0.01,0.05,0.12 的计算结果,图4,5 分别示出后置叶轮不同截面位置上的速度分布和压力分布。由速度分布图可见,随着轴向间隙的增大,前置叶轮对后置叶轮的影响、以及从叶根到叶梢的影响均逐步减弱;由后置叶轮叶片各个径向位置截线上的压力分布对比可见,随着轴向间隙的增大,叶片两侧压差大小减小,叶轮做功能力明显下降。

图4 后置叶轮叶片不同截面位置速度分布Fig.4 The velocity distribution at different cross-sectional positions of the rear impeller blades

图5 后置叶轮叶片不同截面位置压力分布Fig.5 Pressure distribution at different cross-sectional positions of the rear impeller blades
2.3 后置叶轮转速的影响
固定其它设计参数不变,仅调整后置叶轮转速,以分析其对泵整体性能的影响,获得的性能曲线随流量的变化如图6 所示。针对设计转速工况,当泵的流量为10~50 L/s 时,扬程曲线较为平坦,当流量大于50 L/s 后,扬程逐渐下降;泵的最高效率点在设计流量70 L/s 附近;与传统导叶式轴流泵相比,对转轴流泵的运行高效区相对较宽,且在小流量工况没有发现扬程曲线的“驼峰”现象。
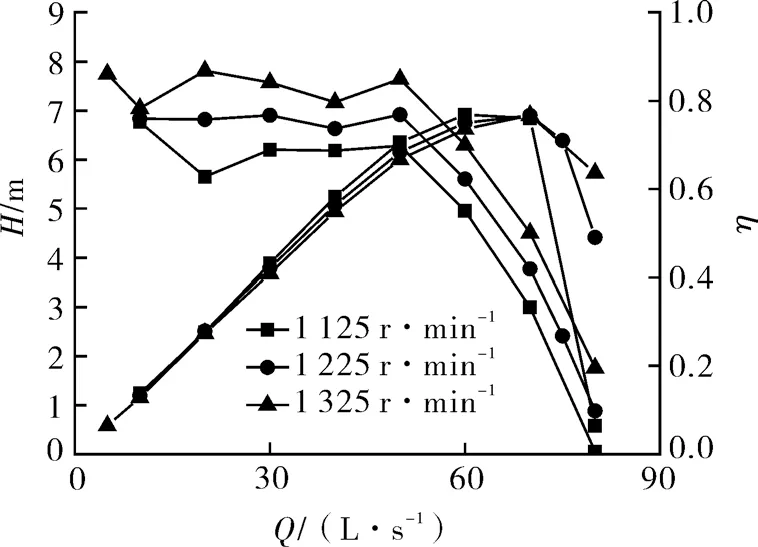
图6 后置转速变化对轴流泵性能的影响Fig.6 The influence of the rear speed change on the performance of axial flow pump
当调整后置叶轮转速后,发现泵效率基本不变;而扬程随后置叶轮转速的增大而增大。随着后置叶轮转速的增大或减小,扬程曲线在小流量区出现波动,由此推测后置叶轮与前置叶轮的转速不匹配可能是轴流泵扬程曲线出现“驼峰”现象的主要原因。
在流量为20 L/s 时,选取后置叶轮转速分别为1 225 r/min 和1 125 r/min 的计算结果进行对比分析。图7,8 分别示出了后置叶轮径向截面上的速度和湍动能分布。

图7 后置叶轮径向截面的速度分布(Span=0.5)Fig.7 The velocity distribution on the radial section of the rear impeller(Span=0.5)
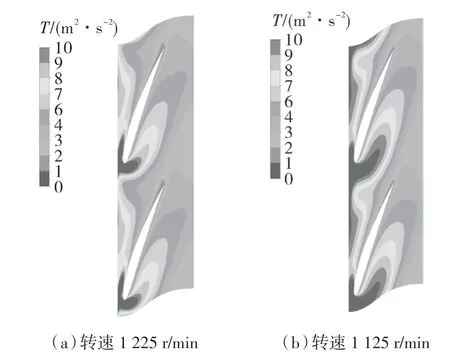
图8 后置叶轮径向截面的湍动能分布(Span=0.5)Fig.8 The turbulent kinetic energy distribution on the radial section of the rear impeller(Span=0.5)
可见,当偏离设计工况时,后置叶轮发生了大的分离,分离区湍动能也明显增强,从而使得扬程曲线在此流量下出现 “驼峰”下降现象。这证明了可以通过调整后置叶轮的转速使其与前置叶轮匹配,以削弱或者消除“驼峰”现象,从而拓宽运行工况范围。
3 结论
(1)应用Matlab 软件实现了对转轴流泵的参数化设计,并搭建了分析优化设计平台,将设计分析结果与参照试验结果对比,表明本文提出的对转轴流泵的设计流程和方法是可行有效的。
(2)后置叶轮的效率及实际扬程一般要低于前置叶轮,可以通过重新分配载荷,降低后置叶轮的转速来提高整体效率;轴向间隙存在最优值,建议设定为前置叶轮弦长的5%左右。
(3)后置叶轮转速的合理选择能够减弱或消除轴流泵在小流量工况扬程曲线出现的“驼峰”现象,从而拓宽了轴流泵运行工况范围。

