基于混沌加密的快递隐私信息保护*

陈 云，周大伟，李 强，王家俊

（海军工程大学，湖北 武汉 430033）

0 引言

近年来，我国电子商务的快速发展带动了快递行业的迅猛发展，使其成为我国经济的一匹黑马。快递服务已成为人们日常生活中不可或缺的一种服务方式。据国家邮政局统计，2018 年我国快递行业发展迅速，全年业务收入达到6 038.4 亿元，同比增长21.8%。全年快递业务量达到507.1 亿件，同比增长26.6%，超过美、日、欧发达经济体之和，规模稳居世界第一，占全球快递包裹市场的一半以上，已成为全球快递市场发展的动力源和稳定器[1-2]。

我国快递行业迅猛发展的同时，快递实名制已于2015 年11 月1 日在全国范围内推开，快递信息安全成为快递行业中面临的重要问题，突出表现在以下3 个方面：

一是快递面单上的用户隐私信息保护问题。快递面单上包含了未经任何加密处理的姓名、地址、电话号码等发件人和收件人详细信息，容易造成个人隐私信息的泄露。仅2015 年，有统计的全国快递企业重大信息泄露案件就达43 起，泄露包含用户个人信息数据的订单达上百万张[3]。目前部分快递公司采用的“隐形面单”，可以使他人无法直接从面单上看到个人信息，但是对快递公司、快递网点来说，个人信息依然裸露，快递员可通过扫描隐私面单的条形码或二维码来获取用户信息[4-7]。如果快递员居心叵测，仍然可以收集这些信息，造成用户信息泄露[8]。另外，采用“隐形面单”在某种程度上影响了递送效率，导致部分快递人员甚至一些快递公司不愿意使用这种快递面单，快递用户隐私信息仍然处于公开状态。针对以上情况，需要设计新的、方便使用的快递隐私面单来保护快递用户隐私信息的安全。

二是快递用户隐私信息的存储安全问题。目前快递公司每日收到数以万计的包裹，这些包裹的用户隐私信息直接存储于快递公司的服务器中，一旦监管不善，很容易出现内部人员“监守自盗”问题，甚至还有个别快递公司公然叫卖用户的个人信息以牟利。据报道，2017 年4 月，荆州公安机关就曾破获一起快递公司内部人员获取、贩卖快递用户隐私信息案件，涉嫌被泄露的快递用户信息达千万余条，涉案金额高达200 余万元，危害程度令人触目惊心[9]。对于快递用户隐私信息的存储安全问题，虽然快递公司加强了其信息系统的防护功能，在一定程度上降低了因系统不完善和黑客攻击造成的快递用户隐私信息的泄露风险，但仍然无法解决这种因快递公司管理人员“监守自盗”而造成的快递用户隐私信息的泄露隐患。因此，需要设计快递用户隐私信息保护机制来保护快递用户的隐私信息安全。

三是快递用户隐私信息在传输过程中的信息安全问题。快递公司的寄件终端在将快递用户隐私信息传输给服务器的过程中没有进行加密或采用加密强度不够的算法，容易造成快递用户隐私信息在网络上“裸奔”。此外，随着信息技术的发展，利用传统加密技术设计出的密钥生成算法在密钥空间扩展方面已不能满足当前数据加密算法的需求[10]，因此迫切需要一些新的密码技术对传输的快递用户隐私信息进行加密。混沌是一种非线性现象，混沌信号具有非周期性、初值敏感性、类似噪声以及不可预测性和连续宽带频谱等特征，这些特征恰好同密码学的基本要求相一致。如果能够对混沌的基本特性加以正确利用，通过易实现的简单方法就能获得具有高安全性的加密系统[11-12]。但目前混沌加密技术主要应用于电子商务安全加密[10]、图像加密[13-14]以及保密通信[15-17]等领域，将混沌加密技术应用于用户快递信息的隐私保护还未见相关文献研究。因此，可以尝试应用混沌加密技术来保障快递用户隐私信息在传输过程中的信息安全。

为了解决以上3 个快递用户隐私信息保护问题，本文拟提出快递面单生成方法、快递隐私信息保护机制模型和混沌加解密算法来保护快递用户隐私信息安全。

1 快递隐私面单生成方法

对于快递面单上的用户隐私信息保护问题，提出一种新的快递隐私面单生成方法，可有效保护用户个人隐私信息。

具体方法如下：用相应的数字对快递公司下设的省级快递点、市级快递点、区（县）快递点、街道（乡镇）快递点、社区（村）快递点进行编号。如将全国34 个省级快递点用01～34 个数字编号，市级快递点用2 位十进制数字依次从01 开始编号，区（县）快递点、街道（乡镇）快递点也是如此，社区（村）快递点较多，用3 位十进制数字依次从001 开始编号，如此可生成地址编号，再加上收件人（寄件人）手机号码的后4 位，便形成了包裹收件（寄件编号）编号4。

如表1所示，包裹收件地址是“江苏省扬州市广陵区东关街小厂社区”，将包裹收件编号按照以上包裹编号生成规则，江苏省在全国34 个省级行政区划中，编号为“23”，扬州市在江苏省内市级单位的编号为“03”，广陵区在扬州市下属区县中的编号为“02”，东关街道在广陵区的编号为“01”，小厂社区在东关街道的社区编号为“211”，收件人的手机号码后4 位是“8888”，因此该包裹的包裹收件编号为“230302011118888”，如表2 所示。同理，可生成包裹寄件编号150103042223333，如表3 所示。

表1 寄件人在寄件点App 上填写的信息

表2 包裹收件编号生成实例

表3 包裹寄件编号生成实例

2 快递隐私信息保护机制模型

针对快递用户隐私信息的存储安全问题和快递用户隐私信息在传输过程中的安全问题，提出了一种基于混沌加密的快递用户隐私信息保护机制模型，如图1 所示。

（1）寄件人到快递公司社区寄件点办理寄件业务，在寄件点App 上点击“邮寄包裹”按键，弹出填写收件人和寄件人信息的对话框。

（2）寄件点App 发送寄件请求给快递公司服务器。

（3）快递公司服务器生成包裹流水号（例如：为241），并回传给寄件点App。

（4）寄件人在寄件点App 上填写收件人和寄件人信息，如表1 所示。寄件点App 接收快递公司服务器生成包裹流水号“241”，同时将收件人地址信息和手机信息按照包裹编号生成规则生成包裹收件编号和包裹寄件编号，并与流水号进行匹配，生成如表4 和表5 所示的信息列表。

（5）为确保收寄件人信息在传输过程中的安全，寄件点App 采用混沌加密算法将表4 的核心信息——收寄件人手机号码的后6 位加密，发给第三方可信数据库，以确保手机这一核心隐私信息在传输过程中不被窃取。此处所采用的混沌加密算法将在第3 节加以介绍。

（6）寄件点App 将包含包裹流水号、包裹收件编号和包裹寄件编号信息的表5 发给快递公司服务器存储。

（7）寄件点App 打印出寄件面单，贴于包裹之上，包裹递送人员按包裹编号逐级投递到各快递点，最终到达社区收件点。各级快递点的快递人员只需知道寄件编号相应位上数字所对应的快递点信息即可，而不用知道收寄件编号其他位上数字所表示的含义。

（8）快递公司各快递点在包裹到达后，向快递公司服务器发送包裹的位置信息。

（9）包裹递送到快递公司社区收件点后，收件点APP发送如表6所示的信息给快递公司服务器。

（10）快递公司服务器收到表6 的信息进行存储，并转发给第三方可信数据库。

（11）第三方可信数据库收到信息后，通过对流水号所关联的包裹收件人电话号码采用混沌解密算法进行解密，并给该号码发送短信：“包裹已到最近的快递公司社区收件点，请速取！包裹流水号为‘241’！”此处所采用的混沌解密算法下文会加以介绍。

表4 发往第三方可信数据库的信息

表5 发往快递公司服务器的信息

表6 包裹递送到快递公司社区收件点后发往快递公司服务器的信息

（12）收件人收到取件信息后，到快递公司社区收件点，报包裹流水号和手机号码后4 位数字，快递公司社区收件点工作人员核对包裹流水号和包裹收件编号的后四位，如果匹配，则取件成功，取件人签收。

（13）快递公司社区收件点App 发送如表7 所示的信息给快递公司服务器。

表7 收件人取件后社区收件点App 发往快递公司服务器的信息

（14）快递公司服务器收到如表7 所示的信息进行存储，并转发给第三方可信数据库。

（15）第三方可信数据库收到信息后，对流水号所关联的包裹寄件人电话号码采用混沌解密算法进行解密，通过短信平台给该号码发送短信：“收件人已收到流水号为‘241’的包裹！”此处所采用的混沌解密算法将在第3 节加以介绍。

3 混沌加解密算法

本文拟采用混沌加密算法对寄件点App 终端发往第三方可信数据库的收寄件人的手机号码分别进行加密。第三方可信数据库收到包裹已到收件点的信息后，采用混沌解密算法对流水号所关联包裹的收寄件人电话号码进行解密。下面介绍所用到的混沌加解密算法。

3.1 混沌系列的产生

Logistic 混沌系统模型也称为“虫口模型”，是美国生态学家R.May 在分析昆虫种群个体数量和环境因素的关系时发现的，虽然形式简单，但却是一个典型的混沌系统，具有非常复杂的非线性动力学特征。其表达式如下：

式中，初始值x(0)∈(0,1)，μ∈(3.57,4]时，该系统处于混沌状态。

在该混沌系统的基础上，有人提出了二维成对Logistic 混沌系统[18-19]：

当2.75＜μ1≤3.4，2.7＜μ2≤3.45，0.15＜γ1≤0.21，0.13＜γ2≤0.15 时，该混沌系统为混沌映射，其中x(n)，y(n)∈(0,1)。

相较于Logistic 混沌系统，二维成对Logistic 混沌系统具有两个二次项，加强了其复杂性，可生成伪随机性更强的伪随机系列。本文选择二维成对Logistic 混沌系统来生成混沌系列，对收寄件人的手机号码进行加密。

混沌序列是在密钥设计结束后相继产生的，在混沌序列生成过程中，将初始值x(0)、y(0)、μ1、μ2、γ1和γ2作为密钥，用于产生混沌系列。

由于混沌系统的暂态效应，在使用二维成对Logistic 混沌系统产生混沌系列时，可让系统迭代一定次数之后，再使用生成的值，这样可以更好地掩盖原始信息的情况，具有更高的安全性。

3.2 混沌加密算法

由于收寄件人的手机信息是最为核心的敏感信息，应对手机号码后6 位采用混沌系列进行加密。加密算法如下。

（1）选择合适的密钥。K=(x(0),y(0),μ1,μ2,γ1,γ2)，产生混沌系列x(1),x(2),…和混沌系列y(1),y(2),…。

（2）混沌系列整数化，得到Xi和Yi。鉴于混沌的暂态性，选取混沌系列x(101),x(102),…和y(101),y(102),…用于加密。由于混沌系列是浮点数，因此不能直接对手机号码进行加密，可以将混沌系列值转化成6 位的整数，方法为：

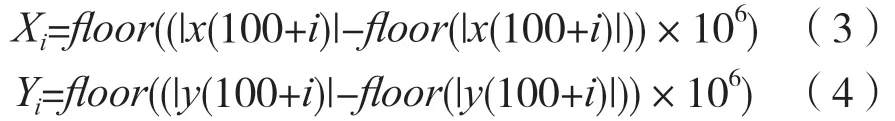
式中，floor()为向下取整函数。

（3）混沌系列二进制化，得到Ei和Fi。将6位十进制数进行转换，得到对应的20 位二进制数Ei=DECtoBIN(Xi)和Fi=DECtoBIN(Yi)，其中DECtoBIN()为6 位十进制数到20 位二进制数的转换函数。

（4）将收寄件人手机号码的后6 位转换成20位二进制数，得到Pi和Qi。令收件人手机号码的后6 位为Receiverphone，寄件人手机号码的后6 位为Senderphone，将十进制数转换成20 位二进制数Pi=DECtoBIN(Receiverphone)和(232)6=2192。

（5）采用异或运算Pi⊕Ei=Ci和Qi⊕Fi=Di对收件人和寄件人的手机号码进行加密，得到收件人手机号码的加密密文Ci和寄件人手机号码的加密密文Di。

3.3 混沌解密算法

第三方可信数据库收到包裹已到收件点的信息后，采用混沌解密算法对流水号所关联包裹的收寄件人电话号码进行解密。解密算法如下：

（1）在第三方数据库采用和加密密钥相同的密钥K=(x(0),y(0),μ1,μ2,γ1,γ2)和相同的二维成对Logistic 混沌系统，产生混沌系列x(1),x(2),…和混沌系列y(1),y(2),…。

（2）混沌系列整数化，得到Xi和Yi。鉴于混沌的暂态性，选取混沌系列x(101),x(102),…和y(101),y(102),…用于加密。由于混沌系列是浮点数，因此不能直接对手机号码进行加密。必须将混沌系列值转化成11 位的整数，方法如式（3）和式（4）所示。

（3）混沌系列二进制化，得到Ei和Fi。将6位的十进制数转换成20 位的二进制数，得到对应的二进制数Ei=DECtoBIN(Xi)和Fi=DECtoBIN(Yi)，其中DECtoBIN()为6 位十进制数到20 位二进制数的转换函数。

（4）采用异或运算Ci⊕Ei=Pi和Di⊕Fi=Qi分别对收寄件人手机号码的后6 位进行解密，得到二进制化的收件人手机号码明文Pi和二进制化的寄件人手机号码明文Qi。

（5）将二进制的收寄件人手机号码的后6 位还原成十进制。分别将20 位二进制数还原成6 位十进制数，得到十进制的收寄件人手机号码后6 位数Receiverphone=BINtoDEC(Pi) 和Senderphone=BINtoDEC(Qi)，其中BINtoDEC()为20 位二进制数到6 位十进制数的转换函数。

3.4 算法分析

3.4.1 安全性分析

（1）密钥空间分析。一个性能良好的加密算法必须要有一个巨大的密钥空间来抵御暴力穷举攻击。本文算法的密钥为二维成对Logistic 混沌系统的初始值和系统参数，即K=(x(0),y(0),μ1,μ2,γ1,γ2)。若计算机的计算精度为32 位,则该算法的密钥空间为(232)6=2192。即使攻击者以一次尝试时间为1 微秒的速度进行穷举攻击,也需要大约1.99×1044年。因此本文的算法有足够大的密钥空间来抵御暴力穷举攻击。

（2）密钥敏感分析。为增大破译者对密文的破译难度，应使得明文与密文之间的统计关系尽可能地复杂。在理想情况下，明文任意极小的变化都能使得密文按位以50%的概率发生变化[20]。密文对明文的微小变化越敏感，则算法的安全性越高。

为了测试密文对明文的敏感性，随机选取需加密的手机号码后6 位为“972516”，明文出现微小变化时的密文变化如表8 所示。可以看出，明文手机号码后6 位中的一位发生微小的变化，其密文变化较大，这说明该算法的密文对明文的微小变化较敏感，因而本文算法的安全性较高。

表8 明文存在微小差异的密文比较

（3）密文分布分析。密文分布是加密算法安全性的重要指标之一。如果加密算法得到的密文分布不均匀，密码攻击者就能通过唯密文攻击来对密文进行破译。理想状态是加密后的密文流中0 与1的个数应相等[20]。下面分别选取不同个数的明文（手机号码后6 位）经过加密后得到密文，比较其中0和1的个数分布情况，如表9所示。从表中可以看出，不同个数的明文经加密后得到的密文中0 和1 的个数相差不大，因此该算法能有效抵御唯密文攻击。

表9 密码分布分析

3.4.2 性能分析

一个加密算法的性能主要取决于两个方面：一是算法的计算量小，在相同硬件条件下，加密所耗费的时间较短；二是算法运行所耗费的存储空间较少。下面从这两个方面来分析该算法的性能。

（1）运算时间方面。该算法的计算量主要包括伪随机序列生成所耗费的时间T1、伪随机序列与电话号码进行异或运算的时间T2，其时间复杂度为O(n)=T1+T2，时间复杂度为一次线性函数，时间复杂度较小，大大提高了运算效率。

（2）存储空间方面。在运算过程中需要将伪随机序列和电话号码临时存储，且该算法是进行一次性加密，无须在加密过程中进行迭代，减少了加密过程中数据的存储环节，所以所需的存储空间相对较小，减小了空间复杂度，实现了加解密过程的高性能。

综合以上分析，该算法所耗费的时间较短，所占用的存储空间相对较少，因而具有良好的性能。

3.5 算法比较

和一些用于文本加密的混沌算法相比，本文提出的加密算法一个最突出的优点是具有较大的密钥空间，因而具有更强的抵抗暴力穷举攻击的能力。表10 是对几篇文献中混沌加密算法密钥空间和穷尽密钥空间所需时间的比较（假设计算精度为32位，攻击者以一次尝试时间为1 μs 的速度进行穷举攻击）。可以看出，该算法的密钥空间要比已有算法的密钥空间大得多，抵御暴力穷举攻击的能力也较强。

表10 穷尽密钥空间所需时间

4 结语

本文通过将省级快递点、市级快递点、区（县）快递点、街道（乡镇）快递点、社区（村）快递点用相应的数字编号，提出了一种快递面单生成方法，可有效保护快递面单上的用户隐私信息，同时可避免传递过程中各级快递员知悉快递用户的隐私信息。此外，提出了一种快递用户隐私信息保护机制，使快递公司无法掌控快递用户信息，可有效避免快递公司对快递用户隐私信息“监守自盗”和黑客对快递公司数据库攻击而造成的泄露快递用户隐私信息的隐患。另外，提出了一种混沌加密算法，用于加密快递用户隐私信息，可有效保证快递用户隐私信息在传输过程中被窃取而泄露。