高阶QAM解映射方法研究与实现*
王 维
(中国船舶集团有限公司第八研究院,江苏 南京 211100)
0 引言
为了提高通信速率,现代通信协议都在努力提高单位发射符号所能携带的比特数量。例如,4G 标准中使用256-QAM(Quadrature Amplitude Modulation,正交幅度调制),5G 标准中升级为1024-QAM[1],与此同时,WiFi5 中的256-QAM 在WiFi6 时代亦升级至1 024-QAM[2]。
映射的复杂化同时也导致解映射的复杂化,因为现代通信系统中解映射的结果都不是确定的比特流,而是一种概率信息,它可以帮助译码器对解映射的结果进行纠错。通过概率信息进行信道译码的方法称为“软译码”。流行的信道编码算法,如Tubo 码、LDPC 码、极化码等均采用软译码,因而如何用较少的计算量完成复杂星座的解映射,并使其结果与理想的概率算法相符,是现代通信发展中需要解决的一项关键问题。
本文主要针对高阶QAM 映射方式,提出一种简化的映射/解映射方法,同时提出了一种信息处理方法,使最终的解映射结果符合信道译码对软信息的理论要求。全文共分4 部分论述,第1 部分给出了一种简化的高阶QAM 映射与解映射方法,第2 部分给出了将解映射结果转化为软信息的方法,第3 部分对本文改进的方法进行了仿真,并与理论算法进行了计算量和性能对比,最后对本文工作进行了总结。
1 映射和解映射方法
对于q-QAM 映射方式,一个映射星座包含的比特数为log2q,映射的星座点总数为q个,实部或虚部上的映射点各个,正负对称。映射时,先将所有待映射比特平均分为2 组,分别设为A 组和B 组,每组可独立决定n个比特的映射位置,满足n=。A 组的所有比特以实部为基础,B组的所有比特以虚部为基础。
映射时常用方法是在A/B 组内部按输入数据的顺序编排星座位置,即输入0,1,2,…,n,就直接对应星座位置由负到正排序[3],或先将输入数据按格雷码重新排序,然后按照格雷码顺序编排星座位置[4]。它的优点是直观,映射时不需要编排星座,但增加了解映射的复杂度,解映射器件中需要保存多张重排序列表。本文介绍一种新方法,打破原有的排序规则,按照方便解映射的方式进行映射,此方法也涉及重排序,但一种QAM 只需要1 张重排序表。具体映射步骤如表1 所示。首先按轴线方向由负到正罗列全部可能的星座位置,设为D(1)。然后对D(1)进行第1 次变换,其中且|D(n)|表示集合D(n)中全部元素的绝对值。以同样方式进行第2 次到第n-1 次变换。D(1)~D(n)共计n行,由此可得到数据和星座的映射关系。例如,表1 数据第1列均为负数,负数代表比特0,因此星座点-(a-1)对应的数据即为n个0 比特组成的数,即数据0。
值得注意的是,按照本文的方法进行映射,推导过程中会自然形成中心对称和轴对称两种关系。例如,D(2)的计算过程,以a/2 为被减数,得到的D(2)在正负轴上均以|a/2|的奇数倍坐标为中心对称,以其偶数倍坐标为轴对称,最后的D(n)以2 为被减数,相应的,以|2|的奇数倍坐标为中心对称,以其偶数倍坐标为轴对称。依据此规律,推导过程可只进行一半,其余可按照对称关系直接写出,进一步简化了推导过程。
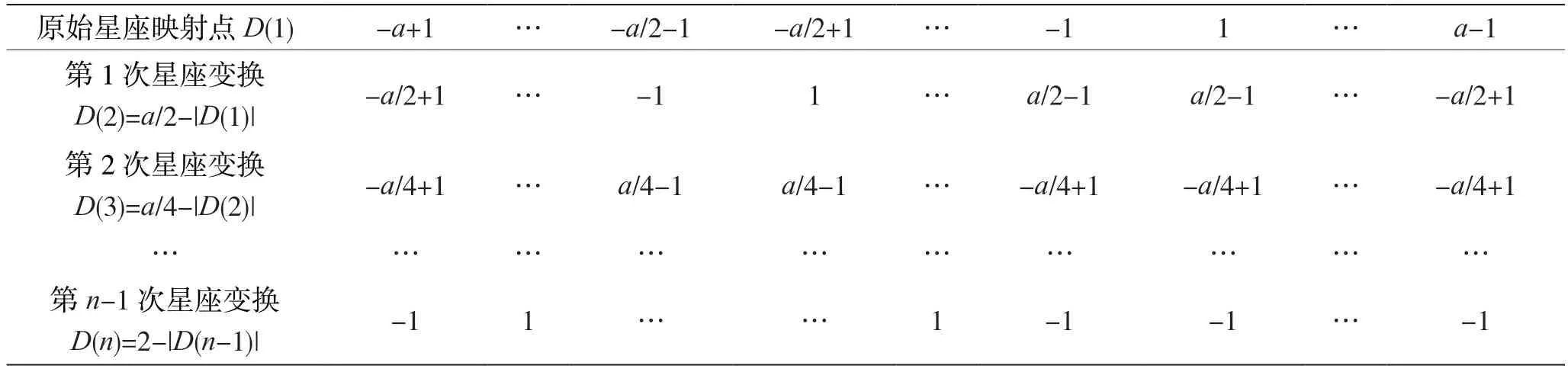
表1 改进方法的映射关系确定步骤
解映射方法与映射方法相似,设接收星座的实部为R,虚部为I,根据映射关系,以R为依据可解出前n个比特,以I 为依据,使用相同方法可解出后n个比特。下文以R为例描述解映射方法。解映射后输出的是软信息,该信息若为负数则表示该比特为0 的概率较大,反之则表示1 的概率较大。
第1 比特由于映射时是以坐标原点为界进行区分的,如图1 中D(1)所示,因此R本身即可作为软信息。设第1 比特的软信息为P(1),则P(1)=R。
第2 比特软信息为P(2)=a/2-|P(1)|,以此类推,第n比特软信息为P(n)=2-|P(n-1)|。表2 反映了4 096-QAM的解映射过程,其中R为接收信号的实部。

表2 4 096-QAM 的解映射
2 解映射信息的再处理
信道译码器的输入要求为对数似然比信息(Log-Likelihood Ratio,LLR)[5],其计算式为:
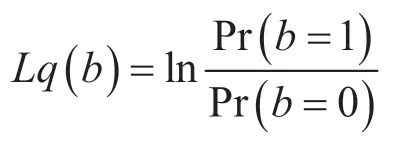
式中,b表示译码器输入的任意比特,Lq(b)为比特b的对数似然比信息,Pr(b=y)表示该比特b等于y的概率。
上文的解映射过程并未严格遵守LLR 的定义,因此需要对解映射结果进行再处理。但若严格依据定义,则不仅需要求解对数,随着QAM 星座的增加,Pr(b=y)的计算量也相应增加。本文提出一种用简单运算逼近理论计算的方法,其流程如图1 所示,其中x为比特序号,E(·)为转换过程的中间值。流程以解映射的结果P(x)开始,选取了3 个非线性点,分别是8、24、48,通过加入乘性因子以期逼近理论值。
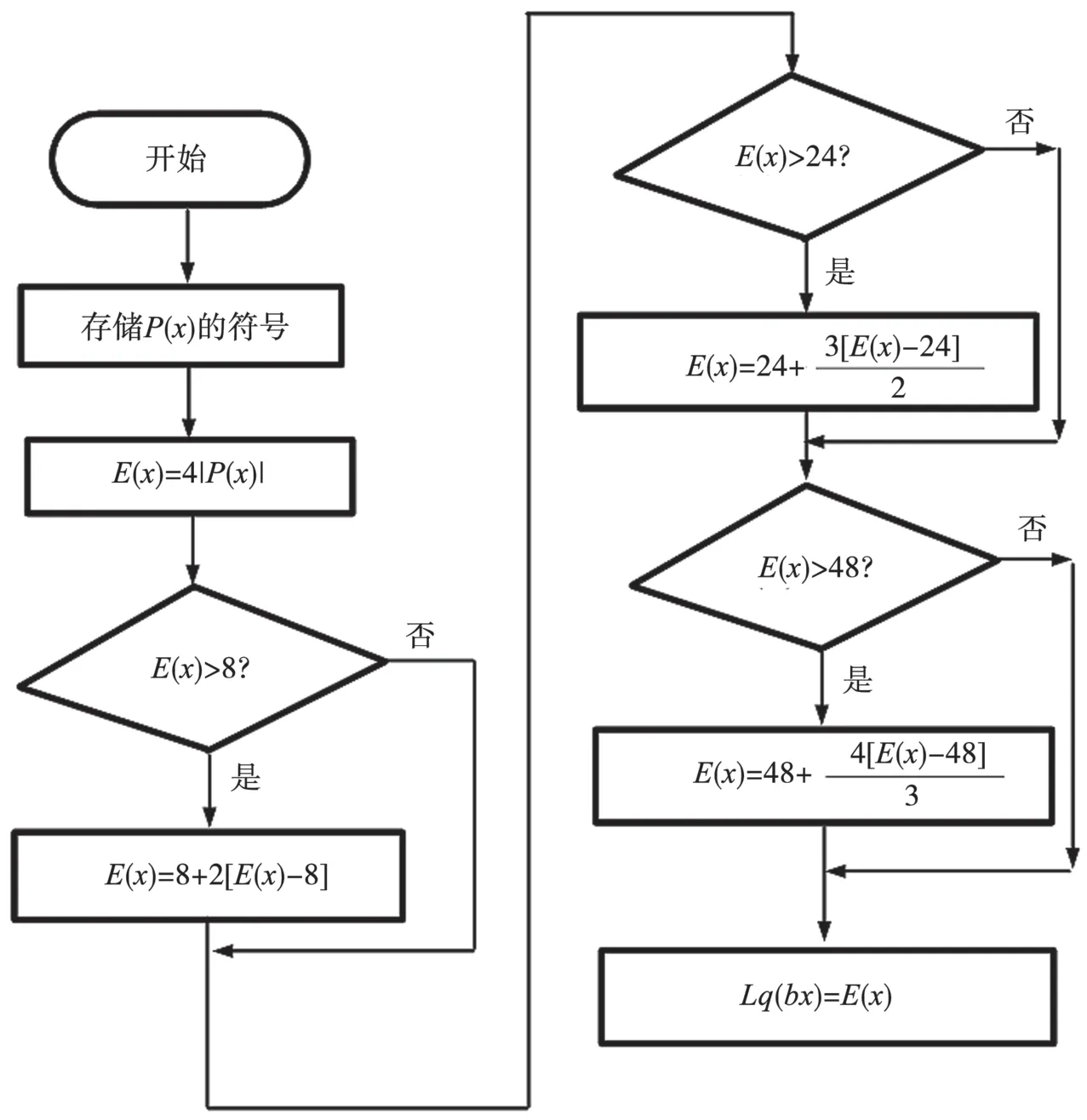
图1 解映射后处理流程
解映射的计算量因比特的位置而异,A 组和B组的最后一个比特所需运算量最大,共需n-1 次求绝对值和n-1 次加法,以1024-QAM 为例,它的第5 比特和第10 比特需要最多运算量,均为4 次求绝对值运算和4 次加法运算。而对于后处理过程,1个比特共需1 次绝对值计算,3 次比较运算,流程中的加法和乘法次数因比较结果不同而异,最多为4 次乘法和6 次加法。综上,对于1 个比特的解映射和后处理的计算量上限合计为:n次绝对值计算,n+5 次加法,4 次乘法,以及3 次比较。
理论计算的计算量包括4n-2 次加法,2n次乘法,1 次除法,2n次指数运算,1 次对数运算。电路实现中通常以查表法代替指数运算和对数运算,查表精度也会影响到最终数据的准确度。与本文改进方法不同,理论运算量对于所有比特都是相同的。可以看出,本文提出的方法,运算量相对于理论和其他方法有明显减少。
3 实验结果与性能比较
图2 给出了对1 024-QAM 使用此方法与理论方法处理的对比。其中,“*”线为理论方法,实线为本文提出的方法。可见,对于比特1,两者在变化幅度上有一定差别,对于其他比特,差别仅存在于星座严重偏离其映射位置的情况,此例映射最大坐标是31,而此范围内,理论和改进方法所得结果基本重合,对于接收星座偏离映射区域较远的情况,如图中|R|>32 区域,通信设备一般采取降低QAM 阶数的方式,因而,这一区域的差别可忽略。比特1 上的差别主要源于其提供了最丰富的纠错信息,从图中纵轴可以看出,比特1 提供的软信息范围是0~600,软信息量随比特序号增加而递减,比特5 提供的信息范围仅为0~40。改进方法在比特1 上的斜率小于理论方法,对译码过程的影响是在一定程度上降低了译码器的纠错收敛速度,增加了译码器的迭代次数,这也是为逼近其他比特的理论值而在比特1 上付出的代价。

图2 1024-QAM 的LLR 理论值与本文改进方法的对比
4 结语
本文对高阶QAM 的映射和解映射方法进行了研究,提出了一种简单实用的改进方法。该方法在计算方面仅采用基本四则运算和求绝对值,相对于普通的求对数似然比法,计算量明显减少,且普通理论方法对于不同阶数的QAM,计算公式有所区别,而使用本文改进方法,对于不同阶数均使用同一法则,这是对映射器件的进一步简化。在解调性能方面,改进方法的结果接近理论值,由于第1 个比特的解存在差异,译码收敛速度会稍慢于理论方法。

