横风对受电弓各杆件气动特性的影响研究*

赵 萌，刘美英，贾 彦，刘晓禹，王益鹤

（1 内蒙古工业大学能源与动力工程学院，呼和浩特 010051；2 北京城建亚泰建设集团有限公司，北京 100013）

高速列车受电弓与架设在轨道上方的高压接触网可靠地接触是保证高速运动的重要条件[1]。横风作用于高速列车时，由于受电弓结构复杂，且迎流角度均有不同，各杆件气动力差异显著，加剧了受电弓的横向摆动，分离涡中心线发生偏转，对受电弓运行的安全性和寿命造成威胁[2-5]。国内外专家学者针对横风作用下对高速列车气动特性做了大量的研究，王政等[6]通过数值计算的方法，探究高速列车在均匀风和指数风下气动特性；BAKER等[7]在风洞中进行各工况的实验，分析了横风作用下的气动性能；POMBO等[8]利用数值分析横风作用下弓网的气动特性；柳润东等[9]研究了在不同横风风速和不同列车车速下单侧风障内列车交会对风障的冲击过程；龚明等[10]研究在横风作用下高速列车的外形优化；韩运动[11]等采用数值模拟方法，在不同横风风速和风向角的前提下，研究高速列车周围的压力和速度变化。但是目前针对受电弓各个杆件横风作用下气动力差异研究较少，且对各杆件绕流场特性欠缺深入研究。因此有必要对受电弓杆件气动特性深入探讨，分析在不同工况下受电弓各个杆件绕流特性的差异及最不利与运行安全的工况，为受电弓运行安全性、减振减阻等提供参考依据。

1 计算模型和计算方法

1.1 物理模型

首先对受电弓的支架和底架部分进行简化，以便分析受电弓主要杆件的气动特性，其几何外形如图1所示。受电弓的简化模型由上臂杆、滑板、支架、下臂杆、推杆、底架共6部分组成，同时建立接触网模型以保证计算的准确性，计算模型和计算域如图2和图3所示。

图1 简化受电弓的几何外形

计算模型包括列车组、受电弓及接触网，列车组模型由3节单独列车组成，分别为头车、中车以及尾车，其中3节列车宽度都为3 m，中间列车长为25 m，其余为25.7 m。图4为网格划分情况，网格数量为1.4×107，同时将列车表面、受电弓等流场进行局部加密。

图2 受电弓-接触网-列车模型

图3 弓-网-车模型的计算域

1.2 计算方法

数值模拟采用雷诺时均（RANS）方法，能够体现出湍流下平均流场的变化情况[12]。采用SSTk-ω模型，该模型结合了k-ω原型和k-ω模型的各自优点[13-14]，模型方程如式（1）和式（2）：

式中：下标i,j=1，2，3；D/Dt=∂/∂t+ui∂/∂xi；τij为湍动剪切应力；k为湍流动能；ω为涡量脉动强度；σk、σω、β、β*、γ为SSTk-ω模型的常数，其中，κ为常数；vt、μt为涡黏性参数；F1为混合函数。

1.3 计算方法的验证

由各杆件组成的受电弓，杆件中的上臂、下臂、推杆和底座等部件均为是钝体，通过RANS方法对钝体进行数值计算探究[15]，以验证本文计算方法的准确性。

选用的Ahmed模型如图5所示，其数值模拟的边界条件为：Pressure-outlet，Velocity-inlet入口速度设定为60 m/s，且钝体表面无滑移，网格的划分如图6所示。

Ahmed钝体表面压力分布图7所示，与文献[13]实验值相比较，文献中阻力系数Cd=0.285、摩擦阻力系数Cr=0.055，数值模拟为Cd=0.282、Cr=0.054，误差分别为1.05%、1.82%。由此可见，结果与文献结果误差在合理的范围内，说明RANS方法的适用性与准确性。

1.4 计算条件

计算域的入口设置为velocity，出口设置为pressure，相对大气压0 Pa。沿+x方向的速度分量为车速，大小为350 km/h；沿+z方向速度分量为横风风速，速度由10 m/s到30 m/s，间隔5 m/s；风向角为10°至90°，间隔10°。列车沿x轴正向运动，即主流风向沿x轴负向，横风方向沿z轴正向，横风、横风方向角分别用Vw、θ表示，β为偏航角，如图8所示。

2 计算结果与分析

2.1 受电弓绕流场特性

在横风作用下主流与受电弓主体结构纵向截面具有某一夹角，合成速度方向与运行方向不平行，受电弓横向、纵向绕流流场的叠加作用导致驻点位置改变。合成来流绕受电弓各杆件形成分离涡，不同尺度的分离涡的中心线发生不同角度偏转，涡的脱落和附着方位改变，受电弓各杆件绕流流场相互作用而产生的影响发生改变，对周围空气的扰动加剧。当横风的风速、风向角增大，偏航角即增大，受电弓各杆件受到横向扰动增强，接触网与列车的横风效应更加明显，绕流场的偏转对受电弓影响显著。上、下臂杆自身具有不用的空间攻角，其绕流特性具有差异性。以列车车速350 km/h、风向角30°、60°，横风风速20 m/s、25 m/s和30 m/s为例，分析受电弓绕流场特性。

图9为各工况表面压力和速度流线的分布，图9（a）中，随着横风风速与偏航角增大，接触网前方流场扰动加强，对滑板影响加强，出现较大范围的低速区。图9（b）与（a）相比较可见，当风向角为60°时受电弓底座周围绕流扰动增强，从而影响到下臂杆的流场，受电弓后方低速区范围增大。随着横风和风向角的增大，上臂杆和滑板压力明显增大。

图4 网格划分

图5 Ahmed几何模型

图6 Ahmed钝体的网格划分

图7 表面压力云图

图8 风向角的定义

图10为各工况受电弓横截面表面涡量线，滑板和滑板支架扰动剧烈，滑板两侧涡量扰动尤为明显，涡量出现最大值。图10（a）和（b）相比可见，随横风风速、风向角的增大，受电弓后方尾流区域中，涡量逐渐增多并向背风侧偏移。

图9 受电弓的表面压力和流线分布

图10 受电弓横截面表面涡量线

图11为各工况受电弓纵向截面压力分布，当风速以及风向角变大，导流罩的低压区范围变大，进而会影响到底座周围的压强分布。由图11（b）可知，随着风速变大，受电弓附近低压区范围变大，图11（a）和（b）相比较可见，随着风向角增加，受电弓尾流区的高压区逐渐减小。

图11 受电弓纵向截面压力分布

2.2 受电弓杆件的气动分析

分析不同工况下受电弓各气动特性参数指标，其中列车运行速度350 km/h，横风风速由10 m/s到30 m/s，间隔5 m/s；风向角为10°至90°，间隔10°。图12～图14为受电弓滑板的气动作用力系数，由图可见滑板的阻力系数随着风速、风向角成正比，当风速为30 m/s和风向角为90°时，阻力系数达到最大。风速在20 m/s到30 m/s时升力系数呈现上升后迅速降低，在35°附近出现升力系数最大值，而15 m/s的风速下，升力系数基本不发生变化。侧向力系数与风速和风向角呈正比的线性关系，风速越大侧向力系数越大，最大值在30 m/s的风速下，风向角在90°附近。滑板的阻力系数以及侧向力系数与受电弓相比，数值较小但规律基本相似。升力系数受风速影响较为明显，应重点研究滑板部分的升力。

图12 阻力系数变化曲线

图15～图17是受电弓上臂杆气动特性曲线，由图可见阻力系数随着风速和风向角呈正比变化，当风向角和风速达最大值时，阻力系数达到最大。升力系数随着风向角和风速呈反比关系，其值均为负值，在风速为15 m/s和20 m/s条件下，随着风向角的变化，升力系数呈现出近似线性的变化规律；在风速为25 m/s和30 m/s条件下，则成余弦规律变化。侧向力系数随着风向角和风速增大而后增大，最大值出现在30 m/s下，风向角为30°时。由此可见，各杆件升力系数变化规律复杂，在受电弓运行过程中应重点考虑。

图13 升力系数变化曲线

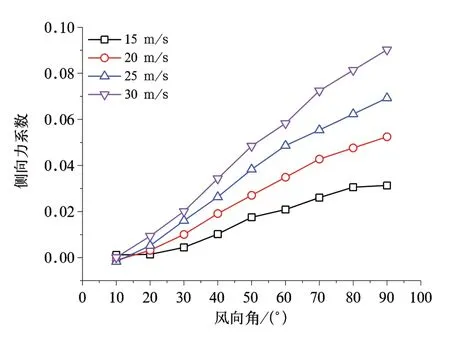
图14 侧向力系数变化曲线

图18～图20为下臂杆的气动特性曲线，由图可见下臂杆阻力系数随风向角和风速成正比，升力系数为负值，随着风向角增大升力系数则减小。侧向力系数和阻力系数呈现的规律基本一致。由此，可以看出阻力系数以及侧向力系数与受电弓相比，数值较小但规律基本相似，升力系数与受电弓相比，作用力方向相反。

图15 阻力系数变化曲线

图16 升力系数变化曲线

图17 侧向力系数变化曲线

图18 阻力系数曲线

图19 升力系数曲线

图20 侧向力系数曲线

图21～图23为受电弓各杆件所受气动力占总作用力的份额，由图可见滑板的阻力、升力以及侧向力占比最大，下臂杆的阻力、升力以及侧向力占比最小。随着风向角增大，滑板阻力和升力占比减小；上臂杆和下臂杆阻力占比增加，而升力占比则减小。风向角为60°以后，上、下臂杆阻力占比稳定在26%和1.5%左右；随风向角的增大，滑板的阻力占比减小，风向角为60°以后占比稳定在40%左右。上臂杆由于所受升力方向与总作用力相反，占比额以负值表示。

图21 阻力份额图

为了得到阻力、升力、侧向力的规律，将滑板、上臂杆、下臂杆与受电弓阻力、升力、侧向力的比值分别为Δcx、Δcy和Δcz，符号参数之间的关系如下：

图22 升力份额图

图23 侧向力份额图

上式中i=1，2，3代表滑板、上臂杆和下臂杆；cx、cy、cz为受电弓的阻力系数、升力系数和侧向力系数。计算各部件作用力系数与总作用力系数的比值如表1所示。

表1 各部件作用力系数与总作用力系数的比值

由表1可知，滑板的Δcx最大，下臂杆的Δcx最小，滑板的阻力在总阻力中的占比最大，上、下臂杆的Δcx随风向角的增大而增大。在升弓姿态下，由于各杆件的空间角度等参数不一致，导致力作用的规律不同。上臂杆的Δcz最大，当风向角处于10°到50°之间，上臂杆与滑板的Δcz值为负，风向角处于50°时绝对值最大。因此，受电弓上部构件受横风和风向角产生较大影响。

3 结论

（1）随着风速和风向角的增大上臂杆和滑板压力呈正比，导流罩的低压区范围变大，进而会影响到底座周围的压强分布，受电弓尾流区高压区范围减少；滑板和滑板支架处绕流尤为强烈，涡量较多，在尾流区分离、破裂，向横风背风侧偏离。

（2）对于受电弓的滑板、上下臂杆的阻力、侧向力系数随风向角和横风风速的增大成正比；上、下臂杆升力系数为负值，与受电弓相比作用力方向相反，其中上臂杆在横风风速为25 m/s和30 m/s条件下升力系数成余弦规律变化；下臂杆升力系数随着风向角增大则减小。

（3）滑板的阻力在总阻力中的占比最大，上、下臂杆的Δcx随风向角的增大而增大。在升弓姿态下，由于各杆件的空间角度等参数不一致，导致力作用的规律不同。上臂杆的Δcz最大，当风向角处于10°～50°之间，上臂杆与滑板的Δcz值为负，风向角处于50°时绝对值最大；风向角处于60°～90°下，下臂杆Δcz为负值。

（4）受电弓上部构件受横风和风向角产生较大影响，故在横风工况下应首先保证上部构件稳定性；通过对不同工况的分析，由于各个杆件自身的空间攻角与横风风向角的叠加，保证受电弓安全性不能以最大横风和风向角为标准，在复杂工况中首先应满足滑板升力的安全范围。