改进Canny算子的列车轮对踏面边缘检测算法

刘成刚，刘二林，姜香菊

（1 兰州交通大学 机电工程学院，兰州 730070；2 兰州交通大学 自动化与电气工程学院，兰州 730070）

随着列车运行的高速化和重载化的增加，轮对踏面损伤现象日益频繁，轮对踏面出现损伤会导致轮轨间的冲击力瞬间升高，从而严重威胁到高速列车的运行安全和车轨设备的安全和使用寿命[1-2]。自上世纪80年代初，国内外专家和学者对轮对踏面的损伤在线检测方面做了大量研究，并取得丰硕成果。起初罗马尼亚研制了车轮外形磨耗自动检测装置，并对获取的图像进行分析，由于受到图像采集速率与数据处理能力的限制，该系统只适用于低速检测。后续欧美等国家相继采用振动加速度法[3]和冲击载荷法等[4]对轮对踏面进行分析研究。国内研究起步较晚，采用非接触光电检测方法[5]、压电加速度传感器[6]、振动加速度法、超声波探伤法[7]和平行四边形法等对轮对踏面损伤情况进行检测。其中振动加速度技术安装结构简单，但是测量精度低；超声波技术测量效果好，但技术难度大，其他检测方法也出现了不同程度的局限性。为此，机器视觉技术的发展为之提供了一种切实可行的检测方法。文中提出一种改进的Canny算子，该改进的算法能够有效的保留更多踏面边缘信息，并抑制虚假边缘，从而很大程度上将踏面损伤真实情况再现，并且避免了人工漏检、误检问题，同时也为高速列车安全运行提供有效保障，所以具有十分重要的研究意义与实际应用价值。

1 Canny算子边缘检测算法

1.1 Canny算子的理论基础

John F .Canny在1986年提出了一种多级边缘检测算法[8-9]，该算法是高斯函数的一阶导数，是对信噪比和定位精度之乘积的最优逼近算子，在处理含有高斯噪声图像得到广泛应用[10]。根据优良边缘检测算子的3个准则来评价该算法的优越性。

(1）最佳信噪比准则：即低错误率，所有的真实边缘被准确判断，将虚假边缘误判的概率尽可能的小。信噪比越高则越好。

(2）高定位精度准则：即已经检测到的边缘点应该与真实边缘点之间的距离最小。

(3）单一边缘响应准则：即单个边缘点只响应一次，不能产生多次响应，最大限度的抑制虚假边缘响应。

1.2 Canny边缘检测算法步骤

(1）高斯滤波平滑处理图像即消除噪声，用二维高斯函数对灰度图像f(x,y)进行卷积运算，从而得到平滑图像I(x,y)，见式（1），高斯函数表达式见式（2）：

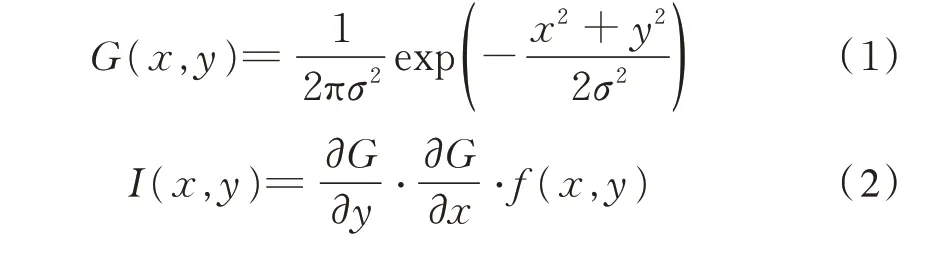
式中：σ为方差，会影响定位精度和信噪比，且控制着图像的平滑程度[11]。

(2）计算梯度幅值和方向，传统的Canny算子用2×2领域内一阶偏导的有限差分来计算经高斯平滑处理后图像I(x,y)的梯度幅值M(x,y)和方向θ，分别见式（3）、式（4）：

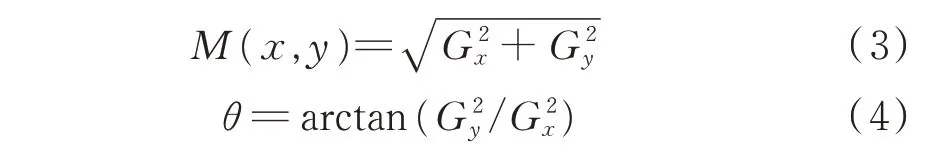
式中：梯度分量Gx、Gy的确定分别见式（5）、式（6）：

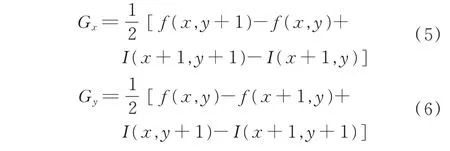
(3）梯度幅值非极大值抑制（NMS，non-maximum suppression），用来排除非像素点，判断像素点的灰度值在其8领域内是否最大，若是，把该像素点作为候选的边缘点；反之，将M(x,y)灰度值置0，剔除非边缘点[11]。

(4）双阈值算法检测和连接边缘，经非极大值抑制可得到梯度幅值矩阵，人为的设定初始高低阈值Th和Tl，根据所设定的高低阈值将梯度图像分为2个阈值边缘图像，由高阈值分割后的图像，不包含虚假边缘，但是图像轮廓有间断，所以采用低阈值来弥补高阈值带来轮廓边缘间断的缺陷，直到用高阈值分割后的图像轮廓边缘闭合为止，进而得到低阈值边缘图像[12-13]。

2 改进的Canny算子

2.1 双边滤波

在采用传统的Canny算子对图像滤波去噪时，由高斯滤波函数可知，其方差σ在处理不同图像时，需要人为的设定不具有自适应性，所以会导致图像边缘信息的模糊化，进而使整个图像模糊不清，同时还会丢失大量的边缘信息。为了克服以上问题，文中采用的双边滤波算法代替高斯滤波，在滤波去噪的同时还能保留大量的边缘信息[14]。

双边滤波（bilateral filter），具有双重滤波作用，是1种非线性的滤波器，相比高斯滤波器多1个高斯方差，在处理区域内相邻各像素值时，同时考虑到各像素值几何邻近关系和亮度上的相似性，然后将二者非线性组合，自适应滤波后达到保留边缘去除噪声的目的[10]。

双边滤波器领域像素值的加权值组合决定了输出的像素值，对含有噪声的图像p(i,j)处理后的图像为g(i,j)，见式（7）：

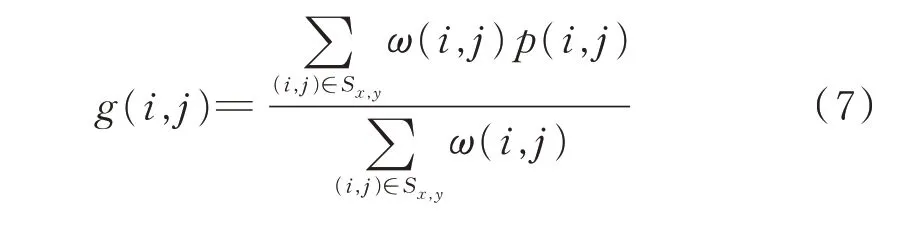
式中：p(i，j)为输入图像；g(i，j)为输出图像；Sx,y表示像素中心点(i，j)的（2N+1）×（2N+1）领域大小；ω(i，j)为权值，其包含两部分：ωs(i，j)和ωr(i，j)，分别见式（8）、式（9）：

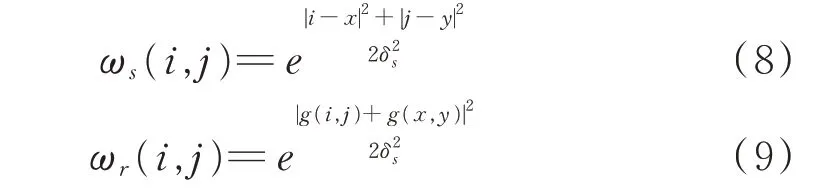
由二者得到ω(i，j)=ωs(i，j)ωr(i，j)。

2.2 梯度幅值和方向计算的改进

现有的Canny算子在计算图像梯度幅值时采用2×2领域一阶有限差分运算，只考虑到水平和垂直方向上的梯度值，因此易受到来自外界噪声的干扰，检测出虚假边缘，检测效果不佳。冯永亮[12]、王植[15]等人在传统的Canny算子在x方向、y方向梯度模板基础上又加入45°和135°方向，对4个方向做一阶有限差分来计算梯度幅值，经分析对比发现，对噪声干扰有一定的抑制作用，但是计算复杂，相对效率低。借鉴文献[16-17]提出的算法，在Soble算子的基础之上加入45°和135°方向来计算梯度幅值。在3×3领域内4个方向上的梯度模板见式（10）：

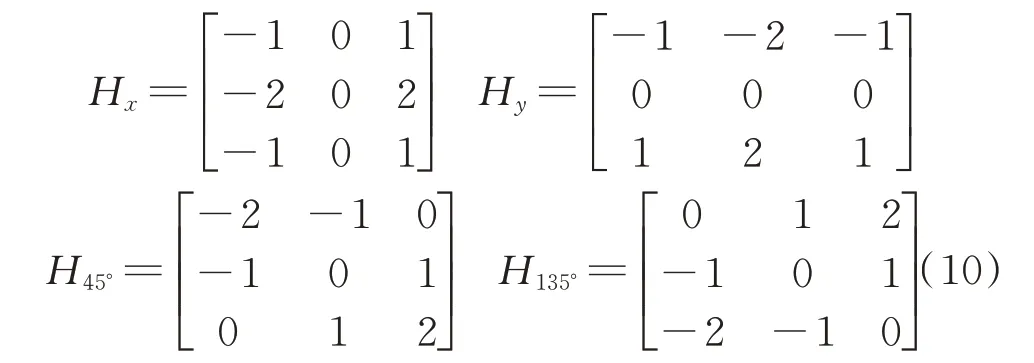
将水平方向、垂直方向、45°方向、135°方向的梯度模板Hx、Hy、H45°、H135°分别与滤波后的图像进行卷积运算，得到4个方向上的梯度分量Mx、My、M45°、M135°，最后求得梯度幅值M，见式（11）：

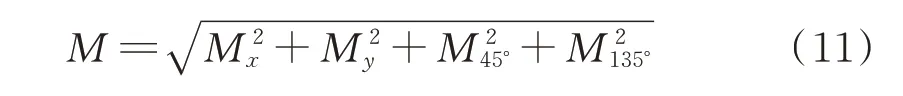
由4个方向上的梯度分量合成到水平和垂直2个方向上总的梯度分别为Mx、My，分别见式（12）、式（13）：

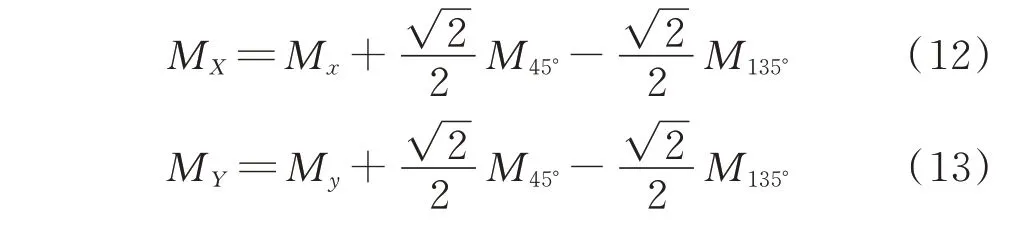
由MX、MY求得梯度方向δ，见式（14）：

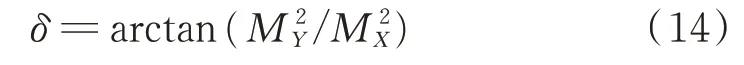
2.3 Otsu算法求高低阈值

Otsu算法，又称大津法，是由日本学者大津展之提出的一种对非极大值抑制后的梯度图像进行阈值分割的一种算法，其可以自适应的确定阈值，从而避免了人为设定高低阈值的缺陷。此算法将图像按照灰度分为前景和背景两类，若目标图像大小为M×N，其中含有L个不同灰度等级，Otsu法将在像素灰度0～(L-1)范围内计算对应的方差，通过不断比较，最终获得前景与背景间的最大间类方差，所以又称为最大间类方差法[18]，方差越大，则分类就越正确。

在含有L个不同灰度等级的M×N图像中，每个灰度值对应的像素值为ni，i∈[0，L-1]，则其中某一像素i所出现的概率为pi，见式（15）：

假设选择1个阈值k，k∈[0，L-1]，将图像像素灰度分成2类，即前景W0和背景W1，二者灰度等级范围分别为：W0∈[0，k]，W1∈[k+1，L-1]。因此，某一像素落在W0、W1上的概率分别为PW0(k)、PW1(k)，分别见式（16）、式（17）：

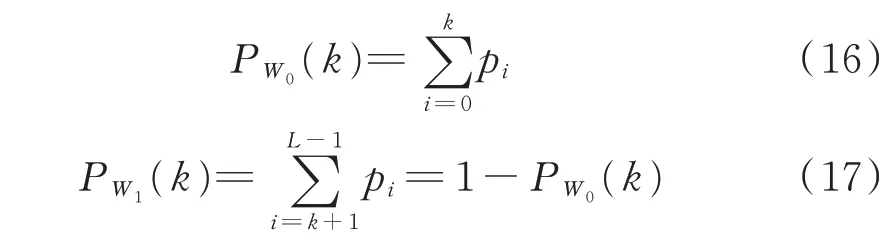
前景W0、背景W1平均灰度值分别为h0(k)、h1(k)分别见式（18）、式（19）：

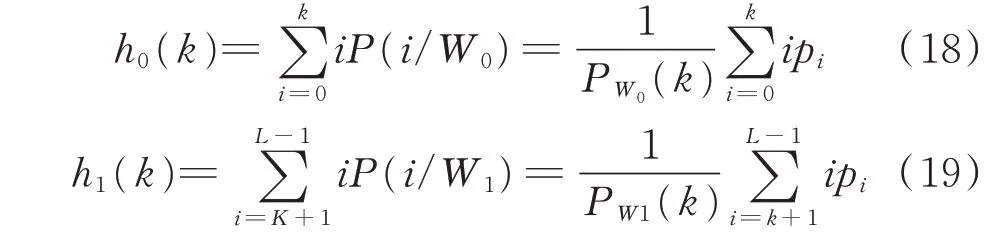
则整个图像的平均灰度值为h(k)，见式（20）：

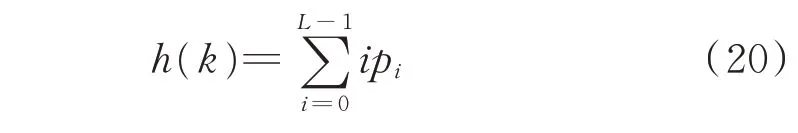
由上述公式可求得前景W0和背景W1间的最大间类方差δ2，见式（21）：

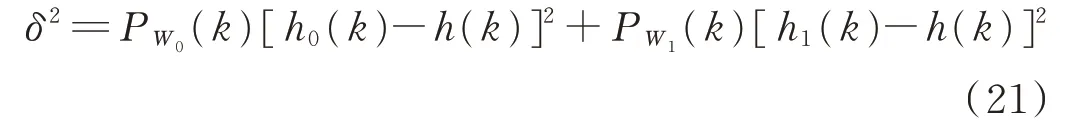
在不同的k值下求间类方差，当间类方差δ2取得最大值时所对应的k值就是所求得的最优阈值，将此最优阈值设为高阈值Th，低阈值为Th/2。在改进的Canny算法中用Otsu法自适应求取阈值来代替人为设定高低阈值，从而增强了整个算法的自适应性，使得图像边缘信息提取更加完整、清晰。

3 仿真实验结果分析

3.1 原始灰度图像处理分析

为了验证改进的Canny算法相对传统Canny算法在保边去噪方面的优越性，在某铁路局检修作业车间在线采集系统上，选择其中一张采集到的轮对踏面图像在Matlab 2019a环境下进行仿真分析验证，仿真时，采用传统Canny算法处理时选取Th=100，Tl=80，仿真实验结果如图1所示：

图1 原始图像仿真实验结果

图1中的图1(a)是采集到轮对踏面的部分原始灰度图像，图1(b)是经过双边滤波算法平滑滤波后的图像，图1(c)是采用传统的Canny算子处理过的踏面图像，图1(d)是采用文中算法对原始灰度图进行处理；图1(c)和图1(d)相比，图1(d)中轮对踏面损伤部位细节更加明显，轮缘轮廓线也更加清晰完整，具有良好的单边缘响应效果且连续性好。

3.2 含噪声灰度图像处理分析

为了验证双边滤波算法对噪声的抑制能力，在原始灰度图像中加入2%的椒盐噪声，同样采用2种算法进行仿真分析对比，仿真实验结果如图2所示：

图2(e)是在原始灰度图中加入椒盐噪声后的图像，图2(f)是用双边滤波算法滤除椒盐噪声，图2(g)是用传统的Canny算子处理含噪声原始灰度图，图2(h)是文中改进算法处理含噪图像，经过对比发现，图2(g)中明显含有的噪声和弱边缘信息较多，且边缘连接性差，图2(g)中对噪声的滤除效果较好，保留的边缘信息更多且连续性也更好。

4 结论

针对传统Canny边缘检测算法在进行轮对踏面损伤处理时存在的缺陷，提出一种改进的Canny算法对踏面损伤区域进行边缘检测。文中创新点有：(1）改进的算法采用双边滤波算法代替传统的高斯滤波对图像滤波去噪，对噪声具有较好的抑制能力；(2)在Soble算子基础上加入45°和135°方向计算梯度幅值，使踏面边缘细节更加清晰；(3）使用Otsu法自适应的确定高低阈值，从而避免人为设定高低阈值的缺陷，增强了自适应性。

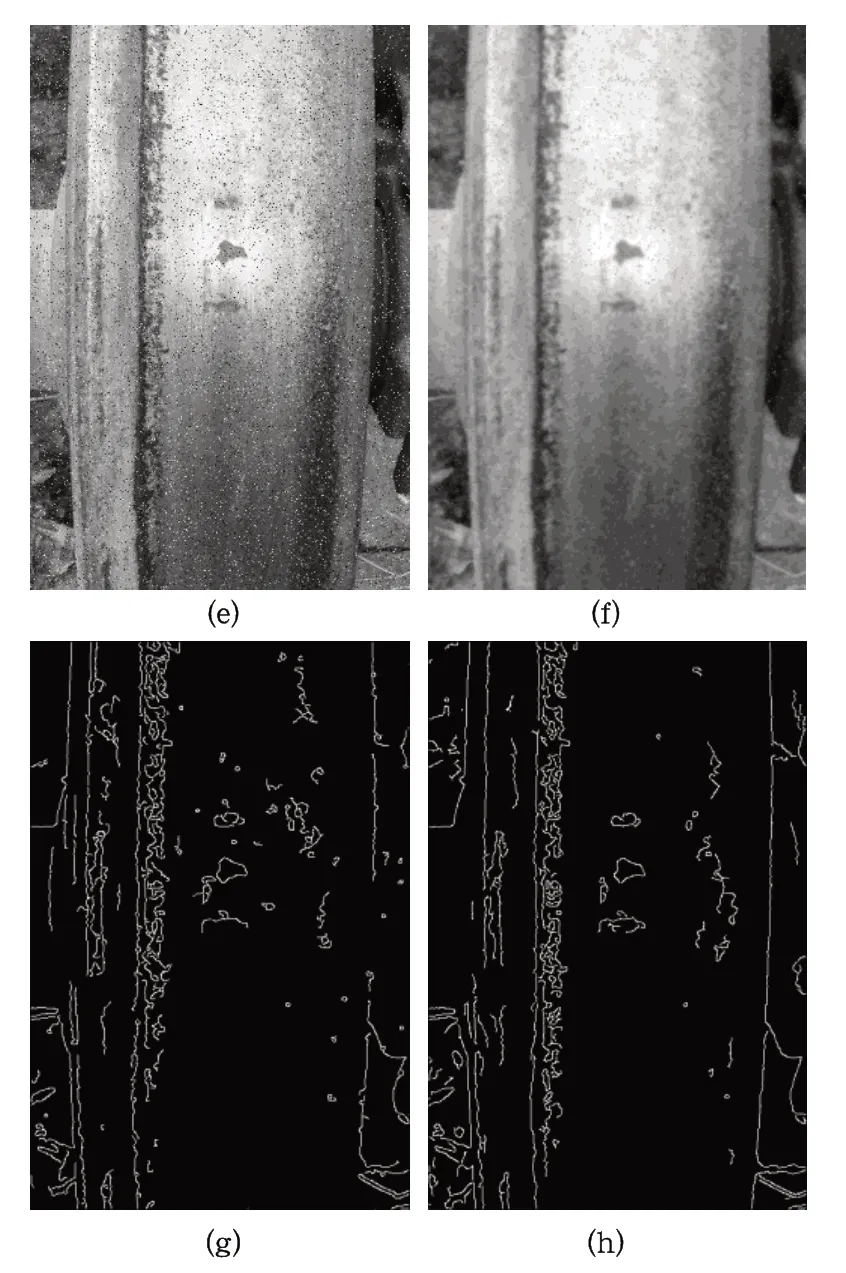
图2 含噪图像仿真实验结果