一种货运列车节能优化方法研究*

柴 杨，刘 成，王青元，白宝雪，张桂南

（1 西南交通大学 电气工程学院，成都 611756；2 中国铁道科学研究院集团有限公司 机车车辆研究所，北京 100081）

随着我国铁路运输规模的不断扩大，如何削减铁路系统的能源消耗成为重要问题。因此，研究如何实现货运列车的节能运行，对降低铁路运输成本具有关键意义。1970年，Figuera[1]提出列车在以平缓坡道为主的短途区间运行时，列车优化操纵应包括牵引、惰行以及制动3个阶段。后来，Milroy[2]以最优控制理论为基础，利用Pontrayagin极大值原理推导列车最优的操纵工况序列为全力牵引、惰行和最大制动3种不同的工况组合而成。丁勇[3]提出了基于目标速度的列车控制策略，改善了定时约束下的列车节能操纵。王青元[4]等将再生制动与空气制动相分离，提出了考虑再生制动能量利用和牵引系统效率的高速列车节能最优操纵优化算法。Lee[5]发现在长距离运行时，还会存在区间恒速工况。Liu R F[6]发现在准点和限速约束下，还存在部分制动工况，并讨论了5种最优工况的切换时机。

基于极值原理推导，以伴随变量寻优间接求解列车节能最优控制问题，优势在于，解释了有限种操纵工况的最优性及应用时机，这与优秀司机操纵经验高度一致。但基于极大值原理的速度轨迹最优化间接求解法涉及大量的微分计算及迭代求解，算法复杂，且计算量较大[7]。因此，一类数学规划方法被应用到列车运行优化控制，其特点在于将最优控制问题转化为数学规划问题进行求解，可避免复杂的理论推导，计算量在一定程度上可根据求解精度需求进行调整。荷兰代尔夫特理工大学的Wang Y[8-9]等将高斯伪谱法、混合整数规划等方法引入列车节能优化操纵中，并应用于地铁线路。唐海川[10]将列车车速离散化，将线路划分成子区间，应用动态规划算法进行在线求解。Zhang[11]以减小货运列车车钩间作用力、牵引能耗、提高速度跟踪性能为目标，将列车节能优化问题转化为二次规划问题进行求解。但这类数学规划方法在最底层寻优往往采用非线性规划，其空间离散求解的本质决定了其无法得到恒速区段的奇异控制工况，取而代之的是一定速度波动下的准恒速控制。此外，上述研究都忽略了电分相存在时不可使用牵引工况的实际工程应用情况。

尝试将最优控制理论得到的有限工况集及奇异控制工况应用优势，与数学规划求解高效灵活的特点相结合，同时考虑电气化铁路电分相对操纵工况的影响，提出了一种基于极大值原理分析结论的动态规划算法，在保证求解精度的同时实现快速优化，可有效降低列车运行能耗，实现全局意义的节能运行优化。

1 问题描述与建模

1.1 列车节能运行优化问题

列车节能运行优化问题可以做如下描述：

对于给的列车车型与列车运行线路，列车由静止出发，在所给运行时间的约束下到达终点站并停车。在满足列车安全、平稳运行的前提下，建立列车节能优化操纵模型，采用特定求解算法进行优化、计算求解，给出列车操纵策略，保证列车运行能耗最少。

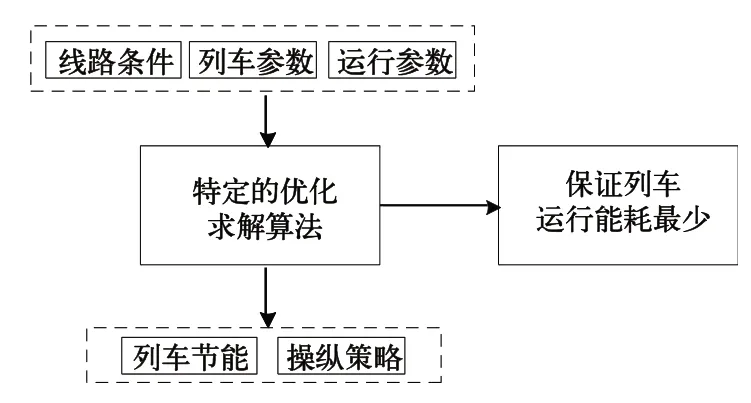
图1 列车节能运行优化框图

1.2 列车节能运行优化模型

列车节能运行优化模型的目标函数为：

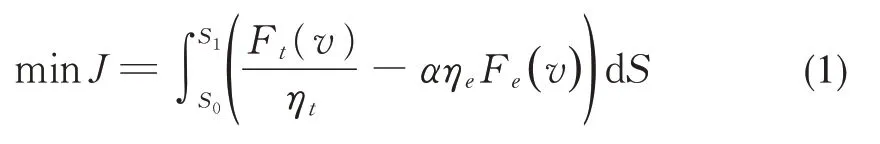
式中：S0为运行区间起点位置；S1为运行区间终点位置；Ft为列车所发挥的牵引力；Fe为列车发挥的电制动力；ηt、ηe分别对应于列车牵引、电制动工况下的整车机电效率的等效值；α为列车再生制动能量利用率。

列车运行速度应满足：

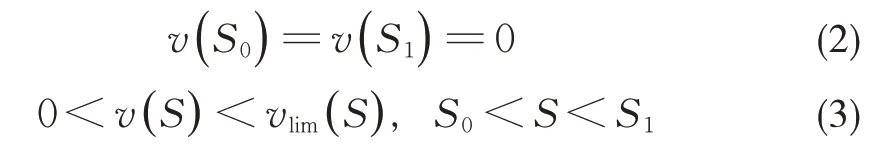
式(2)为列车在起车点与停车点的关键点约束；式(3)中，vlim表示列车的限速。

列车运行时分应满足：

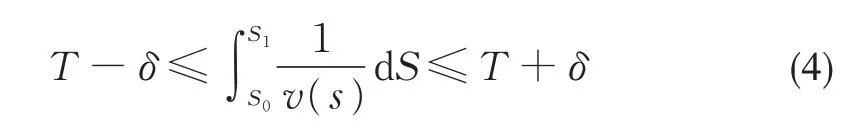
式中：T为区间的计划总运行时分；v(S)为位置S处的速度；δ为最大允许时分偏差，δ＞0。

列车的运动方程如下：

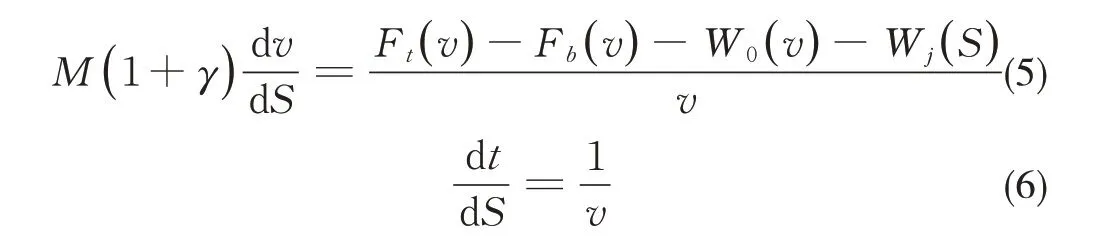
式中：M为列车质量；γ为列车回转质量系数；Fb为列车所受总制动力；W0为列车所受基本运行阻力；Wj为列车所受线路附加阻力。

列车受力应满足：

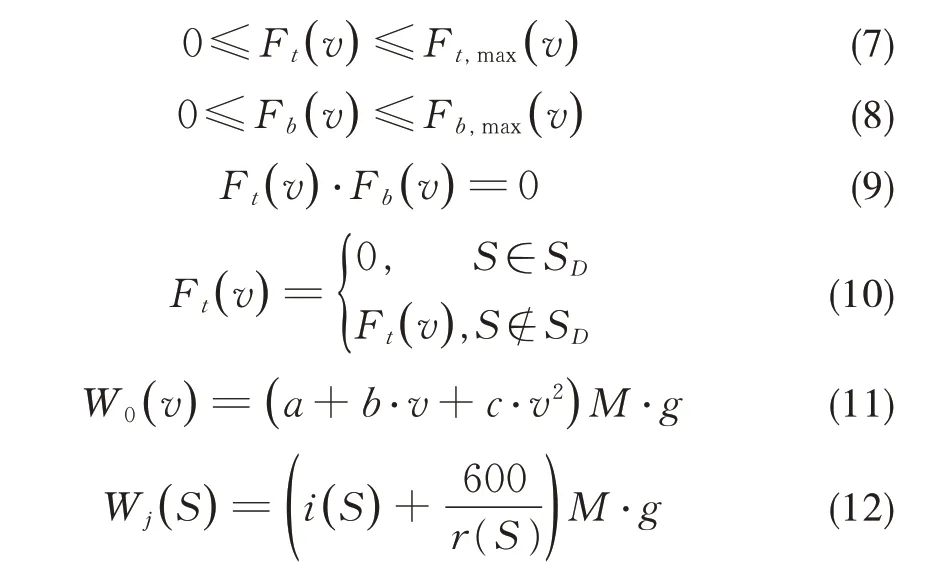
式中：Ft，max、Fb，max分别为当前运行速度下能施加的最大牵引力、制动力；SD为电分相区域集合；g为重力加速度，a、b、c为基本阻力系数，r为线路曲线半径i(x)为坡度千分数。

列车节能运行优化模型可由式(1)～式(12)建立。

2 动态规划求解

2.1 列车节能运行优化理论

根据极大值原理的分析结论，要使列车在规定时间内的区间运行能耗最小，列车的运行操纵方式应由最大牵引、恒速、惰行和最大制动4种工况组成[2]。对于简单线路，典型的列车节能最优操纵过程如图2所示：

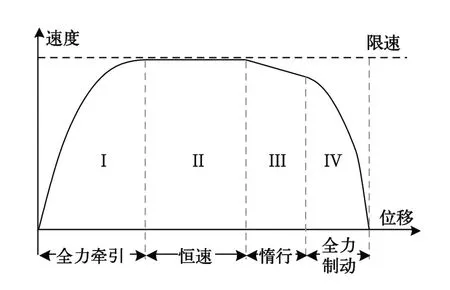
图2 典型列车节能最优操纵方式示意图

2.2 动态规划求解算法设计

文中的优化方法基于列车节能操纵的基本原理，利用列车动力学模型，设定列车恒速工况的速度间隔实现离散化，这种正向推导的方法与其他动态规划方法相比，状态生成数量要大大减少，状态空间更符合实际情况，从而使得算法计算量减少，有利于快速求解。做出定义如下：

(1) 状态：用列车所处的位置以及运行速度表示，记为G(s，v)；

(2) 决策变量：列车下一步可采取的操纵工况，记为u，u∈{u1，u2…，un}；

(3) 状态转移：由当前状态确定下一状态的过程。取决因素为决策变量，记为Gq=f(Gp，ui)，列车行驶方向正向为状态转移的方向；

(4) 状态转移成本：列车在一个状态转移或相连的若干状态转移中所付出的成本由能耗E、时间消耗T构成，记为D=E+λT，其中λ为权重系数；

(5)状态空间：所有列车状态所构成的全部集合；

(6) 状态转移路线：使列车由初状态到末状态的状态转移的集合。

综上，在求解列车的节能最优操纵方式时，需要确定列车可能到达的状态。然后求解使状态转移成本最小的状态转移路线，得到最优决策变量集合，即成本最小的操纵方式。

文中的优化算法可以通过不断调整能耗、时间的权重系数进行迭代计算，最终使最优操纵方式在时间成本满足总运行时间约束前提下实现成本最小，即为在给定时间约束下的列车操纵方式。

2.2.1确定全部状态空间

建立以位置为横轴，以速度为纵轴的直角坐标系，状态可用坐标系中的点（位置，速度）表示，其中，原点表示列车在始发站的状态。定义单位速度Δv，令列车只能以Δv的整数倍速度作为恒速运行时的巡航速度，即允许巡航速度集为vCR，其中：

考虑到实际列车具有一定长度，将线路限速以位置-速度关系绘于坐标系中。其中，在线路限速上升处，为保证列车车尾不超过限速，在列车车尾驶离低限速区段时才允许加速运行，故对限速上升处进行预处理，将低限速区向列车行驶方向延长L，如图3所示。

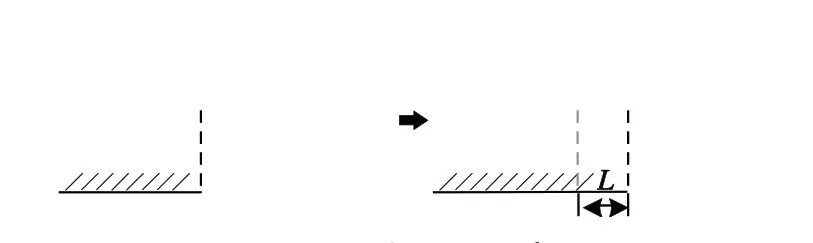
图3 限速处理示意图

在本算法的动态规划状态空间确定的过程中，引入了最优操纵优化的结论，定义了单位速度为Δv，以Δv为依据，按照其整数倍划分网格，将其作为巡航速度，绘制列车恒速曲线，从起车以及限速升高位置正向绘制全力牵引曲线，从停车以及限速降低位置反向绘制全力制动曲线。在绘制完成后，以列车的制动曲线为基础，按照Δv的间隔，反向绘制列车惰行曲线。所有曲线绘制完毕后，分别代表了4种不同的操纵工况，全线曲线之交点作为动态规划算法的状态点，所有的状态点构成了状态空间。若线路存在电分相，电分相区域内牵引曲线将被删除，从电分相始端的牵引曲线处向电分相末端绘制惰行曲线，再从惰行曲线末端绘制牵引曲线，如图4中第2区间所示；若电分相区域存在制动曲线，则无需处理，如图4中第3区间所示；其他情况则在电分相起止端的惰行曲线处向电分相两侧添加牵引曲线，如图4中第1区间所示。

求得状态空间后，两相邻状态间的曲线唯一确定一个状态转移过程，根据能耗计算公式以及列车运动方程式(6)、式(7)求得对应状态转移成本。能耗计算公式如式（13）：

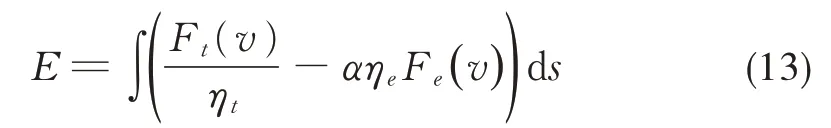
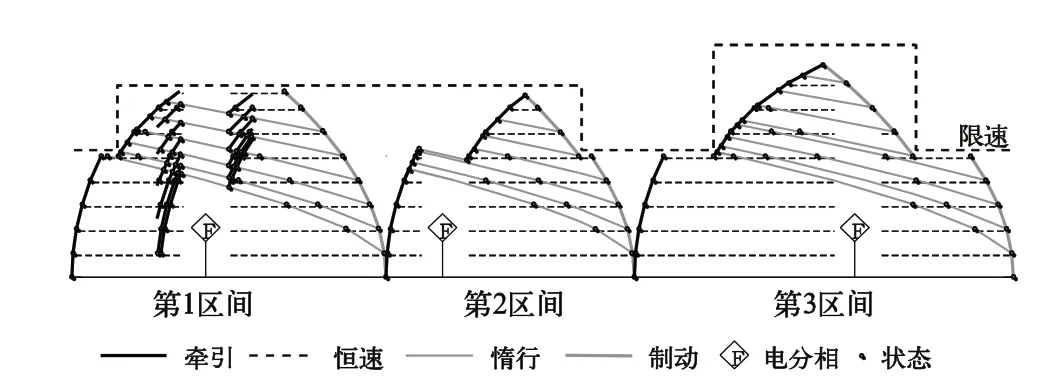
图4 状态空间求解示意图

2.2.2建立动态规划递推函数

动态规划优化目标使总状态转移成本最小，即：

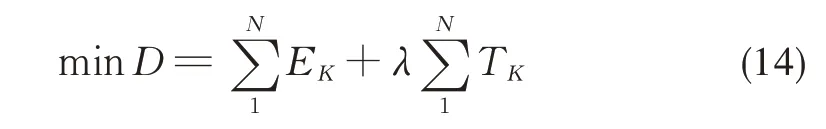
式中：EK、TK分别为某个状态转移过程中的能耗与时间成本，N对应状态转移路线中初状态到末状态之间状态转移总次数，每一个状态转移路线都对应一个确定的N值。

定义从状态转移到第p状态点的最小能耗-时间成本表示为Dp，则：

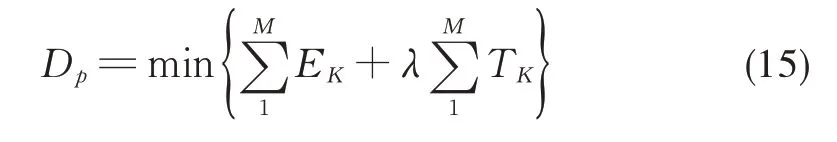
式中：M为状态转移路线中由列车初状态到某一p状态之间状态转移总次数。

从p状态到q状态的状态转移对应的状态转移成本记为：

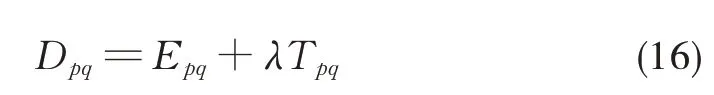
式中：Epq、Tpq分别为p状态点到q状态点状态转移的能耗与时间成本。

则最小状态转移成本的递推关系：

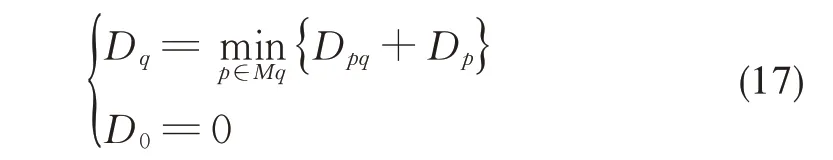
式中：Mq为所有能够通过一次状态转移到q的状态点的集合；D0为初状态点对应的最小状态转移成本。

3 仿真案例

为验证文中所构建的货运列车优化算法的有效性，在MATLAB环境下进行优化算法仿真。为使仿真尽量贴近应用实际，本节选用目前朔黄铁路实际运行的HXD1型电力机车牵引的货运列车进行仿真，仿真所用车辆为C80型货运车辆，机车、车辆和编组信息分别如表1～表3所示。

表1 HXD1型机车参数

表2 C80型货车参数

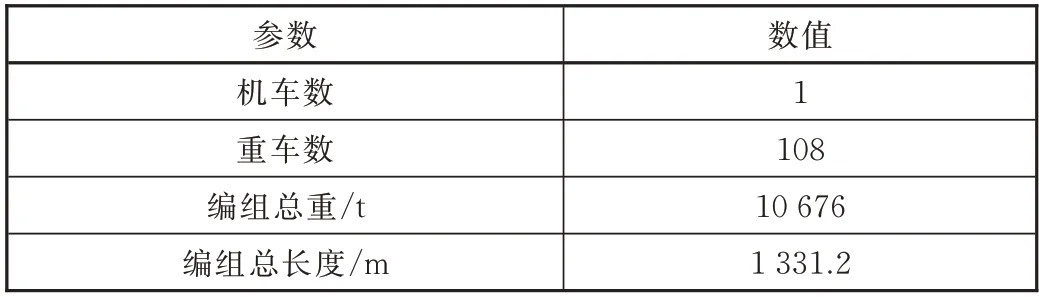
表3 编组数据

HXD1电力机车牵引控制手柄的最大级位为13级，级间可平滑调节，轴重25 t时的牵引特性如式18所示。

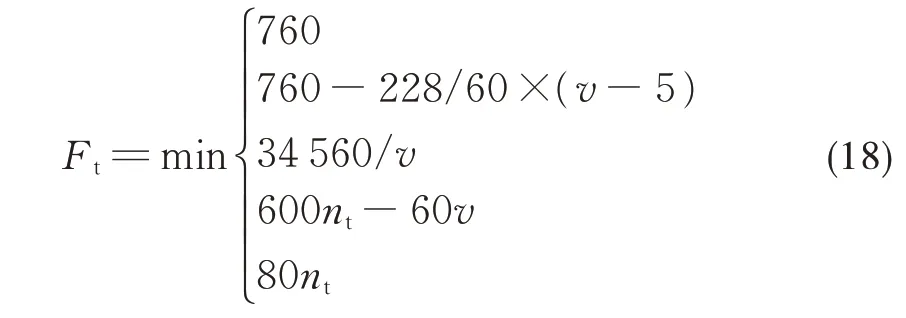
HXD1型电力机车的动力制动为再生制动，司机控制器最大手柄级位为12级，级间可平滑调节。当列车运行在复杂线路上时，司机可根据制动力需求调节机车动力制动力，实现列车调速运行。轴重为25 t时，HXD1型电力机车的再生电制动特性公式如式19所示。

采用的仿真线路是有代表性的朔黄铁路中西柏坡至肃宁北区段，运行区段线路全长165.271 km，设定时刻表规定的运行时间为9 577 s。同时，设定速度间隔为5 km/h、最低恒速速度为20 km/h，文中所述的动态规划算法所形成的状态空间如图5所示。其中：蓝色惰行曲线由制动曲线和恒速曲线的交点反向计算惰行而得出。

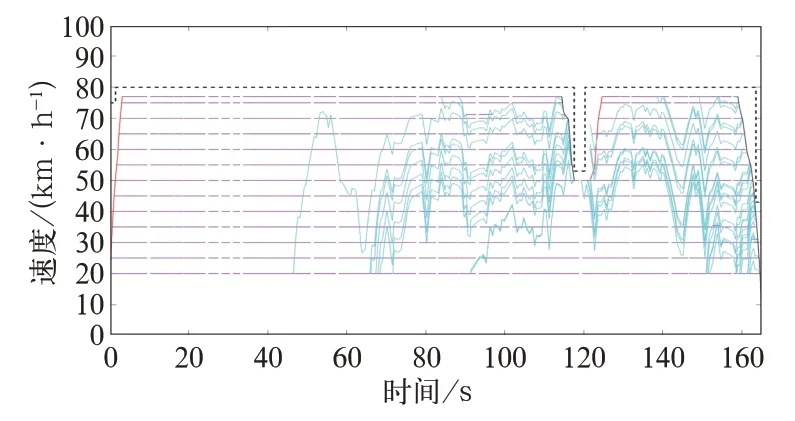
图5 列车全部状态空间

在上述仿真条件下，将实际运行时间作为计划总运行时间，根据仿真结果，列车运行速度距离曲线如图6所示。其中，红色曲线为牵引工况，紫色曲线代表恒速工况，蓝色曲线代表惰行工况，黑色曲线代表制动工况。仿真相关结果参数如表4所示。

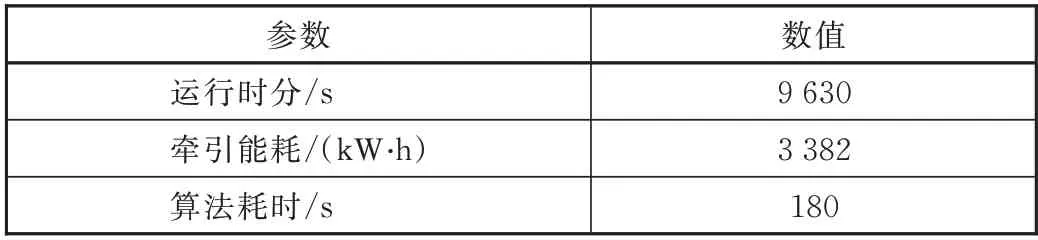
表4 列车运行时间与能耗对比

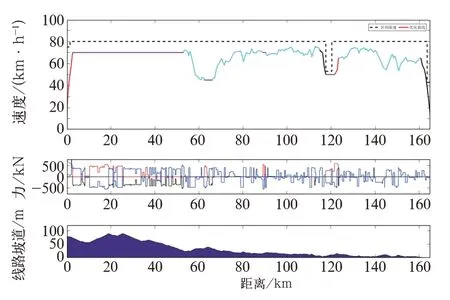
图6 列车运行速度距离曲线

分析图6中的优化所得曲线，可以发现其运行方式与最优操纵理论完全相符，起车后在安全平稳限制下全力加速运行，避免了提前惰行，使列车有更多富裕时间在制动停车前实现长距离惰行，达到节能的目的。如在K67之后，列车充分利用前方线路为长距离下坡道的优势，采用了长时间的惰行工况。直到前方出现低限速，进行调速制动。通过低限速后，在考虑列车长度，保证车尾不超限速的情况下，采用全力牵引工况，使列车更早到达较高运行速度。在达到较高的速度水平后，再利用前方以下坡为主的起伏坡道，惰行节能。直至K161处，进行停车制动。

因此，优化结果在经过大下坡道前保持较低的入坡速度，从而在进入大下坡道时通过惰行，充分利用势能使列车加速。而实车运行时由于入坡速度较大，使列车在大上坡道运行时需要通过制动让列车不超速，造成一定能量浪费。

最后，取不同的单位速度Δv进行优化并进行结果的对比，对比结果如表5所示。当Δv为2.5 km/h时，本算法耗时为463 s，计算时间较长，但牵引能耗最低。随着Δv的不断增大，算法耗时逐减小，但优化结果的牵引能耗也在增大。因此，若设定较大的单位速度Δv，计算时间大大减少，同时保证了一定的节能效果。本算法具有一定的灵活性，通过设定合适的单位速度，可以在节能效果与算法耗时上达到一个平衡，以满足工程上的不同需求。

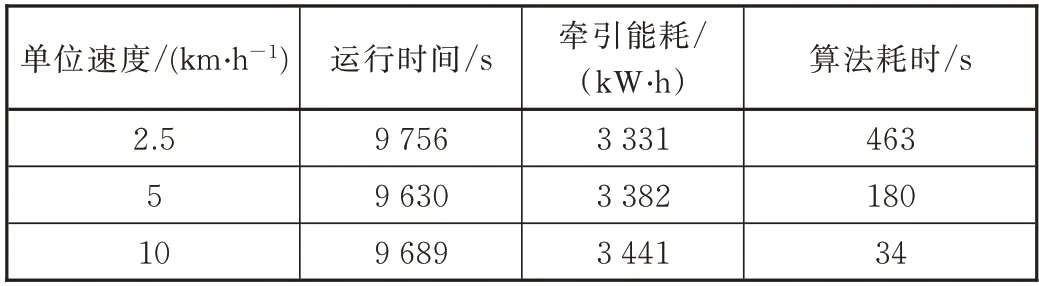
表5 不同单位速度下的优化结果对比

4 结论

设计了货运列车优化操纵算法，并在MATLAB环境下对算法进行了一系列的验证。

（1）设计了一种基于节能最优控制规则结论的货运列车动态规划算法，在保证列车总运行时间不变情况下，实现了全线的最优节能运行操纵策略优化。同时，考虑电分相情况，使本优化方法较好的应用于存在电分相的电气化铁路。

（2）以HXD1型电力机车牵引的货运列车为仿真车型，以朔黄铁路西柏坡至肃宁北区段作为仿真线路，结果显示本算法具有较好的节能性与适用性。

（3）仅在MATLAB环境下对算法进行了验证，但是为了将算法用于货运列车辅助驾驶乃至自动驾驶系统等工程环境中，需进行算法的移植与工程应用优化。